双馈风机(永磁同步风机)虚拟惯性控制+下垂控制参与系统一次调频的Matlab/Simulink模型,调频结束后转速回复,造成频率二次跌落SFD。 系统为三机九节点模型(可更换为四机两区域,十机39节点,IEEE39节点,IEEE11节点),所有参数已调好且可调,可直接运行,风电渗透率可调 风机采用虚拟惯性+下垂控制,含有转速回复模块,在系统频率跌落时释放转子动能提供有功支撑,参与电网的一次调频,在调频过程结束后,仿真时间30s时风机切换至mppt控制(退出时间可任意调节),功率骤降导致频率的二次跌落,
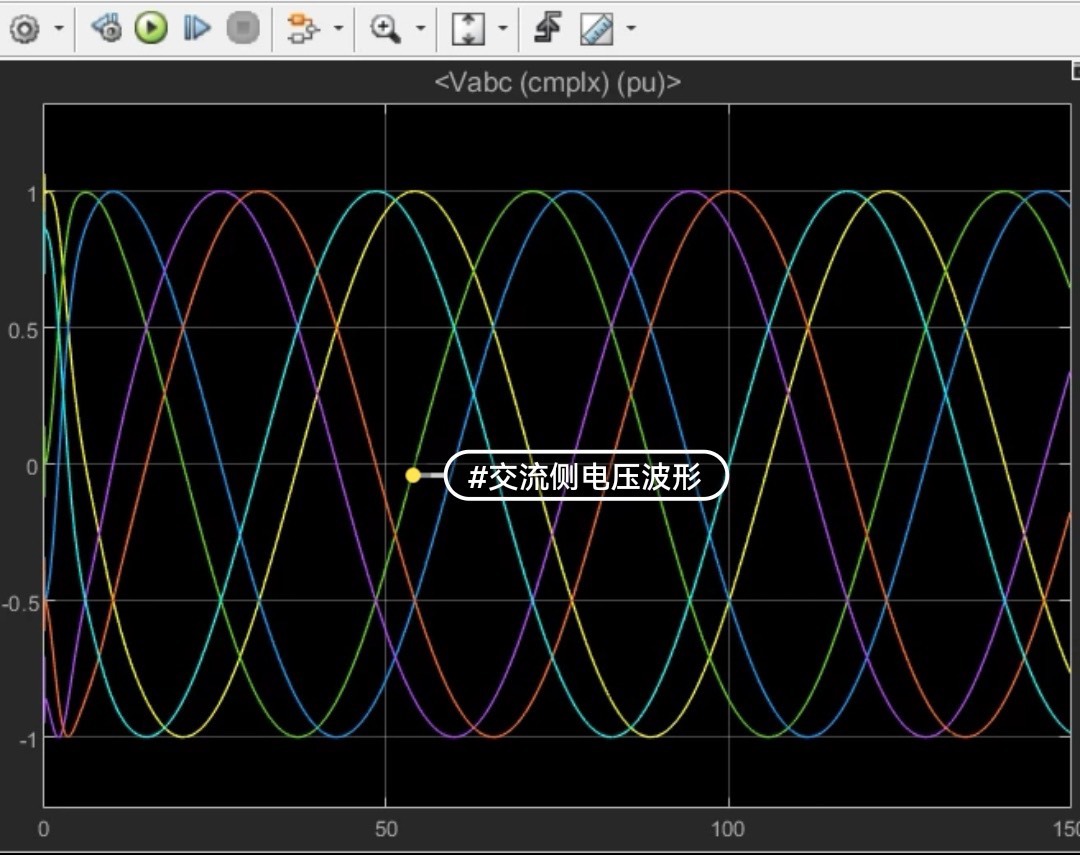
在电力系统研究领域,双馈风机(永磁同步风机)通过虚拟惯性控制和下垂控制参与系统一次调频是一个热门话题。今天咱就唠唠与之相关的Matlab/Simulink模型,以及其中出现的频率二次跌落(SFD)现象。

咱搭建的系统是三机九节点模型,当然,你要是乐意,也能换成四机两区域、十机39节点、IEEE39节点或者IEEE11节点这些常见模型。而且啊,所有参数都已经精心调好,还支持随时调整,直接运行就成。风电渗透率也是可以调节的,相当灵活。
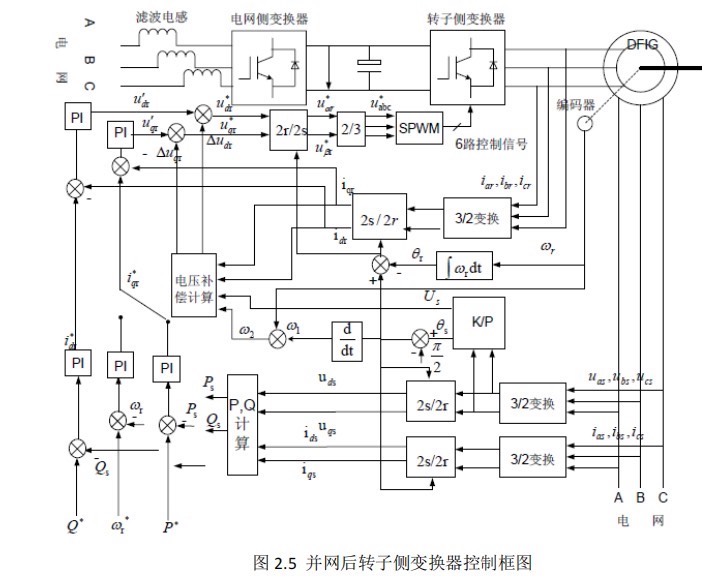
风机采用的是虚拟惯性加上下垂控制的策略,还配备了转速回复模块。这啥意思呢?当系统频率跌落的时候,风机就像个小能手,通过释放转子动能来提供有功支撑,积极参与电网的一次调频。
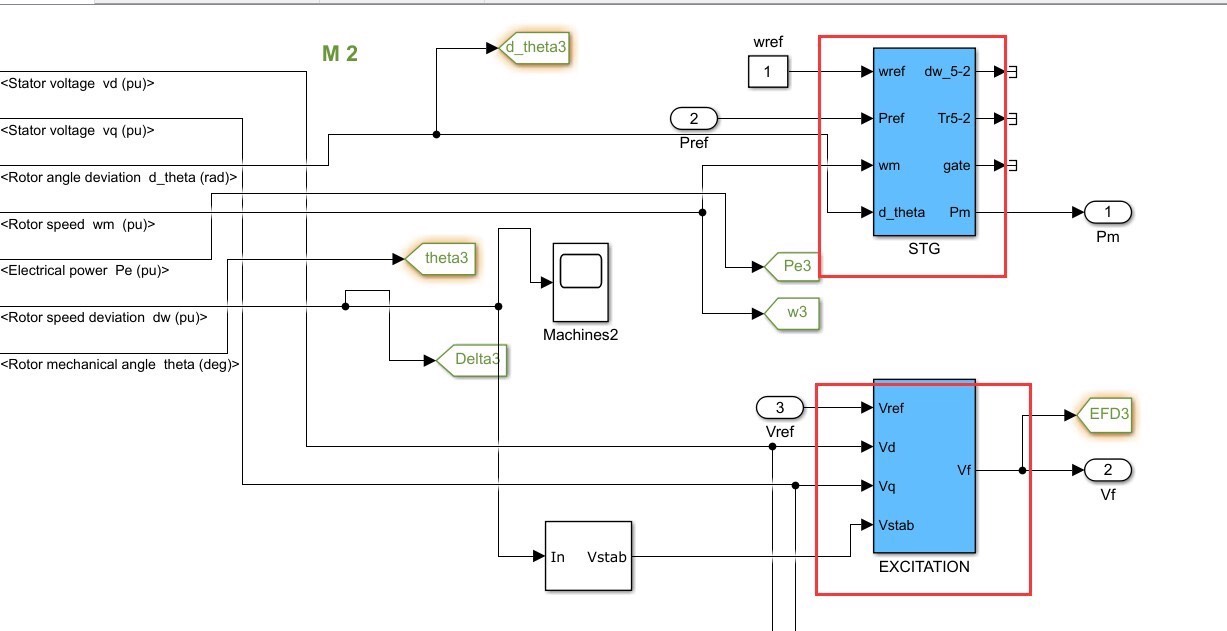
咱来看看相关代码片段(这里以简单示意代码为例,实际模型会更复杂):
matlab
% 虚拟惯性控制部分
function [P_inertia] = inertia_control(omega, omega0, D)
% omega 当前转速
% omega0 额定转速
% D 虚拟惯性系数
P_inertia = D * (omega - omega0);
end
% 下垂控制部分
function [P_droop] = droop_control(f, f0, R)
% f 当前频率
% f0 额定频率
% R 下垂系数
P_droop = (f0 - f) / R;
end在虚拟惯性控制代码里,inertiacontrol**函数根据当前转速 omega 和额定转速 omega0 的差值,乘以虚拟惯性系数 D,来算出虚拟惯性提供的功率 P inertia。下垂控制的 droopcontrol**函数则是依据当前频率 f 和额定频率 f0 的差值,除以下垂系数 R,得到下垂控制贡献的功率 P droop。
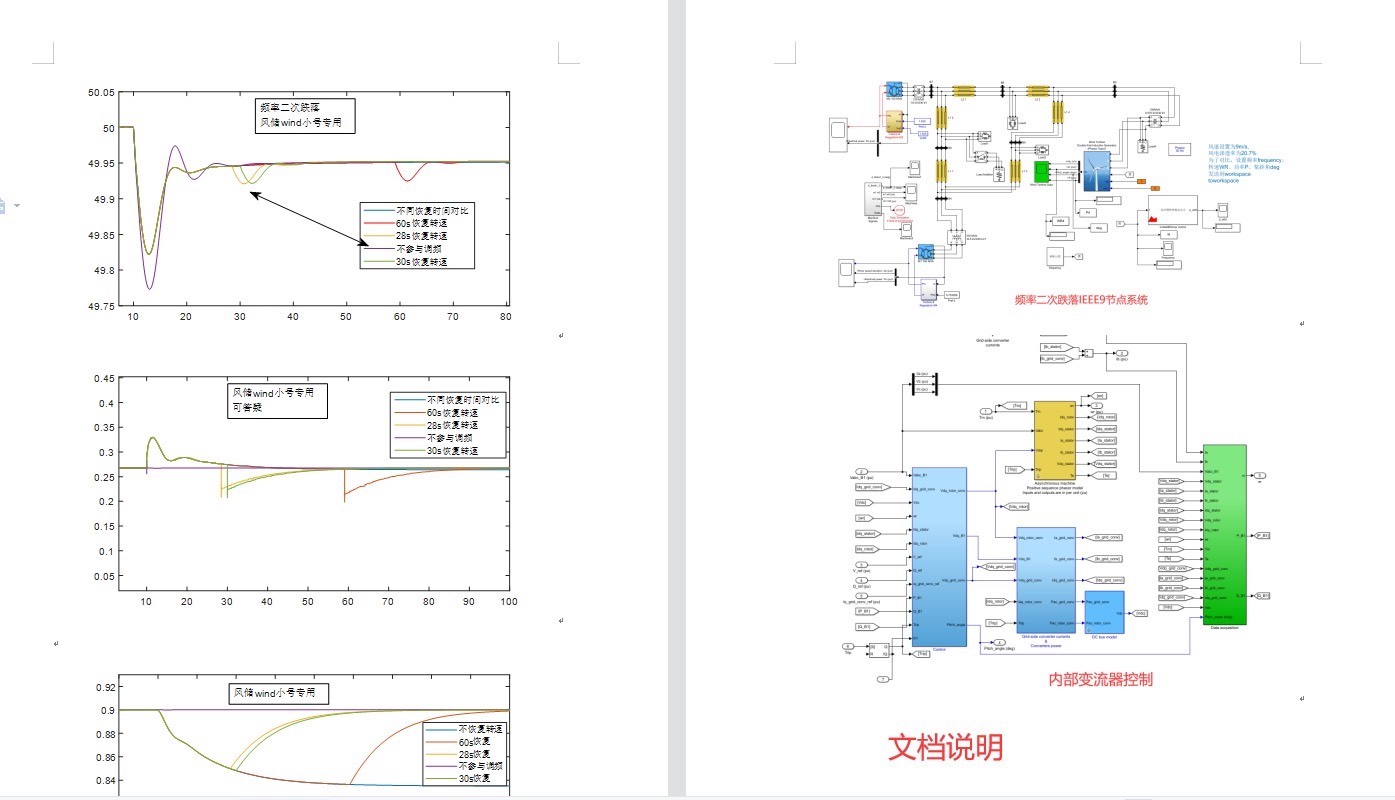
重点来了,在调频过程结束后,也就是仿真时间到30s的时候(这个退出时间可以根据实际需求任意调节哈),风机就切换到最大功率点跟踪(MPPT)控制。这一切换可不得了,功率会骤降,进而导致频率出现二次跌落。
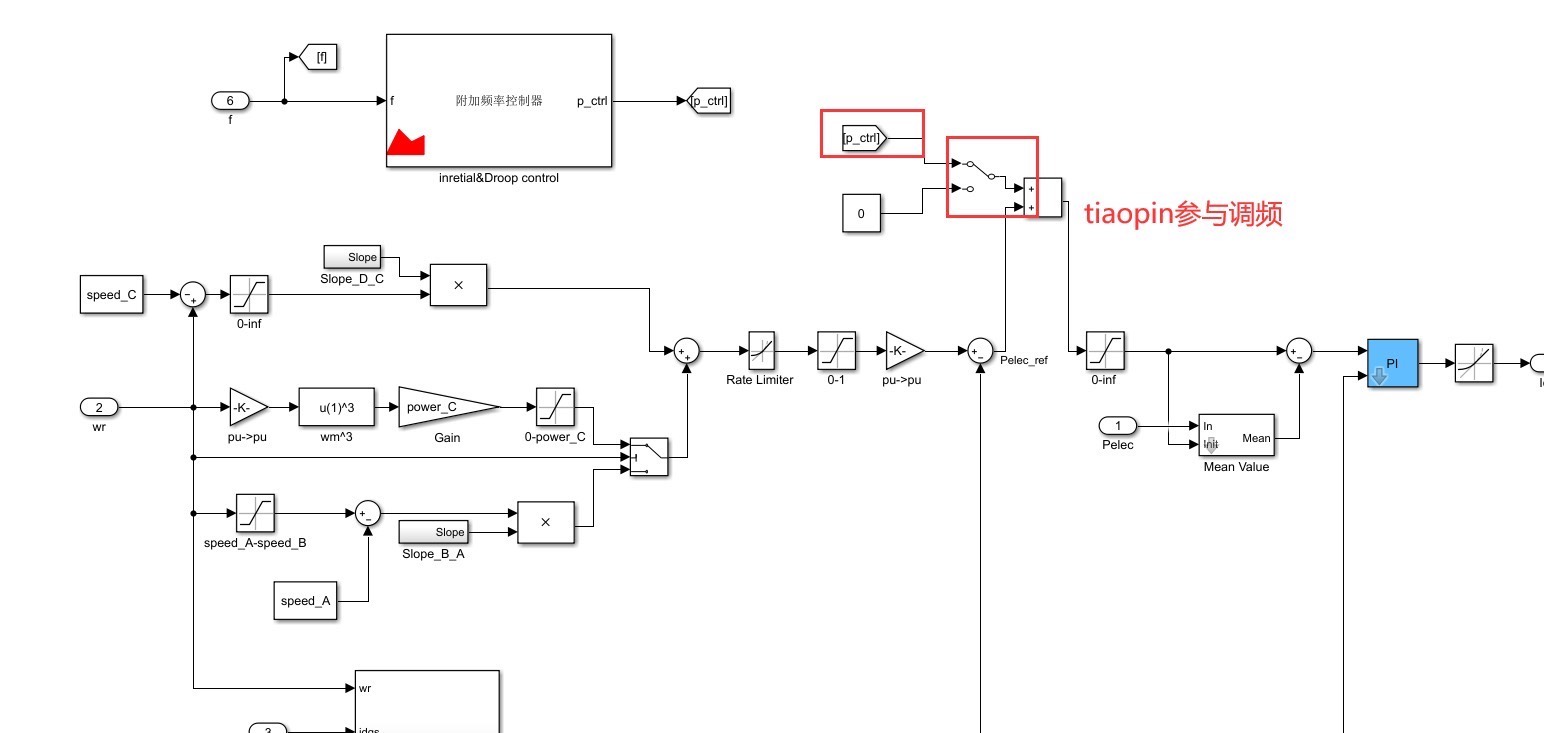
从实际模型运行来看,风机在一次调频时确实有效地利用虚拟惯性和下垂控制,对频率跌落起到了很好的抑制作用。但是当切换到MPPT控制时,由于功率的突然变化,就像平静湖面突然被投入一颗巨石,频率瞬间产生了二次跌落。
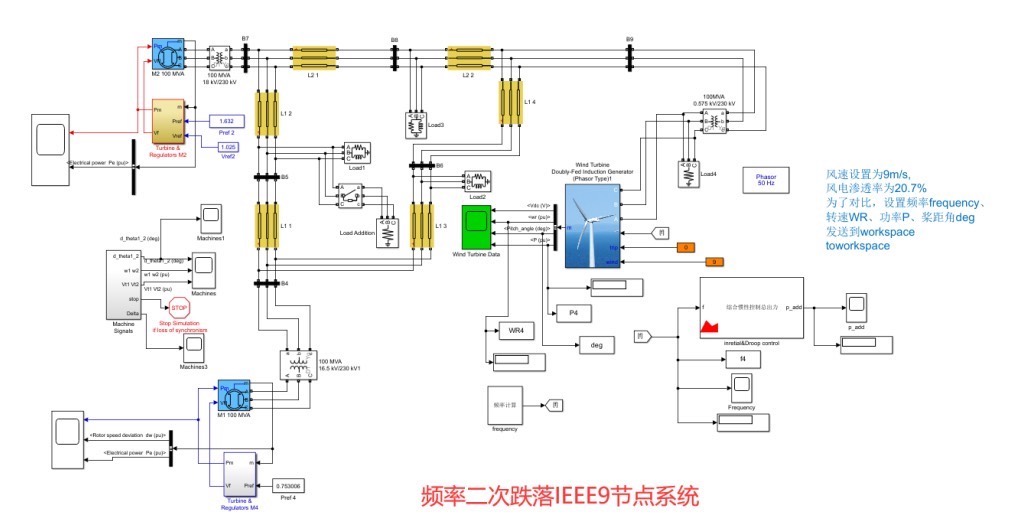
这种频率二次跌落现象在实际电力系统运行中可不能忽视,它可能会对电网的稳定性造成潜在威胁。所以我们得进一步研究怎么优化风机的控制策略,尽量减少这种二次跌落带来的不良影响,保障电网能持续、稳定地运行。
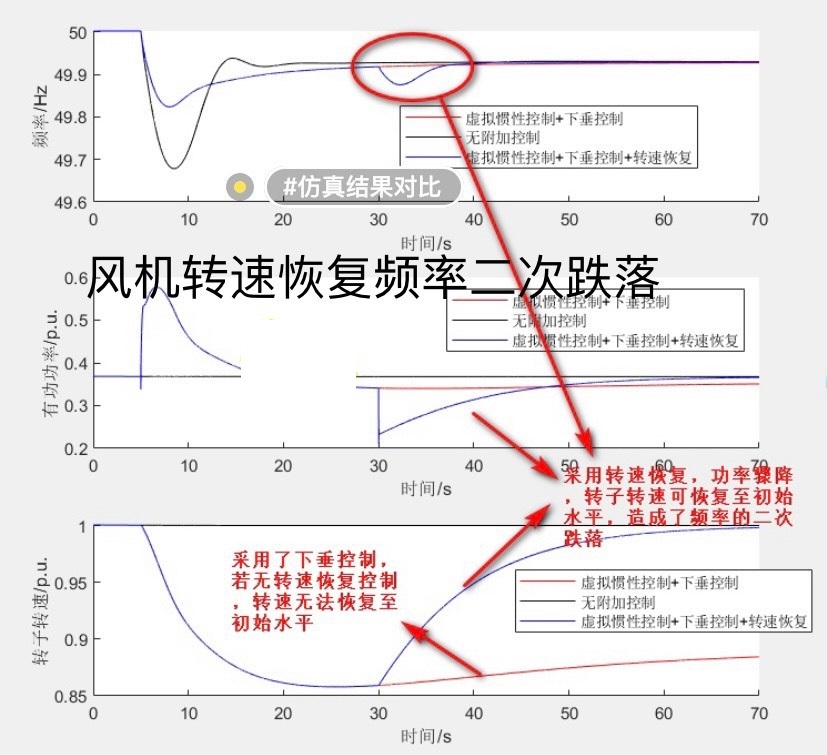
希望通过今天分享的这个Matlab/Simulink模型以及频率二次跌落现象的探讨,能给各位在电力系统研究上带来一些启发,大家一起交流进步呀。