1.证明结构
假定存在一个敌手A\mathcal AA在相关安全模型下可以打破现有的签名方案。
我们构造一个模拟器B\mathcal BB去打破一个计算困难问题。
在安全模型下首先给出困难问题的输入实例,我们必须展示
- 模拟器如何产生模拟方案;
- 模拟器如何使用敌手的攻击来解决底层困难问题;
- 安全规约为什么是正确的;
一个安全证明必须包含以下三部分:
- 模拟。需要展示模拟器如何使用问题实例去产生一个模拟方案,以及如何与敌手在不可伪造模型下进行交互。如果模拟器不得不中断,安全规约失败。
- 解决办法。需要展示模拟器如何使用敌手产生的伪造签名来解决底层困难问题。简单来说,模拟器应该能够从伪造签名中提取到一个问题实例的解。
- 分析 。需要展示以下分析
(1).模拟与真实攻击对敌手而言是不可区分的。
(2).成功模拟的概率PSP_SPS。
(3).有效模拟的概率PUP_UPU。
(4).求解底层困难问题的优势 εR\varepsilon_RεR。
(5).解决底层困难问题的时间开销。
如果模拟器在计算公钥和回应敌手问询时没有发生中断,那么模拟就是成功的。
如果所有被计算的签名都可以通过签名认证,且模拟过程具有随机特性,那么这个模拟过程就是不可区分的。如果模拟器能够从伪造签名中提取到一个问题实例的解,那么敌手的攻击就是有效的。
许多安全证明仅仅计算成功模拟的概率,而不计算有效攻击的概率。这种分析与我们的方法一致,因为其定义中的成功模拟概率已包含攻击的有效性。差异源于对成功模拟的不同定义。
针对数字签名的安全规约,不必利用伪造的签名来解决数学困难问题。在随机预言机模型下,模拟器可以使用哈希问询,取代使用伪造签名解决数学困难问题。
2.计算优势
让ε\varepsilonε表示敌手打破所提签名方案的优势。
敌手解决一个底层困难问题的优势用εR\varepsilon_RεR表示,那么
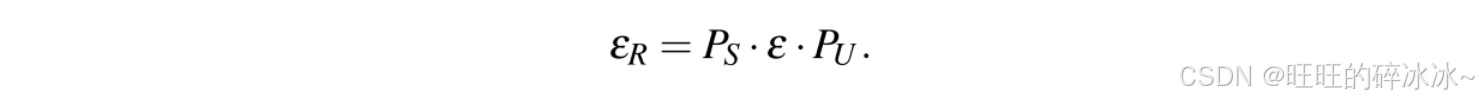
若模拟成功且以概率 PSP_SPS与真实攻击无法区分,则敌手能以概率 ε\varepsilonε成功伪造有效签名。
以概率 PUP_UPU计算,伪造签名构成有效攻击,该攻击可归约为求解底层困难问题。因此,我们将 εR\varepsilon_RεR定义为安全归约中求解底层困难问题的优势概率。
3.模拟和规约
在安全性归约中,若问题实例的解可从敌手的伪造签名中提取,则可将模拟方案中的所有签名分为两类:可模拟签名与可归约签名。
- 可模拟的签名。如果一个签名可以通过模拟器进行计算,那么它就是可模拟的。如果伪造的签名是可模拟的,那么伪造攻击就是无效的。否则,模拟器可自行计算伪造签名并作为攻击者实施操作。即使没有敌手的协助,该安全归约也能成功。换言之,模拟器可独立解决底层困难问题。这种安全归约是错误的。
- 可规约的签名。如果签名可以用来解决底层困难问题,那么该签名就是可规约的。如果伪造签名是可规约的,那么攻击就是有用的。在安全规约中的规约签名不可以被模拟器计算出来。否则,模拟器可以通过它自己解决底层困难问题。
对于数字签名的安全规约,在模拟方案中的每一个签名都应该要么是可模拟的,要么是可规约的。一个成功的安全规约需要所有被问询的签名都是可模拟的,伪造的签名都是可规约的。否则,模拟器不能回应来自敌手的签名问询,或者使用伪造的签名来解决底层困难问题。
4.私钥的模拟
在数字签名的安全证明中,大多数安全证明在编写安全规约时,都是以模拟器不知道相关私钥的方式。
直觉上,如果模拟器知道了私钥,那么所有的签名都是可模拟的,包括伪造的签名。因此规约就是不成功的。但是,这个观点是不对的。可以在模拟器知道私钥的情况下编写模拟。需要强调的是,即使模拟器知道私钥,签名也必须可规约;否则,安全规约就是不正确的。这是一个在安全规约中必须要被解决的矛盾。
书中所有介绍和给定方案均将安全归约编写为模拟器无法获知密钥的形式。也就是说,在此类模拟中,若模拟器知晓密钥,便能立即解决底层困难问题。
5.partition
在规约中,模拟器必须向敌手隐藏哪个签名是可模拟的,哪个签名是可规约的。
如果敌手总是可以返回一个模拟的签名作为一个伪造签名,这个规约对于解决底层困难问题没有优势。
我们将签名划分为上述两个集合的方法称为partition。模拟器必须阻止知晓归约算法并能发起签名查询的敌手发现该划分。目前采用两种不同方法来处理这种partition问题。
- 寻找中的难解性。给定一个模拟,包括签名问询,计算无界的敌手不能寻找到这个partition的概率为1。因此敌手返回的伪造的签名以不可忽略的概率PUP_UPU是可以规约的。为了在安全规约中,对计算无界的敌手隐藏这个partition,模拟器应该使用完全困难问题在模拟的时候隐藏他。
- 区分中的难解性。给定包含查询签名和两个互补partition的模拟场景,计算能力无界的敌手在区分所用partition时不具备任何优势,因此敌手仅能以1/2的概率正确猜测partition。此处互补partition指:模拟中的任何签名必须能通过一个partition模拟生成,或通过另一partition归约得到。此时,敌手将以1/2的概率返回一个可归约的伪造签名。此处的秘密信息I\mathbb II为模拟过程中实际采用的partition。需注意,并非必须构造严格互补的两个partition,只要敌手无法始终找到在两个partition中均可模拟的签名即可。
在与第一种方法比较时,第二种方法并不需要隐藏敌手的partition。partition在规约算法中是固定的。为了确保在第二种方法中有两个不同的partition,必须提出两种不同的模拟算法。一个规约算法至少包含两个模拟算法和与之相关的解决算法。
紧密规约与松弛规约的回顾
回顾二者定义,有以下发现
- 如果相同消息的签名要么是可模拟的,要么是可规约的;一个随机选择的消息可模拟的概率为PPP,那么这个规约算法必须是松弛的。令qsq_sqs为签名问询的数量。如果敌手随机选择要签名的消息,成功模拟和有效攻击的概率就是Pqs(1−P)≤1qsP^{q_s} (1 - P) \leq \frac{1}{q_s}Pqs(1−P)≤qs1。该松弛规约与qsq_sqs的数量呈线性关系,因此安全规约是松弛的。
- 若消息的签名可被生成可模拟 或可归约 的形式,则能实现紧密归约。对于消息的签名查询,模拟器使其具备可模拟性。此时,对签名查询的响应不会出现中止。设 1−P1-P1−P为伪造签名可归约的概率,则成功模拟与有效攻击的概率为 1⋅(1−P)1 \cdot (1-P)1⋅(1−P),而非 Pqs(1−P)P^{q_s}(1-P)Pqs(1−P)。当 1−P1-P1−P为常数且较小时,安全归约是紧密的。
我们发现,所有具有紧密归约的现有签名方案在签名生成阶段均使用了随机盐值,该盐值用于在可模拟与可归约之间进行切换。因此,任何在签名生成过程中不含随机盐值的唯一性签名方案似乎均无法实现紧密归约。然而,借助随机预言机模型,可为特殊构造的唯一性签名方案设计紧密归约,其中底层困难问题的解来自某个哈希查询。
7.正确安全规约总结
一个数字签名方案中正确的安全规约,模拟器不知道私钥,同时应该满足以下条件,可以使用这些条件去检查一个安全规约正确与否。
- 底层困难问题是一个计算困难问题。
- 模拟器不知道私钥。
- 所有的签名问询在不知道私钥的情况下是可以模拟的。
- 模拟与真实攻击是不可区分的。
- 该partition难以处理或无法区分
- 伪造的签名是可以规约的。
- 解决底层困难问题的优势εR\varepsilon_RεR是不可忽略的。
- 模拟的时间开销是多项式时间。
当模拟器通过哈希查询解决底层困难问题或已知密钥时,安全归约的方法将发生改变。然而,由于这两种情况极为特殊,不再赘述。