周志华《机器学习---西瓜书》六
六、神经网络模型
6-1、神经网络
什么是神经网络?
- "神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应! IT.Kohonen,1988,Neural Networks 创刊号
- 神经网络是一个很大的学科领域,本课程仅讨论神经网络与机器学习的交集,即"神经网络学习"亦称"连接主义(connectionism)"学习
"简单单元"神经元模型
M-P 神经元模型 [McCulloch and Pitts,1943]
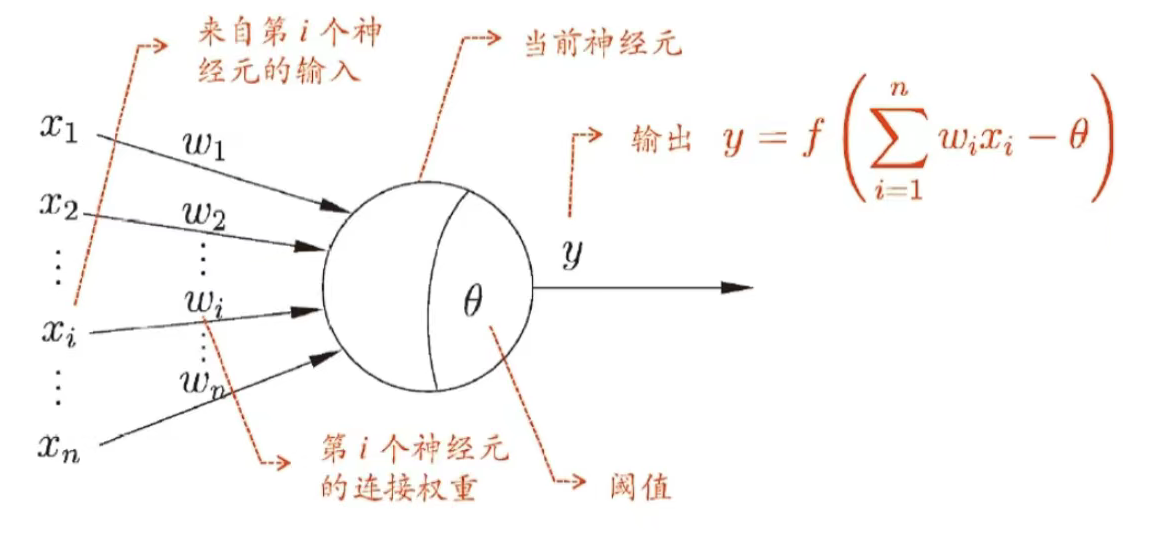
注意: 圆圈的里面的弧线是输入加权结果大于阈值的意思
神经网络学得的知识蕴含在连接权与阈值中
神经元激活函数
- 理想激活函数是阶跃函数,0表示抑制神经元,而1表示激活神经元阶
- 阶跃函数具有不连续、不光滑等不好的性质,常用的是 Siamoid函数
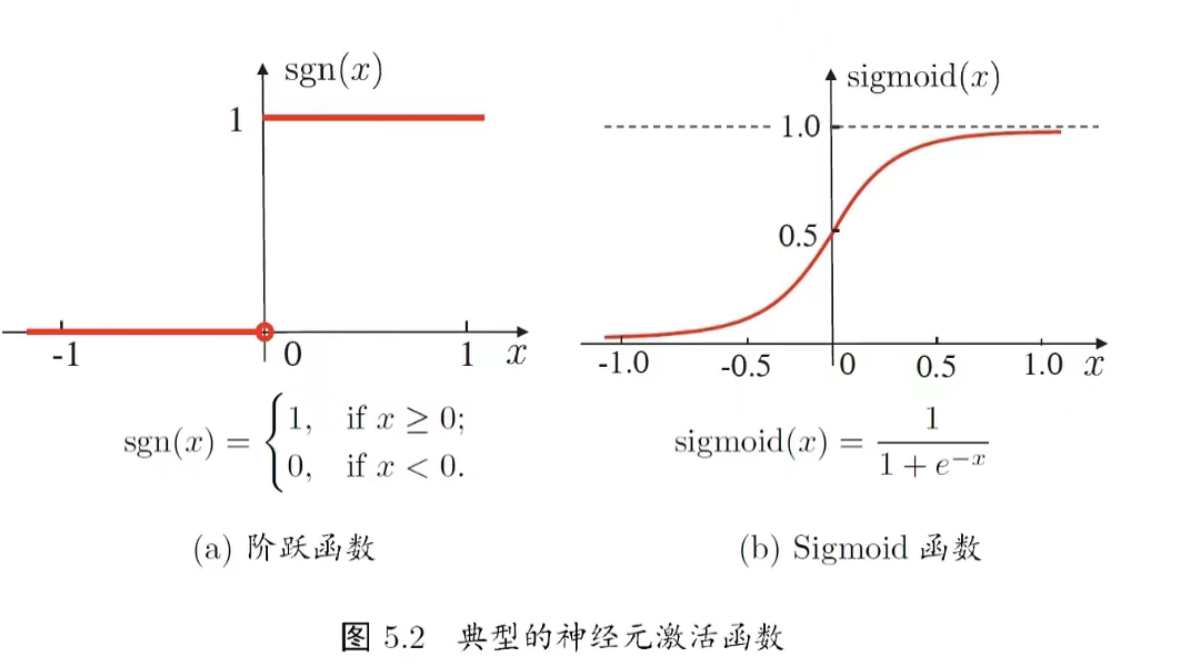
Sigmoid函数(即S型函数 sigmoid(x)=11+e−x\text{sigmoid}(x) = \frac{1}{1+e^{-x}}sigmoid(x)=1+e−x1 ) 的核心优势是连续光滑、可导,这是它替代阶跃函数的关键,具体好性质包括:
- 连续且光滑 :
阶跃函数是不连续的(在 ( x=0 ) 处突变),而Sigmoid在全体实数域上连续、处处可导,这满足了神经网络梯度下降优化的需求(梯度需要连续的函数来计算)。 - 值域在(0,1)之间 :
输出结果可以自然地被解释为"概率"(比如在二分类任务中,输出接近1表示正类,接近0表示负类),符合分类任务的概率语义。 - 导数易计算 :
其导数可以用自身表示: sigmoid′(x)=sigmoid(x)⋅(1−sigmoid(x))\text{sigmoid}'(x) = \text{sigmoid}(x) \cdot (1 - \text{sigmoid}(x))sigmoid′(x)=sigmoid(x)⋅(1−sigmoid(x)) ,计算效率高,适合神经网络的反向传播。 - 单调性 :
函数单调递增,能保持输入信号的"强弱"趋势(输入越大,输出越接近1;输入越小,输出越接近0)。
6-2、万有逼近能力
多层前馈网络结构
核心定义
- 多层网络:包含隐层的网络。
- 前馈网络:神经元之间不存在同层连接,也不存在跨层连接(信号仅从输入层→隐层→输出层单向传递)。
- 功能单元:隐层和输出层的神经元又被称为"功能单元"。
结构图示
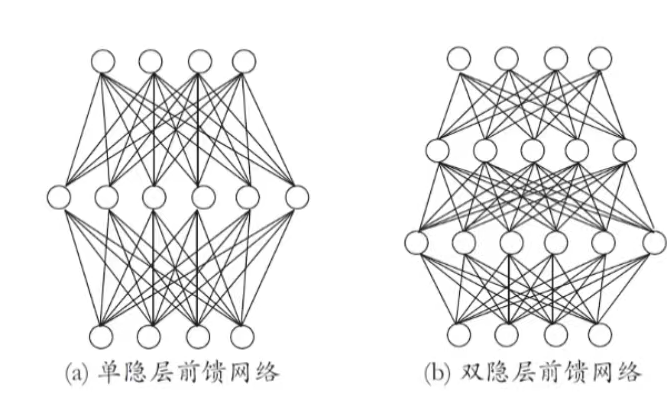
关键性质:万有逼近性
多层前馈网络有强大的表示能力 ("万有逼近性")
仅需一个包含足够多神经元的隐层 ,多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数(来源:[Hornik et al., 1989])。
待解决问题
隐层神经元的数量设置是未决问题(Open Problem),实际应用中常用"试错法"调整。
6-3、缓解过拟合
核心策略包括两种:
1. 早停(early stopping)
-
核心逻辑:通过监控训练过程,提前终止训练以避免模型过度拟合训练数据。
-
常见触发条件:
- 训练误差连续 aaa 轮的变化小于阈值 bbb ;
- 结合验证集:当训练误差持续降低,但验证误差开始升高时(说明模型已开始拟合训练集噪声),停止训练。
2. 正则化(regularization)
- 核心逻辑:在模型的误差目标函数中加入"网络复杂度惩罚项",限制模型的复杂度,避免过拟合。
- 示例公式:
E=λ1n∑k=1nEk+(1−λ)∑iwi2E = \lambda \frac{1}{n}\sum_{k=1}^{n} E_k + (1-\lambda) \sum_{i} w_i^2E=λn1∑k=1nEk+(1−λ)∑iwi2
其中:
- 1n∑k=1nEk\frac{1}{n}\sum_{k=1}^{n} E_kn1∑k=1nEk 是训练误差项;
- ∑iwi2\sum_{i} w_i^2∑iwi2 是网络复杂度惩罚项(通常是连接权值的平方和);
- λ\lambdaλ 是平衡两项的权重系数。
- (1−λ)∑iwi2(1-\lambda) \sum_{i} w_i^2(1−λ)∑iwi2 偏好较小的连接权和阈值,使网络输出更"光滑",降低对训练数据噪声的敏感性。
6-4、神经网络简史
神经网络发展回顾
-
萌芽期(1940年代)
- 1943年:M-P模型(模拟神经元的数学模型)
- 1945年:Hebb学习规则(神经元连接强度的更新规则)
-
繁荣期(1956-1969年左右)
- 1958年:感知机(首个可训练的神经网络模型)
- 1960年:Adaline(自适应线性神经元)
-
冰河期(1969年后)
- 1969年:Minsky & Papert出版《Perceptrons》,指出感知机仅能解决线性可分问题,限制了其应用,导致神经网络研究遇冷。
-
再繁荣期(1984-1997年左右)
- 1983年:Hopfield网络(递归神经网络)
- 1986年:BP算法(反向传播,解决多层网络训练问题)
-
沉寂期(1997年后)
- SVM等统计学习方法兴起,神经网络研究热度下降。
-
当前繁荣期(2012年至今)
- 深度学习兴起,成为主流研究方向。
补充:发展呈现"热十三-冷十五-热十三"的交替模式,技术瓶颈与新方法突破是阶段转换的核心原因。
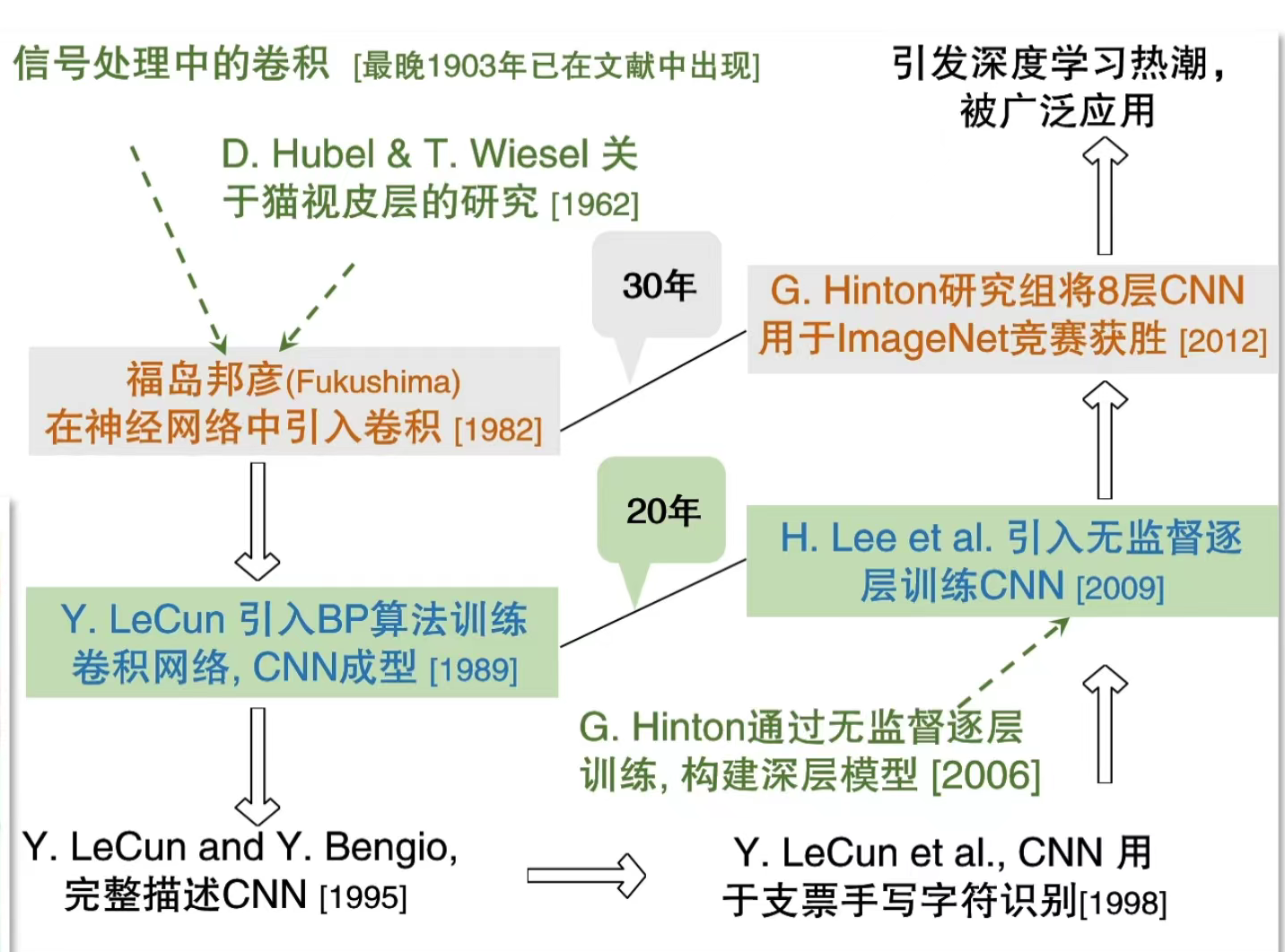
例如:CNN(卷积神经网络)
-
理论基础
- 信号处理中的卷积(1903年已出现)
- 1962年:Hubel & Wiesel发现猫视皮层的局部感受野机制(为CNN的卷积层提供生物学启发)
-
技术雏形
- 1982年:福岛邦彦在神经网络中引入卷积操作
- 1989年:Y. LeCun用BP算法训练卷积网络,CNN基本成型
- 1995年:LeCun与Bengio完整描述CNN结构
- 1998年:CNN用于支票手写字符识别(首次实用化)
-
深度学习热潮的触发
- 2006年:Hinton提出无监督逐层训练,解决深层模型训练难题
- 2009年:H. Lee等用无监督逐层训练优化CNN
- 2012年:Hinton研究组的8层CNN在ImageNet竞赛中获胜,引发深度学习广泛应用。
总结
坚持!!!

