基于无人船的smith-pid跟踪控制资料。 首先,针对pid进行了改进,有传统pid,最优pid和基于smith的pid三种控制方式。 然后还在smithpid基础上设计了LOS的曲线跟踪方法。 (有对应参考文献)。 有意者可直接联系,参考学习资料。 python语言。

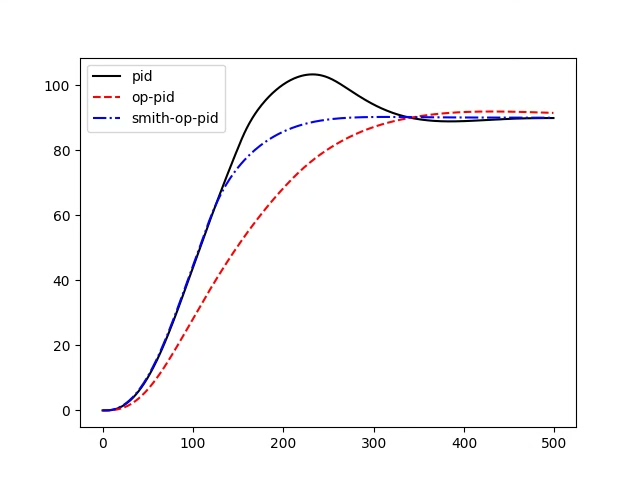
在无人船领域,精确的跟踪控制至关重要。今天咱们来聊聊基于无人船的Smith - PID跟踪控制,这其中涉及到对PID控制的改进,以及基于Smith - PID设计的LOS曲线跟踪方法。
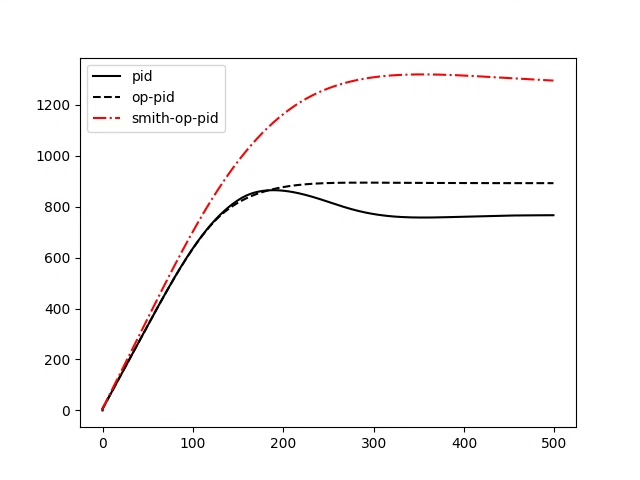
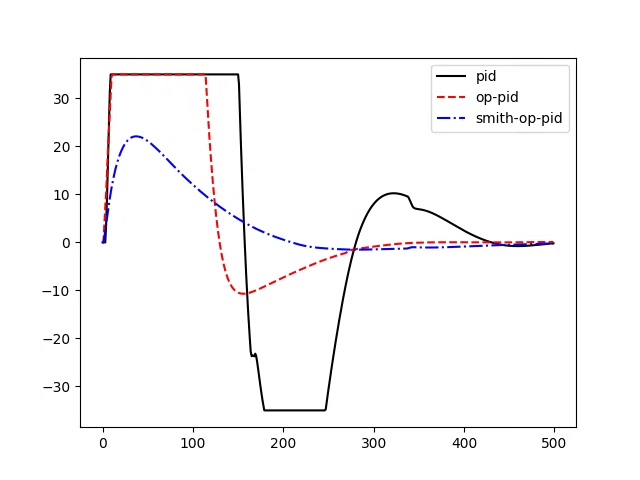
PID控制改进之三种方式
传统PID
PID控制算是控制领域的元老了,其核心公式为:
python
# 简单的传统PID控制代码示例
class PID:
def __init__(self, kp, ki, kd):
self.kp = kp
self.ki = ki
self.kd = kd
self.prev_error = 0
self.integral = 0
def update(self, setpoint, process_variable):
error = setpoint - process_variable
self.integral += error
derivative = error - self.prev_error
output = self.kp * error + self.ki * self.integral + self.kd * derivative
self.prev_error = error
return output这里,kp、ki、kd 分别是比例、积分、微分系数。比例项 kp error**能快速对误差做出反应;积分项 ki integral 用于消除稳态误差,随着时间积累误差的积分,让系统不断调整;微分项 kd * derivative 则根据误差的变化率提前做出调整,抑制超调。
最优PID
最优PID旨在寻找一组最佳的 kp、ki、kd 参数,以达到最优控制效果。这通常需要借助一些优化算法,比如遗传算法、粒子群算法等。假设有一个目标函数来评估控制效果(比如最小化误差的平方和),通过优化算法不断迭代调整 kp、ki、kd。以下是一个简单使用遗传算法优化PID参数的伪代码思路:
python
# 遗传算法优化PID参数伪代码
import numpy as np
# 目标函数,评估PID控制效果
def objective_function(kp, ki, kd):
# 假设这里有计算误差平方和的逻辑
pid = PID(kp, ki, kd)
total_error = 0
# 模拟系统运行,更新total_error
return total_error
# 遗传算法参数
population_size = 50
num_generations = 100
bounds = [(0, 10), (0, 10), (0, 10)] # kp, ki, kd的取值范围
# 初始化种群
population = np.random.uniform(bounds[0][0], bounds[0][1], (population_size, 3))
for generation in range(num_generations):
fitness = np.array([objective_function(kp, ki, kd) for kp, ki, kd in population])
selected_indices = np.argsort(fitness)[:int(population_size * 0.5)]
selected_population = population[selected_indices]
new_population = []
while len(new_population) < population_size:
parent1, parent2 = np.random.choice(selected_population, size = 2, replace = True)
child = (parent1 + parent2) / 2
new_population.append(child)
population = np.array(new_population)
best_kp, best_ki, best_kd = population[np.argmin([objective_function(kp, ki, kd) for kp, ki, kd in population])]通过遗传算法不断进化种群,最终找到能使目标函数最小的 kp、ki、kd,实现更优的控制。
基于Smith的PID
Smith预估器主要用于解决具有大纯滞后特性的系统控制问题。在无人船控制场景中,如果存在信号传输等滞后情况,Smith - PID就派上用场了。代码实现思路大致如下:
python
class SmithPID:
def __init__(self, kp, ki, kd, tau, theta):
self.kp = kp
self.ki = ki
self.kd = kd
self.tau = tau
self.theta = theta
self.prev_error = 0
self.integral = 0
self.prev_time = 0
def update(self, setpoint, process_variable, current_time):
error = setpoint - process_variable
self.integral += error * (current_time - self.prev_time)
derivative = (error - self.prev_error) / (current_time - self.prev_time)
# Smith预估部分
predicted_output = process_variable + (error - self.prev_error) * self.theta / self.tau
smith_error = setpoint - predicted_output
output = self.kp * smith_error + self.ki * self.integral + self.kd * derivative
self.prev_error = error
self.prev_time = current_time
return output这里的 tau 和 theta 分别是系统的时间常数和纯滞后时间。通过Smith预估部分,对未来的输出进行预估,提前补偿滞后的影响,从而提升控制性能。
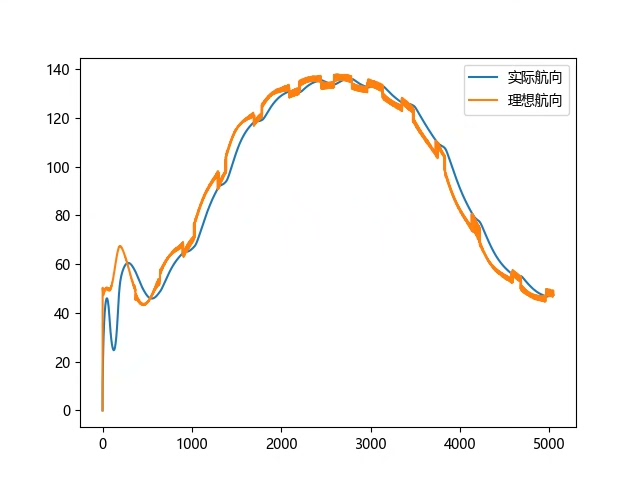
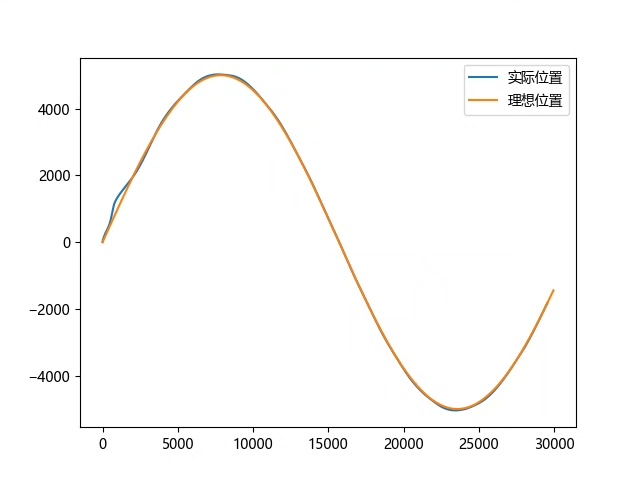
基于Smith - PID的LOS曲线跟踪方法
在Smith - PID基础上,设计LOS(Line - Of - Sight)曲线跟踪方法,能让无人船更好地沿着预设曲线行驶。基本原理是计算无人船当前位置与预设曲线上目标点的连线(视线),并调整无人船的航向以跟踪这条视线。以下是一个简单的LOS跟踪算法代码框架:
python
import math
# 假设无人船当前位置 (x, y),预设曲线上目标点 (target_x, target_y)
def los_control(x, y, target_x, target_y, speed):
distance = math.sqrt((target_x - x) ** 2 + (target_y - y) ** 2)
angle_to_target = math.atan2(target_y - y, target_x - x)
# 这里可以结合Smith - PID控制调整无人船航向
# 例如,将angle_to_target作为Smith - PID的输入设定值,当前航向作为反馈值
# 计算PID输出调整无人船的转向
# 这里简单假设直接根据距离调整速度
if distance < 10:
speed = 0.5 * speed
return angle_to_target, speed这个框架中,先计算无人船与目标点的距离和角度,然后根据情况调整速度,并利用Smith - PID控制无人船的转向,从而实现曲线跟踪。
感兴趣的小伙伴可以直接联系获取参考学习资料,咱们一起深入研究基于无人船的Smith - PID跟踪控制。希望这篇博文能为你在相关领域的探索提供一些思路。