在统计学和决策理论中,贝叶斯方法提供了一种强大的框架来量化证据的强度并更新我们的信念。本文将探讨如何使用贝叶斯因子和后验胜率来计算说服他人接受某个假设所需的数据量,并通过Python实例进行演示。
基本概念
先验胜率 (Prior Odds)
先验胜率表示在看到数据之前,两个假设相对可能性的比率:
先验胜率=P(H1)P(H0) \text{先验胜率} = \frac{P(H_1)}{P(H_0)} 先验胜率=P(H0)P(H1)
其中 H1H_1H1 是备择假设,H0H_0H0 是零假设。
贝叶斯因子 (Bayes Factor)
贝叶斯因子衡量数据对两个假设的支持程度:
BF10=P(Data∣H1)P(Data∣H0) BF_{10} = \frac{P(\text{Data} | H_1)}{P(\text{Data} | H_0)} BF10=P(Data∣H0)P(Data∣H1)
BF10>1BF_{10} > 1BF10>1 表示数据支持 H1H_1H1,值越大支持越强。
后验胜率 (Posterior Odds)
后验胜率是结合先验信念和数据证据后的胜率:
后验胜率=先验胜率×贝叶斯因子 \text{后验胜率} = \text{先验胜率} \times \text{贝叶斯因子} 后验胜率=先验胜率×贝叶斯因子
P(H1∣Data)P(H0∣Data)=P(H1)P(H0)×P(Data∣H1)P(Data∣H0) \frac{P(H_1|\text{Data})}{P(H_0|\text{Data})} = \frac{P(H_1)}{P(H_0)} \times \frac{P(\text{Data}|H_1)}{P(\text{Data}|H_0)} P(H0∣Data)P(H1∣Data)=P(H0)P(H1)×P(Data∣H0)P(Data∣H1)
实例分析:检验硬币是否公平
下面通过一个完整的Python实例演示如何计算说服他人相信硬币不公平所需的数据量。
问题设定
假设你想说服朋友相信一枚硬币是不公平的(正面朝上的概率不是50%)。你的朋友最初很怀疑,认为硬币有95%的可能性是公平的。
- H0H_0H0(零假设):硬币是公平的,P(正面)=0.5P(\text{正面}) = 0.5P(正面)=0.5
- H1H_1H1(备择假设):硬币是不公平的,P(正面)=0.7P(\text{正面}) = 0.7P(正面)=0.7
朋友的先验信念:
- P(H0)=0.95P(H_0) = 0.95P(H0)=0.95
- P(H1)=0.05P(H_1) = 0.05P(H1)=0.05
目标:使朋友相信 H1H_1H1 的后验概率达到90%
计算所需贝叶斯因子
python
import math
# 先验概率
prior_prob_h0 = 0.95
prior_prob_h1 = 0.05
# 先验胜率
prior_odds = prior_prob_h1 / prior_prob_h0
print(f"先验胜率: {prior_odds:.4f}")
# 目标后验概率和目标后验胜率
target_posterior_prob = 0.9
target_posterior_odds = target_posterior_prob / (1 - target_posterior_prob)
print(f"目标后验胜率: {target_posterior_odds:.2f}")
# 所需贝叶斯因子
required_bf = target_posterior_odds / prior_odds
print(f"所需贝叶斯因子: {required_bf:.2f}")计算贝叶斯因子函数
python
from scipy.stats import binom
def calculate_bf(n, k, p_h1=0.7):
"""
计算贝叶斯因子
n: 抛硬币次数
k: 正面朝上次数
p_h1: H₁假设下正面概率
"""
# H₀下的似然 (公平硬币)
likelihood_h0 = binom.pmf(k, n, 0.5)
# H₁下的似然 (不公平硬币)
likelihood_h1 = binom.pmf(k, n, p_h1)
# 避免除以零
if likelihood_h0 == 0:
return float('inf')
return likelihood_h1 / likelihood_h0
# 测试计算贝叶斯因子
n_test, k_test = 10, 7
bf_test = calculate_bf(n_test, k_test)
print(f"{n_test}次抛硬币中{k_test}次正面的贝叶斯因子: {bf_test:.3f}")寻找最小样本量
python
from scipy.stats import binom
def calculate_bf(n, k, p_h1=0.7):
"""
计算贝叶斯因子
n: 抛硬币次数
k: 正面朝上次数
p_h1: H₁假设下正面概率
"""
# H₀下的似然 (公平硬币)
likelihood_h0 = binom.pmf(k, n, 0.5)
# H₁下的似然 (不公平硬币)
likelihood_h1 = binom.pmf(k, n, p_h1)
# 避免除以零
if likelihood_h0 == 0:
return float('inf')
return likelihood_h1 / likelihood_h0
# 测试计算贝叶斯因子
n_test, k_test = 10, 7
bf_test = calculate_bf(n_test, k_test)
print(f"{n_test}次抛硬币中{k_test}次正面的贝叶斯因子: {bf_test:.3f}")
def find_min_sample_size(prior_prob_h1, target_posterior_prob, p_h1=0.7, max_n=100):
"""
找到达到目标后验概率所需的最小样本量
"""
# 计算所需贝叶斯因子
prior_odds = prior_prob_h1 / (1 - prior_prob_h1)
target_posterior_odds = target_posterior_prob / (1 - target_posterior_prob)
required_bf = target_posterior_odds / prior_odds
print(f"先验概率 P(H₁): {prior_prob_h1}")
print(f"目标后验概率 P(H₁|Data): {target_posterior_prob}")
print(f"所需贝叶斯因子: {required_bf:.2f}")
# 尝试不同的样本量
for n in range(1, max_n + 1):
# 考虑最有利于H₁的情况 (全部正面)
k = n
bf = calculate_bf(n, k, p_h1)
if bf >= required_bf:
return n, k, bf
return None, None, None
# 计算最小样本量
min_n, min_k, achieved_bf = find_min_sample_size(0.05, 0.9)
print(f"\n需要至少{min_n}次实验,且全部正面朝上")
print(f"此时贝叶斯因子: {achieved_bf:.2f}")验证后验概率
python
from scipy.stats import binom
def calculate_bf(n, k, p_h1=0.7):
"""
计算贝叶斯因子
n: 抛硬币次数
k: 正面朝上次数
p_h1: H₁假设下正面概率
"""
# H₀下的似然 (公平硬币)
likelihood_h0 = binom.pmf(k, n, 0.5)
# H₁下的似然 (不公平硬币)
likelihood_h1 = binom.pmf(k, n, p_h1)
# 避免除以零
if likelihood_h0 == 0:
return float('inf')
return likelihood_h1 / likelihood_h0
def find_min_sample_size(prior_prob_h1, target_posterior_prob, p_h1=0.7, max_n=100):
"""
找到达到目标后验概率所需的最小样本量
"""
# 计算所需贝叶斯因子
prior_odds = prior_prob_h1 / (1 - prior_prob_h1)
target_posterior_odds = target_posterior_prob / (1 - target_posterior_prob)
required_bf = target_posterior_odds / prior_odds
print(f"先验概率 P(H₁): {prior_prob_h1}")
print(f"目标后验概率 P(H₁|Data): {target_posterior_prob}")
print(f"所需贝叶斯因子: {required_bf:.2f}")
# 尝试不同的样本量
for n in range(1, max_n + 1):
# 考虑最有利于H₁的情况 (全部正面)
k = n
bf = calculate_bf(n, k, p_h1)
if bf >= required_bf:
return n, k, bf
return None, None, None
# 计算最小样本量
min_n, min_k, achieved_bf = find_min_sample_size(0.05, 0.9)
def update_belief(prior_prob_h1, n, k, p_h1=0.7):
"""
更新后验概率
"""
# 计算贝叶斯因子
bf = calculate_bf(n, k, p_h1)
# 先验胜率
prior_odds = prior_prob_h1 / (1 - prior_prob_h1)
# 后验胜率
posterior_odds = prior_odds * bf
# 后验概率
posterior_prob_h1 = posterior_odds / (1 + posterior_odds)
return posterior_prob_h1
# 验证后验概率
prior_prob_h1 = 0.05
n = min_n
k = min_k
posterior_prob = update_belief(prior_prob_h1, n, k)
print(f"先验概率 P(H₁): {prior_prob_h1:.4f}")
print(f"经过{n}次实验(全部正面)后")
print(f"后验概率 P(H₁|Data): {posterior_prob:.4f}")可视化不同实验结果的影响
python
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 测试不同的正面次数
n = min_n
results = range(0, n+1)
posterior_probs = [update_belief(prior_prob_h1, n, k) for k in results]
plt.figure(figsize=(10, 6))
plt.plot(results, posterior_probs, 'o-', linewidth=2, markersize=6)
plt.axhline(y=target_posterior_prob, color='r', linestyle='--', label='目标概率 (90%)')
plt.xlabel('正面朝上的次数')
plt.ylabel('后验概率 P(H₁|Data)')
plt.title(f'抛硬币{n}次后的后验概率变化')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()比较不同先验信念的影响
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
def calculate_bf(n, k, p_h1=0.7):
"""
计算贝叶斯因子
n: 抛硬币次数
k: 正面朝上次数
p_h1: H₁假设下正面概率
"""
# H₀下的似然 (公平硬币)
likelihood_h0 = binom.pmf(k, n, 0.5)
# H₁下的似然 (不公平硬币)
likelihood_h1 = binom.pmf(k, n, p_h1)
# 避免除以零
if likelihood_h0 == 0:
return float('inf')
return likelihood_h1 / likelihood_h0
def find_min_sample_size(prior_prob_h1, target_posterior_prob, p_h1=0.7, max_n=100):
"""
找到达到目标后验概率所需的最小样本量
"""
# 计算所需贝叶斯因子
prior_odds = prior_prob_h1 / (1 - prior_prob_h1)
target_posterior_odds = target_posterior_prob / (1 - target_posterior_prob)
required_bf = target_posterior_odds / prior_odds
print(f"先验概率 P(H₁): {prior_prob_h1}")
print(f"目标后验概率 P(H₁|Data): {target_posterior_prob}")
print(f"所需贝叶斯因子: {required_bf:.2f}")
# 尝试不同的样本量
for n in range(1, max_n + 1):
# 考虑最有利于H₁的情况 (全部正面)
k = n
bf = calculate_bf(n, k, p_h1)
if bf >= required_bf:
return n, k, bf
return None, None, None
# 比较不同先验信念下所需样本量
prior_beliefs = [0.01, 0.05, 0.1, 0.3, 0.5]
target_prob = 0.9
p_h1 = 0.7
results = []
for prior in prior_beliefs:
n_needed, k_needed, bf_achieved = find_min_sample_size(prior, target_prob, p_h1)
if n_needed:
results.append((prior, n_needed, bf_achieved))
print(f"先验概率 {prior:.2f} -> 需要{n_needed}次实验")
# 可视化结果
priors = [r[0] for r in results]
n_trials = [r[1] for r in results]
plt.figure(figsize=(10, 6))
plt.plot(priors, n_trials, 'o-', linewidth=2, markersize=8)
plt.xlabel('先验概率 P(H₁)')
plt.ylabel('所需实验次数')
plt.title('不同先验信念下所需样本量')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()贝叶斯因子与p值的比较
为了更好地理解贝叶斯因子的意义,我们可以将其与传统的p值方法进行比较。
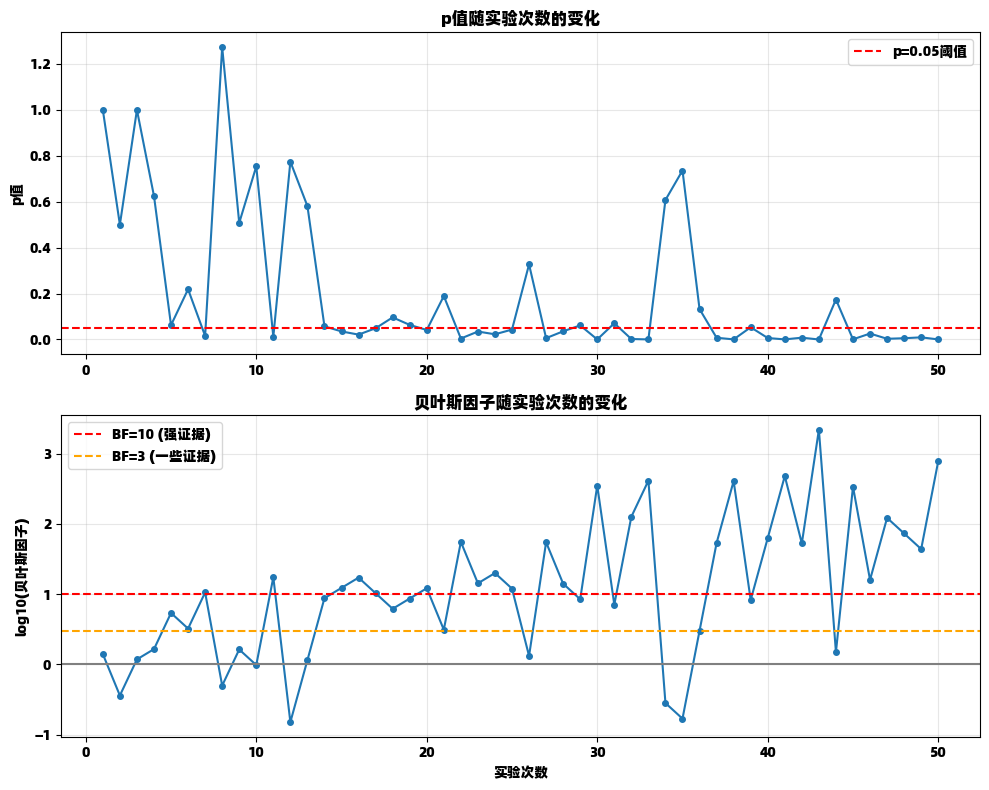
python
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.stats import binom
def calculate_bf(n, k, p_h1=0.7):
"""
计算贝叶斯因子
n: 抛硬币次数
k: 正面朝上次数
p_h1: H₁假设下正面概率
"""
# H₀下的似然 (公平硬币)
likelihood_h0 = binom.pmf(k, n, 0.5)
# H₁下的似然 (不公平硬币)
likelihood_h1 = binom.pmf(k, n, p_h1)
# 避免除以零
if likelihood_h0 == 0:
return float('inf')
return likelihood_h1 / likelihood_h0
def simulate_experiments(n_trials, p_true=0.7):
"""
模拟多次实验并计算p值和贝叶斯因子
"""
p_values = []
bayes_factors = []
for n in range(1, n_trials + 1):
# 模拟实验 (二项分布)
k = np.random.binomial(n, p_true)
# 计算p值 (双侧检验)
p_val = 2 * min(binom.cdf(k, n, 0.5), 1 - binom.cdf(k-1, n, 0.5))
p_values.append(p_val)
# 计算贝叶斯因子
bf = calculate_bf(n, k, p_true)
bayes_factors.append(bf)
return p_values, bayes_factors
# 模拟实验
np.random.seed(42)
n_trials = 50
p_values, bayes_factors = simulate_experiments(n_trials)
# 绘制结果
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# p值图
ax1.plot(range(1, n_trials+1), p_values, 'o-', markersize=4)
ax1.axhline(y=0.05, color='r', linestyle='--', label='p=0.05阈值')
ax1.set_ylabel('p值')
ax1.set_title('p值随实验次数的变化')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 贝叶斯因子图
ax2.plot(range(1, n_trials+1), np.log10(bayes_factors), 'o-', markersize=4)
ax2.axhline(y=0, color='gray', linestyle='-')
ax2.axhline(y=math.log10(10), color='r', linestyle='--', label='BF=10 (强证据)')
ax2.axhline(y=math.log10(3), color='orange', linestyle='--', label='BF=3 (一些证据)')
ax2.set_xlabel('实验次数')
ax2.set_ylabel('log10(贝叶斯因子)')
ax2.set_title('贝叶斯因子随实验次数的变化')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()结论
贝叶斯因子和后验胜率提供了了一种强大的方法来量化证据的强度并确定支持某个假设所需的数据量。与传统的频率学派方法相比,贝叶斯方法具有几个重要优势:
-
直接回答相关问题:贝叶斯方法直接计算假设为真的概率,而不是基于零假设的p值。
-
纳入先验知识:通过先验分布,贝叶斯方法可以纳入现有的知识或信念。
-
顺序更新:贝叶斯更新可以随着新数据的到来而连续进行,非常适合迭代实验设计。
-
样本量确定:通过计算达到特定后验概率或贝叶斯因子所需的数据量,可以更有效地设计实验。
本文通过硬币实验的实例展示了如何使用Python计算贝叶斯因子、后验概率以及确定所需样本量。这些方法可以广泛应用于假设检验、A/B测试、科学实验设计等领域,帮助研究人员和决策者更有效地规划实验和解释结果。
需要注意的是,贝叶斯分析的结果依赖于先验分布的选择,因此在使用时应谨慎考虑先验的合理性,并进行敏感性分析以确保结论的稳健性。