文章目录
-
- [📋 题目](#📋 题目)
- [🔑 一、理解关键概念](#🔑 一、理解关键概念)
-
- [1.1 d(v) 是什么?](#1.1 d(v) 是什么?)
- [1.2 π(v) 是什么?](#1.2 π(v) 是什么?)
- [📊 二、新的例题](#📊 二、新的例题)
- [🎯 三、关键问题解答](#🎯 三、关键问题解答)
- [📝 四、总结](#📝 四、总结)
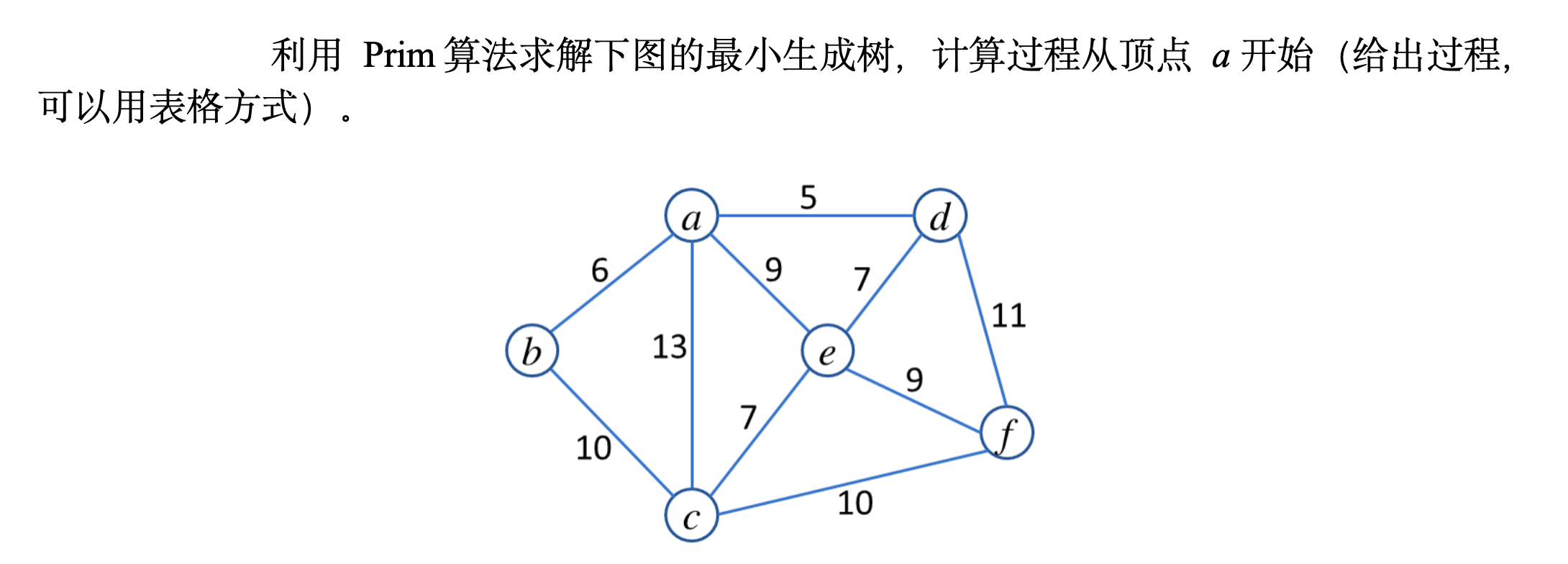
📋 题目
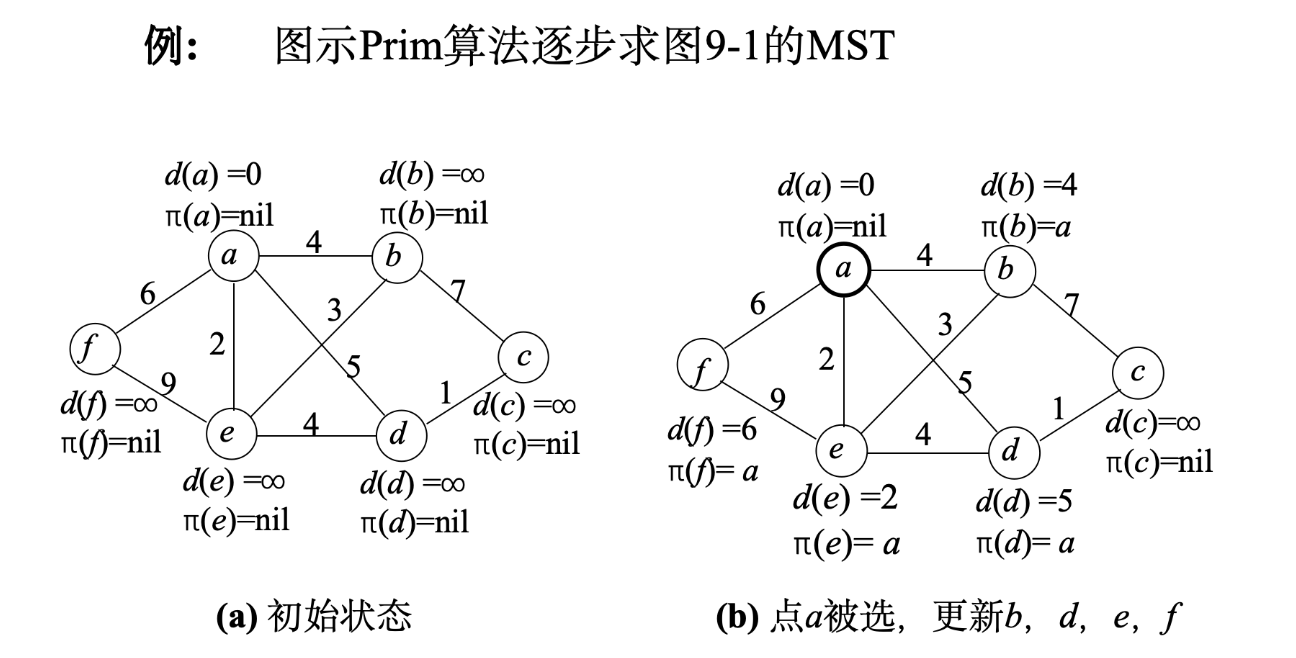
🔑 一、理解关键概念
1.1 d(v) 是什么?
d(v) 的含义:
- 当前已知的 ,从顶点v到已连通区域 的最短距离
- 如果v已经在连通区域中,d(v) = 0
- 如果v还没连通,d(v) = 从v到连通区域的某条边的最小权重
通俗理解:
- 就像"从村庄v到已修路区域,最便宜的路要花多少钱"
- 初始时,除了起始点,其他点的d值都是∞(无穷大)
1.2 π(v) 是什么?
π(v) 的含义:
- 父节点 :在已连通区域中,哪个顶点 通过权重为d(v)的边连接到v
- 如果v已经在连通区域中,π(v) = nil(没有父节点,或者是起始点)
通俗理解:
- 就像"从哪个村庄修路到v最便宜"
- 如果d(v) = 4, π(v) = a,意思是"从a修路到v,成本是4"
关键关系:
- 边 (π(v), v) 的权重 = d(v)
- 这条边就是"当前已知的,连接v到连通区域的最便宜的路"
📊 二、新的例题
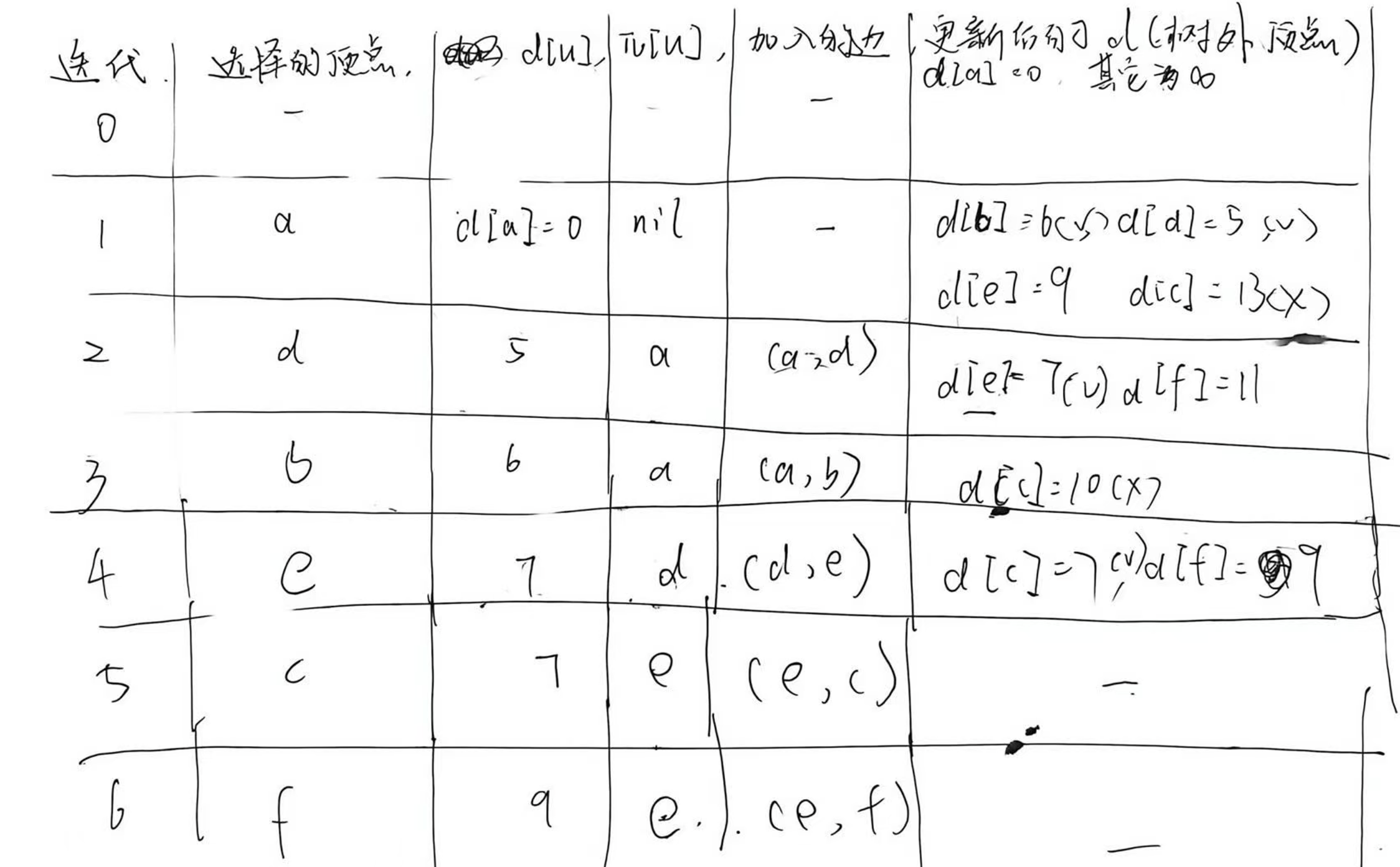
🎯 三、关键问题解答
Q1:d(V)更新的逻辑是什么?
更新规则:
对于新加入连通区域的顶点u,检查它的每个邻居v:
如果 v 还没连通(v不在连通区域中):
如果 w(u,v) < d(v):
更新:d(v) = w(u,v)
更新:π(v) = u通俗理解:
- "如果从u到v的路,比v当前已知的最便宜的路更便宜"
- "就更新v的距离和父节点"
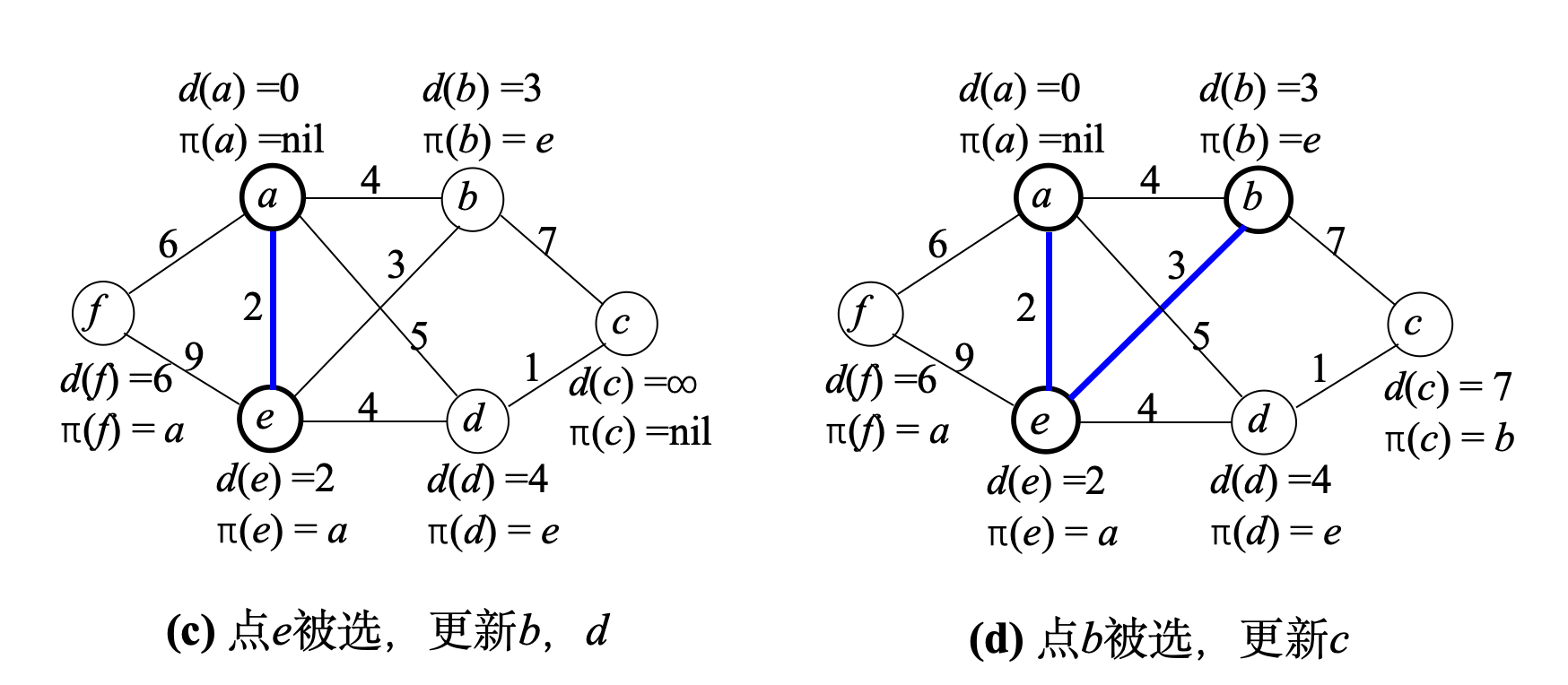
例子:步骤©中更新d
- 选择e后,检查e → d
- d当前:d(d) = 5(从a到d)
- e → d:权重4
- 因为4 < 5,所以更新:d(d) = 4,π(d) = e
Q2:为什么选择某个点?
选择规则 :从所有未连通的顶点中,选择d值最小的
为什么这样选择?
贪心思想:
- d值最小 = 连接到连通区域最便宜
- 每次选择最便宜的,保证总成本最小
证明思路(简化):
- 假设存在更优的方案,不选择d值最小的点
- 那么必然存在一条更便宜的路
- 但我们选择的是d值最小的,矛盾!
- 所以选择d值最小的是最优的
例子:步骤(c)中选择e
- 未连通顶点:{b, c, d, e, f}
- d值:b=4, c=∞, d=5, e=2, f=6
- e的d值最小(2),所以选择e
Q4:π值什么时候改变?
π值改变的条件:
- 初始时:所有顶点的π = nil
- 第一次发现路径 :当某个顶点v第一次被发现可以连接到连通区域时
- 例如:步骤(b)中,b第一次被发现,π(b) = a
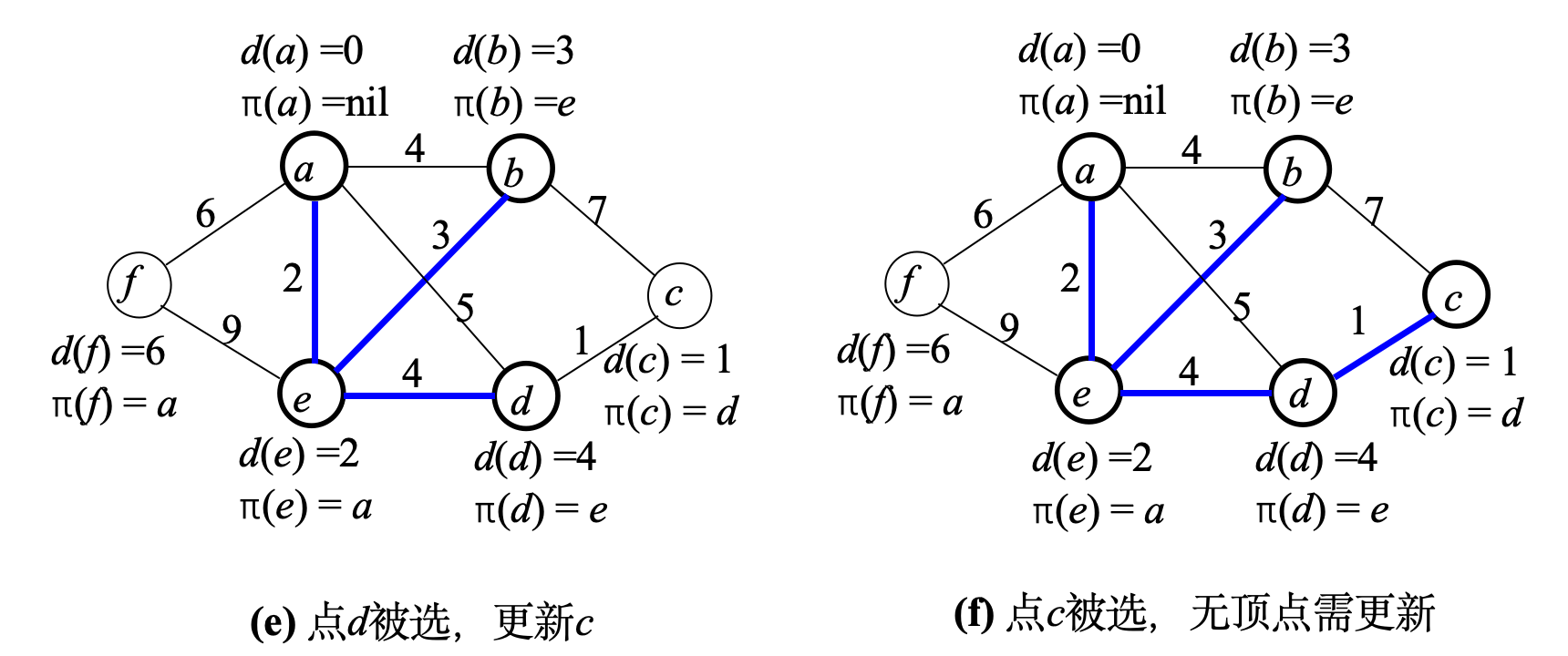
- 发现更便宜的路径 :当发现从新顶点u到v的路,比v当前已知的路更便宜时
- 例如:步骤©中,发现e → d(4)比a → d(5)便宜,所以π(d)从a改为e
π值不变的情况:
- 如果新发现的路径不比当前已知的路径便宜,π值不变
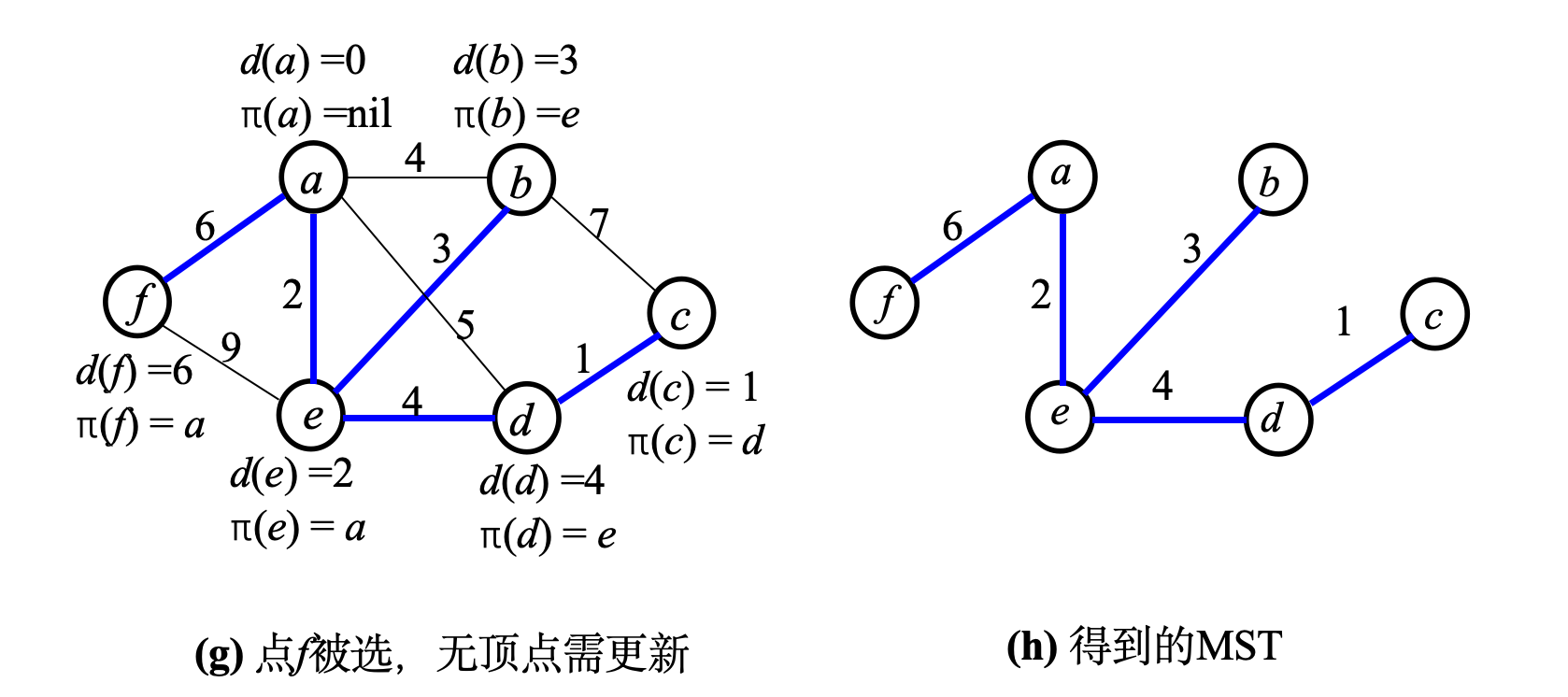
- 例如:步骤©中,e → f(9)不比a → f(6)便宜,所以π(f)保持为a
📝 四、总结
核心概念
- d(v):从v到连通区域的最短距离(当前已知的)
- π(v):v的父节点,通过权重为d(v)的边连接到v
- 选择规则:每次选择d值最小的未连通顶点
- 更新规则:如果发现更便宜的路径,更新d和π值
算法流程
1. 初始化:选择起始点a,d(a)=0,其他d(v)=∞
2. 重复直到所有顶点连通:
a. 选择d值最小的未连通顶点u
b. 把u加入连通区域,修路(π(u), u)
c. 更新u的邻居:如果发现更便宜的路径,更新d和π
3. 返回MST关键理解
- 贪心策略:每次选择最便宜的,得到全局最优
- 动态更新:随着连通区域扩大,不断发现更便宜的路径
- π值记录最优路径:π(v)记录"当前已知的,连接v到连通区域的最便宜的方式"
💡 记忆要点:d值记录距离,π值记录父节点,选择最小d值,更新更便宜路径!