从0开始学算法——第十六天（双指针算法）

写在开头的话

学习了昨天的滑动窗口之后，今天让我们来一起学习一下双指针算法吧。

知识点：

（1）合并两个有序数组（2）合并区间（3）输入有序数组

合并两个有序数组

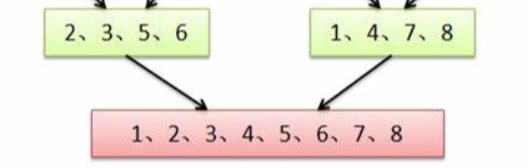
在算法竞赛中，合并两个有序数组是一个常见的问题，使用双指针方法可以高效地解决。这种方法利用了两个有序数组的有序性质，通过同时遍历两个数组，逐步将它们合并为一个有序数组。

具体步骤

初始化指针：

设定两个指针分别指向两个有序数组的起始位置。通常将它们分别命名为 p1 和 p2。

比较指针所指元素：

比较 nums1[p1] 和 nums2[p2] 的大小。
如果 nums1[p1] <= nums2[p2]，则将 nums1[p1] 加入合并后的数组，并将 p1 指针向后移动一位。
如果 nums1[p1] > nums2[p2]，则将 nums2[p2] 加入合并后的数组，并将 p2 指针向后移动一位。

遍历直到其中一个数组遍历结束：

继续进行比较和移动指针的操作，直到 p1 指针或 p2 指针超出了数组的范围。

处理剩余元素：

如果有一个数组的元素已经全部合并完毕，而另一个数组还有剩余元素，直接将剩余元素依次加入合并后的数组即可。

返回合并后的数组：

返回合并后的有序数组。

代码实现

C++代码实现

cpp 复制代码

#include <iostream>
#include <vector>

using namespace std;

vector<int> merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int p1 = m - 1;
    int p2 = n - 1;
    int p = m + n - 1;

    while (p1 >= 0 && p2 >= 0) {
        if (nums1[p1] > nums2[p2]) {
            nums1[p] = nums1[p1];
            p1--;
        } else {
            nums1[p] = nums2[p2];
            p2--;
        }
        p--;
    }

    for (int i = 0; i <= p2; i++) {
        nums1[i] = nums2[i];
    }

    return nums1;
}

int main() {
    vector<int> nums1 = {1, 3, 5, 0, 0, 0};
    int m = 3;
    vector<int> nums2 = {2, 4, 6};
    int n = 3;
    merge(nums1, m, nums2, n);

    for (int num : nums1) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

Java代码实现

java 复制代码

#include <iostream>
#include <vector>

using namespace std;

vector<int> merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int p1 = m - 1;
    int p2 = n - 1;
    int p = m + n - 1;

    while (p1 >= 0 && p2 >= 0) {
        if (nums1[p1] > nums2[p2]) {
            nums1[p] = nums1[p1];
            p1--;
        } else {
            nums1[p] = nums2[p2];
            p2--;
        }
        p--;
    }

    for (int i = 0; i <= p2; i++) {
        nums1[i] = nums2[i];
    }

    return nums1;
}

int main() {
    vector<int> nums1 = {1, 3, 5, 0, 0, 0};
    int m = 3;
    vector<int> nums2 = {2, 4, 6};
    int n = 3;
    merge(nums1, m, nums2, n);

    for (int num : nums1) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

Python代码实现

python 复制代码

def merge(nums1, m, nums2, n):
    p1 = m - 1
    p2 = n - 1
    p = m + n - 1

    while p1 >= 0 and p2 >= 0:
        if nums1[p1] > nums2[p2]:
            nums1[p] = nums1[p1]
            p1 -= 1
        else:
            nums1[p] = nums2[p2]
            p2 -= 1
        p -= 1

    nums1[:p2 + 1] = nums2[:p2 + 1]

    return nums1

nums1 = [1, 3, 5, 0, 0, 0]
m = 3
nums2 = [2, 4, 6]
n = 3
merge(nums1, m, nums2, n)
print(nums1)

运行结果

合并区间

题目描述

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

解法

首先，我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入 merged 数组中，并按顺序依次考虑之后的每个区间：

如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；

否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。

代码实现

C++代码实现

cpp 复制代码

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) {
            return {};
        }
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> merged;
        for (int i = 0; i < intervals.size(); ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (!merged.size() || merged.back()[1] < L) {
                merged.push_back({L, R});
            }
            else {
                merged.back()[1] = max(merged.back()[1], R);
            }
        }
        return merged;
    }
};

Java代码实现

java 复制代码

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0) {
            return new int[0][2];
        }
        Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });
        List<int[]> merged = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
                merged.add(new int[]{L, R});
            } else {
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

Python代码实现

python 复制代码

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x: x[0])

        merged = []
        for interval in intervals:
            # 如果列表为空，或者当前区间与上一区间不重合，直接添加
            if not merged or merged[-1][1] < interval[0]:
                merged.append(interval)
            else:
                # 否则的话，我们就可以与上一区间进行合并
                merged[-1][1] = max(merged[-1][1], interval[1])

        return merged

输入有序数组

题目描述

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

解法

初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和，并和目标值比较。如果两个元素之和等于目标值，则发现了唯一解。如果两个元素之和小于目标值，则将左侧指针右移一位。如果两个元素之和大于目标值，则将右侧指针左移一位。移动指针之后，重复上述操作，直到找到答案。

使用双指针的实质是缩小查找范围。那么会不会把可能的解过滤掉？答案是不会。假设 numbers[i]+numbers[j]=target 是唯一解，其中 0≤i<j≤numbers.length−1。初始时两个指针分别指向下标 0 和下标 numbers.length−1，左指针指向的下标小于或等于 i，右指针指向的下标大于或等于 j。除非初始时左指针和右指针已经位于下标 i 和 j，否则一定是左指针先到达下标 i 的位置或者右指针先到达下标 j 的位置。

如果左指针先到达下标 i 的位置，此时右指针还在下标 j 的右侧，sum>targetsum>targetsum>target，因此一定是右指针左移，左指针不可能移到 i 的右侧。

如果右指针先到达下标 j 的位置，此时左指针还在下标 i 的左侧，sum<targetsum<targetsum<target，因此一定是左指针右移，右指针不可能移到 j 的左侧。

由此可见，在整个移动过程中，左指针不可能移到 i 的右侧，右指针不可能移到 j的左侧，因此不会把可能的解过滤掉。由于题目确保有唯一的答案，因此使用双指针一定可以找到答案。

代码实现

C++代码实现

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int low = 0, high = numbers.size() - 1;
        while (low < high) {
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return {low + 1, high + 1};
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return {-1, -1};
    }
};

Java代码实现

java 复制代码

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int low = 0, high = numbers.length - 1;
        while (low < high) {
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return new int[]{low + 1, high + 1};
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return new int[]{-1, -1};
    }
}

Python代码实现

python 复制代码

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        low, high = 0, len(numbers) - 1
        while low < high:
            total = numbers[low] + numbers[high]
            if total == target:
                return [low + 1, high + 1]
            elif total < target:
                low += 1
            else:
                high -= 1

        return [-1, -1]

简单总结

本文主要解决了双指针算法的几个经典题目。在对于朴素做法来说是 O()的做法来说，如果对于另外一层循环是存在单调性的情况下，可以考虑使用双指针算法。