探索数字编码超表面：多模式复用与多功能实现

数字编码超表面多模式复用轨道角动量多焦点透镜多功能复用相位计算分布远场计算代码相位分布计算代码多通道轨道角动量相位分布代码不需要cst仿真，可以直接根据相位matlab计算远场

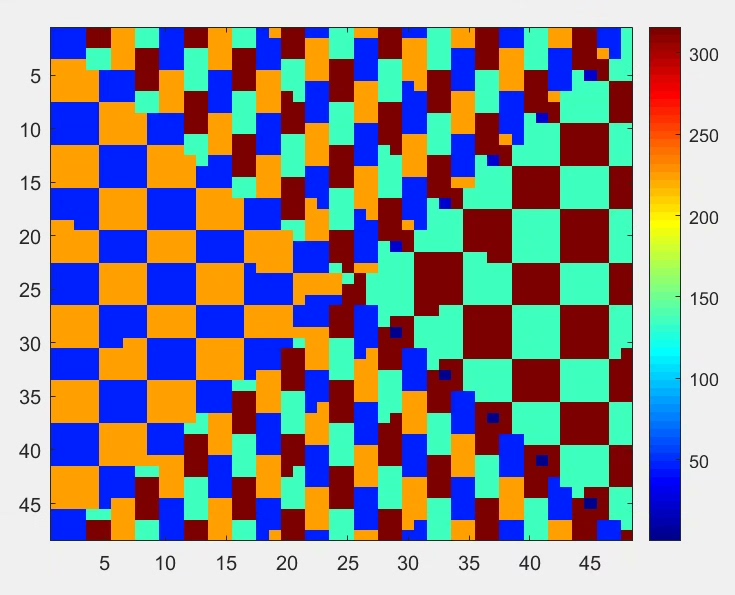
在现代光学领域，数字编码超表面正逐渐展现出其独特的魅力与无限潜力。今天咱们就来聊聊数字编码超表面在多模式复用轨道角动量、多焦点透镜以及多功能复用相位计算分布等方面的奇妙之处，还会分享相关的代码，让大家能更直观地感受其原理。

多模式复用轨道角动量

轨道角动量（OAM）在光通信、光学成像等诸多领域有着重要的应用前景。通过数字编码超表面实现多模式复用轨道角动量，能够极大地提升信息传输的容量和效率。在这个过程中，我们需要精确地控制光的相位分布，以实现不同模式的轨道角动量复用。

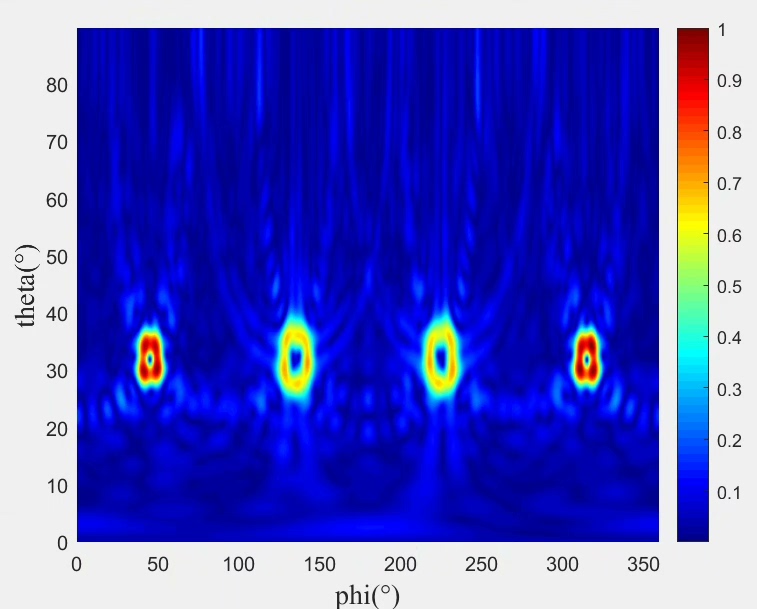
比如说，在计算多通道轨道角动量相位分布时，我们可以用如下Matlab代码来实现：

matlab 复制代码

% 参数设置
lambda = 532e - 9; % 波长
k = 2 * pi / lambda;
radius = 1e - 3; % 超表面半径
N = 1000; % 采样点数
theta = linspace(0, 2 * pi, N);
r = linspace(0, radius, N);
[R, Theta] = meshgrid(r, theta);

% 不同模式的轨道角动量相位分布计算
l = 1; % 轨道角动量模式数
phase = l * Theta;

% 绘制相位分布
figure;
surf(R, Theta, phase);
shading interp;
xlabel('r (m)');
ylabel('theta (rad)');
zlabel('Phase (rad)');
title(['OAM mode l = ', num2str(l)]);

代码分析：首先我们定义了一些基本参数，如波长 lambda、波数 k、超表面半径 radius 以及采样点数 N。然后通过 linspace 函数生成极坐标下的采样点 theta 和 r，再利用 meshgrid 函数生成网格数据。接着，根据轨道角动量模式数 l 来计算相位分布 phase，这里简单地使用了 l * Theta 的关系，不同的 l 值就对应不同的轨道角动量模式。最后，使用 surf 函数绘制出相位分布的三维图形，方便我们直观观察。

多焦点透镜

数字编码超表面还能实现多焦点透镜的功能。传统透镜只能形成单一焦点，而多焦点透镜在光镊、三维成像等领域有着独特的优势。实现多焦点透镜的关键同样在于对相位分布的精确控制。

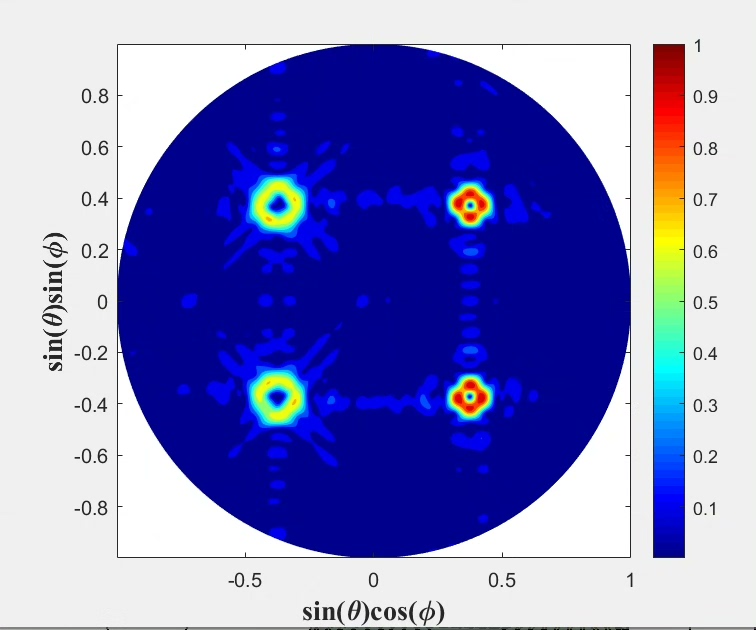
下面看看相位分布计算代码，这里以双焦点透镜为例：

matlab 复制代码

% 参数设置
lambda = 532e - 9;
k = 2 * pi / lambda;
radius = 1e - 3;
N = 1000;
theta = linspace(0, 2 * pi, N);
r = linspace(0, radius, N);
[R, Theta] = meshgrid(r, theta);

% 第一个焦点位置
z1 = 0.1; % 焦点1在z轴上的位置
k1 = k * (1 - R.^2 / (2 * z1));
phase1 = k1 * R.^2;

% 第二个焦点位置
z2 = 0.2; % 焦点2在z轴上的位置
k2 = k * (1 - R.^2 / (2 * z2));
phase2 = k2 * R.^2;

% 总的相位分布
total_phase = phase1 + phase2;

% 绘制相位分布
figure;
surf(R, Theta, total_phase);
shading interp;
xlabel('r (m)');
ylabel('theta (rad)');
zlabel('Phase (rad)');
title('Dual - focus lens phase distribution');

代码分析：依旧是先设定基本参数。然后分别针对两个焦点计算相位分布，根据球面波的相位关系，通过不同的 z 值（焦点在 z 轴上的位置）来计算 k1 和 k2，进而得到 phase1 和 phase2。最后将两个焦点的相位相加得到总的相位分布 total_phase，并绘制出三维相位分布图形，展示双焦点透镜所需的相位分布情况。

多功能复用相位计算分布

多功能复用相位计算分布整合了上述多种功能，通过巧妙的算法和相位调控，让数字编码超表面在同一器件上实现多种功能。这对于提升光学器件的集成度和实用性具有重要意义。

远场计算代码

我们可以直接根据相位利用Matlab计算远场，以下是一个简单的远场计算代码示例：

matlab 复制代码

% 参数设置
lambda = 532e - 9;
k = 2 * pi / lambda;
z = 1; % 观察平面距离超表面的距离
radius = 1e - 3;
N = 1000;
theta = linspace(0, 2 * pi, N);
r = linspace(0, radius, N);
[R, Theta] = meshgrid(r, theta);

% 假设已经有相位分布，这里简单生成一个示例相位
phase = R.^2; 

% 远场计算
x_far = linspace(-0.01, 0.01, N);
y_far = linspace(-0.01, 0.01, N);
[X_far, Y_far] = meshgrid(x_far, y_far);
E_far = zeros(size(X_far));

for m = 1:size(R, 1)
    for n = 1:size(R, 2)
        r_prime = [R(m, n) * cos(Theta(m, n)); R(m, n) * sin(Theta(m, n)); 0];
        r = [X_far; Y_far; z];
        k_dot_r_prime = k * dot(r_prime, r) / norm(r);
        E_far = E_far + exp(1i * (k * norm(r) - k_dot_r_prime + phase(m, n))) / norm(r);
    end
end

% 绘制远场强度分布
figure;
intensity = abs(E_far).^2;
surf(X_far, Y_far, intensity);
shading interp;
xlabel('x (m)');
ylabel('y (m)');
zlabel('Intensity (a.u.)');
title('Far - field intensity distribution');

代码分析：先设定好波长、观察距离等参数。假设有一个相位分布 phase（这里简单用 R.^2 来示意）。通过两个嵌套循环遍历超表面上的每一个点，计算该点到远场观察平面上各点的光传播相位，再叠加所有点的贡献得到远场电场分布 E_far。最后通过计算电场强度的模平方得到远场强度分布 intensity，并绘制出三维远场强度分布图形。

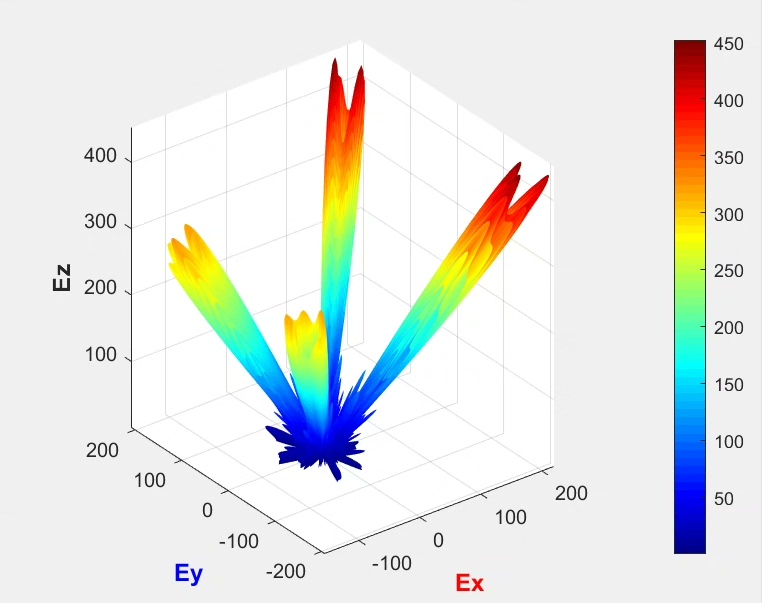
综上所述，数字编码超表面在多模式复用轨道角动量、多焦点透镜以及多功能复用相位计算分布等方面展现出巨大的应用价值，通过Matlab代码我们能更深入理解其原理与实现过程，期待未来能看到更多基于此的创新应用。