在强化学习(Reinforcement Learning, RL)的浩瀚兵器谱中,REINFORCE(又名蒙特卡洛策略梯度)往往被安排在角落里。
大多数 RL 课程的讲师在介绍它时,都会遵循一个固定的脚本:先把它作为策略梯度(Policy Gradient)的鼻祖请出来,展示一下公式,然后迅速开始"批判大会"------批判它方差大、收敛慢、样本效率极低。最后,讲师会大手一挥:"所以,我们在实战中通常使用 Actor-Critic 或 PPO。"
这种叙事方式给初学者留下了一个根深蒂固的印象:REINFORCE 只是一个因为早期技术不成熟而诞生的"粗糙版本",是一个被时代淘汰的古董。
但如果你深入研读过 Silver、Sutton 甚至 OpenAI 的核心论文,你会发现 REINFORCE 的幽灵从未消失。事实上,它是理解现代 RL 算法的第一性原理(First Principle)。在如今的大模型 RLHF(基于人类反馈的强化学习)微调中,REINFORCE 的变体依然扮演着幕后英雄的角色。
今天,我们要剥开那些复杂的现代技巧,重回 1992 年 Ronald Williams 提出它的那一刻,看看这个所谓的"粗糙算法",究竟隐藏着怎样惊人的数学美感与顽强的生命力。
第一章:数学的优雅------"对数导数技巧"的魔法
很多人觉得 REINFORCE "粗糙",是因为它的核心逻辑听起来太像"碰运气":试一试,好就奖励,坏就惩罚。但这种直觉背后,支撑它的是一个极其漂亮且严格的数学推导。
我们要解决的核心问题是:如何对一个采样出来的、离散的动作序列求导?
在监督学习中,目标函数 y=f(x)y=f(x)y=f(x) 通常是平滑的,链式法则(Backpropagation)随便用。但在 RL 中,环境反馈的回报 J(θ)J(\theta)J(θ) 是基于一个概率分布采样的结果:
J(θ)=Eτ∼πθ[R(τ)] J(\theta) = \mathbb{E}{\tau \sim \pi\theta}[R(\tau)] J(θ)=Eτ∼πθ[R(τ)]
这里的 τ\tauτ 是轨迹,πθ\pi_\thetaπθ 是你的策略网络。因为"采样"这个操作是不可导的,我们似乎碰到了死胡同。
REINFORCE 使用了著名的 Log-Derivative Trick(对数导数技巧),将不可能变成了可能:
∇θE[R]=E[R(τ)∇θlogπθ(τ)] \nabla_\theta \mathbb{E}[R] = \mathbb{E} [ R(\tau) \nabla_\theta \log \pi_\theta(\tau) ] ∇θE[R]=E[R(τ)∇θlogπθ(τ)]
这个公式的优雅之处在于,它把梯度的计算,转化为了**"期望下的加权"**。它不需要知道环境是怎么运作的(Model-Free),不需要环境是可导的,甚至不需要奖励函数是平滑的。
只要你能算出一个概率 π\piπ,并且能拿到一个分数 RRR,你就能优化它。这种通用性 ,是它最大的武器,也是它被称为"粗糙"的源头------因为它太通用了,以至于不依赖任何特定领域的先验知识。

第二章:被误解的"粗糙"------偏差与方差的永恒战争
为什么 REINFORCE 饱受诟病?为了理解这一点,我们需要引入统计学习中最核心的一对概念:偏差(Bias) 与 方差(Variance)。
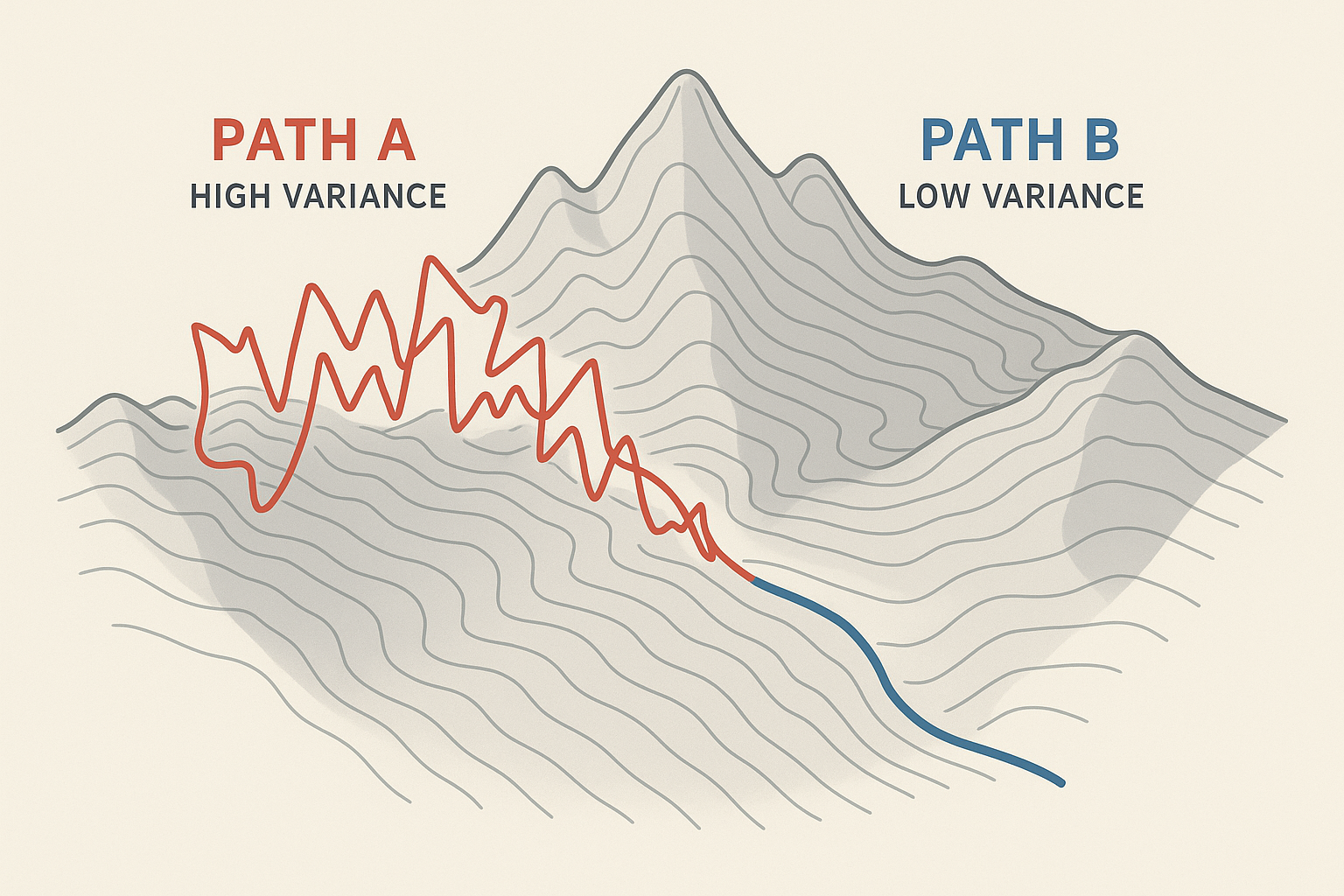
1. 蒙特卡洛的代价:高方差的噩梦
REINFORCE 是典型的蒙特卡洛(Monte Carlo)方法。这意味着它必须走完完整的一局游戏(Episode),拿到最终回报 GtG_tGt,才能回头更新参数。
想象一下你在教一个机器人走迷宫。
- 情况 A :机器人胡乱走了一通,碰巧走到了出口,得 100 分。REINFORCE 会说:"太棒了!刚才走的所有几百步都是对的,全部加强!"
- 情况 B :机器人走了同样的几百步,只是最后一步脚滑掉坑里了,得 -100 分。REINFORCE 会说:"太糟了!刚才走的所有几百步都是错的,全部抑制!"
明明中间 99% 的动作都是一样的,却因为最后的结果不同,导致梯度方向截然相反。这就是高方差。梯度的方向像醉汉一样摇摆不定,导致训练过程极度震荡,收敛极慢。
2. "粗糙"的另一面:零偏差的纯粹
然而,正是因为这种"必须走完一局"的死板,赋予了 REINFORCE 一个 Actor-Critic 无法比拟的特性:无偏估计(Unbiased Estimator)。
Actor-Critic 引入了一个 Critic(价值网络)来打分。Critic 说:"我觉得这一步值 10 分"。但 Critic 本身也是个神经网络,它刚开始也是瞎猜的。如果 Critic 猜错了(有偏差),Actor 就会跟着学坏。这就像你请了个蹩脚的教练,教练教错了,你练得越勤奋,离冠军越远。
而 REINFORCE 没有教练。它只相信残酷的现实(最终结果)。
虽然它单次更新可能很不准(方差大),但如果你给它无限的时间和采样,它的期望值是绝对指向真实梯度的(偏差为 0)。
在这个意义上,REINFORCE 不是"粗糙",它是"纯粹"。它是对梯度的真实采样,没有任何近似带来的污染。
第三章:信用分配------谁是真正的功臣?
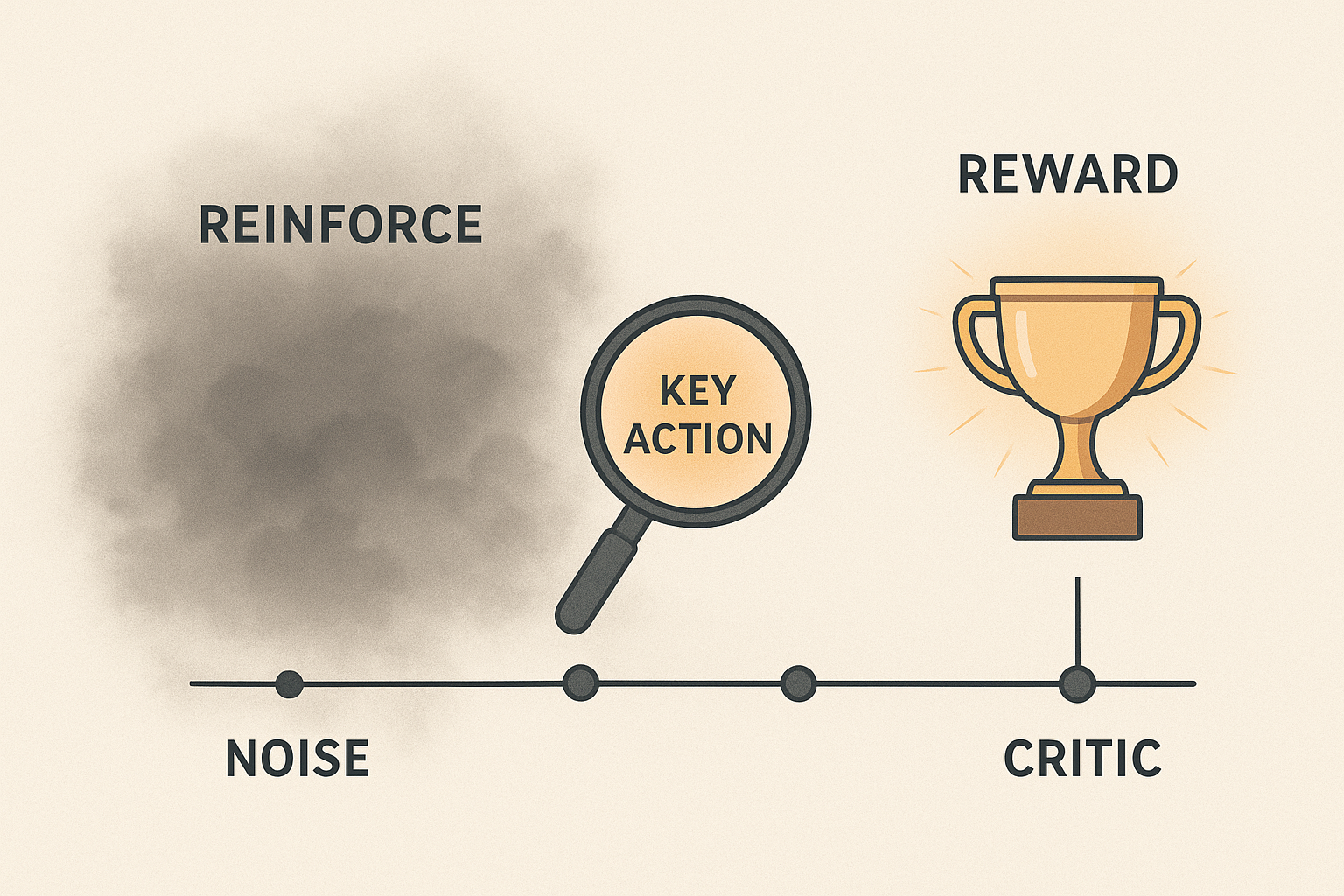
REINFORCE 的另一个痛点是 Credit Assignment(信用分配) 难题。
正如刚才的迷宫例子,如果最后赢了,REINFORCE 会倾向于奖励路径上的每一个动作。但在 100 步中,可能只有第 50 步的关键转弯决定了胜利,其他的 99 步都是在甚至可能是在"划水"或者"帮倒忙"。
基础版的 REINFORCE 确实对此无能为力。但这一问题并非 REINFORCE 的"绝症",后续的进化版本极大地缓解了这个问题:
-
引入基线(Baseline) :
我们不再看"绝对分",而是看"相对分"。Gt−b(st)G_t - b(s_t)Gt−b(st)。
如果平均分是 10 分,你拿了 20 分,只有这多出来的 10 分会贡献正向梯度。这一个简单的减法,在不引入偏差的情况下,极大地降低了方差。这就是 Vanilla Policy Gradient。
-
时间因果性(Causality) :
REINFORCE 既然是针对序列的,我们只需要让 ttt 时刻的动作对应 ttt 时刻之后的回报。未来的回报不应该影响过去的动作。这也是一种无需模型的优化手段。
尽管如此,REINFORCE 的"长序列遗忘"问题依然存在,这也是为什么在长周期任务(如星际争霸)中,一定要引入 Critic 来进行单步评估的原因。
第四章:REINFORCE 的重生------在大模型时代的逆袭
如果到这里你还认为 REINFORCE 只是历史书上的名字,那你就大错特错了。在 2023-2024 年的 AI 浪潮中,REINFORCE 的变体正站在舞台中央。
看看 ChatGPT 是怎么训练的?RLHF(Reinforcement Learning from Human Feedback)。
在 RLHF 的 PPO(Proximal Policy Optimization)阶段,本质上我们在做什么?
我们在训练一个语言模型(Actor),让它生成的每一个 Token(动作),都能获得 Reward Model 的高分。
虽然 PPO 加上了 Critic 和 Clipping(截断)机制,但其核心的梯度更新公式,依然源自策略梯度的基本逻辑。而在某些特定的文本生成场景,或者在处理**离散动作空间(Discrete Action Space)**且无法微分的环境时,纯粹的 REINFORCE 依然是首选。
为什么?
因为在自然语言生成中,Vocabulary 是离散的 。你不能输出"半个单词"。这种离散性让基于微分的方法(如重参数化技巧)变得非常复杂,而 REINFORCE 不需要对环境(词表选择)微分的特性,让它天然契合 NLP 任务。
当你听到研究人员讨论"针对大模型的直接偏好优化(DPO)"或者"自我博弈(Self-Play)"时,请记住,这些高大上算法的血管里,流淌着 REINFORCE 在 30 年前留下的血液。

结语:尊重那个"粗糙"的开创者
REINFORCE 确实是"粗糙"的。它像一把没有瞄准镜的散弹枪,全凭运气和大量的子弹(样本)来击中目标。
但也正是因为它的"粗糙",它才拥有了最强的鲁棒性 和普适性 。它不需要 Critic 的辅助,不需要环境的可微性,不需要复杂的模型假设。它只是简单地执行一条朴素的真理:
"凡是让我们成功的,就通过,凡是让我们失败的,就抑制。"
现代算法(PPO, TRPO, SAC)就像是在这把散弹枪上装了瞄准镜、减震器和激光制导。它们确实更好用了,但枪膛里的火药原理,从未改变。
所以,下一次当你写下 loss = -log_prob * reward 时,请对这个看似简单的公式保持敬畏。它不是简陋,它是大道至简。