目录
考察嵌套循环时间复杂度的分析能力,需通过循环次数推导渐近时间复杂度理解i和j循环次数与n的数学关系
考察栈在括号匹配中的实际应用,需分析字符串处理过程中栈的压入/弹出操作,判断是否因栈容是不足导致溢出
考察森林与二叉树转换的基本原理需理解转换规则及二叉树性质;同时辨析完全二叉树、分支节点等概念
[考查树结构的基本性质,需区分"分节点"与"度为 2的节点"的概念](#考查树结构的基本性质,需区分“分节点"与"度为 2的节点”的概念)
考察哈关曼树构造过程及编码长度计算,需通过频次构建最优二叉树,根据节点深度确定编码长度
考察图论基本性质(欧拉回路存在条件的变形),需通过顶点度分析路径连续性,推导回路必然存在性
[考察分块查找的效率优化原理,需理解平均查找长度与块大小的数学关系,掌握最优块大小为√n 的结论](#考察分块查找的效率优化原理,需理解平均查找长度与块大小的数学关系,掌握最优块大小为√n 的结论)
[考察B树的节点关键字数限制(4 阶 B树节点关键字数 1-3),需通过根节点与子树的关键字分布枚举所有合法结构](#考察B树的节点关键字数限制(4 阶 B树节点关键字数 1-3),需通过根节点与子树的关键字分布枚举所有合法结构)
考察线性探查与二次探查的冲突处理机制,需区分两者在"堆积现象""空闲位置查找"等方面的差异
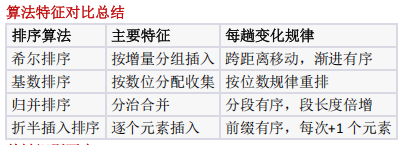
考察各排序算法的时间复杂度特性,需对比冒泡、插入、快速、选择排序在最坏情况下的移动次数差异
考察对排序算法过程的理解,需通过序列变化特征(如跳跃式移动、非局部有序)区分希尔排序与其他算法
考察考生对算法效率的敏感度,避免盲目使用暴力解法。测试对"区间极值维护"思想的应用能力,利用一次遍历替代套循环后强调对数组不标约束(i≤j)的理解,避免逻辑错误
数据结构基础概念
时间复杂度计算:重点考察嵌套循环(如双重循环的层数与变量范围)、递归算法的复杂度分析。
栈的应用:括号匹配问题中栈的操作逻辑,尤其注意栈容量限制对处理结果的影响。
二叉树存储与性质:顺序存储的规则(如节点下标与父子节点的对应关系)、完全二叉树的特征、森林与二叉树的转换规则。
算法核心考点
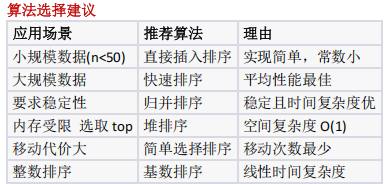
排序算法:不同排序算法的最坏情况下的比较次数、移动次数及稳定性(如简单选择排序在最坏情况下移动次数最少),希尔排序的趟数与元素位置变化特征。
查找算法:分块查找的效率优化(块大小与总元素数的平方根关系、散列表的冲突解决策略(线性探查与二次探查的区别)
树形结构算::哈夫曼编码的构造(频率与编码长度的关系)、B 树的节点关键字分布规则,
图与工程问题
图的性质:有向无环图(DAG)的拓扑排序、各顶点度与回路的关系(度乡2 的无向图必有回路)
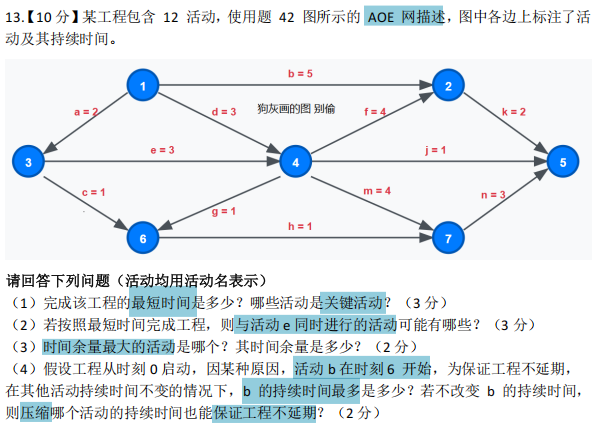
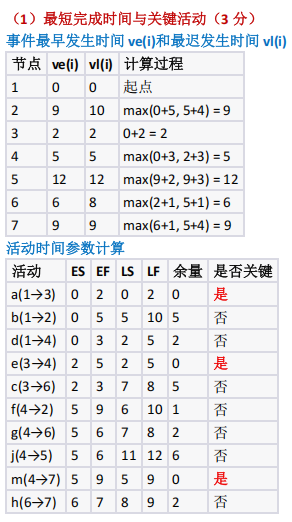
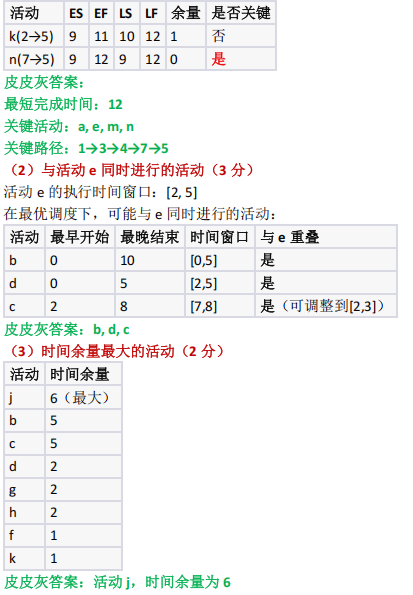
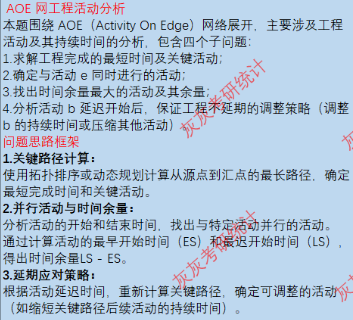
AOE 网应用:关键路径的计算(最短工程时间、关键活动识别)、活动时间余量分析、工程延期的应对策略(活动持续时间调整)
算法设计与实现
乘积最大值计算:注意元素下标约束(i≤j),避免误用排序算法优先考虑线性遍历或动态规划优化。
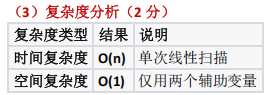
复杂度分析:算法的时间与空间复杂度计算,需与代码实现逻辑一致(如 O (n) 与 0 (n?) 的区别)
考察嵌套循环时间复杂度的分析能力,需通过循环次数推导渐近时间复杂度理解i和j循环次数与n的数学关系
下列程序段的时间复杂度是()?双重循环的套层数与循环条件的数学推导
嵌套循环的时间复 杂度计算(外层循 环为√n,内层循环 累加次数)
1.外层循环: i 从 1 到 √n ,共 √n 次;
2. 内层循环:对每个 i 执行 i 次,总次数 = 0+1+2+...+(√n-1)=√n (√n-1)/2≈n/2;
3. 忽略常数因子,时间复杂度为 O (n) ,选 B
外层循环执行 √n 次,内层循环累计执行次数约为 𝑛 2 次,因此总体复杂度为线性 O(n)
考察栈在括号匹配中的实际应用,需分析字符串处理过程中栈的压入/弹出操作,判断是否因栈容是不足导致溢出
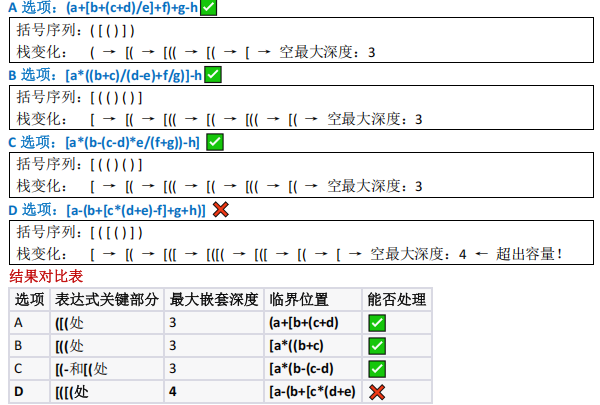
栈容量为3时,哪个括号串无法被正确匹配?
栈在括号匹配中的应用(嵌套深度限制)
- 栈容量 3 ,需判断各选项括号嵌套最大深度;
- D 选项括号序列为 [ ( [ ( ) ] ) ,遍历到 [a- (b+[c*(d+e)时,栈内有 [ ( [ ( ,深度 4 ,超出容量;
- 其他选项最大深度均为 3 ,选 D 。
本题考查的是栈容量限制下的括号匹配问题。栈的容量为 3 ,意味着在任何时刻,栈中存
储的未匹配括号数量不能超过 3 个
遍历表达式中的每个字符:
•
遇到左括号:入栈
•
遇到右括号:出栈(与栈顶左括号匹配)
•
其他字符:忽略
关键是找出栈深度的最大值,如果超过 3 则不能实现。
选项 D 在解析到 [a-(b+[c*(d+e) 时需要 4 层嵌套深度,超出了栈容量 3 的限制,因此无法实
现括号匹配
考察森林与二叉树转换的基本原理需理解转换规则及二叉树性质;同时辨析完全二叉树、分支节点等概念
下列关于二叉树及森林的叙述,正确的是?
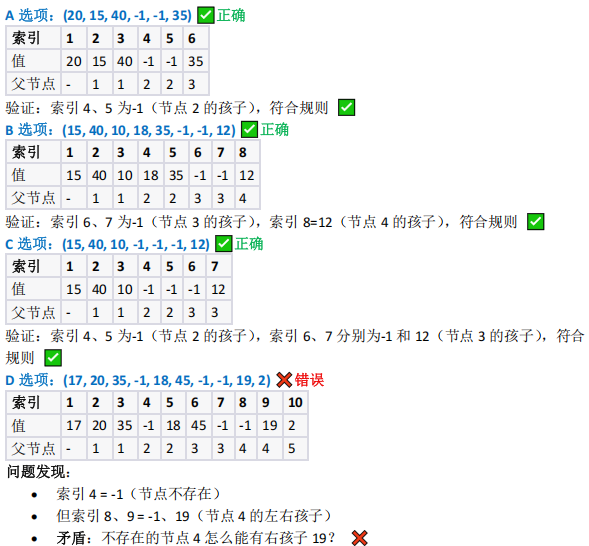
二叉树顺序存储的节点存在规则(不存在节点的子节点必为 - 1 )
- 顺序存储规则:若节点为 - 1 (不存在),其左 (2i )、右( 2i+1 )子节点必为 - 1 ;
- D 选项中,索引 4 为 - 1 ,但索引 9 ( 4 的右子节点)为 19 ,违反规则;
- 其他选项符合规则,选 D
二叉树采用顺序存储时,遵循层序遍历的索引规则:
- 根节点在索引 1(或 0)
- 对于索引为 i 的节点:
- 左孩子在索引 2
- 右孩子在索引 2i+1
关键规则 :若某节点不存在( -1 ),则其左右孩子也必须不存在
选项 D 违反了二叉树顺序存储的基本规则:索引 4 的节点不存在( -1 ),但其右孩子位置
(索引 9 )却有值 19 ,这在逻辑上是不可能的,因为不存在的节点不能有孩子节点
考查树结构的基本性质,需区分"分节点"与"度为 2的节点"的概念
完全二叉树的度特性(可能存在1个度为1的节点,如节点总数为偶数时)、二叉树性质(度为2的节点数=叶节点数-1,但分支节点包含度为1和2的节点)
二叉树与森林的性质(森林转二叉树、完全二叉树、表达式树
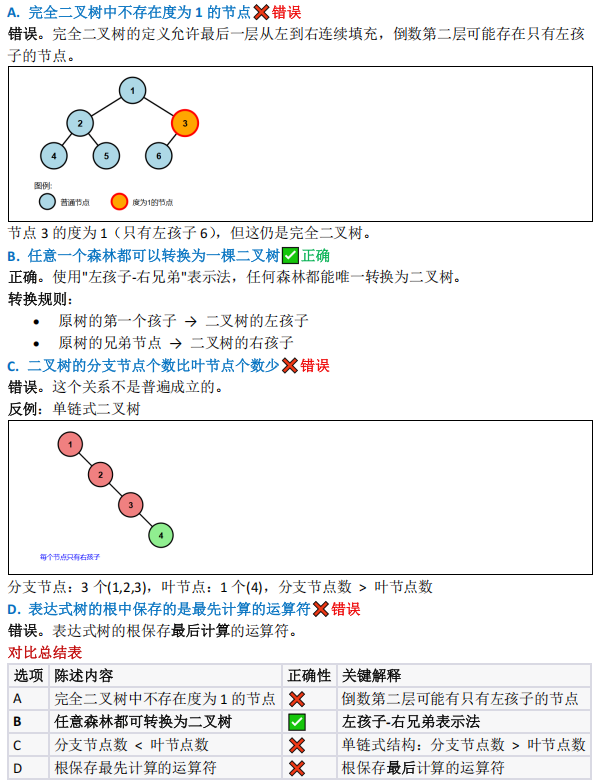
- 选项分析:
- A 错(完全二叉树可能有度 1 节点,如倒数第二层仅左孩子的节点);
- B 对(任意森林可通过 " 左孩子 - 右兄弟 " 表示法转为二叉树);
- C 错(单链二叉树分支节点数>叶节点数);
- D 错(表达式树根节点保存最后计算的运算符);
- 选 B 。
森林到二叉树的转换是数据结构中的经典算法,通过左孩子 - 右兄弟表示法可以将任意有序
森林唯一地转换为一棵二叉树
考察哈关曼树构造过程及编码长度计算,需通过频次构建最优二叉树,根据节点深度确定编码长度
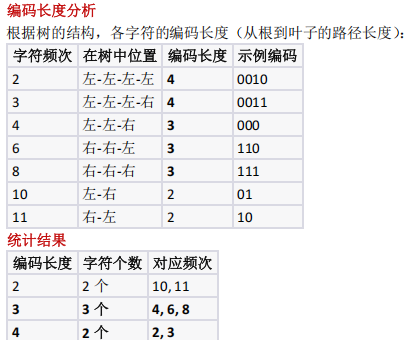
7个字符频次构造哈夫曼编码,长度>3 的字符数?
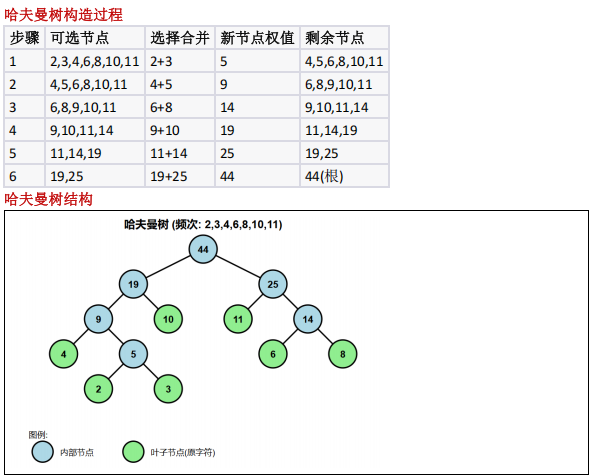
哈夫曼树构造与编码长度计算
- 7 个字符频次: 2,3,4,6,8,10,11 ,构造哈夫曼树 (每次合并最小两节点);
- 编码长度: 10 、 11 ( 2 位), 4 、 6 、 8 ( 3 位), 2、 3 ( 4 位);
- 编码长度 ≥3 的字符共 5 个,选 D 。
通过构造哈夫曼树,编码长度不小于 3 的字符有 5 个,分别是频次为 2,3,4,6,8 的字符,其
编码长度分别为 4,4,3,3,3
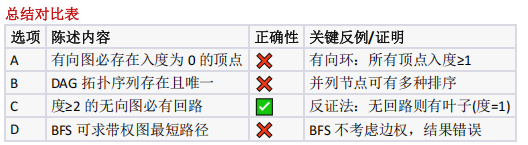
考察图论基本性质(欧拉回路存在条件的变形),需通过顶点度分析路径连续性,推导回路必然存在性
各顶点度>=2 的无向图是否必有回路?
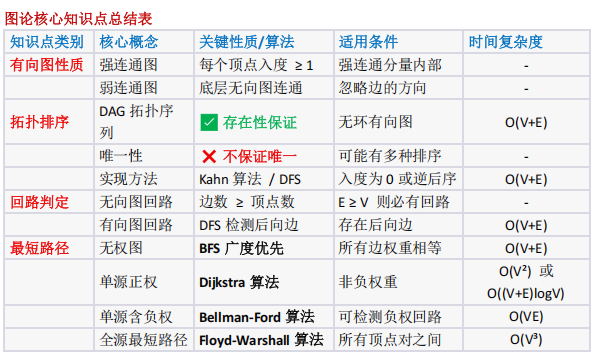
图的性质(回路判定、拓扑排序、最短路径算法适用场景)
- 选项分析:
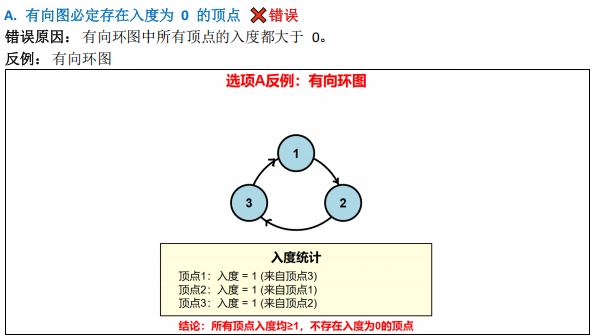
- A 错(有向环中所有节点入度 ≥1 ,无入度 0 节点);
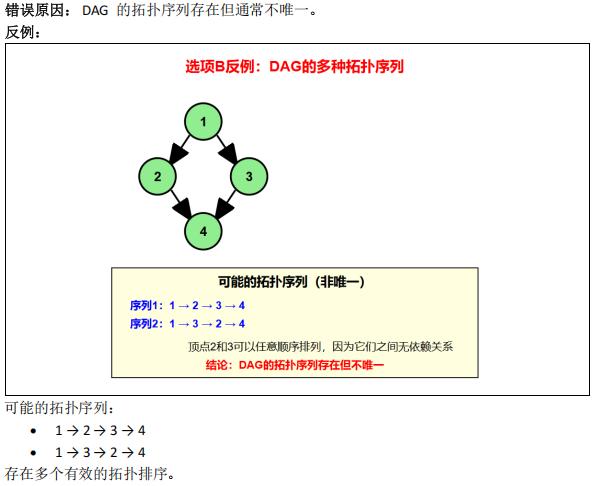
- B 错( DAG 拓扑序列存在但不唯一,如并列节点可换序);
- C 对(反证:无回路则为森林,必有叶节点(度1),与 " 度 ≥2" 矛盾);
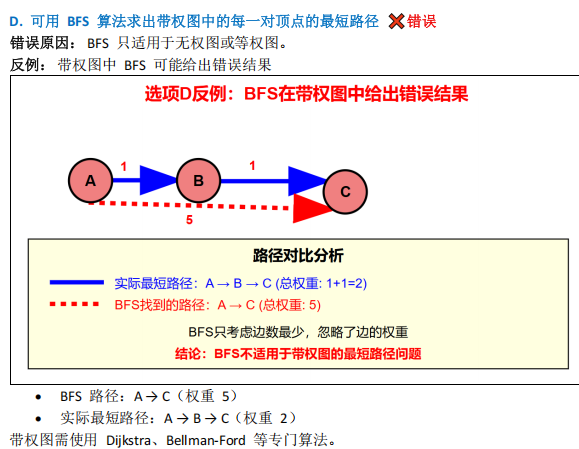
- D 错( BFS 仅适用于无权 / 等权图,带权图需Dijkstra 等算法);
- 选 C 。
考察分块查找的效率优化原理,需理解平均查找长度与块大小的数学关系,掌握最优块大小为√n 的结论
400个元素分块查找,每块多少个效率最高
分块查找的平均查 找长度最优化(最优块大小计算)
- 分块查找平均查找长度 ASL=(m+1)/2+(k+1)/2 ,其中 m = 块数, k = 每块元素数, n=mk ;
- 最优化条件: m=k=√n , n=400→√400=20 ;
- 每块最优元素数为 20 ,选 C 。
考察B树的节点关键字数限制(4 阶 B树节点关键字数 1-3),需通过根节点与子树的关键字分布枚举所有合法结构
7个关键字的 4阶 B树有多少种可能结构?
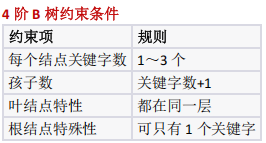
4 阶 B 树的结构约束与不同高度的数量计算(关键字数 1~3 ,叶节点同层)
- 4 阶 B 树规则:每个节点关键字 1~3 个,叶节点同层;
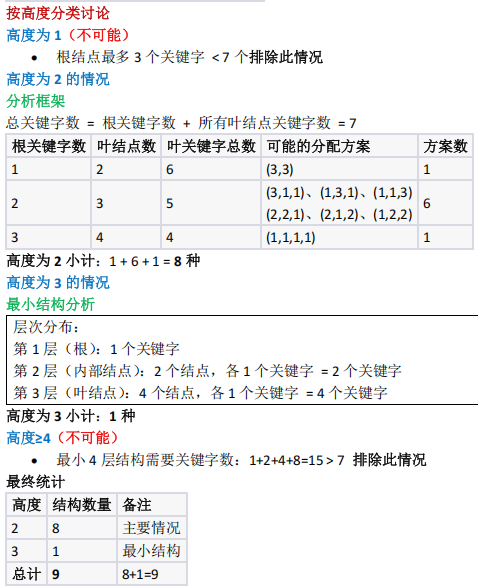
- 7 个关键字:
- 高度 2 : 8 种(根 1 个关键字 + 叶 2 块 6 个 / 根 2 个 + 叶 3 块 5 个 / 根 3 个 + 叶 4 块 4 个);
- 高度 3 : 1 种(根 1 + 中层 2 个 + 叶 4 个, 共 1+2+4=7 );
- 总计 9 种,选 C 。
- 分层思考 :根据 B 树高度分类讨论
- 约束检验 :每层关键字数量必须符合 4 阶 B 树规则
- 穷举验证 :逐一验证每种可能的关键字分配
- 边界情况 :注意最小和最大高度的限制
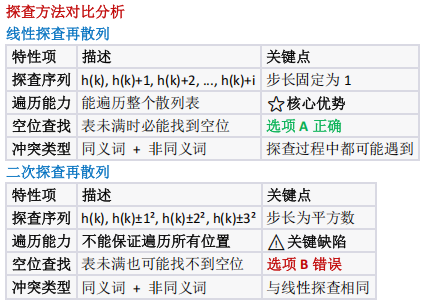
考察线性探查与二次探查的冲突处理机制,需区分两者在"堆积现象""空闲位置查找"等方面的差异
下列关于散列表的说法,正确的是?
散列冲突处理(线 性探查与二次探查 的特性对比)
- 选项分析:
- A 对(线性探查步长 1 ,可遍历全表,表不满必找空位);
- B 错(二次探查步长为平方数,无法遍历全表,表不满也可能找不到空位);
- C 错(线性探查会处理非同义词冲突,如探查时碰撞已占用非同义词位置);
- D 错(二次探查也会处理同义词冲突,如两关键字散列地址相同);
- 选 A 。
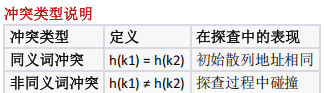
重要结论 :无论线性探查还是二次探查,都可能处理两种类型的冲突
关键知识点
1. 遍历完整性
- 线性探查:步长为 1,能遍历所有位置
- 二次探查:步长为平方数,通常只能遍历部分位置
2. 空位查找保证
- 线性探查:表未满 ⇒ 必能找到空位
- 二次探查:表未满 ⇏ 必能找到空位
3. 冲突处理范围
两种方法都处理:同义词冲突 + 非同义词冲突
考察各排序算法的时间复杂度特性,需对比冒泡、插入、快速、选择排序在最坏情况下的移动次数差异
哪种排序在最坏情况下移动次数最少?
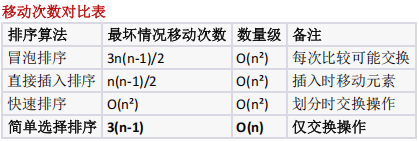
各排序算法最坏情况下的元素移动次数对比
- 移动次数分析:
- 冒泡排序: 3n (n-1)/2 ( O (n²) );
- 直接插入排序: n (n-1)/2 ( O (n²) );
- 快速排序: O (n²) ;
- 简单选择排序: 3 (n-1) ( O (n) ,仅交换 n-1 次,每次 3 次移动);
- 最坏移动最少的是简单选择排序,选 D 。
各排序算法分析
1. 冒泡排序
最坏情况 :序列完全逆序
移动次数 : 3n(n-1)/2
原理 :相邻元素两两比较交换,每次交换需要 3 次移动操作
2. 直接插入排序
最坏情况 :序列完全逆序
移动次数 : n(n-1)/2
原理 :每次插入都需要移动已排序部分的所有元素
3. 快速排序
最坏情况 :序列已有序或每次基准选择最值
移动次数 : O(n²) 级别
原理 :划分过程中的元素交换,移动次数与比较次数同数量级
4. 简单选择排序
最坏情况 :任意初始序列
移动次数 : 3(n-1)
原理 :每次只需交换一次(选中的最值与当前位置),每次交换 3 次移动
简单选择排序在最坏情况下移动次数最少,仅为 3(n-1) 次,呈线性关系。这是因为:
- 固定交换次数 :无论初始序列如何,都只需要 n-1 次交换
- 每次交换固定移动 :每次交换恰好需要 3 次移动操作
- 与数据分布无关 :移动次数不受初始序列排列影响
相比之下,其他三种算法在最坏情况下的移动次数都是 O(n²) 级别,远大于简单选择排序的
O(n) 级别
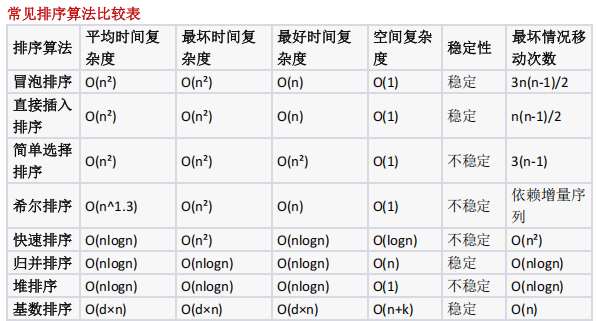
- 移动次数最少:简单选择排序 - 3(n-1)次
- 比较次数最少:归并排序 - nlogn 次
- 最稳定高效:归并排序 - 任何情况下 O(nlogn)
- 平均最快:快速排序 - 实际应用中表现最佳
- 原地排序:除归并排序外,其他主要算法都是原地排序
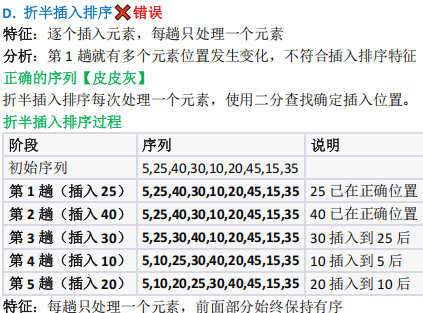
考察对排序算法过程的理解,需通过序列变化特征(如跳跃式移动、非局部有序)区分希尔排序与其他算法
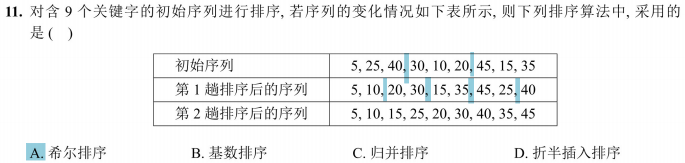
根据两趟排序结果判断算法类型A希尔排序B 基数数排序C 归并排序D 折半插入排序
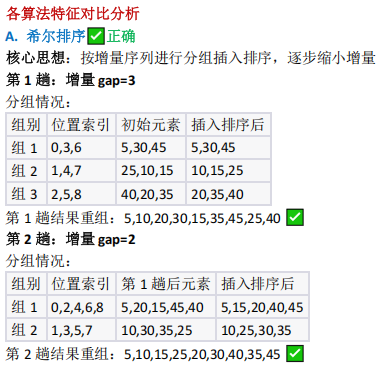
排序算法识别(希尔排序的分组插入特征)
- 希尔排序按增量分组插入,第 1 趟增量gap=3,分组为 (0,3,6) 、 (1,4,7) 、 (2,5,8) ,排序后
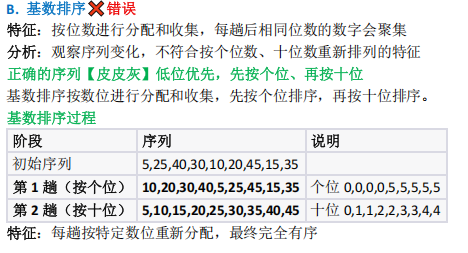
重组为第 1 趟序列;第 2 趟增量 gap=2 ,分组后排序得第 2 趟序列,与题目一致;- 基数排序(按数位)、归并排序(分段有序)、折半插入排序(前缀有序)均不匹配,选 A 。
希尔排序识别特征
• ✓ 多个元素同时大幅移动
• ✓ 不是完全按大小顺序调整
• ✓ 体现分组处理特点
其他算法识别特征
• 基数排序:严格按数位规律排列
• 归并排序:明显的分段有序特征
• 折半插入排序:每趟仅一个元素位置改变
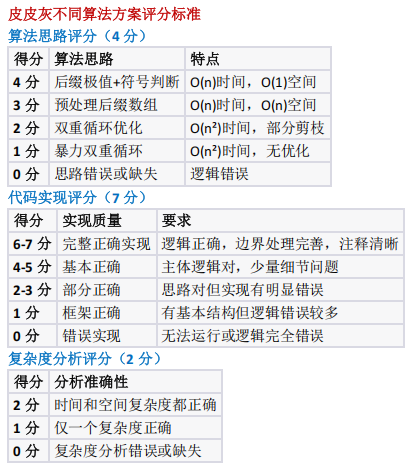
考察考生对算法效率的敏感度,避免盲目使用暴力解法。测试对"区间极值维护"思想的应用能力,利用一次遍历替代套循环后强调对数组不标约束(i≤j)的理解,避免逻辑错误
考察关楗路径算法的应用
:通过计算最长路径确定最短工期,识别关键活动,检验对 AOE网核心概念的理解;考查活动时间关系分析能为:通过分析活动时间区间的重叠性,判断并行活动,强化对工程时序的理解;考查时间余量的计算与应用:通过比较各活动的LS-ES,确定可延迟的活动,理解非关键活动的灵活性;考查工程优化与问题解决能力:结合活动延迟场景,分析调整略(调整自身持续时间或压缩其他活动)