【题目来源】
https://oj.czos.cn/p/2190
【题目描述】
给定一颗树,树中有 n 个结点(编号1~n)。请你找到树的重心,并输出树的重心的结点编号。
重心定义:++重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中结点数的最大值最小,那么这个结点被称为树的重心++ 。
如下图所示的树的重心为1号结点。
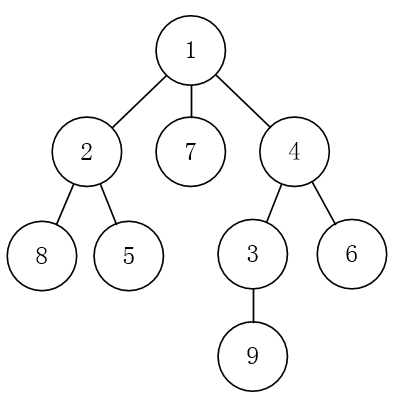
【输入格式】
第 1 行读入一个整数 n,代表树的结点的数量(1≤n≤10^5);
接下来 n-1 行,每行读入两个整数 x 和 y,表示结点 x 和 y 之间有一条边(注意:不确定 x 和 y 的父子关系)。
【输出格式】
请输出树的重心的结点编号,如果树有多个重心,请按照编号从小到大依次输出,数字之间用空格隔开。
【输入样例一】
6
1 2
1 3
2 4
3 5
5 6
【输出样例一】
1 3
【输入样例二】
8
1 2
1 3
2 4
3 5
5 6
5 7
5 8
【输出样例二】
3 5
【数据范围】
1≤n≤10^5
【算法分析】
依据样例二,绘制树的示意图,然后依据定义分析"树的重心"过程如下。
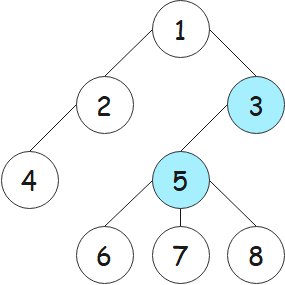
删除结点 1,产生的两个连通块中结点数分别为 2、5,最大值为 5;
删除结点 2,产生的两个连通块中结点数分别为 1、6,最大值为 6;
删除结点 3,产生的两个连通块中结点数分别为 3、4,最大值为 4;
删除结点 4,产生的一个连通块中结点数分别为 7,最大值为 7;
删除结点 5,产生的四个连通块中结点数分别为 1、1、1、4,最大值为 4;
删除结点 6,产生的一个连通块中结点数分别为 7,最大值为 7;
删除结点 7,产生的一个连通块中结点数分别为 7,最大值为 7;
删除结点 8,产生的一个连通块中结点数分别为 7,最大值为 7。
综上,可知 8 个最大值中的最小值为 4,但有两个。也就是说,给出的树有两个重心,分别为结点 3、结点 5。
【算法代码一:邻接表】
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
vector<int> g[N];
int cnt[N],dis[N];
int n,cr; //core
int imin=INT_MAX;
void dfs(int u,int fa) {
cnt[u]=1;
int rem=0; //remnant
for(int i=0; i<g[u].size(); i++) {
int j=g[u][i];
if(j==fa) continue;
dfs(j,u);
cnt[u]+=cnt[j];
rem=max(rem,cnt[j]);
}
rem=max(rem,n-cnt[u]);
dis[u]=rem;
if(rem<imin || rem==imin && u<cr) {
imin=rem;
cr=u;
}
}
int main() {
cin>>n;
int a,b;
for(int i=1; i<n; i++) {
cin>>a>>b;
g[a].push_back(b);
g[b].push_back(a);
}
dfs(1,-1);
for(int i=1; i<=n; i++) {
if(imin==dis[i]) {
cout<<i<<" ";
}
}
return 0;
}
/*
in:
6
1 2
1 3
2 4
3 5
5 6
out:
1 3
*/【算法代码二:链式前向星】
cnt[u] 记录以节点 u 为根的子树中所有节点的数量(包括 u 本身)。
dis[u] 记录以 u 作为重心时的最大子树节点数。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int M=N<<1;
int h[N],e[M],ne[M],idx;
int cnt[N],dis[N];
int n,cr; //core
int imin=INT_MAX;
void add(int a,int b) {
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa) {
cnt[u]=1;
int rem=0; //remnant
for(int i=h[u]; i!=-1; i=ne[i]) {
int j=e[i];
if(j==fa) continue;
dfs(j,u);
cnt[u]+=cnt[j];
rem=max(rem,cnt[j]);
}
rem=max(rem,n-cnt[u]);
dis[u]=rem;
if(rem<imin || rem==imin && u<cr) {
imin=rem;
cr=u;
}
}
int main() {
memset(h,-1,sizeof h);
cin>>n;
for(int i=1; i<n; i++) {
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1,-1);
for(int i=1; i<=n; i++) {
if(imin==dis[i]) {
cout<<i<<" ";
}
}
return 0;
}
/*
in:
6
1 2
1 3
2 4
3 5
5 6
out:
1 3
*/【参考文献】
https://www.cnblogs.com/triwa/p/19341989
https://blog.csdn.net/hnjzsyjyj/article/details/119912125
https://blog.csdn.net/weixin_43810158/article/details/88391828
https://blog.csdn.net/weixin_73739312/article/details/129072527