【张量等变学习】张量学习与正交，洛伦兹和辛对称

deardao2025-12-17 8:13

目录

一、研究背景与意义

  1. 张量的重要性：张量是众多科学领域（时间序列分析、材料科学、物理学、理论计算机科学等）的基础数据结构。例如，在自然科学中，张量值数据可用于表示极化、渗透率和应力；在理论计算机科学中，涉及张量分解、种植张量模型等问题；在时间序列分析中，路径签名能将路径数据转化为张量序列，实现对重参数化不变的时间序列处理。

  2. 对称性的关键作用：在物理学中，张量不仅是多维数值数组，还具有特定的坐标变换性质，张量函数需遵循由群作用定义的不变性或等变性规则。利用这些对称性可优化机器学习模型，提升其在相关领域问题中的性能。

  3. 研究缺口：现有研究虽在机器学习模型中融入对称性和结构约束，但缺乏针对张量的通用等变机器学习框架，无法同时适配正交群、洛伦兹群、辛群等经典李群的对角作用。

    论文：Causal Structure Learning in Hawkes Processes with Complex Latent Confounder Networks
    地址：https://openreview.net/pdf?id=1FCZ4f8dAY

请各位同学给我点赞，激励我创作更好、更多、更优质的内容！^_^

关注微信公众号 ，获取更多资讯

二、核心概念定义

1. 张量相关定义

  • k ( p ) k_{(p)} k(p)-张量 ： 1 ( p ) 1_{(p)} 1(p)-张量空间为配备 O ( d ) O(d) O(d)作用的 R d \mathbb{R}^d Rd， k ( p ) k_{(p)} k(p)-张量由 k k k个 1 ( p i ) 1_{(p_i)} 1(pi)-张量的外积生成（ p = ∏ i = 1 k p i p=\prod_{i=1}^k p_i p=∏i=1kpi）， O ( d ) O(d) O(d)作用为对角作用， T k ( R d , p ) T_k(\mathbb{R}^d,p) Tk(Rd,p)表示 d d d维 k ( p ) k_{(p)} k(p)-张量空间（ p = + 1 p=+1 p=+1为向量空间， p = − 1 p=-1 p=−1为伪向量空间）。
  • 爱因斯坦求和符号 ：用于表示张量积，重复索引表示求和，非重复索引保留在结果中，例如矩阵乘积 [ a b ] i , j = [ a ] i , ℓ [ b ] ℓ , j : = ∑ ℓ = 1 d [ a ] i , ℓ [ b ] ℓ , j [ab]{i,j}=[a]{i,\ell}[b]{\ell,j}:=\sum{\ell=1}^d[a]{i,\ell}[b]{\ell,j} [ab]i,j=[a]i,ℓ[b]ℓ,j:=∑ℓ=1d[a]i,ℓ[b]ℓ,j。
  • 外积 ：给定 a ∈ T k ( R d , p ) a \in T_k(\mathbb{R}^d,p) a∈Tk(Rd,p)和 b ∈ T k ′ ( R d , p ′ ) b \in T_{k'}(\mathbb{R}^d,p') b∈Tk′(Rd,p′)，外积 a ⊗ b ∈ T k + k ′ ( R d , p p ′ ) a \otimes b \in T_{k+k'}(\mathbb{R}^d,pp') a⊗b∈Tk+k′(Rd,pp′)，定义为 [ a ⊗ b ] i 1 , . . . , i k + k ′ = [ a ] i 1 , . . . , i k [ b ] i k + 1 , . . . , i k + k ′ [a \otimes b]{i_1,...,i{k+k'}}=[a]{i_1,...,i_k}[b]{i_{k+1},...,i_{k+k'}} [a⊗b]i1,...,ik+k′=[a]i1,...,ik[b]ik+1,...,ik+k′。
  • k k k-收缩 ：对 a ∈ T 2 k + k ′ ( R d , p ) a \in T_{2k+k'}(\mathbb{R}^d,p) a∈T2k+k′(Rd,p)， k k k-收缩 ι k ( a ) ∈ T k ′ ( R d , p ) \iota_k(a) \in T_{k'}(\mathbb{R}^d,p) ιk(a)∈Tk′(Rd,p)，定义为 [ ι k ( a ) ] j 1 , . . . , j k ′ : = [ a ] i 1 , . . . , i k , i 1 , . . . , i k , j 1 , . . . , j k ′ [\iota_k(a)]{j_1,...,j{k'}}:=[a]{i_1,...,i_k,i_1,...,i_k,j_1,...,j{k'}} [ιk(a)]j1,...,jk′:=[a]i1,...,ik,i1,...,ik,j1,...,jk′。
  • 张量索引置换 ：对 a ∈ T k ( R d , p ) a \in T_k(\mathbb{R}^d,p) a∈Tk(Rd,p)和置换 σ ∈ S k \sigma \in S_k σ∈Sk，置换后张量 a σ a^\sigma aσ定义为 [ a σ ] i 1 , . . . , i k : = [ a ] i σ − 1 ( 1 ) , . . . , i σ − 1 ( k ) [a^\sigma]{i_1,...,i_k}:=[a]{i_{\sigma^{-1}(1)},...,i_{\sigma^{-1}(k)}} [aσ]i1,...,ik:=[a]iσ−1(1),...,iσ−1(k)。

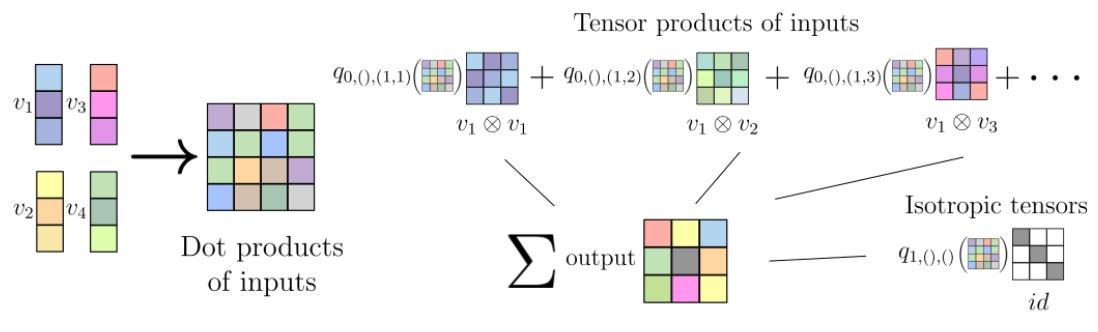
图1：推论1中4个输入向量在 R 3 R^{3} R3和一个 2 ( + ) 2_{(+)} 2(+)张量输出的方法说明。输入的张量积包括输入向量的有序对的所有16个可能的张量积，加上各向同性的Kronecker delta，标记为 i d . id. id.这里显示的系数 q t , σ , J qt, \sigma, J qt,σ,J使用 σ = 0 \sigma=0 σ=0中的单位置换 S k ′ S_{k'} Sk′。

一、研究背景与意义

  1. 张量的重要性：张量是众多科学领域（时间序列分析、材料科学、物理学、理论计算机科学等）的基础数据结构。例如，在自然科学中，张量值数据可用于表示极化、渗透率和应力；在理论计算机科学中，涉及张量分解、种植张量模型等问题；在时间序列分析中，路径签名能将路径数据转化为张量序列，实现对重参数化不变的时间序列处理。
  2. 对称性的关键作用：在物理学中，张量不仅是多维数值数组，还具有特定的坐标变换性质，张量函数需遵循由群作用定义的不变性或等变性规则。利用这些对称性可优化机器学习模型，提升其在相关领域问题中的性能。
  3. 研究缺口：现有研究虽在机器学习模型中融入对称性和结构约束，但缺乏针对张量的通用等变机器学习框架，无法同时适配正交群、洛伦兹群、辛群等经典李群的对角作用。

2. 不变性与等变性

  • 不变函数 ： f : T k ( R d , p ) → T k ′ ( R d , p ′ ) f:T_k(\mathbb{R}^d,p) \to T_{k'}(\mathbb{R}^d,p') f:Tk(Rd,p)→Tk′(Rd,p′)满足 f ( g ⋅ a ) = f ( a ) f(g \cdot a)=f(a) f(g⋅a)=f(a)（对所有 g ∈ O ( d ) g \in O(d) g∈O(d)）。
  • 等变函数 ： f : T k ( R d , p ) → T k ′ ( R d , p ′ ) f:T_k(\mathbb{R}^d,p) \to T_{k'}(\mathbb{R}^d,p') f:Tk(Rd,p)→Tk′(Rd,p′)满足 f ( g ⋅ a ) = g ⋅ f ( a ) f(g \cdot a)=g \cdot f(a) f(g⋅a)=g⋅f(a)（对所有 g ∈ O ( d ) g \in O(d) g∈O(d)），多输入函数中同一群元素作用于所有输入。

3. 各向同性张量与特殊张量

  • 各向同性张量 ： a ∈ T k ( R d , p ) a \in T_k(\mathbb{R}^d,p) a∈Tk(Rd,p)满足 g ⋅ a = a g \cdot a=a g⋅a=a（对所有 g ∈ O ( d ) g \in O(d) g∈O(d)）。
  • 克罗内克delta（ δ \delta δ） ： O ( d ) O(d) O(d)-各向同性 2 ( + ) 2_{(+)} 2(+)-张量， [ δ ] i j = 1 [\delta]_{ij}=1 [δ]ij=1（ i = j i=j i=j），否则为0，对应单位矩阵 I d \mathbb{I}_d Id。
  • 列维-奇维塔符号（ ϵ \epsilon ϵ） ： d ≥ 2 d \geq 2 d≥2时， O ( d ) O(d) O(d)-各向同性 d ( − ) d_{(-)} d(−)-张量，索引全不同时为排列奇偶性（偶为1，奇为-1），否则为0。

4. 关键群定义

  • 正交群（ O ( d ) O(d) O(d)） ：欧氏空间 R d \mathbb{R}^d Rd中固定原点的等距变换群，满足 M ( g ) ⊤ M ( g ) = I d M(g)^\top M(g)=\mathbb{I}_d M(g)⊤M(g)=Id。
  • 不定正交群（ O ( s , d − s ) O(s,d-s) O(s,d−s)） ：保持闵可夫斯基内积 < u , v > s = u ⊤ I s , d − s v <u,v>s=u^\top \mathbb{I}{s,d-s}v <u,v>s=u⊤Is,d−sv的线性变换群，包含洛伦兹群（ d = 4 , s ∈ { 1 , 3 } d=4,s \in \{1,3\} d=4,s∈{1,3}时）。
  • 辛群（ S p ( d ) Sp(d) Sp(d)） ： d d d为偶数时，保持辛积 < u , v > s y m p = u ⊤ J d v <u,v>{symp}=u^\top J_d v <u,v>symp=u⊤Jdv的线性变换群， J d = ( − I d / 2 I d / 2 ) J_d=\begin{pmatrix}-\mathbb{I}{d/2}&\mathbb{I}_{d/2}\end{pmatrix} Jd=(−Id/2Id/2)。

三、核心理论成果

1. 正交群等变多项式函数（ O ( d ) O(d) O(d)-Equivariant Polynomials）

定理1（ O ( d ) O(d) O(d)-等变多项式函数表征）

设 f : ∏ i = 1 n T k i ( R d , p i ) → T k ′ ( R d , p ′ ) f:\prod_{i=1}^n T_{k_i}(\mathbb{R}^d,p_i) \to T_{k'}(\mathbb{R}^d,p') f:∏i=1nTki(Rd,pi)→Tk′(Rd,p′)为次数不超过 R R R的 O ( d ) O(d) O(d)-等变多项式函数，则可表示为：
f ( a 1 , . . . , a n ) = ∑ r = 0 R ∑ 1 ≤ ℓ 1 ≤ ⋯ ≤ ℓ r ≤ n ι k ℓ 1 , . . . , ℓ r ( a ℓ 1 ⊗ ⋯ ⊗ a ℓ r ⊗ c ℓ 1 , . . . , ℓ r ) f(a_1,...,a_n)=\sum_{r=0}^R \sum_{1 \leq \ell_1 \leq \cdots \leq \ell_r \leq n} \iota_{k_{\ell_1,...,\ell_r}}(a_{\ell_1} \otimes \cdots \otimes a_{\ell_r} \otimes c_{\ell_1,...,\ell_r}) f(a1,...,an)=r=0∑R1≤ℓ1≤⋯≤ℓr≤n∑ιkℓ1,...,ℓr(aℓ1⊗⋯⊗aℓr⊗cℓ1,...,ℓr)

其中， c ℓ 1 , . . . , ℓ r c_{\ell_1,...,\ell_r} cℓ1,...,ℓr为 O ( d ) O(d) O(d)-各向同性 ( k ℓ 1 , . . . , ℓ r + k ′ ) ( p ℓ 1 , . . . , ℓ r p ′ ) (k_{\ell_1,...,\ell_r}+k'){(p{\ell_1,...,\ell_r}p')} (kℓ1,...,ℓr+k′)(pℓ1,...,ℓrp′)-张量， k ℓ 1 , . . . , ℓ r = ∑ q = 1 r k ℓ q k_{\ell_1,...,\ell_r}=\sum_{q=1}^r k_{\ell_q} kℓ1,...,ℓr=∑q=1rkℓq， p ℓ 1 , . . . , ℓ r = ∏ q = 1 r p ℓ q p_{\ell_1,...,\ell_r}=\prod_{q=1}^r p_{\ell_q} pℓ1,...,ℓr=∏q=1rpℓq。

推论1（输入为向量的 O ( d ) O(d) O(d)-等变多项式）

设 f : ∏ i = 1 n T 1 ( R d , + ) → T k ′ ( R d , + ) f:\prod_{i=1}^n T_1(\mathbb{R}^d,+) \to T_{k'}(\mathbb{R}^d,+) f:∏i=1nT1(Rd,+)→Tk′(Rd,+)为 O ( d ) O(d) O(d)-等变多项式函数，则可表示为：
f ( v 1 , . . . , v n ) = ∑ t = 0 ⌊ k ′ 2 ⌋ ∑ σ ∈ S k ′ ∑ 1 ≤ J 1 ≤ ⋯ ≤ J k ′ − 2 t ≤ n q t , σ , J ( ( < v i , v j > ) i , j = 1 n ) ( v J 1 ⊗ ⋯ ⊗ v J k ′ − 2 t ⊗ δ ⊗ t ) σ f(v_1,...,v_n)=\sum_{t=0}^{\lfloor \frac{k'}{2} \rfloor} \sum_{\sigma \in S_{k'}} \sum_{1 \leq J_1 \leq \cdots \leq J_{k'-2t} \leq n} q_{t,\sigma,J}((<v_i,v_j>){i,j=1}^n)(v{J_1} \otimes \cdots \otimes v_{J_{k'-2t}} \otimes \delta^{\otimes t})^\sigma f(v1,...,vn)=t=0∑⌊2k′⌋σ∈Sk′∑1≤J1≤⋯≤Jk′−2t≤n∑qt,σ,J((<vi,vj>)i,j=1n)(vJ1⊗⋯⊗vJk′−2t⊗δ⊗t)σ

其中， q t , σ , J q_{t,\sigma,J} qt,σ,J为输入向量内积的多项式， σ \sigma σ为索引置换， J J J为输入张量索引。

推论2（对称 2 ( + ) 2_{(+)} 2(+)-张量输入输出的 O ( d ) O(d) O(d)-等变函数）

设 f : T 2 s y m ( R d , + ) → T 2 s y m ( R d , + ) f:T_2^{sym}(\mathbb{R}^d,+) \to T_2^{sym}(\mathbb{R}^d,+) f:T2sym(Rd,+)→T2sym(Rd,+)为 O ( d ) O(d) O(d)-等变函数，则存在置换等变函数 f ~ : R d i a g d × d → R d i a g d × d \tilde{f}:\mathbb{R}{diag}^{d \times d} \to \mathbb{R}{diag}^{d \times d} f~:Rdiagd×d→Rdiagd×d，对所有 A ∈ T 2 s y m ( R d , + ) A \in T_2^{sym}(\mathbb{R}^d,+) A∈T2sym(Rd,+)（ A = Q Λ Q ⊤ A=Q\Lambda Q^\top A=QΛQ⊤为特征值分解），有 f ( A ) = Q f ~ ( Λ ) Q ⊤ f(A)=Q\tilde{f}(\Lambda)Q^\top f(A)=Qf~(Λ)Q⊤。

2. 其他群的推广（洛伦兹群、辛群）

定理2（ O ( s , d − s ) O(s,d-s) O(s,d−s)或 S p ( d ) Sp(d) Sp(d)-等变全纯函数）

设 G G G为 O ( s , d − s ) O(s,d-s) O(s,d−s)或 S p ( d ) Sp(d) Sp(d)， f : ∏ i = 1 n T k i ( R d , χ i ) → T k ′ ( R d , χ ′ ) f:\prod_{i=1}^n T_{k_i}(\mathbb{R}^d,\chi_i) \to T_{k'}(\mathbb{R}^d,\chi') f:∏i=1nTki(Rd,χi)→Tk′(Rd,χ′)为 G G G-等变全纯函数，则可表示为：
f ( a 1 , . . . , a n ) = ∑ r = 0 ∞ ∑ 1 ≤ ℓ 1 ≤ ⋯ ≤ ℓ r ≤ n ι k ℓ 1 , . . . , ℓ r G ( a ℓ 1 ⊗ ⋯ ⊗ a ℓ r ⊗ c ℓ 1 , . . . , ℓ r ) f(a_1,...,a_n)=\sum_{r=0}^\infty \sum_{1 \leq \ell_1 \leq \cdots \leq \ell_r \leq n} \iota_{k_{\ell_1,...,\ell_r}}^G(a_{\ell_1} \otimes \cdots \otimes a_{\ell_r} \otimes c_{\ell_1,...,\ell_r}) f(a1,...,an)=r=0∑∞1≤ℓ1≤⋯≤ℓr≤n∑ιkℓ1,...,ℓrG(aℓ1⊗⋯⊗aℓr⊗cℓ1,...,ℓr)

其中， c ℓ 1 , . . . , ℓ r c_{\ell_1,...,\ell_r} cℓ1,...,ℓr为 G G G-各向同性张量， ι k G \iota_k^G ιkG为 G G G-等变收缩（ O ( s , d − s ) O(s,d-s) O(s,d−s)用 I s , d − s \mathbb{I}_{s,d-s} Is,d−s， S p ( d ) Sp(d) Sp(d)用 J d J_d Jd）。

推论3（输入为向量的 G G G-等变全纯函数）

设 G G G为 O ( s , d − s ) O(s,d-s) O(s,d−s)或 S p ( d ) Sp(d) Sp(d)， f : ∏ i = 1 n T 1 ( R d , χ 0 ) → T k ( R d , χ 0 ) f:\prod_{i=1}^n T_1(\mathbb{R}^d,\chi_0) \to T_k(\mathbb{R}^d,\chi_0) f:∏i=1nT1(Rd,χ0)→Tk(Rd,χ0)（ χ 0 \chi_0 χ0为常值映射1）为 G G G-等变全纯函数，则可表示为：
f ( v 1 , . . . , v n ) = ∑ t = 0 ⌊ k 2 ⌋ ∑ σ ∈ S k ∑ 1 ≤ J 1 ≤ ⋯ ≤ J k − 2 t ≤ n q t , σ , J ( ( < v i , v j > G ) i , j = 1 n ) ( v J 1 ⊗ ⋯ ⊗ v J k − 2 t ⊗ θ G ⊗ t ) σ f(v_1,...,v_n)=\sum_{t=0}^{\lfloor \frac{k}{2} \rfloor} \sum_{\sigma \in S_k} \sum_{1 \leq J_1 \leq \cdots \leq J_{k-2t} \leq n} q_{t,\sigma,J}((<v_i,v_j>G){i,j=1}^n)(v_{J_1} \otimes \cdots \otimes v_{J_{k-2t}} \otimes \theta_G^{\otimes t})^\sigma f(v1,...,vn)=t=0∑⌊2k⌋σ∈Sk∑1≤J1≤⋯≤Jk−2t≤n∑qt,σ,J((<vi,vj>G)i,j=1n)(vJ1⊗⋯⊗vJk−2t⊗θG⊗t)σ

其中， < ⋅ , ⋅ > G <\cdot,\cdot>G <⋅,⋅>G为 G G G对应的双线性积（ O ( s , d − s ) O(s,d-s) O(s,d−s)用 < ⋅ , ⋅ > s <\cdot,\cdot>s <⋅,⋅>s， S p ( d ) Sp(d) Sp(d)用 < ⋅ , ⋅ > s y m p <\cdot,\cdot>{symp} <⋅,⋅>symp）， θ G \theta_G θG为对应张量（ O ( s , d − s ) O(s,d-s) O(s,d−s)用 I s , d − s \mathbb{I}{s,d-s} Is,d−s， S p ( d ) Sp(d) Sp(d)用 J d J_d Jd）。

四、实验验证

1. 应力-应变张量（材料科学）

  • 问题 ：学习 O ( d ) O(d) O(d)-各向同性neo-Hookean超弹性材料的二阶应力张量（ S S S）与应变张量（ C C C）关系， S = ( 1 2 λ log ⁡ det ⁡ C − μ ) C − 1 + μ I d S=(\frac{1}{2}\lambda \log \det C - \mu)C^{-1}+\mu \mathbb{I}_d S=(21λlogdetC−μ)C−1+μId（ λ , μ \lambda,\mu λ,μ为模型参数， C = F ⊤ F C=F^\top F C=F⊤F， F F F为变形梯度）。
  • 对比模型：MLP基线、数据增强MLP（4个随机旋转）、TFENN（等变方法）、本文方法。
  • 结果 ：本文方法在所有数据集规模（5k、20k、40k样本）下测试误差均显著低于其他模型，例如5k样本时，本文方法误差为 4.057 e − 6 ± 3.458 e − 7 4.057e-6 \pm 3.458e-7 4.057e−6±3.458e−7，远低于MLP基线（ 1.586 e − 4 ± 2.307 e − 6 1.586e-4 \pm 2.307e-6 1.586e−4±2.307e−6）和TFENN（ 5.3 e − 5 5.3e-5 5.3e−5）。

2. 路径签名估计（时间序列分析）

  • 问题 ：从路径的少量采样点估计路径签名（张量序列 S 0 , S 1 , . . . , S M S_0,S_1,...,S_M S0,S1,...,SM， S k S_k Sk为 k ( + ) k_{(+)} k(+)-张量），路径签名对重参数化不变，是路径数据的重要表征。
  • 对比模型：离散路径签名、同宽度MLP、同参数数量MLP、数据增强MLP、本文方法。
  • 结果 ：本文方法在正交群（ O ( d ) O(d) O(d)）和洛伦兹群下均表现最优。例如 O ( d ) O(d) O(d)场景中，本文方法误差为0.002，低于离散方法（1.336）和同参数MLP（0.071）；洛伦兹群场景中，本文方法误差0.029，优于同参数MLP（0.491）。

3. 稀疏向量估计（理论计算机科学）

  • 问题 ：从包含稀疏向量 v 0 v_0 v0的子空间的随机正交基 S S S中恢复 v 0 v_0 v0，涉及字典学习和张量PCA，对比SoS方法、MLP基线、本文方法（含Diag变体）。
  • 结果 ：
    • SoS方法在满足理论假设（如噪声向量单位协方差）时表现好，但在随机或对角协方差下性能下降。
    • 本文方法在SoS假设不满足时（如修正伯努利-高斯采样、随机协方差）表现更优，例如接受/拒绝采样+随机协方差场景，本文方法误差 0.938 ± 0.002 0.938 \pm 0.002 0.938±0.002，远高于SoS（ 0.610 ± 0.009 0.610 \pm 0.009 0.610±0.009）和MLP（ 0.241 ± 0.019 0.241 \pm 0.019 0.241±0.019）。
    • 所有实验中，MLP基线泛化能力差，验证了对称性对提升泛化的作用。

五、研究贡献与意义

  1. 理论贡献：提出首个张量等变机器学习的通用数学框架，明确给出正交群、洛伦兹群、辛群下，张量输入到张量输出的多项式和全纯等变函数的参数化方法，推广现有结果并融合张量不变量理论。
  2. 实践价值：基于理论开发的等变模型在材料科学（应力-应变）、时间序列（路径签名）、理论计算机科学（稀疏向量估计）三大领域均优于非等变基线，且能处理现有理论方法（如SoS）无法适配的场景。
  3. 可复现性：代码开源（匿名评审后发布），数据集可通过代码生成或公开获取，实验细节（模型结构、训练参数）在附录中详细说明，便于后续研究复用与扩展。

六、相关工作对比

相关工作 核心方法 局限性 本文方法优势
e3nn、escnn 基于不可约表示和Clebsch-Gordan系数 仅适配 S O ( d ) SO(d) SO(d)和 O ( d ) O(d) O(d)（ d = 2 , 3 d=2,3 d=2,3），需计算复杂系数 适配正交、洛伦兹、辛群，无需Clebsch-Gordan系数，参数化更通用
Kunisky et al. (2024) 对称张量 O ( d ) O(d) O(d)-不变多项式 不涉及学习应用，不支持不同阶/奇偶性张量、洛伦兹/辛群 面向机器学习场景，支持多类型张量和多群作用
Pearce-Crump (2023) O ( d ) / S O ( d ) / S p ( d ) O(d)/SO(d)/Sp(d) O(d)/SO(d)/Sp(d)等变神经网络 仅适用于特定输入输出张量幂次 输入输出张量类型更灵活，覆盖多场景
HotPP、GI-Net 外积和笛卡尔张量收缩 聚焦点云/图像的高阶张量构建 利用输入类型特性构建高效模型，适配多科学领域

论文中对称性在机器学习的核心应用与场景

论文围绕正交群（ O ( d ) O(d) O(d)）、洛伦兹群（ O ( s , d − s ) O(s,d-s) O(s,d−s)）、辛群（ S p ( d ) Sp(d) Sp(d)）等经典李群的对称性展开，将其融入机器学习模型设计，核心应用覆盖材料科学、时间序列分析、理论计算机科学三大领域，同时为对称性在机器学习中的通用适配提供了理论框架与实践方案。

七、核心应用场景：三大领域的对称性驱动优化

论文通过等变机器学习模型（利用群作用下的等变性约束），在三个典型问题中验证了对称性的实用价值，均实现对非等变基线模型的性能超越。

1. 材料科学：应力-应变张量关系学习

问题背景

超弹性材料（如neo-Hookean材料）的应力张量（ S S S）与应变张量（ C C C）满足 O ( d ) O(d) O(d)-等变性------张量在正交变换（如坐标旋转）下需保持变换一致性，且二者均为对称 2 ( + ) 2_{(+)} 2(+)-张量（向量外积生成，奇偶性为+1）。传统模型（如普通MLP）未考虑这种对称性，泛化能力差。

对称性应用逻辑
  • 理论依据 ：基于论文《推论2》， O ( d ) O(d) O(d)-等变函数对对称 2 ( + ) 2_{(+)} 2(+)-张量的输入输出，可转化为对张量特征值的置换等变函数------即先对输入应变张量 C C C做特征值分解（ C = Q Λ Q ⊤ C=Q\Lambda Q^\top C=QΛQ⊤），再通过置换等变网络处理特征值 Λ \Lambda Λ，最后重构应力张量 S = Q f ~ ( Λ ) Q ⊤ S=Q\tilde{f}(\Lambda)Q^\top S=Qf~(Λ)Q⊤。
  • 实验验证 ：对比普通MLP、数据增强MLP（随机旋转）、TFENN（现有等变方法）与本文模型，在5k、20k、40k样本规模下，本文模型测试误差均显著更低。例如5k样本时，本文模型误差为 4.057 e − 6 4.057e-6 4.057e−6，远低于普通MLP的 1.586 e − 4 1.586e-4 1.586e−4和TFENN的 5.3 e − 5 5.3e-5 5.3e−5。
核心价值

通过 O ( d ) O(d) O(d)对称性约束，模型无需依赖大量数据增强即可捕捉材料的各向同性特性，降低样本复杂度，提升对不同变形场景的泛化能力。

2. 时间序列分析：路径签名估计

问题背景

路径签名（Path Signature）是时间序列的关键张量表征，将连续路径 x : [ 0 , T ] → R d x:[0,T]\to\mathbb{R}^d x:[0,T]→Rd转化为张量序列 S 0 , S 1 , . . . , S M S_0,S_1,...,S_M S0,S1,...,SM（ S k S_k Sk为 k ( + ) k_{(+)} k(+)-张量），且对路径重参数化（如时间缩放）具有不变性。传统方法需从路径的大量采样点估计签名，而实际场景中常只有少量采样点，导致估计精度低。

对称性应用逻辑
  • 理论依据 ：路径签名的张量序列满足 O ( d ) O(d) O(d)（正交群）、洛伦兹群等对称性------例如正交变换下，路径的几何特征不变，对应签名张量需保持等变性。基于《推论1》和《推论3》，等变函数可表示为"输入向量外积+群对应张量（如 O ( d ) O(d) O(d)的克罗内克delta δ \delta δ、洛伦兹群的 I s , d − s \mathbb{I}_{s,d-s} Is,d−s）+索引置换"的线性组合，系数由输入向量的内积（或群特定双线性积）多项式参数化。
  • 实验验证 ：对比离散签名估计、同宽度MLP、同参数MLP，本文模型在 O ( d ) O(d) O(d)和洛伦兹群场景下均最优。例如 O ( d ) O(d) O(d)场景中，本文模型误差为0.002，低于离散方法的1.336和同参数MLP的0.071；洛伦兹群场景中，本文模型误差0.029，优于同参数MLP的0.491。
核心价值

通过对称性约束，模型从少量采样点即可精准估计路径签名，避免传统方法对密集采样的依赖，同时适配物理场景中的不同群作用（如欧氏空间的 O ( d ) O(d) O(d)、相对论场景的洛伦兹群）。

3. 理论计算机科学：稀疏向量估计

问题背景

从包含稀疏向量 v 0 v_0 v0的子空间中恢复 v 0 v_0 v0（如字典学习、张量PCA），传统方法（如Sum-of-Squares，SoS）依赖严格假设（如噪声向量协方差为单位矩阵、稀疏向量4-范数约束），当假设不满足时性能骤降；普通MLP因无结构约束，泛化能力差。

对称性应用逻辑
  • 理论依据 ：问题满足 O ( d ) O(d) O(d)-等变性------子空间的随机正交基 S S S在正交变换下（ S ↦ S M ( g ) S\mapsto SM(g) S↦SM(g)， g ∈ O ( d ) g\in O(d) g∈O(d)），稀疏向量 v 0 v_0 v0的恢复结果需保持不变。基于《推论1》，模型学习等变函数 h : ( R d ) n → R d × d h:(\mathbb{R}^d)^n\to\mathbb{R}^{d\times d} h:(Rd)n→Rd×d（输出对称矩阵），通过 v 0 = S ⋅ λ v e c ( h ( a 1 , . . . , a n ) ) v_0=S\cdot\lambda_{vec}(h(a_1,...,a_n)) v0=S⋅λvec(h(a1,...,an))（ λ v e c \lambda_{vec} λvec为最大特征向量）恢复稀疏向量，其中 h h h由"输入向量外积+内积多项式系数"构成。
  • 实验验证 ：在违反SoS假设的场景（如噪声协方差为随机矩阵、修正伯努利-高斯采样的稀疏向量），本文模型性能显著优于SoS和普通MLP。例如"接受/拒绝采样+随机协方差"场景，本文模型误差（ < v 0 , v ^ > 2 <v_0,\hat{v}>^2 <v0,v^>2）为0.938，远高于SoS的0.610和普通MLP的0.241。
核心价值

对称性约束使模型突破传统方法的假设限制，在非理想场景（如非单位协方差、低稀疏性）下仍能稳定恢复稀疏向量，提升模型的鲁棒性与适用范围。

八、通用理论应用：对称性驱动的等变模型框架

论文的核心贡献之一是提出张量等变机器学习的通用框架，将对称性应用从特定场景扩展到多群、多张量类型，为其他领域的对称性适配提供基础。

1. 多群适配：覆盖正交、洛伦兹、辛群

传统等变模型（如e3nn、escnn）仅适配 S O ( d ) SO(d) SO(d)或 O ( d ) O(d) O(d)（ d = 2 , 3 d=2,3 d=2,3），且依赖复杂的Clebsch-Gordan系数计算；本文框架通过"各向同性张量+群特定收缩"，统一适配三类经典李群：

  • 正交群（ O ( d ) O(d) O(d)） ：收缩操作使用克罗内克delta δ \delta δ，等变函数由输入张量外积与 δ \delta δ的组合构成；
  • 洛伦兹群（ O ( s , d − s ) O(s,d-s) O(s,d−s)） ：收缩操作使用闵可夫斯基内积对应的 I s , d − s \mathbb{I}_{s,d-s} Is,d−s，适配相对论场景的时空变换；
  • 辛群（ S p ( d ) Sp(d) Sp(d)） ：收缩操作使用辛积对应的 J d J_d Jd，适配经典/量子力学中的哈密顿系统。

2. 多张量类型适配：支持不同阶、奇偶性的张量

传统方法多限制输入输出为向量或低阶张量，本文框架通过《定理1》（ O ( d ) O(d) O(d)等变多项式）和《定理2》（洛伦兹/辛群等变全纯函数），支持任意阶（ k ( p ) k_{(p)} k(p)）、奇偶性（ p = ± 1 p=\pm1 p=±1）的张量输入输出，例如：

  • 输入为向量（ 1 ( + ) 1_{(+)} 1(+)-张量）、输出为2阶张量（ 2 ( + ) 2_{(+)} 2(+)-张量）（如应力-应变）；
  • 输入为多向量、输出为高阶张量（如路径签名）。

3. 模型设计范式：从理论到实践的落地路径

论文提供了明确的等变模型构建步骤，降低对称性应用的门槛：

  1. 确定群与张量类型 ：根据问题场景选择对应的群（如材料科学选 O ( d ) O(d) O(d)、相对论时间序列选洛伦兹群）和输入输出张量的阶与奇偶性；
  2. 基于推论参数化函数 ：若输入为向量，使用《推论1》（ O ( d ) O(d) O(d)）或《推论3》（洛伦兹/辛群），将函数表示为"向量外积+群张量+置换"的组合，系数由内积多项式（或全纯函数）参数化；
  3. 结合神经网络实现：将系数的多项式/全纯函数用MLP近似（如路径签名估计中，系数由输入向量内积的共享MLP学习），确保模型端到端可训练。

九、对称性在机器学习中的通用价值

除上述具体场景外，论文还揭示了对称性在机器学习中的底层作用，为其他领域提供参考：

  1. 降低样本复杂度：对称性约束本质是注入领域先验（如材料各向同性、路径几何不变性），减少模型对数据的依赖，例如材料科学中无需大量旋转数据增强；
  2. 提升泛化能力：非等变模型易过拟合特定数据分布，而对称性确保模型捕捉"与变换无关的核心特征"，例如稀疏向量估计中对不同噪声协方差的鲁棒性；
  3. 增强物理一致性：在科学机器学习（AI for Science）中，对称性是物理定律的核心（如相对论的洛伦兹不变性、量子力学的辛对称性），等变模型可确保预测结果符合物理规律，避免非物理输出；
  4. 简化模型设计：传统等变模型需针对特定群设计复杂的表示分解（如不可约表示），本文框架通过"各向同性张量+收缩"统一参数化，无需依赖Clebsch-Gordan系数等复杂计算，降低实现难度。

十、与现有对称性应用的对比优势

论文通过对比现有工作，凸显了其对称性应用的创新性（如表1所示）：

相关工作 适配群范围 张量类型支持 核心局限 本文方法优势
e3nn、escnn S O ( d ) SO(d) SO(d)、 O ( d ) O(d) O(d)（ d = 2 , 3 d=2,3 d=2,3） 有限阶张量 依赖Clebsch-Gordan系数，群适配少 覆盖正交、洛伦兹、辛群，无需复杂系数
Kunisky et al. O ( d ) O(d) O(d) 对称张量 无学习应用，不支持多群 面向机器学习场景，多群多张量适配
Pearce-Crump O ( d ) O(d) O(d)、 S O ( d ) SO(d) SO(d)、 S p ( d ) Sp(d) Sp(d) 特定幂次张量 输入输出张量类型受限 支持任意阶/奇偶性张量

综上，论文中对称性的应用不仅解决了三大领域的具体问题，更提供了一套"多群-多张量-可学习"的通用等变框架，为对称性在机器学习中的广泛落地（如量子力学模拟、相对论时空数据处理）奠定基础。

相关推荐
yumgpkpm6 小时前
（简略）AI 大模型 手机的“简单替换陷阱”与Hadoop、Cloudera CDP 7大数据底座的关系探析
人工智能·hive·zookeeper·flink·spark·kafka·开源
会编程的吕洞宾6 小时前
智能体学习记录一
人工智能·学习
TG：@yunlaoda360 云老大6 小时前
腾讯云国际站代理商的NLP服务可以提供哪些定制化功能？
自然语言处理·云计算·腾讯云
Robert--cao6 小时前
人机交互（如 VR 手柄追踪、光标移动、手势识别）的滤波算法
人工智能·算法·人机交互·vr·滤波器
Z3r4y6 小时前
【AI】2025 0x401新生交流赛 wp
人工智能·ai·ctf·wp
智驱力人工智能6 小时前
高速公路无人机车流密度监测 构建动态交通新维度 基于YOLOv8的无人机车辆检测算法 边缘计算无人机交通监测设备
人工智能·安全·yolo·目标检测·视觉检测·无人机·边缘计算
Katecat996636 小时前
基于YOLOv8-Slimneck-WFU模型的苹果目标检测实现
人工智能·yolo·目标检测
Piar1231sdafa6 小时前
FCOS模型优化实战：基于R50-DCN-Caffe的FPN_GN检测头中心点回归与GIoU损失函数实现
人工智能·回归·caffe
世岩清上6 小时前
智能算法与边缘计算融合：驱动下一代实时决策系统的技术范式革新
人工智能·边缘计算
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser08BongoCat - 跨平台键盘猫动画工具09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）