概述
逻辑回归是一种用于解决二分类问题 的统计方法,尽管名称中包含"回归",但实际上是一种分类算法。 它通过将线性回归的输出映射到Sigmoid函数,将预测值转换为概率值(0到1之间),从而进行分类决策。
逻辑回归的核心目标是:
预测一个样本属于某个类别的概率。
数学原理和推导
1. 假设函数(sigmoid 函数)
逻辑回归通过将线性回归的结果输入一个S型函数,将结果映射到 0 到 1 的区间:
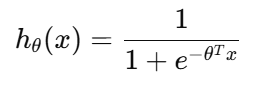
其中:
hθ(x)是预测结果(属于类别1的概率)
θ是参数向量(权重)
x 是输入特征向量
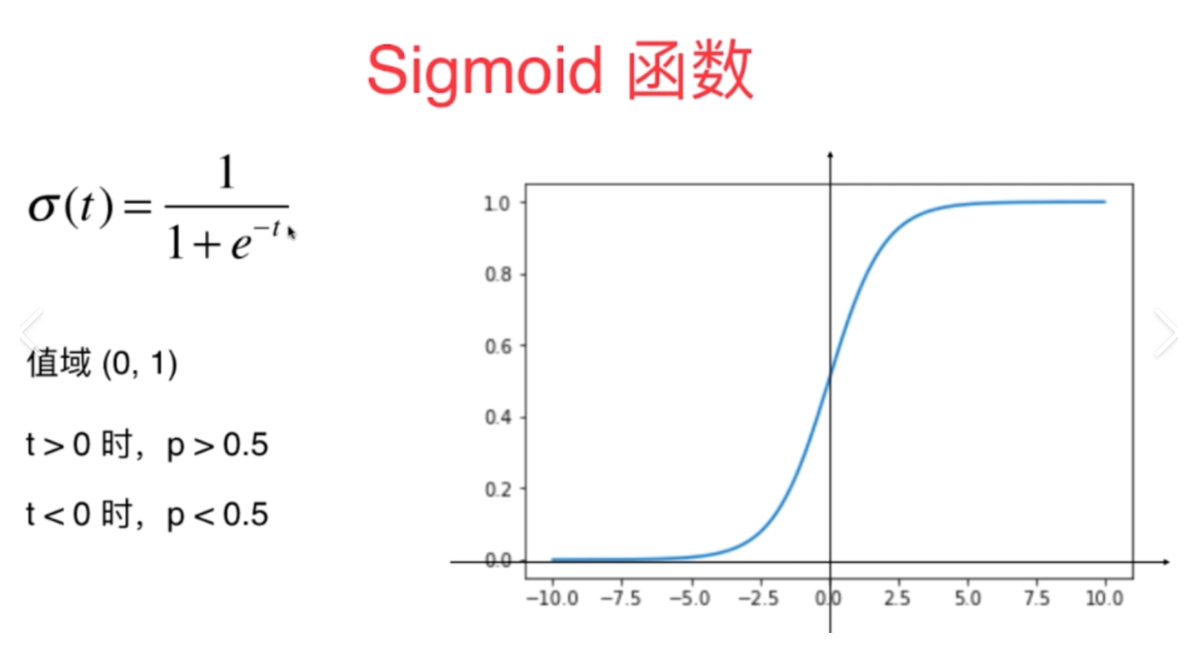
当t趋近于正无穷,函数值越趋近于1,反之,越趋近于负无穷,函数值越趋近于0
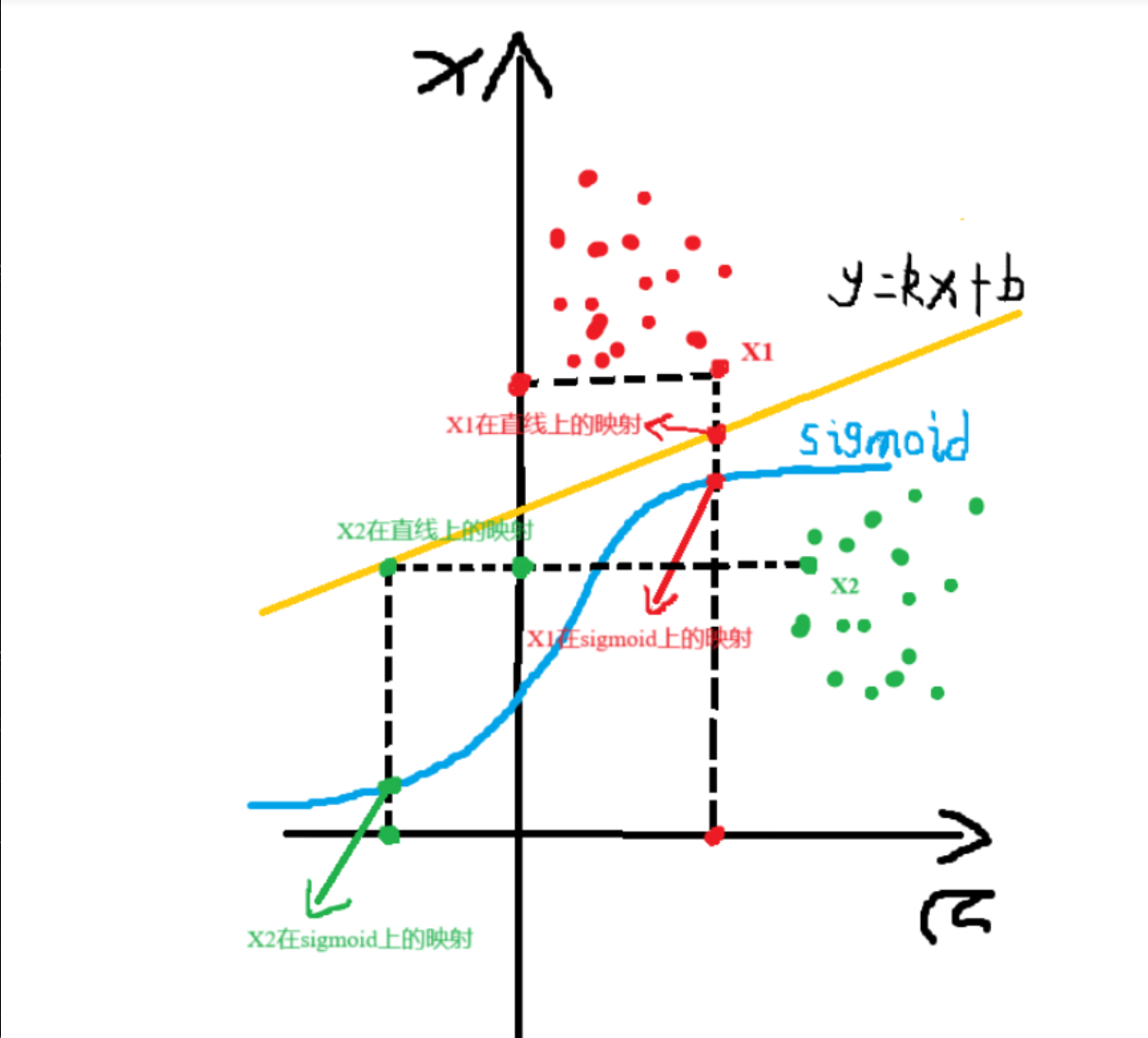
2.决策边界
当: hθ(x)≥0.5,预测为类别1
hθ(x)<0.5,预测为类别0
3. 损失函数(对数损失)
逻辑回归使用最大似然估计来求解
其对应的损失函数为:
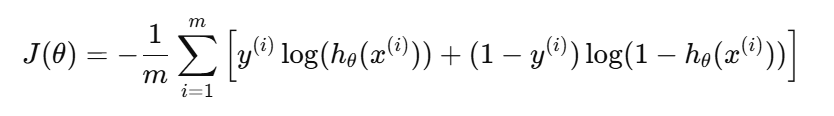
其中:m表示样本数量
y^(i) 表示第i个样本的标签
这个损失函数的目标是最小化预测与真实标签之间的差异
逻辑回归的训练方式
最大似然估计
逻辑回归通过最大似然估计(MLE)来求解模型参数。其核心思想是找到一组参数,使得观测到的数据在该参数下的概率(似然)最大化。
梯度下降法(本质是寻找合适的参数)
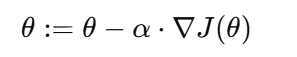
其中:α是学习率
∇J(θ)是损失函数的梯度
梯度的概念:
1.在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
2.在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
梯度下降的核心:
1.方向
2.步长(学习率)
3.沿着方向和步长持续更新参数
梯度下降的方式:
1.批量梯度下降(BGD)
容易得到最优解,但是每次考虑所有样本,运算速度比较慢
2.随机梯度下降(SGD)
优点:由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快
缺点:可能回收敛到局部最优,因为单个样本并不能代表全体样本的趋势
总结:每次寻找一个样本,迭代速度快,但不一定每次都朝着收敛的方向
3.小批量梯度下降(MBGD)
每次更细选择一小部分数据来算
牛顿法
牛顿法(Newton's Method)是一种迭代优化算法,用于求解函数的零点或极值点。在逻辑回归中,牛顿法用于最大化对数似然函数,从而找到最优的模型参数。
优点:
收敛速度快(二阶收敛)。
适用于参数维度不高的问题。
缺点:
计算 Hessian 矩阵及其逆矩阵的复杂度高,不适合高维数据。
需要保证 Hessian 矩阵正定,否则可能不收敛。
正则化惩罚
为了防止过拟合,可以在损失函数中加入正则化项:
L1正则(Lasso):鼓励稀疏解
L2正则(Ridge):平滑模型参数
python
# 带正则化项的逻辑回归
model = LogisticRegression(penalty='l2', C=1.0) # C 越小,正则化越强参数介绍:Penalty:正则化方式,有l1和l2两种。用于指定惩罚项中使用的规范。
C:正则化强度。为浮点型数据。正则化系数λ的倒数,float类型,默认为1.0。必须是正浮点型数。像SVM一样,越小的数值表示越强的正则化。
max_iter:算法收敛最大迭代次数,int类型,默认为100。仅在正则化优化算法为newtoncg, sag和lbfgs才有用,算法收敛的最大迭代次数。
逻辑回归的评价方式
混淆矩阵:
- 真阴性(TN):非 0 数字被正确预测的数量;
- 真阳性(TP):0 被正确预测的数量;
- 假阴性(FN):0 被误判为非 0 的数量;
- 假阳性(FP):非 0 被误判为 0 的数量




准确率:适用于类别平衡的数据集,但对不平衡数据可能产生误导。
精确率:适用于需要高置信度正类预测的场景(如垃圾邮件分类)
召回率:适用于漏报成本高的场景(如疾病检测)
F1分数:适用于需要平衡精确率和召回率的场景。
逻辑回归的优缺点
优点
- 可解释性强:参数 θj 表示特征 j 对 "正类概率" 的影响程度,结合系数正负可分析特征的作用方向;
- 训练高效:计算复杂度低,适合处理大规模数据;
- 鲁棒性较好:对噪声不敏感,无需复杂的特征工程也能得到不错的效果;
- 输出概率值:不仅能分类,还能给出分类的置信度,便于后续决策。
缺点
- 线性假设:仅能捕捉线性关系,对非线性数据拟合效果差(可通过特征交叉、多项式特征改进);
- 对异常值敏感:极端值会影响参数估计,需提前做数据清洗;
- 仅适用于二分类:处理多分类需扩展(如 One-Vs-Rest、Softmax 回归)
逻辑回归与线性回归的区别
目标函数不同
线性回归用于预测连续数值,通过最小化平方误差损失函数拟合数据。逻辑回归用于分类问题,通过最大化似然函数(或最小化对数损失)预测概率,输出范围为[0,1]。
输出类型不同
线性回归输出无限制的实数值,逻辑回归输出概率值,通过Sigmoid函数映射:
假设条件不同
线性回归假设误差项服从正态分布,且特征与目标呈线性关系。逻辑回归假设数据满足sigmoid 函数
评估指标不同
线性回归常用均方误差(MSE)、R²等指标。
逻辑回归使用准确率、精确率、召回率、AUC-ROC等分类指标。
应用场景不同
线性回归适用于房价预测、销量分析等连续值预测。
逻辑回归适用于银行贷款违约预测、垃圾邮件分类、疾病诊断等二分类或多分类任务。