hot100 128.最长连续序列

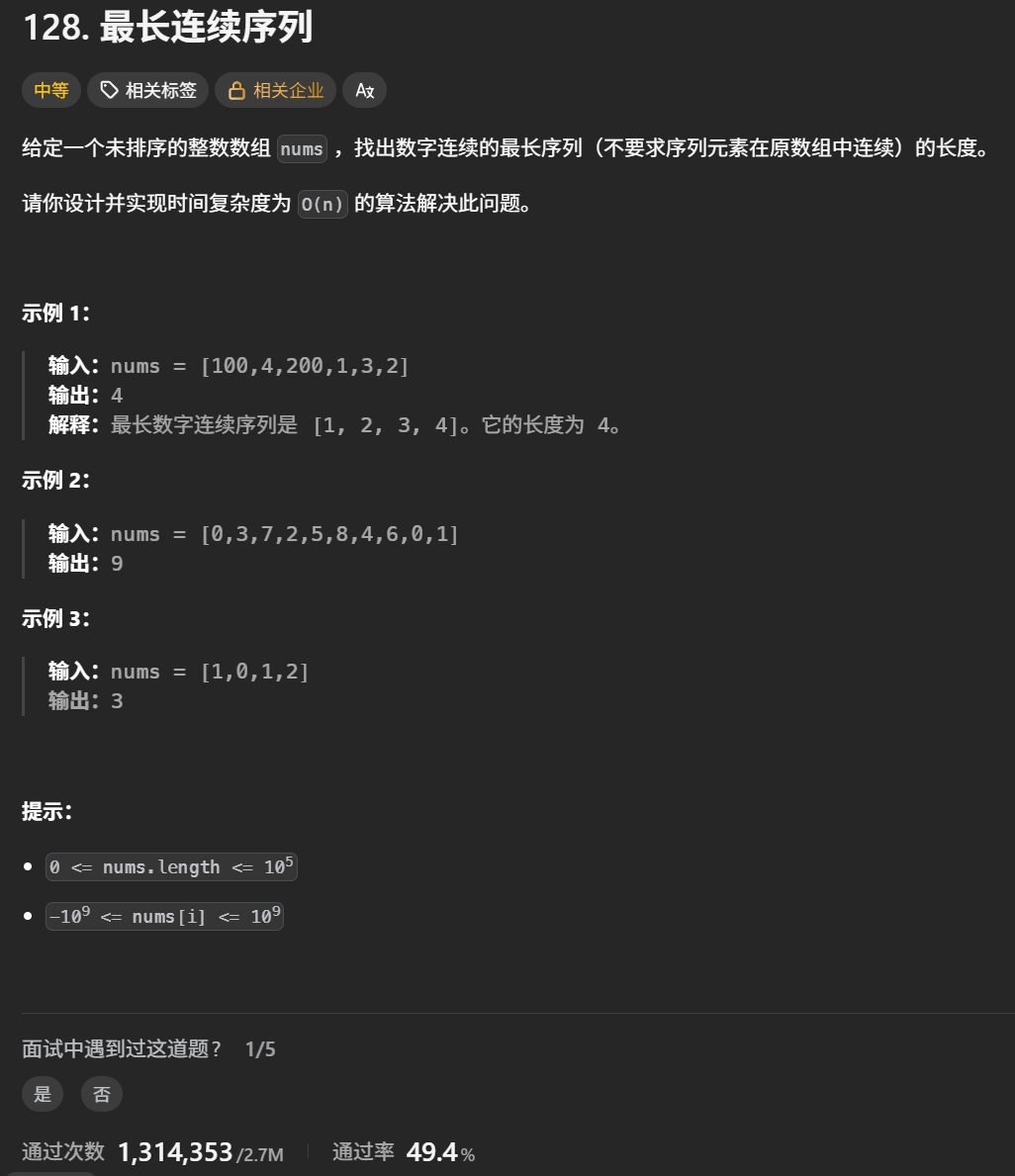
思路：

1.题目要求时间复杂度为O(n)，而排序的时间复杂度是O(nlogn)，因此本题不能排序。

2.核心思路：对于nums中的元素x，以x为起点，不断查找下一个数x + 1，x + 2，...是否在nums中，并统计序列的长度。

3.为了做到O(n)的时间复杂度，需要做到两个关键优化。

（1）把nums中的数都放到一个哈希集合中，这样可以以O(1)的时间复杂度判断数字是否在nums中。

（2）如果x - 1在哈希集合中，则不以x为起点。这是因为以x - 1为起点计算出的序列长度，一定要比以x为起点计算出的序列长度要长，这样可以避免大量重复计算。比如nums == $3,2,4,5$ ，从3开始，可以找到3，4，5这个连续序列；而从2开始，则可以找到2，3，4，5这个连续序列，一定比从3开始找到的连续序列要长。

4.注意：遍历元素的时候，要遍历哈希集合，而不是nums。如果nums = $1,1,1,...,1,2,3,4,5,...$ （前一半都是1），遍历nums的做法会导致每个1都跑一个O(n)的循环，总的循环次数是O(n^2)，会超时。

附代码：

java 复制代码

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums){
            set.add(num); //把nums转换成哈希集合
        }
        int ans = 0;
        for(int x : set){ //遍历哈希集合
            if(set.contains(x - 1)){
                //如果x不是序列的起点，则直接跳过
                continue;
            }
            //x是序列的起点
            int y = x + 1;
            while(set.contains(y)){ //不断查找下一个数是否在哈希集合中
                y++;
            }
            // 循环结束后，y - 1就是最后一个在哈希集合中的数
            // 长度为 y - 1 - x + 1 = y - x
            ans = Math.max(ans,y - x);
        }
        return ans;
    }
}

小优化：设m为nums中不同元素的个数（即哈希集合的大小）。各个连续序列（链）是相互独立的，如果发现其中一条链的长度至少为m/2（长度×2＞＝m），由于不可能还有一条长度大于m/2的链（否则这两条链的长度之和就超过m了），答案不会再增大，此时可以直接返回答案。

java 复制代码

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums){
            set.add(num); //把nums转换成哈希集合
        }
        int m = set.size();
        int ans = 0;
        for(int x : set){ //遍历哈希集合
            if(set.contains(x - 1)){
                //如果x不是序列的起点，则直接跳过
                continue;
            }
            //x是序列的起点
            int y = x + 1;
            while(set.contains(y)){ //不断查找下一个数是否在哈希集合中
                y++;
            }
            // 循环结束后，y - 1就是最后一个在哈希集合中的数
            // 长度为 y - 1 - x + 1 = y - x
            ans = Math.max(ans,y - x);
            if(ans * 2 >= m){
                break;
            }
        }
        return ans;
    }
}