Graphiti：Cypher与SQL的“同声传译“，一个让图数据库和关系数据库握手言和的验证器

Debroon2025-12-17 10:46

Graphiti：Cypher与SQL的"同声传译"，一个让图数据库和关系数据库握手言和的验证器

论文：https://arxiv.org/abs/2504.03182

发明Graphiti：从"鸡同鸭讲"到"同声传译"

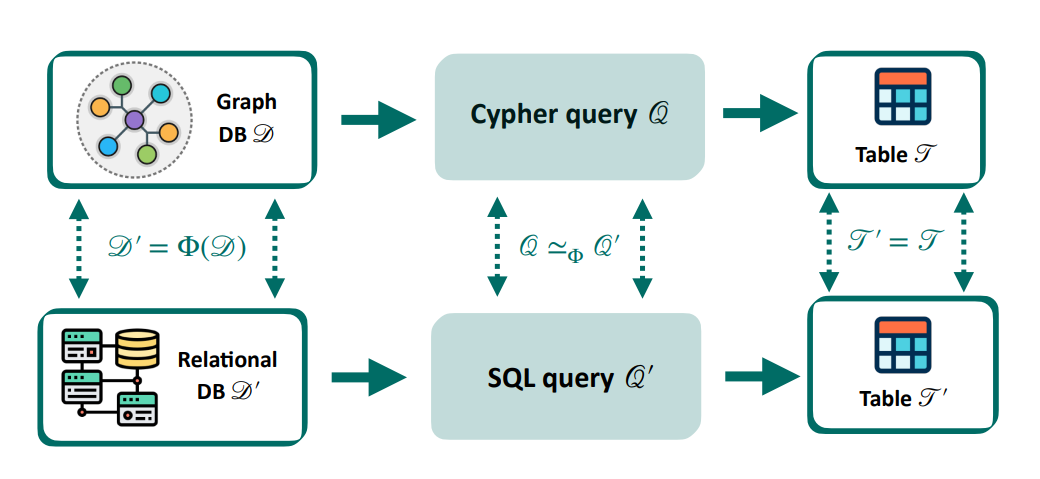
如果你有一个图数据库的查询，想知道它和一个SQL查询是不是做同一件事------

直接比较？不可能。一个操作节点和边，一个操作表和行，根本不是同一种东西。

就像拿中文问英文"我们说的是不是一个意思"，没有翻译，永远说不清。

于是，你决定先翻译。

把图查询翻译成SQL，再比较两个SQL------这就变成同一种语言了。

可问题又来了：图里的"路径"在SQL里叫什么？

你盯着图查询看：从A节点，沿着R边，走到B节点。

再看SQL：从A表，通过外键JOIN到关系表，再JOIN到B表。

本质上，都是"找有关联的数据"。

于是你写下第一条翻译规则：路径 = JOIN。

可问题又来了：图数据库的结构千奇百怪，每次都得重新想怎么翻译？

你需要一个标准格式。

于是，你定义"诱导关系模式"：

  • 每种节点类型 → 一张表
  • 每种边类型 → 一张表（带两个外键，指向源和目标）

不管用户的图长什么样，先统一翻译成这个标准格式。

这样，翻译规则就固定了，可以自动生成。

可问题又来了：用户实际的SQL用的是另一套表结构，和你的标准格式对不上。

你需要一个"转接头"。

于是，你引入"残差转换器"：描述标准格式到用户格式的映射。

用户只需要告诉你：图里的CONCEPT对应他的Concept表，边对应哪张表。

剩下的，你自动推导。

可问题又来了：翻译完了，怎么验证两个SQL是不是等价？

你不想重新造轮子。

于是，你直接调用现成的SQL验证工具：

  • VeriEQL：能找反例，证明"不等价"
  • Mediator：能做完整证明，确认"等价"

两个工具互补，一个找bug，一个做保证。

可问题又来了：这套方法真的管用吗？

你用410个真实案例测试。

结果：

  • 发现34个bug，包括Neo4j官方教程里的错误
  • 77.6%的查询可以完全证明等价
  • GPT翻译的查询有13%是错的------你的工具全都揪出来了

翻译速度？平均6.3毫秒。

恭喜你，发明了Graphiti。

它能把Cypher查询翻译成SQL，再自动验证两者是否等价。

这不仅是一个翻译器，更是数据库迁移时的"语义保险"------确保你的新系统和老系统说的是同一件事。

核心演化路径总结

问题 解法 关键数据
图和表无法直接比较 把图查询翻译成SQL 路径=JOIN
翻译规则不统一 定义诱导关系模式+SDT 自动生成
用户schema不同 残差转换器RDT 语法替换
需要验证等价性 复用VeriEQL/Mediator 34个bug被发现
方法是否有效 410个benchmark测试 77.6%完全验证，翻译6.3ms

本质升华： 把"跨模型验证"降维成"同模型验证"------不是教两种语言互相理解，而是都翻译成同一种语言再比较。

用毛选分析方法解读《Graphiti》论文

一、矛盾分析法

1. 正面与负面的统一

正面（机会）：

  • 图数据库灵活，适合表达复杂关系
  • 关系数据库成熟，有完善的验证工具
  • 两种数据库各有应用场景，企业有迁移需求

负面（风险）：

  • 人工翻译普遍出错（论文发现34个bug，包括官方教程）
  • GPT翻译有13%的错误率
  • 两种数据模型根本不同，直接比较困难

作者的"一分为二"：

作者没有说"图数据库好"或"关系数据库好"，而是看到：

两种模型各有优势，问题在于如何正确地在它们之间转换

这就是从矛盾的正反两面把握问题。别人看到的是"翻译难"，作者看到的是"翻译错误暴露了验证工具的缺失"------风险与机会相伴。

2. 共性与个性的统一

共性（普遍规律）：

  • 图数据库的"边"和关系数据库的"join"，本质上都是在描述实体之间的关联
  • 两种查询语言最终都返回一张表
  • 数据库验证的核心问题都是"语义等价性"

个性（特殊情况）：

  • Cypher的路径模式是显式的图遍历
  • SQL的join是隐式的表连接
  • 每个用户的目标schema可能与标准schema不同

作者如何处理共性与个性的关系：

论文的核心洞察正是抓住了共性：

"paths in a graph database instance correspond to joins of rows in a relational database"

但作者没有变成"教条主义者"------他引入了database transformer来处理个性：

  • 标准转换器（SDT）处理共性情况
  • 残差转换器（RDT）处理用户特定schema的个性情况

这就是从个性到共性，再到个性的认识过程：

  1. 观察具体的Cypher-SQL翻译案例（个性）
  2. 发现"路径≈join"的普遍规律（共性）
  3. 应用到任意用户schema的具体验证中（回到个性）

3. 对立与同一的统一

矛盾的对立面：

图数据库 关系数据库
节点和边 表和行
模式匹配 Join操作
灵活schema 严格schema
验证工具缺乏 验证工具成熟

矛盾的转化------作者的高明之处：

面对"如何验证图查询与关系查询的等价性"这个难题，作者没有正面硬刚，而是从对立面入手：

"instead of directly reasoning about equivalence between Cypher and SQL queries---which would require complex SMT encodings that combine graph and relational structures---we reduce the problem to checking equivalence between SQL queries"

翻译：不直接验证图-关系等价，而是把图查询翻译成SQL，变成SQL-SQL等价验证。

这正是教员说的：

"为了前进而后退，为了正面而侧面，为了走直路而走弯路。"

正面是图-关系验证，但太难；侧面是SQL-SQL验证，工具成熟。通过引入中间表示，把对立的两个世界统一到一个世界中。

二、透过现象看本质

现象层面（表象）

现象1： 开发者在论坛上频繁询问"这个SQL怎么翻译成Cypher"
现象2： 学术论文中的翻译例子被发现是错的
现象3： Neo4j官方教程的例子也有语义不等价的问题
现象4： GPT翻译的Cypher有13%的错误率

如果只看现象，可能得出结论：

  • "翻译很难，需要更多练习"
  • "GPT还不够智能"
  • "需要更好的教程"

本质层面（根源）

作者透过现象抓住了本质：

问题的根源不是翻译能力不足，而是缺乏验证手段。

为什么这是本质？因为：

  • 无论翻译者水平多高，都可能犯错
  • 没有验证工具，就无法发现错误
  • 这是一个系统性缺陷，而非个体能力问题

进一步追问本质：为什么没有验证工具？

因为图数据库和关系数据库的数据模型根本不同，无法直接比较。

这才是主要矛盾：两种数据模型的异构性。

抓住本质后的解决思路

既然本质是"数据模型不同导致无法比较"，那么解决方案就是：

  1. 定义等价关系（database transformer）
  2. 统一数据模型（把Cypher翻译成SQL）
  3. 复用成熟工具（VeriEQL、Mediator）

这就是教员说的：

"一进了门就要抓住它的实质，这才是可靠的科学的分析方法。"

三、时间与空间的方法

时间维度：过去、现在、将来

过去（历史背景）：

  • SQL等价性验证已有大量研究 [10-12, 55]
  • Schema mapping理论已经成熟 [17, 35, 57]
  • 数据迁移工具已经存在（如Dynamite）

现在（现状问题）：

  • 图-关系等价验证是空白
  • 现有工具只能验证SQL-SQL，不能验证Cypher-SQL

将来（发展方向）：

论文结尾提到：

"we plan to explore the development of a graphical interface for specifying database transformers"

作者的历史视角让他意识到：不需要从零开始造轮子。

  • Schema mapping的历史 → 借鉴transformer语言
  • SQL验证的历史 → 复用VeriEQL和Mediator
  • 数据迁移的历史 → 参考Dynamite的思路

这正是教员的方法：

"要研究一个事物，必须要从它的全部历史状况出发"

空间维度：局部与全局

局部视角（只看问题本身）：

  • Cypher有什么语法？
  • SQL有什么语法？
  • 怎么一一对应翻译？

全局视角（把视线抬高）：

作者没有局限于"怎么翻译"，而是看到了更大的图景：

复制代码 
              ┌─────────────────────────────────────┐
              │         程序验证的整体生态           │
              │  ┌───────┐  ┌───────┐  ┌───────┐   │
              │  │SQL验证│  │图数据库│  │迁移工具│   │
              │  └───────┘  └───────┘  └───────┘   │
              └─────────────────────────────────────┘
                          ↓ 全局思考
              "能不能把图查询验证归约到SQL验证？"

这就像教员在东北战役中的视角：

  • 林只看到长春（局部）
  • 教员看到锦州（全局战略要点）

作者也是：

  • 直接验证图-关系等价（攻长春，硬碰硬）
  • 归约到SQL等价验证（打锦州，切断关键通道）

全局视角的体现：

论文图1清晰展示了全局架构：

复制代码 
Schemas → SDT inference → SDT
    ↓                      ↓
   Q_G → Transpiler → Q'_R → SQL checker → ✓/✗
    ↓                      ↑
   Q_R ──────────────────→ RDT inference

这不是"怎么翻译一条查询"的局部思考，而是"怎么设计一套完整的验证系统"的全局思考。

四、综合分析：作者解决问题的方法论

第一步：找准主要矛盾

主要矛盾：图数据库和关系数据库数据模型的异构性

次要矛盾：

  • 翻译规则的复杂性
  • 验证工具的选择
  • 用户schema的多样性

作者没有被次要矛盾牵着走，而是集中精力解决主要矛盾。

第二步：矛盾转化

把"图-关系验证"这个难题，转化为"SQL-SQL验证"这个已解决的问题。

这是典型的矛盾转化策略：正面攻不下，从对立面入手。

第三步：共性与个性结合

  • 用SDT处理共性（标准翻译）
  • 用RDT处理个性（用户特定schema）
  • 既不教条（只用SDT），也不经验主义（每次都手写转换规则）

第四步：实践验证

410个benchmark的实验验证，包括：

  • 真实世界的bug发现（3个来自野外）
  • 人工翻译的bug发现（4个）
  • GPT翻译的bug发现（27个）

这正是《实践论》的方法：认识来源于实践，又要回到实践中检验。

五、结论

用毛选方法分析这篇论文，可以看到作者的思维方式暗合辩证法：

毛选方法 论文体现
一分为二 看到图数据库和关系数据库各自的优缺点
共性与个性 SDT处理共性，RDT处理个性
对立同一 把图-关系验证转化为SQL-SQL验证
透过现象看本质 从"翻译错误"现象看到"验证缺失"本质
时间维度 借鉴schema mapping、SQL验证的历史成果
空间维度 从全局视角设计系统，而非局部解决翻译问题

最精妙的一笔：引入中间层（induced schema + SDT）

这就像教员说的"走弯路反而办成事"------不直接比较图和表，而是先把图翻译成标准的表，再比较两个表。表面上多走了一步，实际上化繁为简，一通百通。

Graphiti论文解法深度拆解

一、解法的整体结构

问题定义

输入： 图数据库查询（Cypher） Q G Q_G QG、关系数据库查询（SQL） Q R Q_R QR、两种数据库的schema、数据库转换器 Φ \Phi Φ

输出： 判断 Q G ≅ Φ Q R Q_G \cong_\Phi Q_R QG≅ΦQR（两个查询在转换器 Φ \Phi Φ下是否语义等价）

核心公式形式

Q G ≅ Φ Q R    ⟺    Transpile ( Q G ) ≅ Φ r d t Q R Q_G \cong_\Phi Q_R \iff \text{Transpile}(Q_G) \cong_{\Phi_{rdt}} Q_R QG≅ΦQR⟺Transpile(QG)≅ΦrdtQR

即：图-关系等价验证 = 翻译 + SQL-SQL等价验证

与同类算法的主要区别

对比维度 直接验证方法（不存在） Graphiti方法
验证对象 图查询 vs SQL查询 SQL查询 vs SQL查询
编码复杂度 需要同时编码图和表 只需编码表
工具复用 需要从零构建 复用现有SQL验证器
核心洞察 无 路径模式 ≈ Join操作

二、解法拆解：特征-子解法对应

总体解法结构

解法 = SDT推断 ⏟ 特征A + 语法导向翻译 ⏟ 特征B + 残差转换器推断 ⏟ 特征C + SQL等价验证 ⏟ 特征D \text{解法} = \underbrace{\text{SDT推断}}{\text{特征A}} + \underbrace{\text{语法导向翻译}}{\text{特征B}} + \underbrace{\text{残差转换器推断}}{\text{特征C}} + \underbrace{\text{SQL等价验证}}{\text{特征D}} 解法=特征A SDT推断+特征B 语法导向翻译+特征C 残差转换器推断+特征D SQL等价验证

特征A：图数据库和关系数据库的数据模型根本不同

↓ 为什么需要专门解法：

  • 如果不处理：无法定义"等价"的含义
  • 节点/边 vs 表/行，没有直接对应关系
  • 无法在同一语义空间内比较两个查询

↓ 子解法设计：

方案 具体做法 优点 缺点
方案1：用户手写映射 用户为每对(图schema, 关系schema)写映射规则 灵活 工作量大，易出错
方案2：定义标准转换 自动从图schema推导出"诱导关系schema"和SDT 自动化，一致性强 可能与用户期望的schema不同
最终选择 方案2 + 残差转换器补偿 兼顾自动化和灵活性 需要额外的RDT推断步骤

↓ 实施要点：

关键动作：

  1. 节点类型 → 表（属性 → 列，默认属性 → 主键）
  2. 边类型 → 表 + 两个外键（指向源/目标节点表的主键）
  3. 生成SDT公式： l ( K 1 , . . . , K n ) → R l ( K 1 , . . . , K n ) l(K_1,...,K_n) \rightarrow R_l(K_1,...,K_n) l(K1,...,Kn)→Rl(K1,...,Kn)

成功标准：

  • 对任意图实例 G G G， Φ s d t ( G ) \Phi_{sdt}(G) Φsdt(G)产生唯一确定的关系实例 R ′ R' R′
  • 转换保持信息完整性（可逆）

风险预案：

  • 如果用户schema与诱导schema差异太大 → 用RDT补偿
  • 如果图schema有歧义 → 要求用户明确默认属性键

之所以用"诱导schema + SDT"子解法，是因为"数据模型异构"特征。

例子： 图schema有节点EMP(id, name)和边WORK_AT(wid) → 诱导出表emp(id, name)和表work_at(wid, SRC, TGT)，其中SRC、TGT是外键。

特征B：Cypher的路径模式没有SQL直接对应物

↓ 为什么需要专门解法：

  • 如果不处理：MATCH (a)-[:R]->(b) 在SQL中无法表达
  • Cypher的模式匹配是显式遍历图结构
  • SQL只有表之间的Join操作

↓ 子解法设计：

方案 具体做法 优点 缺点
方案1：语义编码 把Cypher语义直接编码为SMT公式 理论上完整 需要新的验证器，复杂度高
方案2：语法导向翻译 利用"路径≈Join"洞察，逐语法结构翻译 可复用SQL工具 需要证明翻译正确性
最终选择 方案2：语法导向翻译 简单、可证明、可复用 只支持Featherweight Cypher子集

↓ 实施要点：

关键动作：

  1. 节点模式 ( X , l ) (X, l) (X,l) → ρ X ( R l ) \rho_X(R_l) ρX(Rl)（表重命名）
  2. 路径模式 → Join链（通过外键连接）
  3. Match子句 → Inner Join
  4. OptMatch子句 → Left Outer Join
  5. Return + 聚合 → GroupBy

成功标准：

  • 定理5.7：翻译结果语义等价于原Cypher查询（模SDT）
  • 定理5.8：所有Featherweight Cypher查询都能被翻译

风险预案：

  • 遇到不支持的Cypher特性（如变长路径） → 报错，建议用户简化查询

之所以用"语法导向翻译"子解法，是因为"路径模式无直接SQL对应"特征。

例子：

复制代码 
Cypher: MATCH (n:EMP)-[:WORK_AT]->(m:DEPT)
SQL:    emp AS n JOIN work_at AS e ON n.id=e.SRC 
                 JOIN dept AS m ON e.TGT=m.dnum

特征C：用户的目标schema可能与诱导schema不同

↓ 为什么需要专门解法：

  • 如果不处理：翻译出的SQL在诱导schema上，用户SQL在不同schema上，无法直接比较
  • 实际项目中，关系数据库schema是已存在的，不可能改成诱导schema
  • 例如：用户schema把边的属性合并到了节点表中

↓ 子解法设计：

方案 具体做法 优点 缺点
方案1：强制用户用诱导schema 不支持其他schema 实现简单 实用性差
方案2：每次手写schema映射 用户提供完整的转换规则 灵活 工作量大
方案3：计算残差转换器 从用户转换器 Φ \Phi Φ和SDT自动推导RDT 自动化 需要 Φ \Phi Φ和SDT形式兼容
最终选择 方案3：残差转换器 用户只需提供 Φ \Phi Φ，其余自动计算 依赖语法替换的简单性

↓ 实施要点：

关键动作：

  1. 从SDT提取映射： σ = { P 1 ↦ P 0 ∣ P 1 ( . . . ) → P 0 ( . . . ) ∈ Φ s d t } \sigma = \{P_1 \mapsto P_0 \mid P_1(...) \rightarrow P_0(...) \in \Phi_{sdt}\} σ={P1↦P0∣P1(...)→P0(...)∈Φsdt}
  2. 对用户转换器 Φ \Phi Φ应用替换： Φ r d t = Φ [ σ ] \Phi_{rdt} = \Phi[\sigma] Φrdt=Φ[σ]
  3. 将RDT传递给SQL验证器

成功标准：

  • Φ r d t \Phi_{rdt} Φrdt正确描述诱导schema到用户schema的转换
  • 定理5.9-5.10：归约保持等价性

风险预案：

  • 如果 Φ \Phi Φ过于复杂，RDT可能导致验证超时 → 建议用户简化schema映射

之所以用"残差转换器"子解法，是因为"用户schema与诱导schema不同"特征。

例子：

  • SDT: CONCEPT(cid,name) → Concept'(cid,name)
  • 用户 Φ \Phi Φ: CONCEPT(cid,name) → Concept(cid,name)
  • RDT: Concept'(cid,name) → Concept(cid,name)

特征D：需要实际验证两个SQL查询的等价性

↓ 为什么需要专门解法：

  • 如果不处理：即使翻译正确，也无法确认最终等价性
  • SQL等价性验证本身是不可判定问题
  • 需要在soundness和completeness之间权衡

↓ 子解法设计：

方案 具体做法 优点 缺点
方案1：有界模型检查 在有限大小的数据库上穷举（VeriEQL） 能找反例 不能证明等价
方案2：演绎验证 用SMT求解器证明等价（Mediator） 能证明等价 不支持聚合，可能超时
最终选择 可插拔后端，两者皆可用 灵活选择 需要维护两套接口

↓ 实施要点：

关键动作（VeriEQL后端）：

  1. 设置10分钟超时
  2. 逐步增加符号表大小（从小到大）
  3. 找到反例即停止，否则报告有界验证通过

关键动作（Mediator后端）：

  1. 检查查询是否在支持片段内（无聚合、无外连接）
  2. 生成验证条件
  3. 调用SMT求解器

成功标准：

  • 反例被正确识别（34个bug）
  • 等价性被正确证明（77.6%的支持查询）

风险预案：

  • VeriEQL超时 → 报告有界验证结果
  • Mediator返回Unknown → 建议用户用VeriEQL找反例

之所以用"可插拔SQL验证器"子解法，是因为"SQL等价性验证需求"特征。

例子： 论文图4中的SQL和Cypher查询，VeriEQL在2.5秒内找到反例（图3的数据库实例）。

三、子解法的逻辑链（决策树形式）

复制代码 
输入：(Q_G, Q_R, Ψ_G, Ψ_R, Φ)
           │
           ▼
    ┌──────────────────┐
    │ 特征A: 数据模型异构 │
    └────────┬─────────┘
             │
             ▼
    ┌──────────────────────┐
    │ 子解法1: 推断SDT和诱导schema │
    │ InferSDT(Ψ_G) → (Φ_sdt, Ψ'_R) │
    └────────┬─────────────┘
             │
             ▼
    ┌──────────────────┐
    │ 特征B: 路径模式无SQL对应 │
    └────────┬─────────┘
             │
             ▼
    ┌──────────────────────┐
    │ 子解法2: 语法导向翻译    │
    │ Transpile(Q_G) → Q'_R   │
    └────────┬─────────────┘
             │
             ▼
    ┌──────────────────────┐
    │ 特征C: 用户schema≠诱导schema │
    └────────┬─────────────┘
             │
             ▼
    ┌──────────────────────┐
    │ 子解法3: 计算残差转换器   │
    │ Φ[σ] → Φ_rdt           │
    └────────┬─────────────┘
             │
             ▼
    ┌──────────────────────┐
    │ 特征D: 需要验证SQL等价性  │
    └────────┬─────────────┘
             │
             ▼
    ┌────────┴────────┐
    │ 子解法4a或4b选择  │
    ├─────────────────┤
    │ 需要找反例？     │
    │   ├─是→ VeriEQL │
    │   └─否→ Mediator│
    └────────┬────────┘
             │
             ▼
    ┌──────────────────┐
    │ 输出: 等价/不等价/未知 │
    └──────────────────┘

逻辑链类型： 主体是链条结构 （1→2→3→4），在最后一步有分支选择（4a或4b）。

四、隐性方法分析

隐性方法1：中间表示引入法

显性步骤： 论文说"把图查询翻译成SQL，再验证SQL等价性"

隐性关键方法：

当A到B的直接验证太难时，引入中间表示C，使得A→C是正确的（可证明），C→B是已解决的问题。

定义： 间接归约法------通过引入标准中间表示，把异构验证问题归约为同构验证问题。

应用条件：

  • 两个待比较对象属于不同的形式系统
  • 存在一个标准形式，两者都可以映射到该形式
  • 映射本身是可证明正确的

隐性方法2：语义差异的代数分解

显性步骤： Φ r d t = Φ [ σ ] \Phi_{rdt} = \Phi[\sigma] Φrdt=Φ[σ]，其中 σ \sigma σ来自SDT

隐性关键方法：

用户期望的转换 Φ \Phi Φ和标准转换 Φ s d t \Phi_{sdt} Φsdt之间的"差异"可以用简单的语法替换表达。

定义： 转换器分解法------把复杂的跨模型转换分解为"标准转换 + 残差转换"。

公式形式： Φ = Φ s d t ∘ Φ r d t \Phi = \Phi_{sdt} \circ \Phi_{rdt} Φ=Φsdt∘Φrdt

应用条件：

  • 标准转换是well-defined的
  • 残差可以用简单操作（语法替换）计算
  • 分解后的两部分分别比原问题简单

隐性方法3：语义不变性的结构保持

显性步骤： 翻译规则把MATCH→JOIN，OptMatch→LEFT OUTER JOIN

隐性关键方法：

识别两种语言中语义对应的操作符，建立一一映射。

定义： 操作符同态法------找到源语言和目标语言之间的操作符对应关系，使得翻译保持语义。

Cypher操作 SQL操作 语义不变性
MATCH INNER JOIN 无匹配→无结果
OPTIONAL MATCH LEFT OUTER JOIN 无匹配→NULL
WITH 子查询/CTE 中间结果传递
RETURN+AGG GROUP BY 分组聚合

五、隐性特征分析

隐性特征1：变量共享的跨模式传递

问题描述： 在Cypher中，同一个变量可能出现在多个MATCH子句中

cypher 复制代码 
MATCH (c1:CONCEPT)-[:CS]->(p:PA)
WITH p
MATCH (p:PA)-[:SP]->(s:SENTENCE)

隐性特征： 变量p在两个模式中共享，需要在SQL中正确处理。

对应的隐性解法（C-Match2规则的关键步骤）：

  1. 收集两个模式中的变量集合 X 1 X_1 X1和 X 2 X_2 X2
  2. 找到交集 X 1 ∩ X 2 X_1 \cap X_2 X1∩X2
  3. 对交集中的每个变量，生成主键相等的Join条件

之所以需要"变量共享传递"处理，是因为Cypher允许跨模式变量引用，而SQL需要显式的Join条件。

隐性特征2：边的方向性到外键的映射

问题描述： Cypher的边有方向：(a)-[:R]->(b) vs (a)<-[:R]-(b)

隐性特征： 边的方向决定了哪个外键连接哪个节点

对应的隐性解法（PT-Path规则）：

  • 方向→：fk_s连源节点，fk_t连目标节点
  • 方向←：反过来
  • 方向↔：需要UNION或OR条件

隐性特征3：聚合语义的分组键推断

问题描述： Cypher的RETURN可以混合聚合和非聚合表达式

cypher 复制代码 
RETURN m.dname, Count(n)

隐性特征： 非聚合表达式隐式成为分组键

对应的隐性解法（Q-Agg规则）：

  1. 检测表达式列表中是否有聚合函数
  2. 用filter(λx.¬IsAgg(x), E')提取非聚合表达式
  3. 非聚合表达式作为GROUP BY的分组键

六、方法的潜在局限性

局限性1：Cypher子集的限制

不支持的特性：

  • 变长路径查询：MATCH (a)-[:R*1..5]->(b)
  • 最短路径：shortestPath((a)-[:R*]->(b))
  • 图可达性原语

根本原因： 这些特性在核心SQL中没有对应物（需要递归CTE）

影响范围： 论文评估中所有benchmark都在支持范围内，但实际应用可能受限

局限性2：验证器能力的限制

VeriEQL的局限：

  • 只能有界验证，不能证明等价
  • 可能遗漏需要大数据集才能暴露的bug（实验中2/50的漏报）

Mediator的局限：

  • 不支持聚合和外连接
  • 复杂Join链可能导致超时（14/42超时）
  • 需要推断复杂的bisimulation不变式

局限性3：转换器语言的表达能力

当前限制：

  • 只支持简单的谓词映射规则
  • 不支持条件分支、算术运算

潜在问题：

  • 复杂的schema重构（如表拆分、列合并）可能无法表达
  • 需要用户手动简化schema映射

局限性4：性能开销

翻译开销： 平均6.3ms（可忽略）

验证开销：

  • VeriEQL平均23.4秒找反例
  • Mediator平均16.8秒完成验证

执行开销： 翻译出的SQL有15.6%超过1.2x减速

七、多题一解与一题多解

多题一解：跨模型等价验证的通用思路

共用特征： 两种数据模型之间存在结构对应关系

共用解法： 间接归约法（引入标准中间表示）

适用问题类型：

  1. SQL方言之间的等价验证（MySQL vs PostgreSQL）
  2. NoSQL与SQL之间的等价验证
  3. 不同图查询语言之间的等价验证（Cypher vs SPARQL vs GQL）
  4. 程序变换的正确性验证

识别标志：

  • 两种语言/模型语法不同但语义可对应
  • 存在标准化的中间表示
  • 单边验证工具已成熟

一题多解：Cypher-SQL等价验证的不同路径

解法 对应特征 优缺点
本文方法（归约到SQL） 利用SQL工具成熟 可复用，但受限于SQL工具能力
直接SMT编码 需要完整验证 灵活，但需要从零构建
随机测试 快速找bug 快速，但不能证明等价
交互式证明 需要高置信度 严格，但需要人工介入

八、暴露的决策过程：尝试过但放弃的方案

放弃方案1：直接SMT编码

尝试动机： 最直接的方法，把图查询和SQL查询都编码成SMT公式

放弃原因：

"directly reasoning about equivalence...would require complex SMT encodings that combine graph and relational structures"

具体困难：

  • 需要同时编码节点/边语义和表/行语义
  • 量词结构复杂（图的模式匹配需要存在量词嵌套）
  • 没有现成工具可复用

放弃方案2：完全依赖用户提供映射

尝试动机： 用户最了解自己的schema，让用户写完整映射

放弃原因：

  • 用户工作量大
  • 容易写错
  • 需要验证映射本身的正确性

最终折中： 用户只需提供 Φ \Phi Φ（图→目标关系schema），SDT和RDT自动推导

放弃方案3：只使用一种验证后端

尝试动机： 简化实现

放弃原因：

  • VeriEQL不能证明等价，只能找反例
  • Mediator不支持聚合，覆盖面不足
  • 两者互补，组合使用效果更好

九、隐蔽知识

新手注意不到的规律

规律1： 图数据库的"边表"总是需要两个外键

初学者可能以为边只是源节点到目标节点的指针，但在关系表示中，需要显式的外键约束来保证引用完整性。

规律2： Cypher的隐式分组 vs SQL的显式GROUP BY

Cypher允许RETURN a, Count(b)而不写GROUP BY，但翻译到SQL时必须显式添加。

规律3： Optional Match的NULL语义

OPTIONAL MATCH不只是"可能匹配"，而是"无匹配时用NULL填充"，这与LEFT OUTER JOIN的语义完全一致。

新手无法觉察的微小区别

区别1： 图4中SQL和Cypher查询的Count差异

SQL数的是满足条件的Sp表行数，Cypher数的是路径数。由于一个PA可能连接多个Sp，结果不同。

区别2： 主键 vs 默认属性键

图数据库的"默认属性键"概念与关系数据库的"主键"相似但不完全相同------图数据库可能允许没有默认键的节点。

区别3： 变量作用域

Cypher的WITH子句会"切断"变量作用域，只有显式传递的变量才能在后续子句中使用。翻译时需要正确处理投影。

对意外的敏感

意外1： 官方教程竟然有bug

大多数人会假设官方文档是正确的，但作者验证了Neo4j官方教程的例子，发现了语义不等价的情况。这体现了对"权威来源也可能出错"的敏感。

意外2： 人工翻译的错误率与GPT相当

直觉上人工翻译应该比GPT更可靠，但实验表明人工翻译也有4/160（2.5%）的错误率，这说明问题的复杂性超出预期。

意外3： 翻译出的SQL有时比手写的更快

反直觉的是，33.3%的情况下自动翻译的SQL执行更快。原因可能是翻译出的SQL更规范，更容易被数据库优化器优化。

十、总结：解法的本质结构

c 复制代码 
问题本质：异构系统的语义比较
           │
           ▼
核心洞察：两个异构系统存在共同的语义基础（路径≈Join）
           │
           ▼
解法策略：引入标准中间表示，归约到同构比较
           │
           ├──→ 子解法1：定义标准表示（SDT）
           ├──→ 子解法2：翻译到标准表示（语法导向翻译）
           ├──→ 子解法3：对齐目标表示（RDT）
           └──→ 子解法4：复用成熟工具（SQL验证器）
           │
           ▼
关键隐性方法：间接归约、转换器分解、操作符同态
           │
           ▼
适用范围：所有存在语义对应关系的异构系统验证问题
相关推荐
SoleMotive.3 小时前
redis和mysql有什么区别，以及redis和mysql都有什么缺点，以及什么地方redis不如mysql？
数据库·redis·mysql
代码代码快快显灵3 小时前
Android跨应用数据共享：ContentProvider详解
jvm·数据库·oracle
聪明努力的积极向上3 小时前
【MYSQL】IN查询优化
数据库·mysql
济南java开发,求内推3 小时前
MongoDB: 升级版本至：5.0.28
数据库·mongodb
小灰灰搞电子3 小时前
Qt PDF模块详解
数据库·qt·pdf
老华带你飞3 小时前
健身房预约|基于springboot 健身房预约小程序系统(源码+数据库+文档)
java·数据库·vue.js·spring boot·后端·小程序
梁萌3 小时前
MySQL主从数据同步实战
数据库·mysql
嘻哈baby3 小时前
MySQL主从复制与读写分离实战指南
数据库·mysql·adb
一水鉴天4 小时前
整体设计 定稿 之 5 讨论问题汇总 和新建 表述总表/项目结构表 文档分析，到读表工具核心设计讨论（豆包助手）
数据库·人工智能·重构
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser08【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）09BongoCat - 跨平台键盘猫动画工具10安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）