论文题目:Tight and Efficient Upper Bound on Spectral Norm of Convolutional Layers(卷积层谱范数的紧凑高效上界)
会议:ECCV2024
摘要:控制与卷积运算相关的雅可比矩阵的谱范数可以提高cnn的泛化、训练稳定性和鲁棒性。计算范数的现有方法要么倾向于高估范数,要么随着输入和内核大小的增加,它们的性能可能会迅速下降。在本文中,我们证明了四维卷积核的谱范数的张量版本,直到一个常数因子,作为与卷积运算相关的雅可比矩阵的谱范数的上界。这个新的上界与输入图像分辨率无关,是可微的,可以在训练过程中有效地计算出来。通过实验,我们展示了如何使用这个新的边界来提高卷积架构的性能。
源码地址:https://github.com/GrishKate/conv_norm.
深入理解卷积层谱范数的高效计算
引言
在深度学习中,控制神经网络的Lipschitz常数是一个重要课题。它直接关系到模型的鲁棒性、泛化能力和训练稳定性。对于卷积神经网络而言,这个问题归结为如何高效计算卷积层Jacobian矩阵的谱范数(即最大奇异值)。
ECCV 2024收录的这篇论文提出了一种基于张量范数的新方法,在保持计算效率的同时显著提升了估计精度。
背景:为什么谱范数很重要?
神经网络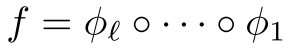 的Lipschitz常数可以用各层Lipschitz常数的乘积来界定:
的Lipschitz常数可以用各层Lipschitz常数的乘积来界定:
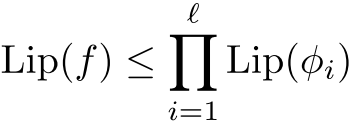
对于线性层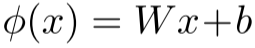 ,其Lipschitz常数等于权重矩阵的谱范数
,其Lipschitz常数等于权重矩阵的谱范数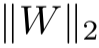 。控制这个值可以防止梯度爆炸、提高对抗鲁棒性、改善泛化性能。
。控制这个值可以防止梯度爆炸、提高对抗鲁棒性、改善泛化性能。
然而,卷积层的Jacobian矩阵是一个巨大的(双重块)Toeplitz矩阵。以一个典型的卷积层为例:输入 256尺寸的图像、64个通道,其Jacobian矩阵尺寸达到 4.2×4.2×10^12,直接计算SVD完全不现实。
现有方法的困境
学术界提出了多种方法来解决这个问题:
依赖输入尺寸的方法 :幂迭代法通过反复应用卷积操作来逼近最大奇异值。虽然准确,但复杂度为 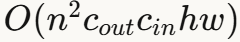 ,对高分辨率图像或3D卷积代价过高。
,对高分辨率图像或3D卷积代价过高。
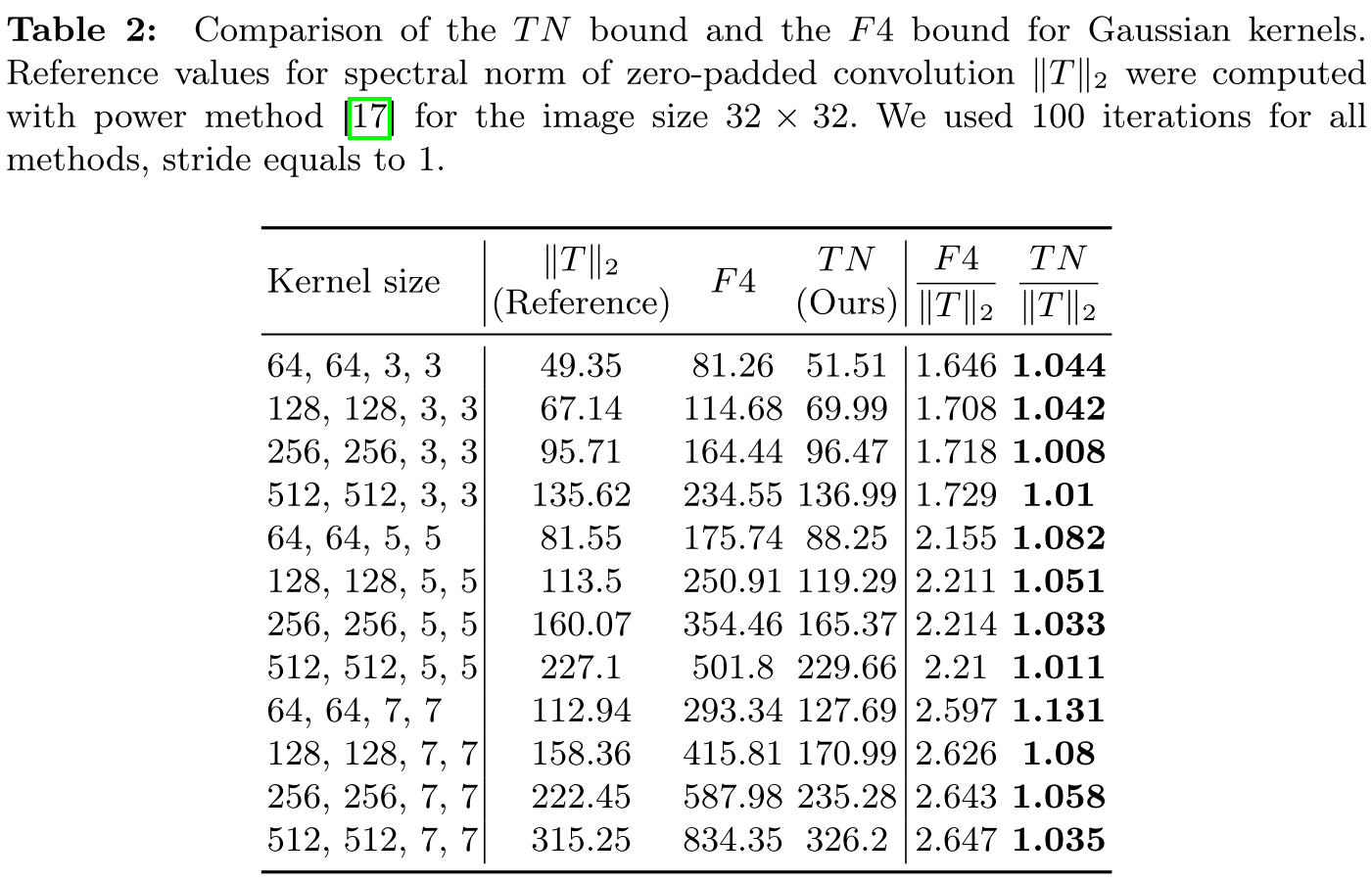
F4方法 :Singla和Feizi提出使用卷积核四种展开矩阵谱范数的最小值乘以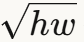 作为上界。这个方法不依赖输入尺寸,但实验显示它会高估真实值1.7-2.6倍。
作为上界。这个方法不依赖输入尺寸,但实验显示它会高估真实值1.7-2.6倍。
本文方法:张量谱范数
论文的核心洞察是:将四维卷积核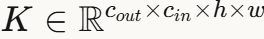 视为一个张量,其作为多线性泛函的范数(张量谱范数)可以用来精确界定卷积的谱范数。
视为一个张量,其作为多线性泛函的范数(张量谱范数)可以用来精确界定卷积的谱范数。
张量谱范数的定义:
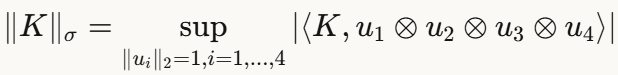
这个定义是矩阵谱范数向高维的自然推广。
主定理证明了双向界:
- 下界
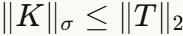 :通过观察卷积核的某个展开矩阵是Jacobian矩阵T的子矩阵
:通过观察卷积核的某个展开矩阵是Jacobian矩阵T的子矩阵 - 上界
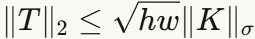 :通过谱密度矩阵的技术,将Jacobian的谱范数与张量的多线性形式联系起来
:通过谱密度矩阵的技术,将Jacobian的谱范数与张量的多线性形式联系起来
一个关键的技术点是:证明过程中需要在复数域上取上确界。作者在附录中给出了反例,说明如果只在实数域上优化,上界可能不成立。
高效计算:HOPM算法
张量谱范数可以通过**高阶幂方法(HOPM)**高效计算。算法思想是:固定其他向量,依次对每个向量求解最优值,这等价于求解最佳秩1近似问题。

# HOPM算法伪代码
for iteration in range(n_iters):
u1 = contract(K, [I, u2, u3, u4]) # 对第一个维度收缩
u1 = conj(u1) / norm(u1) # 归一化(注意共轭)
# 类似更新 u2, u3, u4
return abs(contract(K, [u1, u2, u3, u4]))每次迭代的复杂度为 O(c_{in}c_{out}hw),与图像分辨率完全无关。训练时,由于权重变化缓慢,可以利用上一步的向量作为初始值,仅需一次迭代即可更新。
为什么比F4更精确?
F4方法使用四种特定展开矩阵的最小谱范数。而根据张量理论中的一个基本引理:张量谱范数不超过其任何展开矩阵的谱范数。
这意味着:
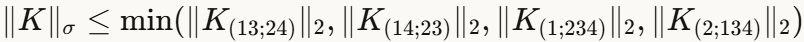
因此,TN bound在理论上必然不劣于F4 bound,实验也验证了这一点。
实验亮点
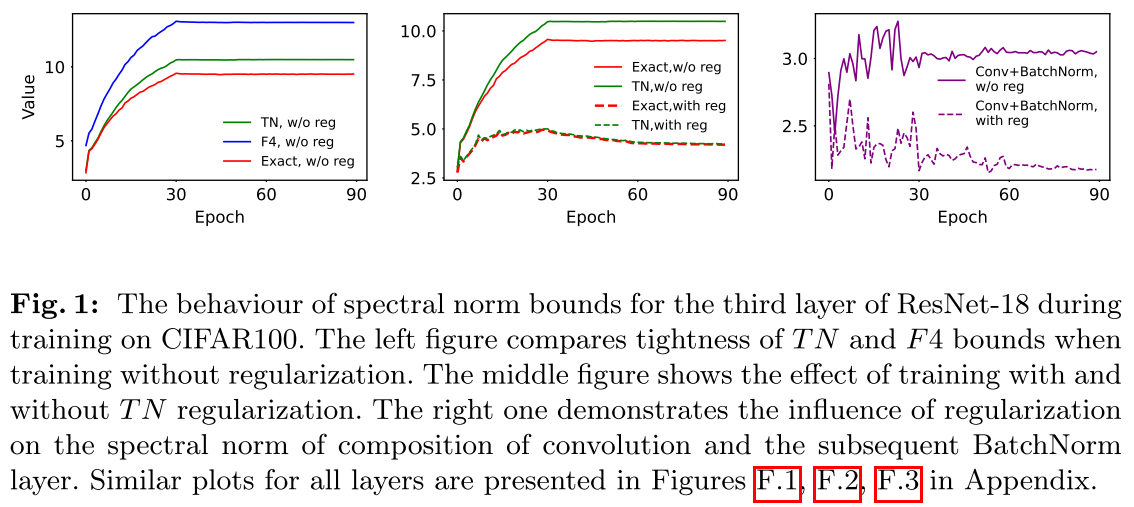
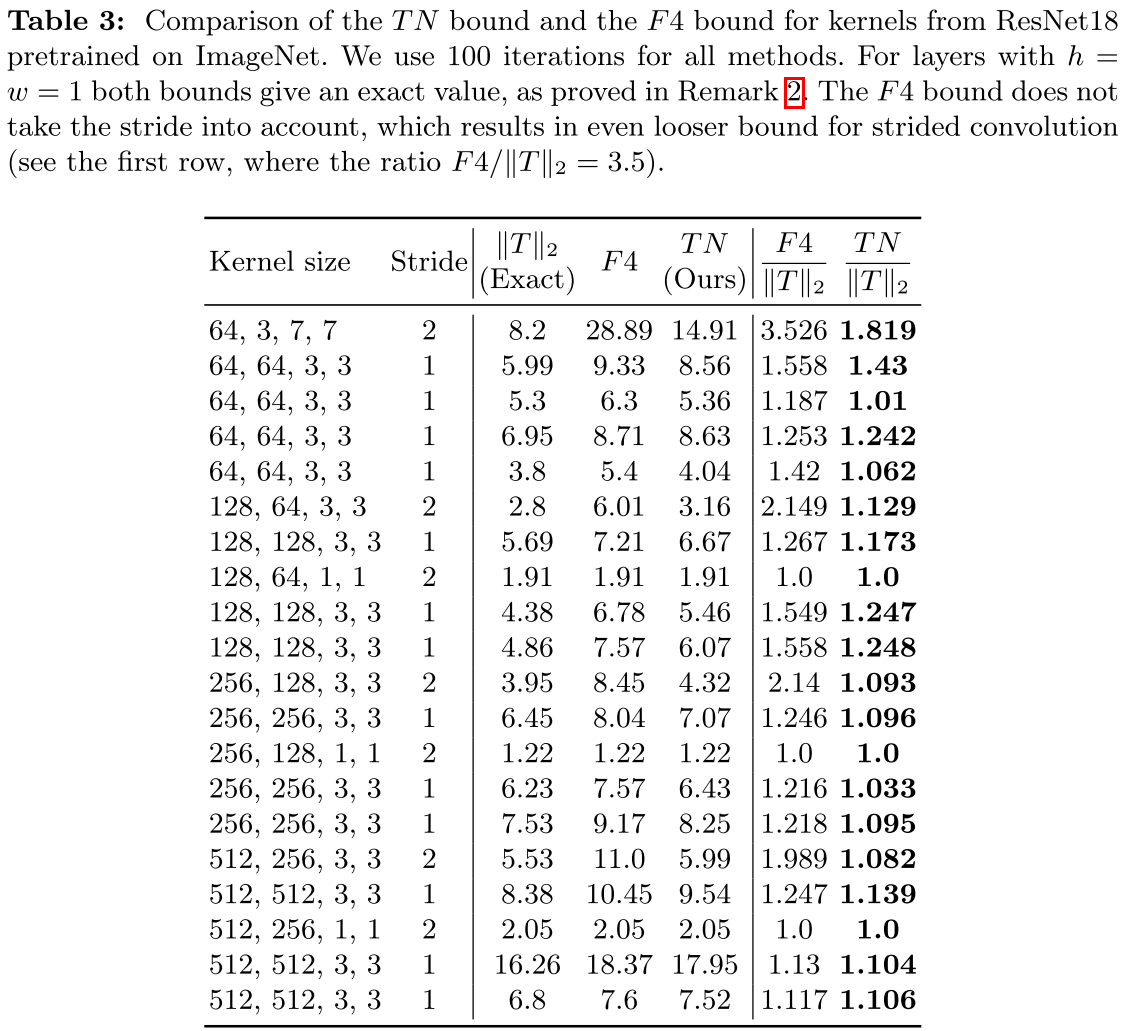
精度验证:在预训练的ResNet18上,TN bound对大多数层的估计误差在10%以内,而F4误差通常在20%-50%。对于步长卷积,差距更加明显。
正则化应用:将所有卷积层谱范数之和作为正则项加入损失函数:
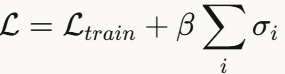
这种简单的正则化策略在CIFAR100和ImageNet上都取得了一致的精度提升,且几乎不增加训练时间。
正交正则化:论文还提出了两种新的正交正则化方法:
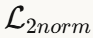 :基于卷积核与自身卷积后的张量谱范数
:基于卷积核与自身卷积后的张量谱范数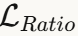 :谱范数与Frobenius范数的比值(当所有奇异值相等时达到最小)
:谱范数与Frobenius范数的比值(当所有奇异值相等时达到最小)
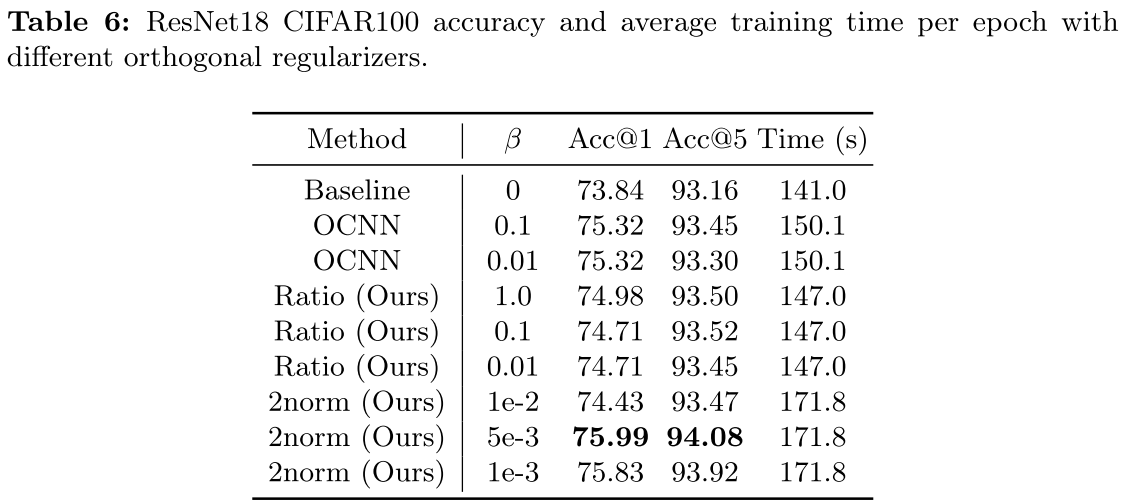
其中 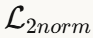 在CIFAR100上将准确率从73.84%提升到75.99%,效果显著。
在CIFAR100上将准确率从73.84%提升到75.99%,效果显著。


局限性与展望
尽管TN bound在理论和实践上都有明显优势,但仍存在改进空间。最坏情况下,TN bound仍可能高估真实值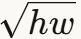 倍(虽然实验中通常远小于这个值)。对于非常大的核尺寸,这个差距可能变得显著。
倍(虽然实验中通常远小于这个值)。对于非常大的核尺寸,这个差距可能变得显著。
此外,HOPM算法只能保证收敛到局部最优。虽然通过多次随机初始化可以缓解这个问题,但全局最优性没有理论保证。
总结
这篇论文为卷积层谱范数的计算提供了一个优雅的解决方案。通过将问题转化为张量谱范数的计算,作者在不牺牲效率的前提下显著提升了估计精度。这个结果不仅有理论美感(张量范数是矩阵范数的自然推广),也有实际价值(可以更精确地控制神经网络的Lipschitz常数)。
对于关注模型鲁棒性、泛化性和训练稳定性的研究者和工程师,这篇论文提供了一个即插即用的工具。
论文比较偏数学内容,主要解析由AI整理而成,如果大家想更深入了解,请阅读原文噢~