【c++知识铺子】封装map和set（详细版）

爱装代码的小瓶子2025-12-17 12:14

关注我，学习c++不迷路:

个人主页：爱装代码的小瓶子

专栏如下：

  1. c++学习
  2. Linux学习

后续会更新更多有趣的小知识，关注我带你遨游知识世界

期待你的关注。

文章目录

  • [1. 前言：](#1. 前言：)
  • [2. 重新设计结构：](#2. 重新设计结构：)
    • [2-1 节点设计：](#2-1 节点设计：)
    • [2-2 迭代器设计：](#2-2 迭代器设计：)
  • [3. 完善迭代器:](#3. 完善迭代器:)
    • [3-1 operator``++``：](#3-1 operator++：)
    • [3-2 operator``--``](#3-2 operator--)
  • [4. 主干设计Tree部分：](#4. 主干设计Tree部分：)
  • [6. 开始封装map和set：](#6. 开始封装map和set：)
  • [7. 总结：](#7. 总结：)

1. 前言：

我们之前已经学习了如何设计并且写出红黑树，这次我们需要利用这些来封装出一个红黑树。

在我们的红黑树中是没有实现迭代器，在这里面我们需要实现，同时我们还需要设计使红黑树同时能满足set和map，其中set是一个key，而map是key和val，我们需要怎么设计才能满足这个条件呢？

不妨来看看SGI中的STL是怎么设计的：

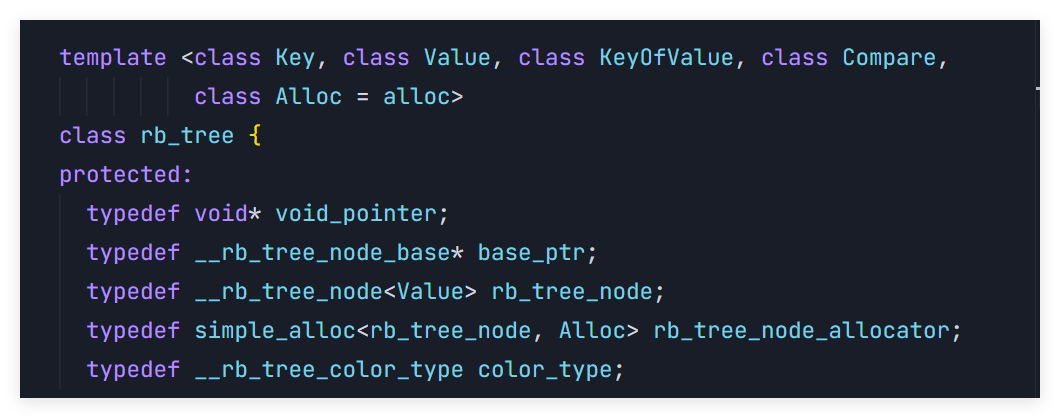
在这里面，我们的模板不再简单的是：

源码中传入传入了类型key和val以及两个仿函数。这两个函数一个是用于不同类型的比较。另一个则是来满足set和map的不同。

  • Key ：键类型
  • Value ：值类型
  • KeyOfValue ：从Value中提取Key的函数对象
  • Compare ：键值比较函数对象
  • Alloc ：内存分配器。

在stl_set.h中设计成这样：

我们发现，key既是key_type也是value_type。这样就也满足了占位，但是如果是map，传入了pair，如何取到pair的first，这个就要讲到后面的KeyOfValue。

这里就讲述了是怎么面对不同的数据类型来做不同的做取值的，这里可能讲的不清楚，但是没事。后面我们还会详细的讲讲。

2. 重新设计结构：

2-1 节点设计：

我们为了与stl保持高度一致，我们也采取差不多的设计，那么我们原本的节点也需要改变：我们节点只有一个类型就是T，无论传入的是key，还是pair<K,V>；都只给一个名字叫T：

cpp 复制代码 
enum Color {
	BLACK,
	RED,
};
template<class T>
class RBTreeNode {
public:
	RBTreeNode(const T& date)
		:_date(date)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
	{ }

	T _date;
	RBTreeNode<T>* _parent;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	Color _col;
};

这样一个节点就好了，后续只需连接或者插入就可以满足红黑树，同时为了满足迭代器，还要传入的参数，也要改变：

cpp 复制代码 
template<class K, class T, class KeyOfT>
class RBTree {
	using Node = RBTreeNode<T>;
public:
	using Iterator = RBTreeIterator<T, const T&, T*>;
	using constIterator = RBTreeIterator<T, const T&,T*>;
	Node* _root = nullptr;
};

里面也对外公开了迭代器，同时模板也不再是简单的<K,V>结构了，这里是key和T结构。T可以是后面传入的key，也可以是pair<K,V>。

2-2 迭代器设计：

在stl中，迭代器传入了三个参数，这些都是为了迭代器后续的实现完成的，这些操作使得迭代器可以像指针一样使用，同时提供了类型安全和容器无关的统一接口。

  1. Value参数
    • 作用 ：表示迭代器指向的元素类型
    • 用途 ：定义了迭代器所操作的值的类型
    • 示例 ：在红黑树中，Value可能是 int 、 pair<const int, string> 等
    1. Ref参数
    • 作用 ：表示迭代器解引用后返回的引用类型
    • 用途 ：控制迭代器返回的是可修改引用还是只读引用
    • 示例 ：
      • 对于普通迭代器： Ref = Value& （可修改引用）
      • 对于常量迭代器： Ref = const Value& （只读引用）
  1. Ptr参数
    • 作用 ：表示迭代器通过 -> 操作符返回的指针类型
    • 用途 ：控制迭代器返回的指针类型
    • 示例 ：
      • 对于普通迭代器： Ptr = Value* （可修改指针）
      • 对于常量迭代器： Ptr = const Value* （只读指针）
        那么遵循这种结构，我们也可以来尝试实现这种结构吧：
        //开始封装迭代器,里面是节点。
cpp 复制代码 
template<class T, class Ref, class Ptr>
class RBTreeIterator {
	using Node = RBTreeNode<T>;
	using Self = RBTreeIterator<T, Ref, Ptr>;
	private:
		Node* _node;
		Node* _root;
};

这里还要_root是后面需要使用的。

3. 完善迭代器:

在我们设计的迭代器还少了很多主要功能比如++和- -，我来尝试实现：

3-1 operator++：

我们可以看看节点是如何进入下一个节点的，在红黑树中，我们是按照左中右来遍历的，那么我们可以总结出：

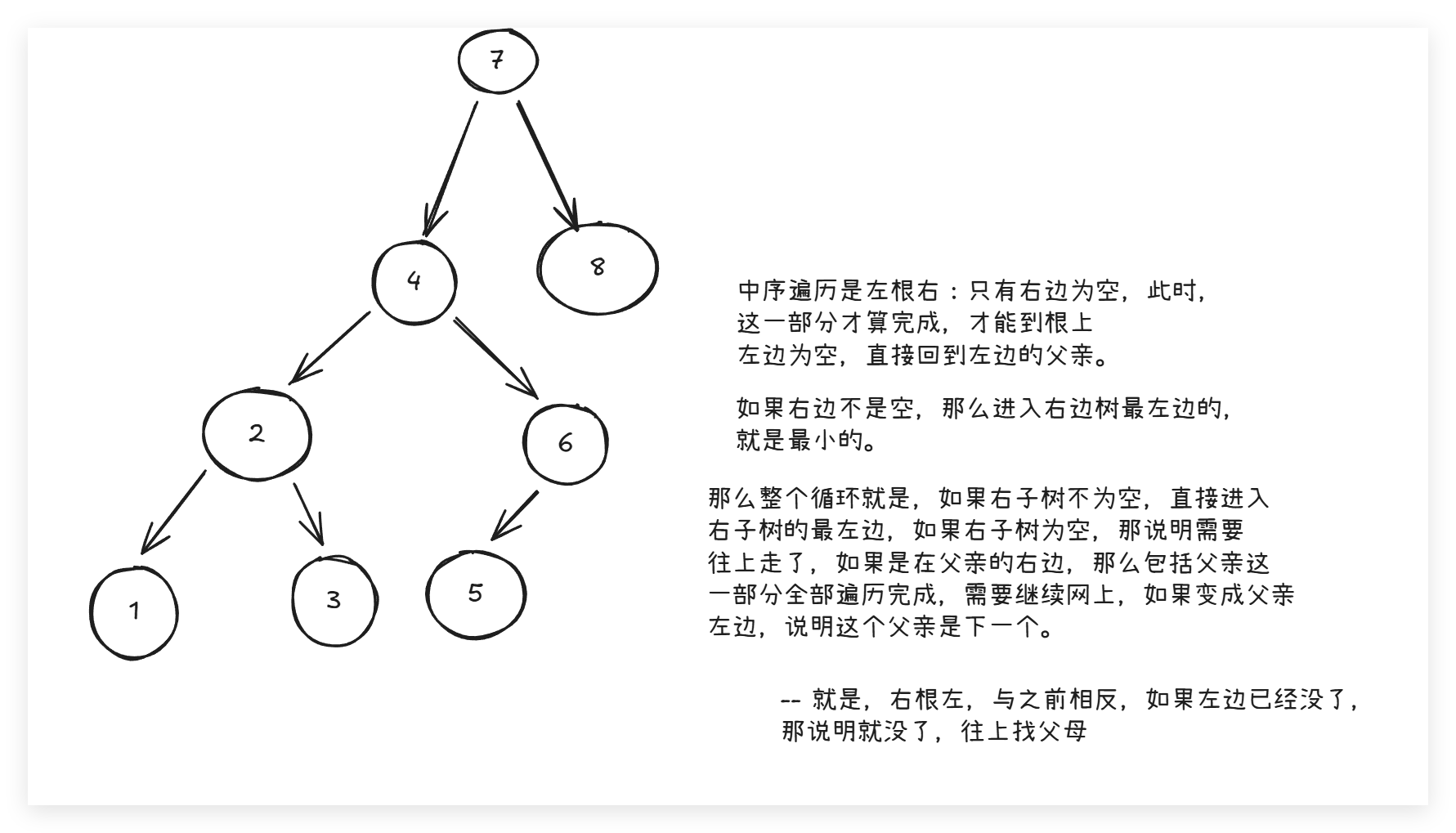
那么我们就有：

cpp 复制代码 
	Self operator++()
	{
		if (_node->_right)
		{
			//如果右边不是空的，说明下一个节点就是右子树最小的即最左边的
			Node* min = _node->_right;
			while (min->_left)
			{
				min = min->_left;
			}
			_node = min;
		}
		else {
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}

这就是加加的逻辑。完成++。

3-2 operator--

--的逻辑与这个大致相似，但是不同的是：如何从空节点回到最后也是end（）节点呢？

这里就用到了_root.利用这个找到这个end节点就是最右边的节点：

cpp 复制代码 
	Self operator--()
	{
		if (_node == nullptr)
		{
			Node* rootMax = _root;
			while (rootMax && rootMax->_right)
			{
				rootMax = rootMax->_right;
			}
			_node = rootMax;
		}
		if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_left)
			{
				max = max->_right;
			}
			_node = max;
		}
		else {
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && cur == parent->left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}

但是我们在运行时很快就发现了这个错误：

错误 1：operator-- 的逻辑穿透（致命）

现象：当迭代器为 end() 时，你找到了最大节点 rootMax，但没有返回。代码会继续向下执行，导致逻辑混乱。

修正：处理完 end() 情况后，必须立即 return *this;。

cpp 复制代码 
Self operator--()
{
	if (_node == nullptr)
	{
		Node* rootMax = _root;
		while (rootMax && rootMax->_right)
		{
			rootMax = rootMax->_right;
		}
		_node = rootMax;
		return *this;
	}
	if (_node->_left)
	{
		Node* max = _node->_left;
		while (max->_right)
		{
			max = max->_right;
		}
		_node = max;
	}
	else {
		Node* cur = _node;
		Node* parent = _node->_parent;
		while (parent && cur == parent->_left)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_node = parent;
	}
	return *this;
}

这样就完成了大致的逻辑。

4. 主干设计Tree部分：

4-1 新加部分：

在之前的部分，我么便可以尝试提供迭代器的接口，分别是：begin和end。

  1. 在这里begin就是最小的，那么就是左子树最左边的，同时防止数为空导致空指针解引用。
  2. end则比较简单，只需传入空即可。
  3. 需要给出两部分迭代器，一个常性迭代器，一个正常的
cpp 复制代码 
	Iterator begin()
	{
		Node* cur = _root;
		if (_root == nullptr)
			return end();  // 空树时直接返回 end()
		while (cur->_left)
		{
			cur = cur->_left;
		}
		return Iterator(cur,_root);
	}

	constIterator begin()const
	{
		Node* cur = _root;
		if (_root == nullptr)
			return end();
		while (cur->_left)
		{
			cur = cur->_left;
		}
		return constIterator(cur, _root);
	}

	Iterator end()
	{
		return Iterator(nullptr, _root);
	}

	constIterator end() const
	{
		return Iterator(nullptr, _root);
	}

4-2改变部分：

这里大部分逻辑不变，但是由于前面的变量发生改变，所以发生改变：

cpp 复制代码 
	pair<Iterator,bool> insert(const T& date)
	{
		if (_root == nullptr)
		{
			_root = new Node(date);
			_root->_col = BLACK;
			return { Iterator(_root,_root),true };
		}
		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(date) > kot(cur->_date))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(date) < kot(cur->_date))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return {Iterator(cur,_root),false};
		}

		cur = new Node(date);
		if (kot(date) < kot(parent->_date))
			parent->_left = cur;
		else
			parent->_right = cur;
		Node* NewNode = cur;
		cur->_col = RED;//默认插入为红色，如果插入黑色不满足红黑树
		cur->_parent = parent;

		//开始分类讨论：
		while (parent && parent->_col == RED)
		{
			Node* Gparent = parent->_parent;
			//如果父亲不是空并且父亲为红色就进入循环：
			if (Gparent->_left == parent)
			{
				//   G
				// p   u
				Node* uncle = Gparent->_right;
				if (uncle && uncle->_col == RED )
				{
					//开始变色：
					uncle->_col = BLACK;
					parent->_col = BLACK;
					Gparent->_col = RED;//注意事项

					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					//这里uncle不可能是黑色的，如果parent是红色的，那么uncle如果存在，就必须是红色的
					//  G
					//p   
					if (cur == parent->_left)
					{
						//    G
						//  p
						//c
						RotateR(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else if (cur == parent->_right)
					{
						//    G
						//  p
						//   c
						RotateL(parent);
						RotateR(Gparent);
						Gparent->_col = RED;
						cur->_col = BLACK;//cur做了Gpa
					}
					//这里需不要break?之前需要更新是因为Gpanet的parent可能也是红色
					break;
				}
			}
			else {
				//   G
				//u     P
				Node* uncle = Gparent->_left;
				if (uncle && uncle->_col == RED)
				{
					//开始变色：
					uncle->_col = parent->_col = BLACK;
					Gparent->_col = RED;
					cur = Gparent;
					parent = cur->_parent;
				}
				else {
					if (cur == parent->_right)
					{
						//  G
						//   p
						//      c
						RotateL(Gparent);
						parent->_col = BLACK;
						Gparent->_col = RED;
					}
					else {
						RotateR(parent);
						RotateL(Gparent);
						cur->_col = BLACK;
						Gparent->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;//无论如何都要让_root变成黑色
		return {Iterator(NewNode,_root),true};
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* Pparent = parent->_parent;

		//第一步：处理subLR
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		//第二部处理：parent
		subL->_right = parent;
		parent->_parent = subL;
		//第三部处理Pparent和 subL
		subL->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subL;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subL;
			else 
				Pparent->_right = subL;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* Pparent = parent->_parent;

		//1.处理：subRL 
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		//2.处理：parent
		parent->_parent = subR;
		subR->_left = parent;
		//3.处理Pparent和subR；
		subR->_parent = Pparent;
		if (Pparent == nullptr)
			_root = subR;
		else {
			if (parent == Pparent->_left)
				Pparent->_left = subR;
			else
				Pparent->_right = subR;
		}
	}

	void Inorder()
	{
		_Inorder(_root);
	}

	Node* Find(const T& date)
	{
		KeyOfT kot;
		if (_root == nullptr)
			return nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(date) > kot(cur->_date))
				cur = cur->_right;
			else if (kot(date) < kot(cur->_date))
				cur = cur->_left;
			else
				return cur;
		}
		return nullptr;
	}

	bool IsRBTree()
	{
		//可以直接判断，就直接在这里写：
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;
		int RefNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				RefNum++;
			cur = cur->_left;
		}
		return _Check(_root, 0, RefNum);
	}

	size_t Size()
	{
		return _Size(_root);
	}

	size_t Height()
	{
		return _Height(_root);
	}


private:
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_date << endl;
		_Inorder(root->_right);
	}

	bool _Check(Node* root, int BH, int RN)
	{
		if (root == nullptr)
		{
			if (BH != RN)
			{
				cout << "存在黑色结点的数量不相等的路径" << endl;
				return false;
			}
			return true;//控制递归返回条件。
		}
		if (root->_col == BLACK)
			BH++;
		if (root->_col == RED && root->_parent->_col == RED)
		{
			//如果是根节点，是不会找他的父节点，就不会空指针的解引用
			cout << "存在两个红色节点" << endl;
			return false;
		}
		return _Check(root->_left, BH, RN) && _Check(root->_right, BH, RN);
	}

	size_t _Size(Node* root)
	{
		if (root == nullptr)
			return 0;
		//没遍历一个都会加1.
		return _Size(root->_left) + _Size(root->_right) + 1;
	}

	//size_t _Height(Node* root)
	//{
	//	if (root == nullptr)
	//		return 0;
	//	size_t LH = _Height(root->_left);
	//	size_t RH = _Height(root->_right);
	//	return 1 + max(LH, RH);
	//}
		
	size_t _Height(Node* root)
	{
		queue<Node*> q;
		q.push(root);
		size_t height = 0;
		while (!q.empty())
		{
			height++;
			//如果不为空
			size_t size = q.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = q.front();
				if(node->_left)
					q.push(node->_left);
				if(node->_right)
					q.push(node->_right);
				q.pop();
			}
		}
		return height;
	}
	Node* _root = nullptr;
};

6. 开始封装map和set：

6-1set：

终于写到这里了，我们在这里开始封装：

先写setofKey，取出类型里面的key，在这里我们就有：

cpp 复制代码 
	template<class K>
	class set {
		struct SetOfT {
			const K& operator()(const K& key)
			{
				return key;
				//如果是set ,那么就放回set的关键词key
			}
		};
  • RBTree<K, const K, SetOfT> 的第三个模板参数通常表示"如何从节点存储的值取出用于比较的键"。对 map 会是取 pair.first，对 set 就是"值自身"。
  • SetOfT::operator()(const K& key) 做的就是恒等映射------接收一个 K 的引用并返回同一个 K 的 const 引用，避免不必要的拷贝。
  • 返回 const K& 的前提是调用方把一个有效的 K 实例（通常是节点内存储的值）以引用传入，返回的引用仍然有效。千万不要返回指向局部临时对象的引用

同时开始封装各种接口：

cpp 复制代码 
	public:
		using iterator = RBTree<K, const K, SetOfT>::Iterator;
		using const_iterator = RBTree<K, const K, SetOfT>::constIterator;
		iterator begin()
		{
			return _t.begin();
		}

		const_iterator begin()const
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator end()const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const K& key)
		{
			return _t.insert(key);
		}


		size_t height()
		{
			return _t.Height();
		}

		void Inorder()
		{
			_t.Inorder();
		}

	private:
		RBTree<K, const K, SetOfT> _t;
	};

}
cpp 复制代码 
#pragma once
#include"RBTree.h"

namespace wwh{

	template<class K>
	class set {
		struct SetOfT {
			const K& operator()(const K& key)
			{
				return key;
				//如果是set ,那么就放回set的关键词key
			}
		};
	public:
		using iterator = RBTree<K, const K, SetOfT>::Iterator;
		using const_iterator = RBTree<K, const K, SetOfT>::constIterator;
		iterator begin()
		{
			return _t.begin();
		}

		const_iterator begin()const
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator end()const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const K& key)
		{
			return _t.insert(key);
		}


		size_t height()
		{
			return _t.Height();
		}

		void Inorder()
		{
			_t.Inorder();
		}

	private:
		RBTree<K, const K, SetOfT> _t;
	};

}

6-2 map：

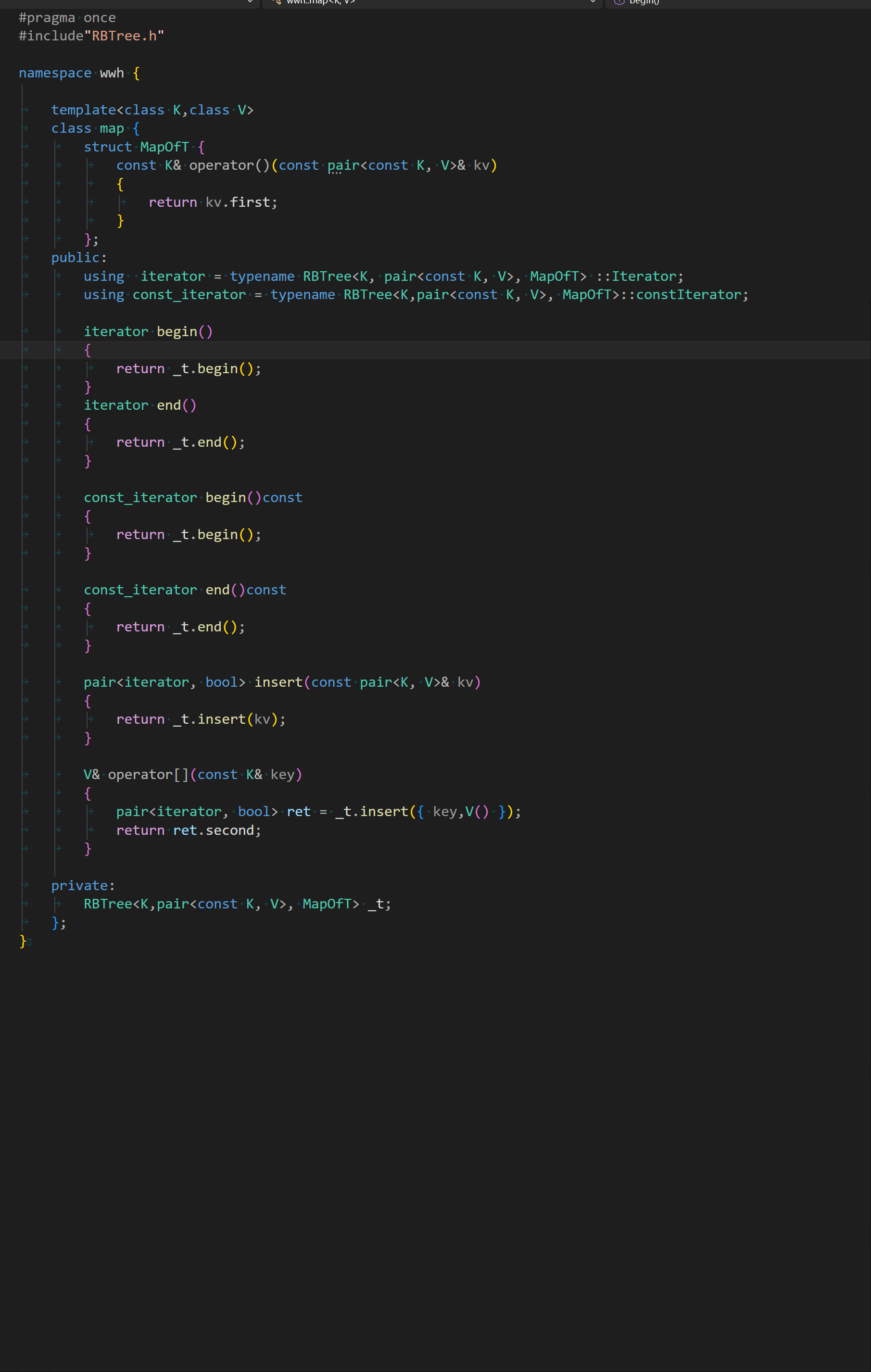
与set相似，我们这里也准备了mapofkey：

cpp 复制代码 
	template<class K,class V>
	class map {
		struct MapOfT {
			const K& operator()(const pair<const K, V>& kv)
			{
				return kv.first;
			}
		};

后面完成封装：

cpp 复制代码 
#pragma once
#include"RBTree.h"

namespace wwh {

	template<class K,class V>
	class map {
		struct MapOfT {
			const K& operator()(const pair<const K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		using  iterator = typename RBTree<K, pair<const K, V>, MapOfT> ::Iterator;
		using const_iterator = typename RBTree<K,pair<const K, V>, MapOfT>::constIterator;

		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}

		const_iterator begin()const
		{
			return _t.begin();
		}

		const_iterator end()const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = _t.insert({ key,V() });
			return ret.second;
		}

	private:
		RBTree<K,pair<const K, V>, MapOfT> _t;
	};
}

7. 总结：

最好我们来测试一下：

相关推荐
2201_757830872 小时前
tlias的部门的增删改查操作
java·开发语言
明洞日记2 小时前
【VTK手册026】高性能网格简化——vtkQuadricClustering 深度解析
c++·图像处理·vtk·图形渲染
私人珍藏库2 小时前
AutoGLM无需豆包手机，让AI自动帮你点外卖-刷视频
android·ai·智能手机·工具·软件·辅助·autoglm
雨雨雨雨雨别下啦3 小时前
Spring AOP概念
java·后端·spring
on the way 1233 小时前
day04-Spring之Bean的生命周期
java·后端·spring
代码笔耕3 小时前
面向对象开发实践之消息中心设计（二）
java·后端·架构
xiaoye-duck3 小时前
C++入门基础指南：引用全解析（从入门到精通）
c++
XFF不秃头3 小时前
力扣刷题笔记-下一个排列
c++·笔记·算法·leetcode
要开心吖ZSH3 小时前
应用集成平台-系统之间的桥梁-思路分享
java·kafka·交互
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser08BongoCat - 跨平台键盘猫动画工具09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）