160.相交链表 - 技术栈

思路

暴力法:

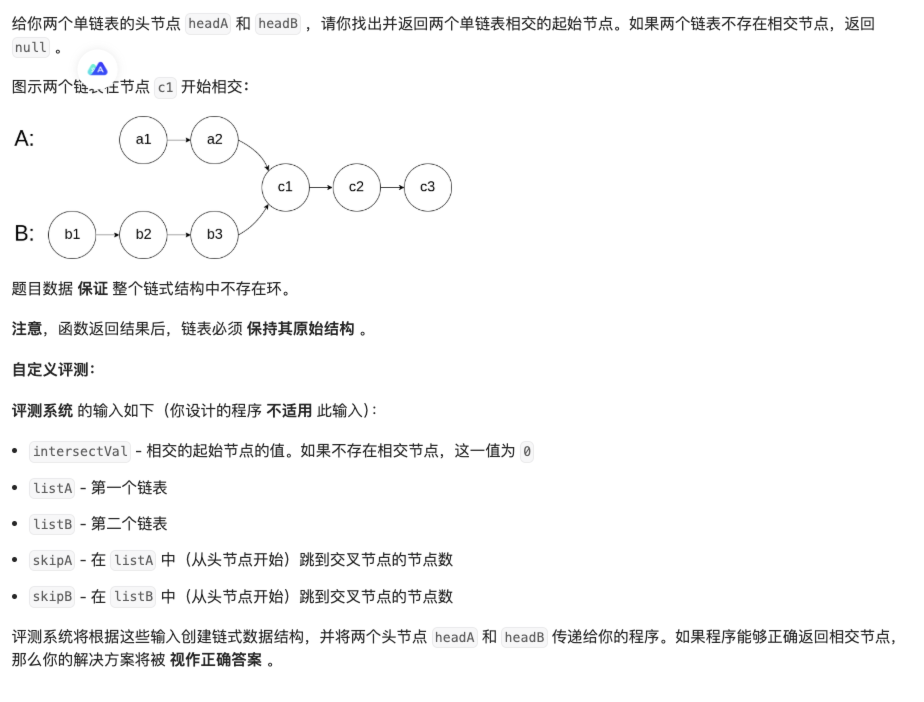
你看到题目，其实就是判断是否有两个元素相同，暴力法，对于链表A中的每一个节点，遍历链表B的所有节点，检查是否有节点地址相同的。

时间复杂度: O(L_A * L_B)

空间复杂度: O(1)

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 * int val;
 * ListNode *next;
 * ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        // 暴力法
        // 先判断边界情况
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }

        // 固定，遍历
        // 初始节点
        ListNode *ptA = headA;
        //flag 标志是否找到
        while (ptA != nullptr) {
            ListNode *ptB = headB;
            while (ptB != nullptr) {
                if (ptB == ptA) {
                    return ptB;
                }
                ptB = ptB->next;
            }
            ptA = ptA->next;
        }
        return nullptr;
    }
};

哈希集合法

其实很多判断两者是否相等的，都可以使用hash集合，因为hash的特点就是取值时间复杂度为O(1). 我们可以先遍历A链表，把这个链表的所有节点的地址存储到hash中，然后再遍历链表B,依次判断是否有节点地址和A中的相同。

时间复杂度: O(L_A + L_B)

空间复杂度: O(L_A) # 因为存储了hash

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 * int val;
 * ListNode *next;
 * ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        // 哈希集合法 find, count, insert 时间复杂度为O(1)
        // 先判断边界情况
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }

        // 定义集合
        unordered_set<ListNode*> nodeset;

        // 遍历链表A
        ListNode *ptA = headA;
        while (ptA != nullptr) {
            if (nodeset.find(ptA) == nodeset.end()) {
                nodeset.insert(ptA);
                ptA = ptA -> next;
            }
        }

        // 遍历链表B
        ListNode *ptB = headB;
        while (ptB != nullptr) {
            if (nodeset.find(ptB) != nodeset.end()) {
                return ptB;
            }
            ptB = ptB->next;
        }
        return nullptr;

        
    }
};

倒序法

因为如果两个链表相交了，那么他们在链表的末端肯定也是重叠的，那么其实我只要判断最后一个节点是否相等就知道是否相交了，但是也需要找到相交的起点，如果可以倒着遍历就解决了（换一个想法，我可以正向遍历的时候，用vector分别把A,B链表的节点地址存储下来，然后倒着对齐遍历这两个vector，一旦开始不相等，那么前一个地址就是相交点）

时间复杂度: O(LA+LB)

空间复杂度: O(LA+LB)

长度差法

这个方法其实和倒序法基本一样，也是考虑末端是重叠的，那么我只要计算出两个链表的长度，然后将长链表的起点前移，使得两个链表的剩余长度相等，最后再同步遍历寻找交点。

时间复杂度: O(LA+LB)

空间复杂度: O(1)

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 * int val;
 * ListNode *next;
 * ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        // 长度差法
        // 先判断边界情况
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        // 遍历A
        ListNode *ptA = headA;
        ListNode *ptB = headB;
        int length_A = 0;
        int length_B = 0;
        while (ptA != nullptr) {
            length_A = length_A + 1;
            ptA = ptA -> next;
        }
        while (ptB != nullptr) {
            length_B = length_B + 1;
            ptB = ptB -> next;
        }
        int diff = length_A - length_B;
        ListNode *longer = headA;
        ListNode *shorter = headB;

        if (length_A < length_B) {
            longer = headB;
            shorter = headA;
            diff = -1 * diff;
        }
        // 让长的先走
        for (int i = 0; i < diff; i++) {
            longer = longer->next;
        }
        while(longer != nullptr) {
            if (longer == shorter) {
                return longer;
            }
            longer = longer->next;
            shorter = shorter->next;
        }
        return nullptr;

        
        
    }
};

方法：双指针法

由于相交，那么当A链表走完之后还走B链表，B链表走完之后还走A链表的话，并且他们同时出发，那么如果有交点，那么肯定在交点出相遇

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 * int val;
 * ListNode *next;
 * ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        // 长度差法
        // 先判断边界情况
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *ptA = headA;
        ListNode *ptB = headB;

        while (ptA != ptB) {
            ptA = (ptA == nullptr) ? headB : ptA->next;

            ptB = (ptB == nullptr) ? headA : ptB->next;

        }
        return ptA; // 因为遍历完成后，要么就是要的交点，要么就是nullptr.
        
        
    }
};