🛸个人主页: dragoooon34
🚁所属专栏: C++
🚀操作环境: Visual Studio 2022

目录
[1-1 🍕AVL树的定义](#1-1 🍕AVL树的定义)
[2-1 🍔抽象图](#2-1 🍔抽象图)
[2-2 🍟插入流程](#2-2 🍟插入流程)
[2-3 🌭左单旋](#2-3 🌭左单旋)
[2-4 🍿右单旋](#2-4 🍿右单旋)
[2-5 🧂右左双旋](#2-5 🧂右左双旋)
[2-6 🥓左右双旋](#2-6 🥓左右双旋)
[2-7 🥚注意事项及调试技巧](#2-7 🥚注意事项及调试技巧)
[3-1 🍳检验依据](#3-1 🍳检验依据)
[3-2 🧇检验方法](#3-2 🧇检验方法)
[3-3 🥞AVL树的性能](#3-3 🥞AVL树的性能)
🌞前言
普通的二叉搜索树可能会退化为单支树(歪脖子树),导致搜索性能严重下降,为了解决这个问题,诞生了平衡二叉搜索树,主要是通过某些规则判断后,降低二叉树的高度,从而避免退化,本文介绍的 AVL 树就属于其中一种比较经典的平衡二叉搜索树,它是通过 平衡因子 的方式来降低二叉树高度的,具体怎么操作,可以接着往下看
🌜正文
一、😀认识AVL树
AVL 树由 前苏联 的两位数学家:G.M.Adelson-Velskii 和 E.M.Landis 共同提出,首次出现在 1962 发布的论文 《An algorithm for the organization of information》 中
具体实现原理为:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度
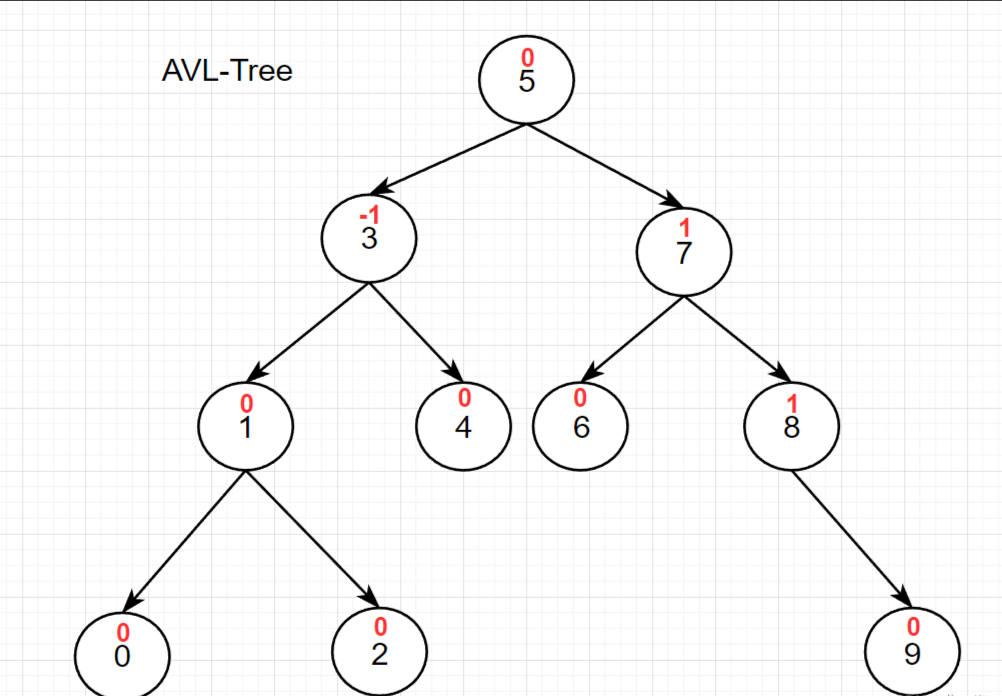
这两位天才提出的 二叉搜索树 解决方案十分巧妙,通过一个 平衡因子 bf 反映每一个节点中左右子树的高度情况,如果其中一方高度过高时(失衡,可能退化),就会通过 旋转 的方式降低高度,有效的避免了退化
如果 二叉搜索树 中节点具备以下性质
- 它的左右子树都是 AVL 树
- 左右子树的高度之差(平衡因子)的绝对值不超过 1
那么它就是一棵 AVL 树
注意: AVL 树是一棵高度平衡的二叉搜索树,如果它有 N 个节点,那么它的高度可以保持在 logN 左右,时间复杂度为 O(logN)
1-1 🍕AVL树的定义
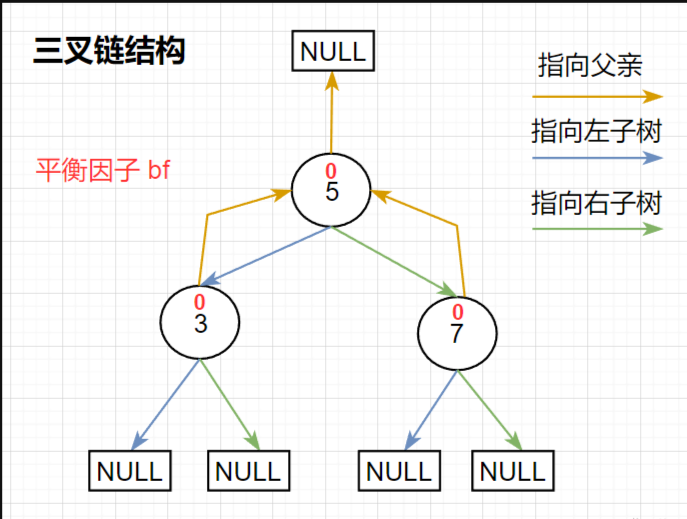
AVL 树在原 二叉搜索树 的基础上添加了 平衡因子 bf 以及用于快速向上调整的 父亲指针 parent ,所以
AVL树是一个三叉链结构所以 AVL 树的节点通过代码定义如下:
cpp//AVL树的节点类(key / value 模型) template<class K, class V> struct AVLTreeNode { AVLTreeNode(const std::pair<K, V> kv) :_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_kv(kv) ,_bf(0) { } AVLTreeNode<K, V>* _left; AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent; std::pair<K, V> _kv; int _bf; //平衡因子,默认:右 - 左 };至于 AVLTree 类中,只需要创建一个 根节点 _root 即可
注意: 当前实现的平衡因子,规定差值为 右 - 左,因此如果右子树增高,_bf++,左子树增高 _bf--,具体操作将在后面体现
二、😁AVL树的插入操作
注:本文仅对 AVL 树的插入操作做详解
2-1 🍔抽象图
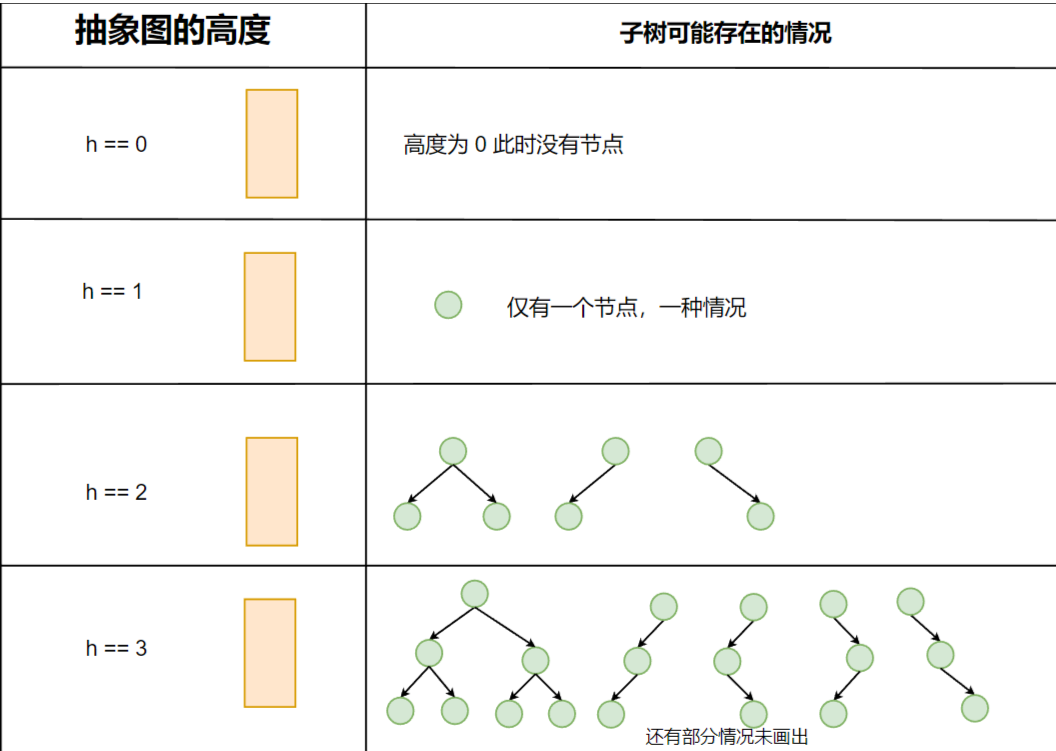
AVL 树的 旋转操作 比较复杂,需要考虑多种形状、多种情况,为了方便理解,将 部分节点 视为一个整体(抽象化),主要看高度
h进行旋转操作,可以得出下面这个抽象图抽象图很强大,通过 高度划分 ,可以 将所有的子树情况囊括其中
抽象图对于我们理解旋转过程帮助很大
2-2 🍟插入流程
AVL 树的插入流程与 二叉搜索树 一致,都是先找到合适位置,然后进行插入、链接,不过 AVL 树在链接之后,需要对 平衡因子 进行更新,并判断是否需要进行 旋转 以调整高度
插入流程:
- 判断根是否为空,如果为空,则进行第一次插入,成功后返回 true
- 找到合适的位置进行插入,如果待插入的值比当前节点值大,则往 右 路走,如果比当前节点值小,则往 左 路走
- 判断父节点与新节点的大小关系,根据情况判断链接至 左边 还是 右边
- 更新平衡因子,然后判断是否需要进行 旋转 调整高度
代码片段如下(不包括判断 旋转 部分的具体实现)
cpp//插入节点 bool Insert(const std::pair<K, V> kv) { if (_root == nullptr) { _root = new Node(kv); return true; } //易错点:没有提前记录父亲 Node* parent = nullptr; Node* cur = _root; while (cur) { if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; } else if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; } else return false; } //创建新节点,链接 cur = new Node(kv); if (parent->_kv.first < kv.first) { parent->_right = cur; cur->_parent = parent; } else { parent->_left = cur; cur->_parent = parent; } //根据平衡因子判断是否需要旋转 while (parent) { //更新平衡因子 if (parent->_right == cur) parent->_bf++; else parent->_bf--; //判断是否需要调整 //...... } return true; }注:
AVL树的插入返回值也是 布尔类型根据平衡因子判断是否需要旋转这一部分非常重要,共有四种不同的旋转方式,下面将会逐个讲解,配合动图,逐个击破
2-3 🌭左单旋
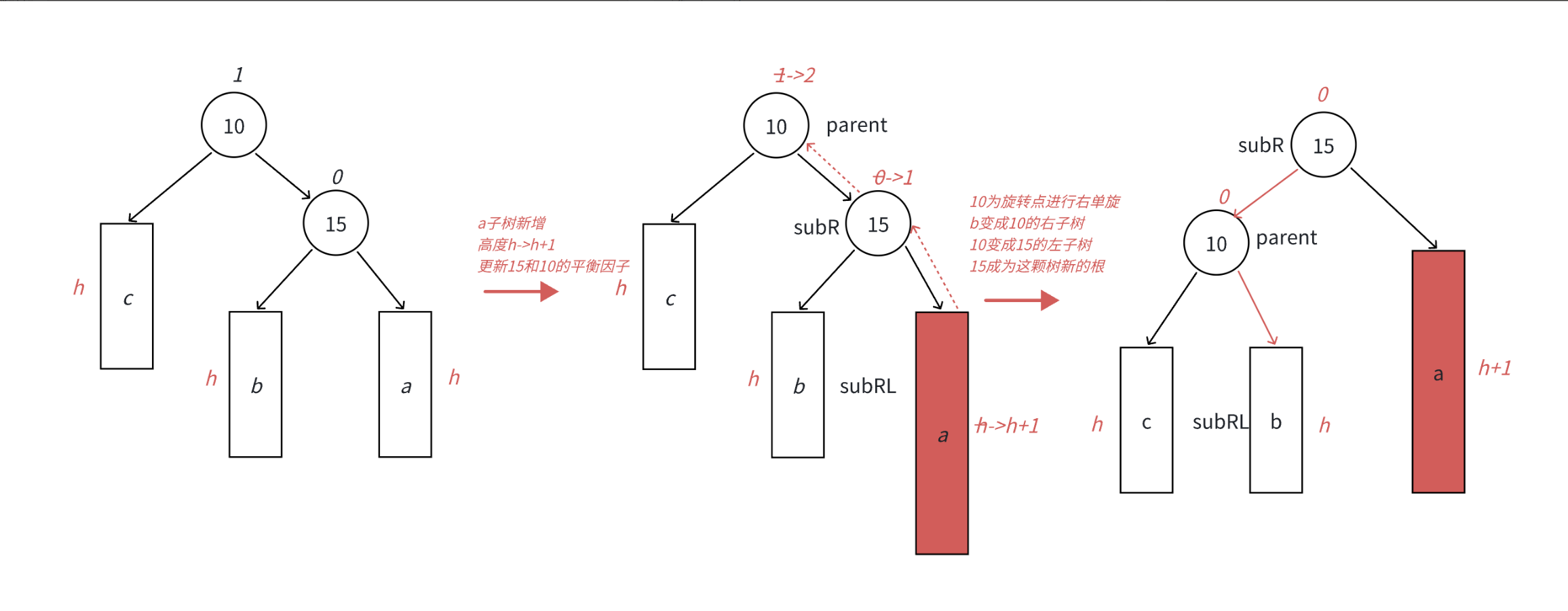
• 本图展⽰的是10为根的树,有a/b/c抽象为三棵⾼度为h的⼦树(h>=0),a/b/c均符合AVL树的要求。10可能是整棵树的根,也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树, 是⼀种概括抽象表⽰,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体跟上⾯左旋类似。
• 在a⼦树中插⼊⼀个新结点,导致a⼦树的⾼度从h变成h+1,不断向上更新平衡因⼦,导致10的平衡因⼦从1变成2,10为根的树左右⾼度差超过1,违反平衡规则。10为根的树右边太⾼了,需要往左边旋转,控制两棵树的平衡。
• 旋转核⼼步骤,因为10 < b⼦树的值 < 15,将b变成10的右⼦树,10变成15的左⼦树,15变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的⾼度恢复到了插⼊之前的h+2,符合旋转 原则。如果插⼊之前10整棵树的⼀个局部⼦树,旋转后不会再影响上⼀层,插⼊结束了。
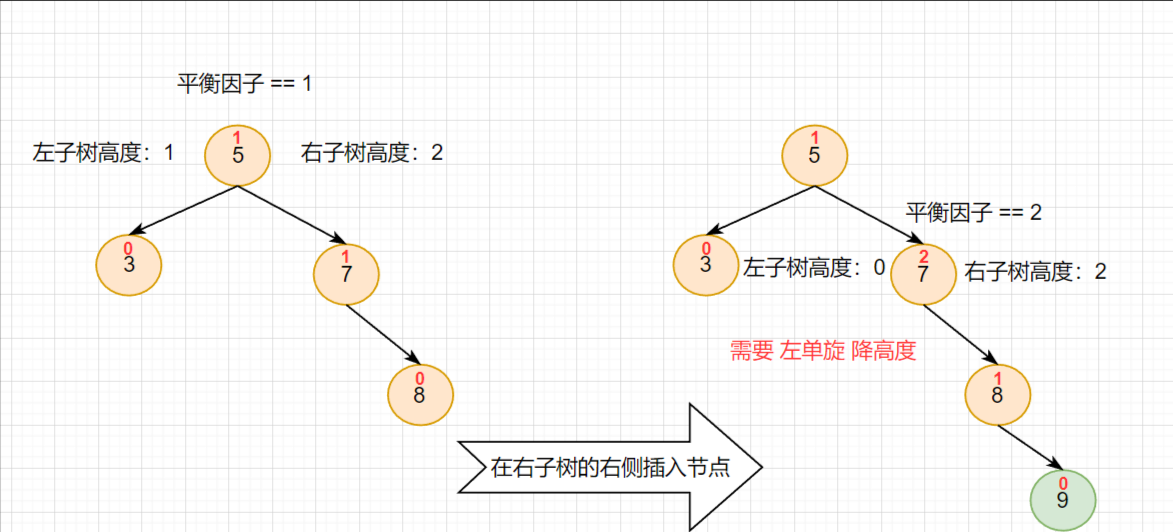
左单旋的适用场景如下:在根的右子树中出现 平衡因子 为 1 的情况下,仍然往右侧插入节点,插入后会导致 右子树 中某个节点 平衡因子 值为 2 ,此时就需要使用 左单旋 降低高度
显然,当节点 9 插入后,节点 7 的 平衡因子 变成了 2:表示它的左右子树高度差大于 1
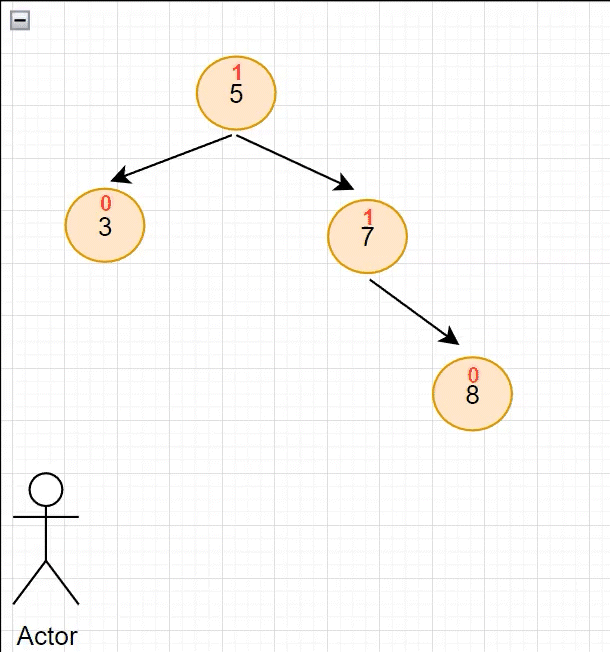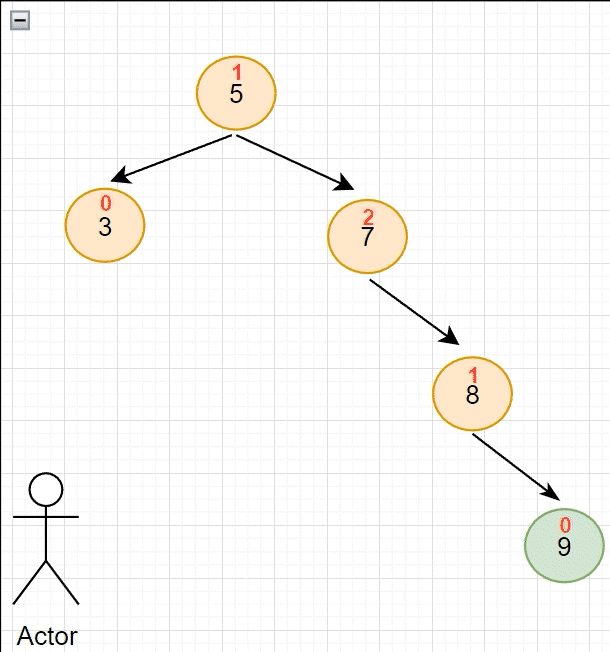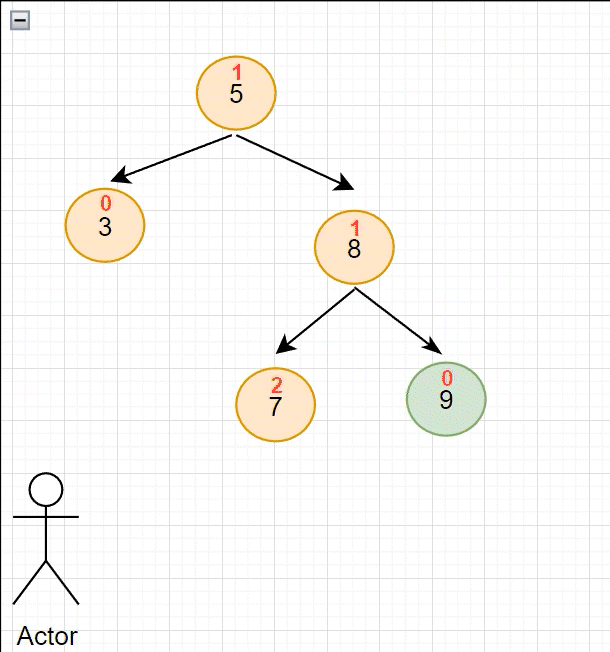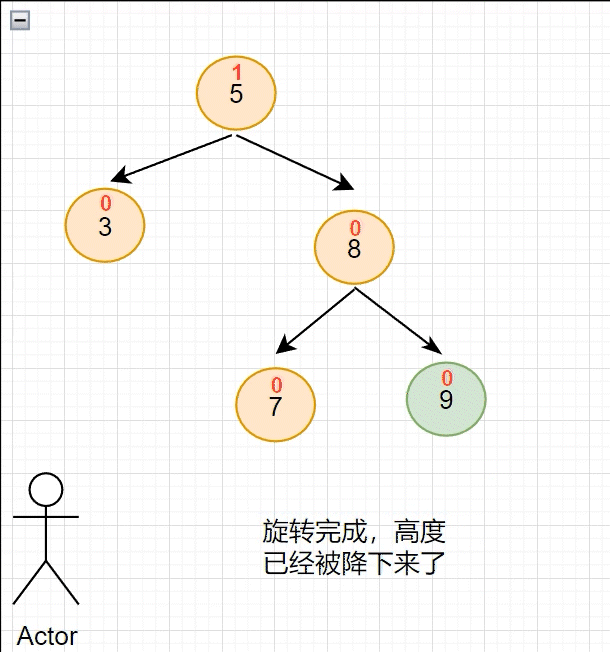
既然节点 7 出了问题,那就要对他进行旋转;因为现在插入的节点位于 右子树的右侧 ,所以需要 左单旋
具体代码实现如下:
cpp//左单旋 void RotateL(Node* parent) { Node* subR = parent->_right; Node* subRL = subR->_left; //先将 subR 的左孩子移交给父亲 parent->_right = subRL; if (subRL != nullptr) subRL->_parent = parent; Node* pparent = parent->_parent; //易错点:忘记更改原父亲的链接关系 subR->_left = parent; parent->_parent = subR; //易错点:判断 等于 写成 赋值 //再将父亲移交给 subR,subR 成为新父亲 if (parent == _root) { //如果原父亲为根,那么此时需要更新 根 subR->_parent = nullptr; _root = subR; } else { //单纯改变链接关系 if (pparent->_right == parent) pparent->_right = subR; else pparent->_left = subR; subR->_parent = pparent; } //更新平衡因子 parent->_bf = subR->_bf = 0; }旋转过程其实就是更改链接的过程
因为是三叉链结构,所以需要注意 _parent 的调整
对于上面的用例,旋转过程如下图所示(动图)
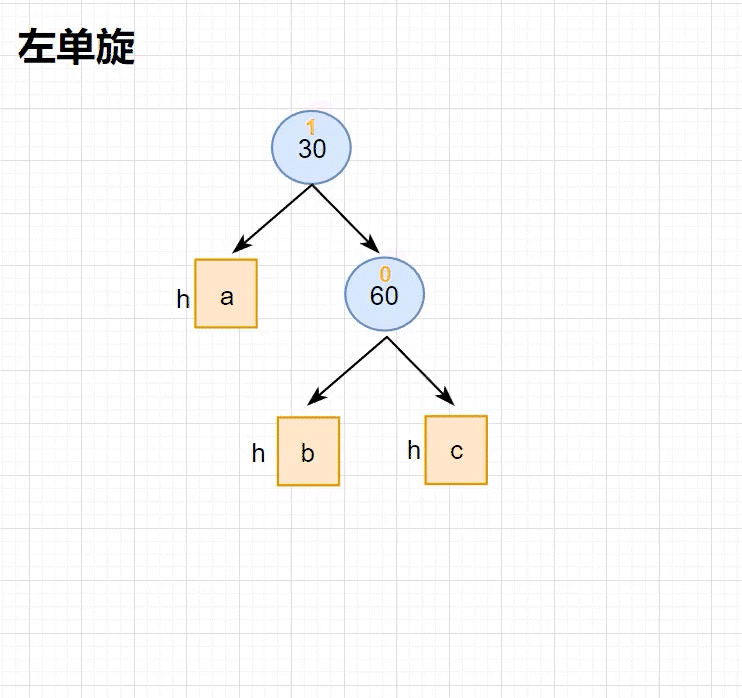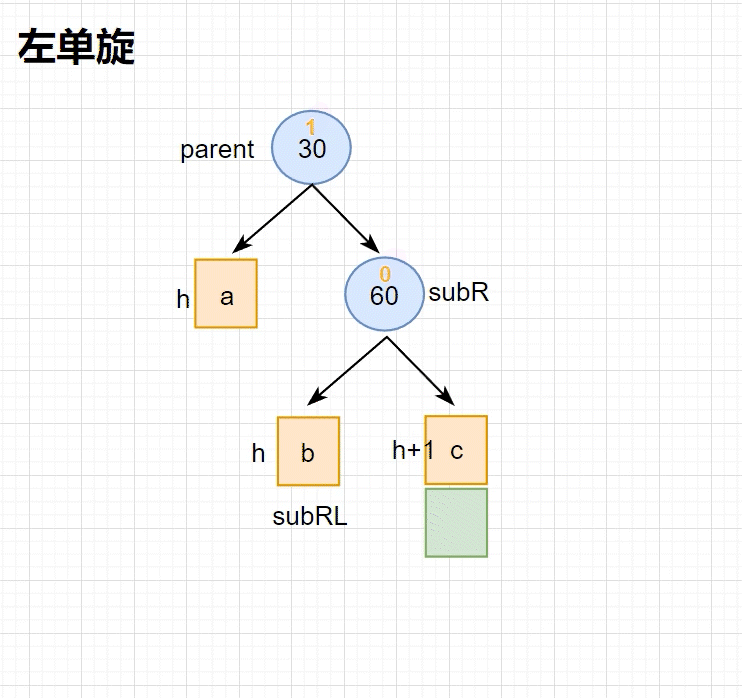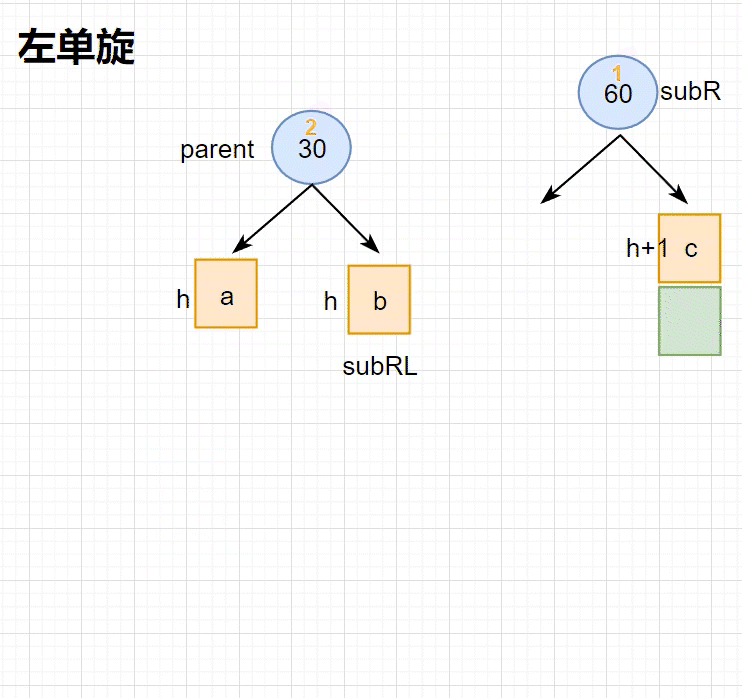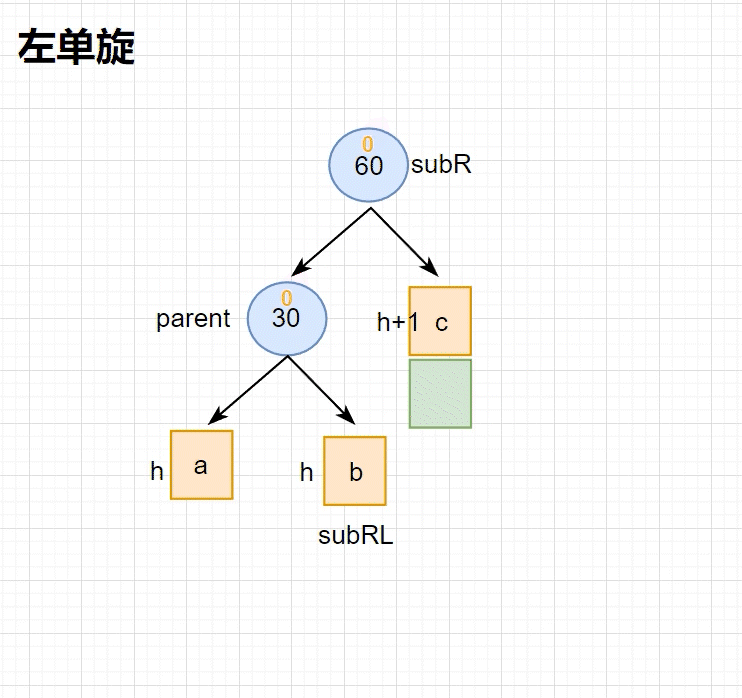
此时抽象图的高度为 1,将 子树 抽象化,可以得到下图中的 左单旋 过程(动图)
因为是 抽象图 ,所以其中的 黄色色块 可以变换成 任意高度的子树 ,无论如何变换,左单旋 的逻辑都不会发生改变
旋转逻辑:
- 确定 parent、subR、subRL
- 将 subRL 托付给 parent
- 令 parent 成为 subR 的左子树
- 需要特别注意父指针的更改以及根节点的更新
注意: subRL 可能是 nullptr,在改变其链接关系时,需要判断一下,避免空指针解引用行为;parent 可能是 根节点,subR 在链接后,需要更新 根节点;左单旋后,parent、subR 的平衡因子都可以更新为 0,此时是很平衡的
2-4 🍿右单旋
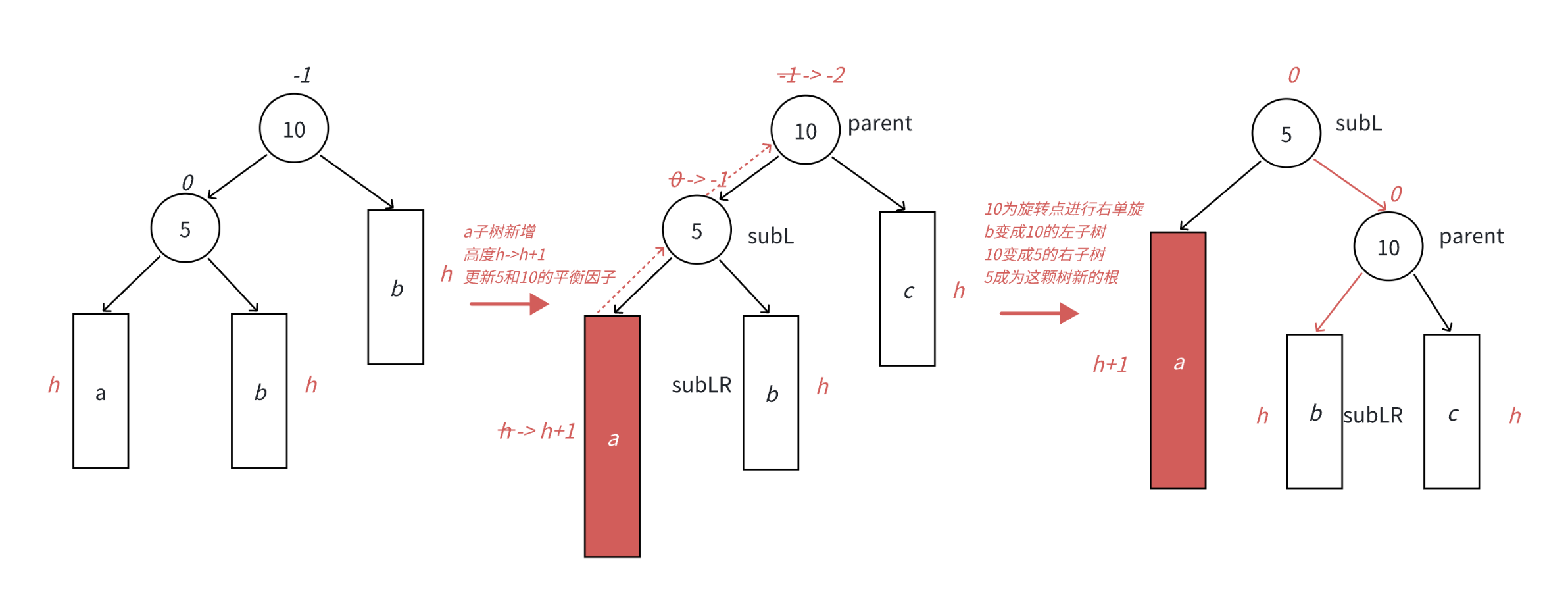
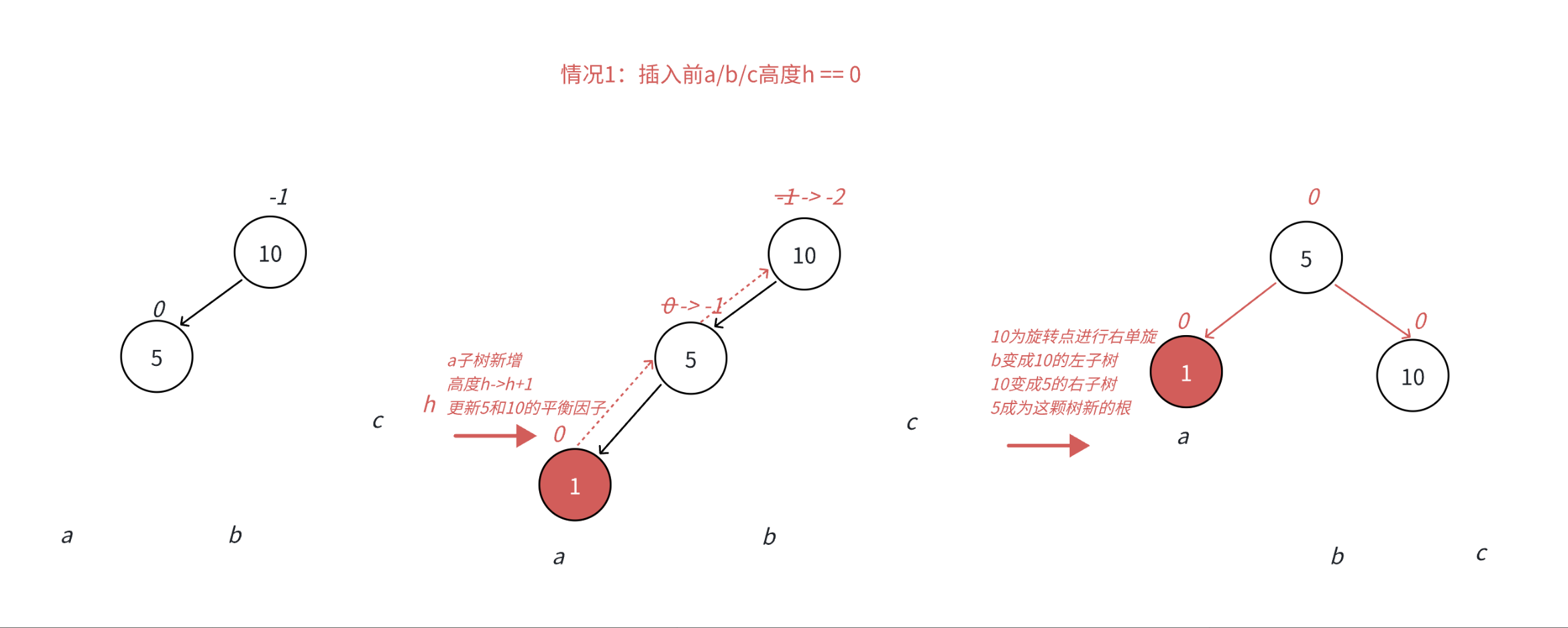
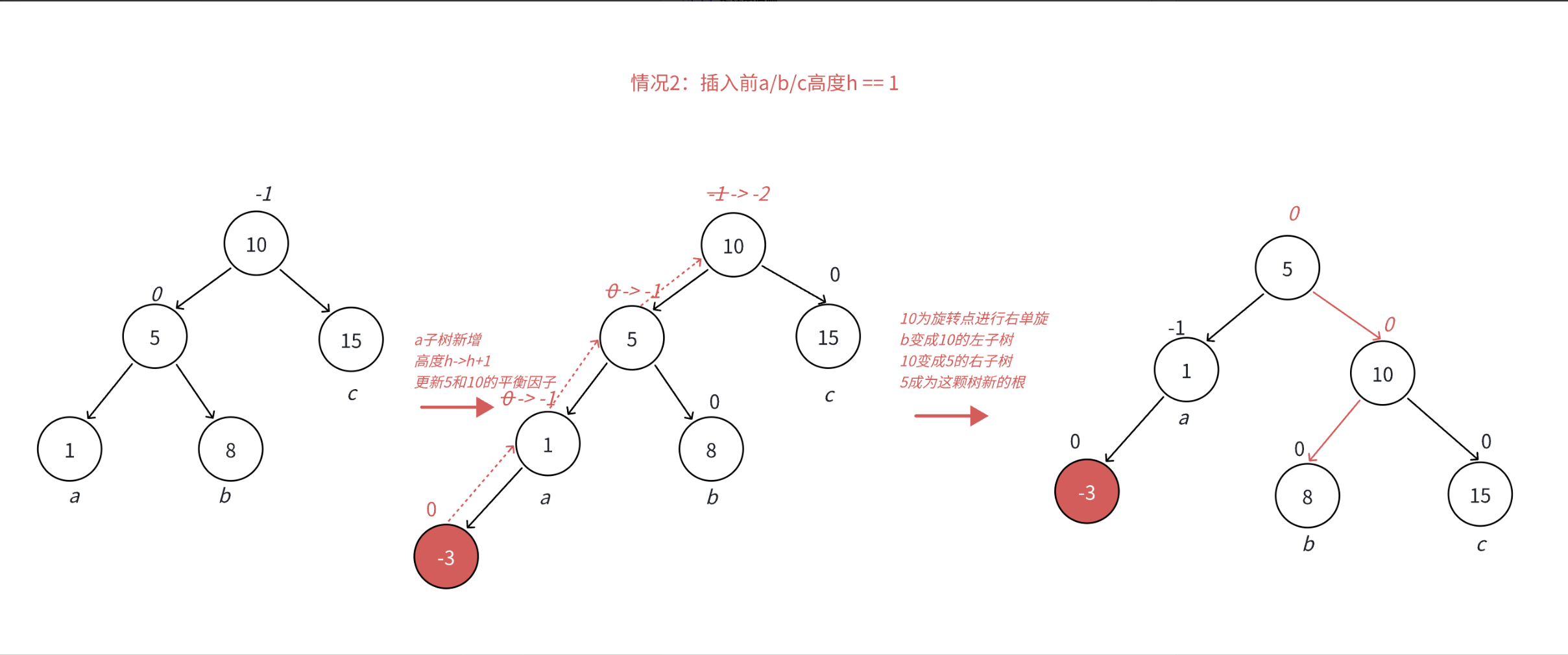
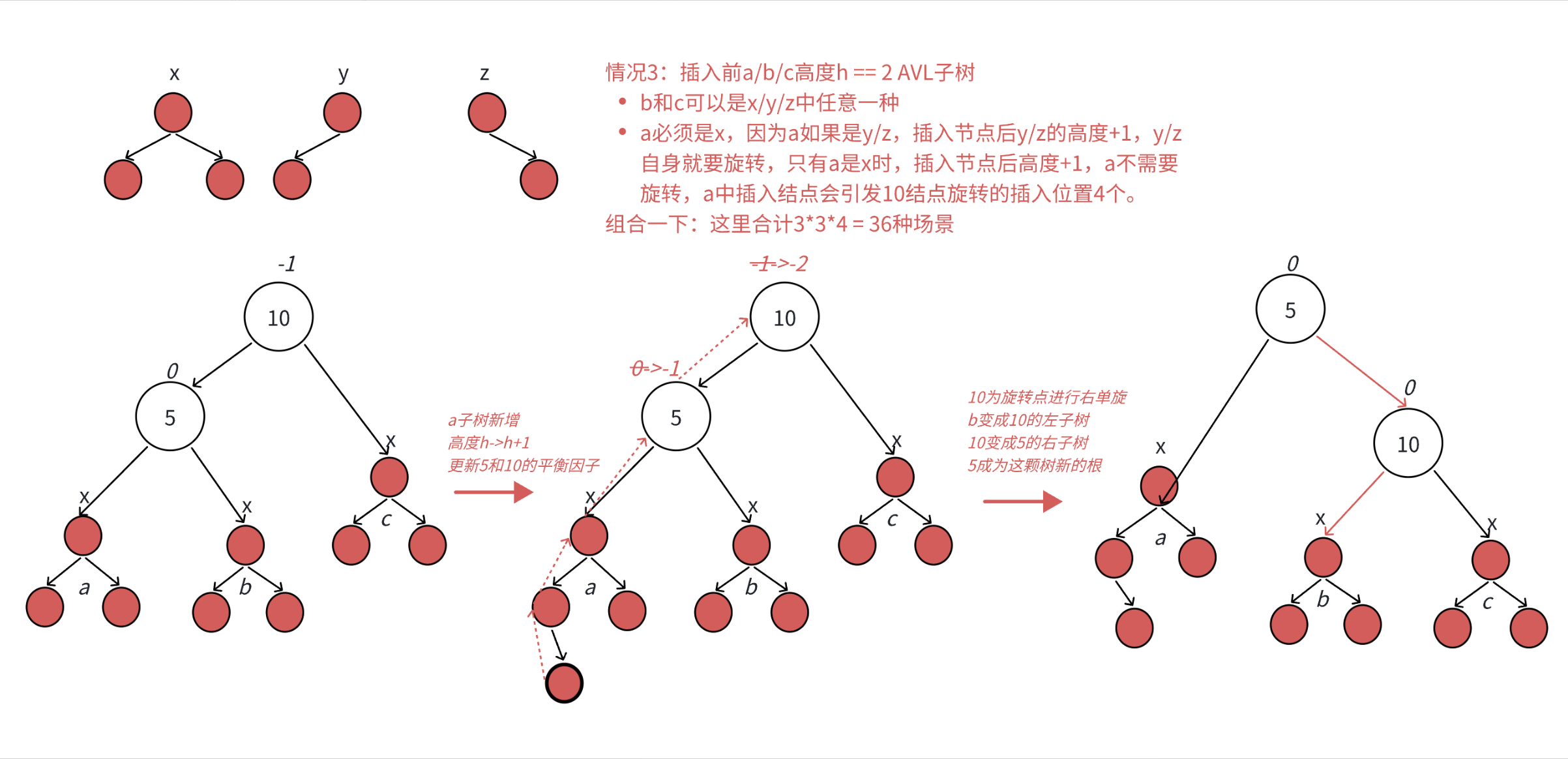
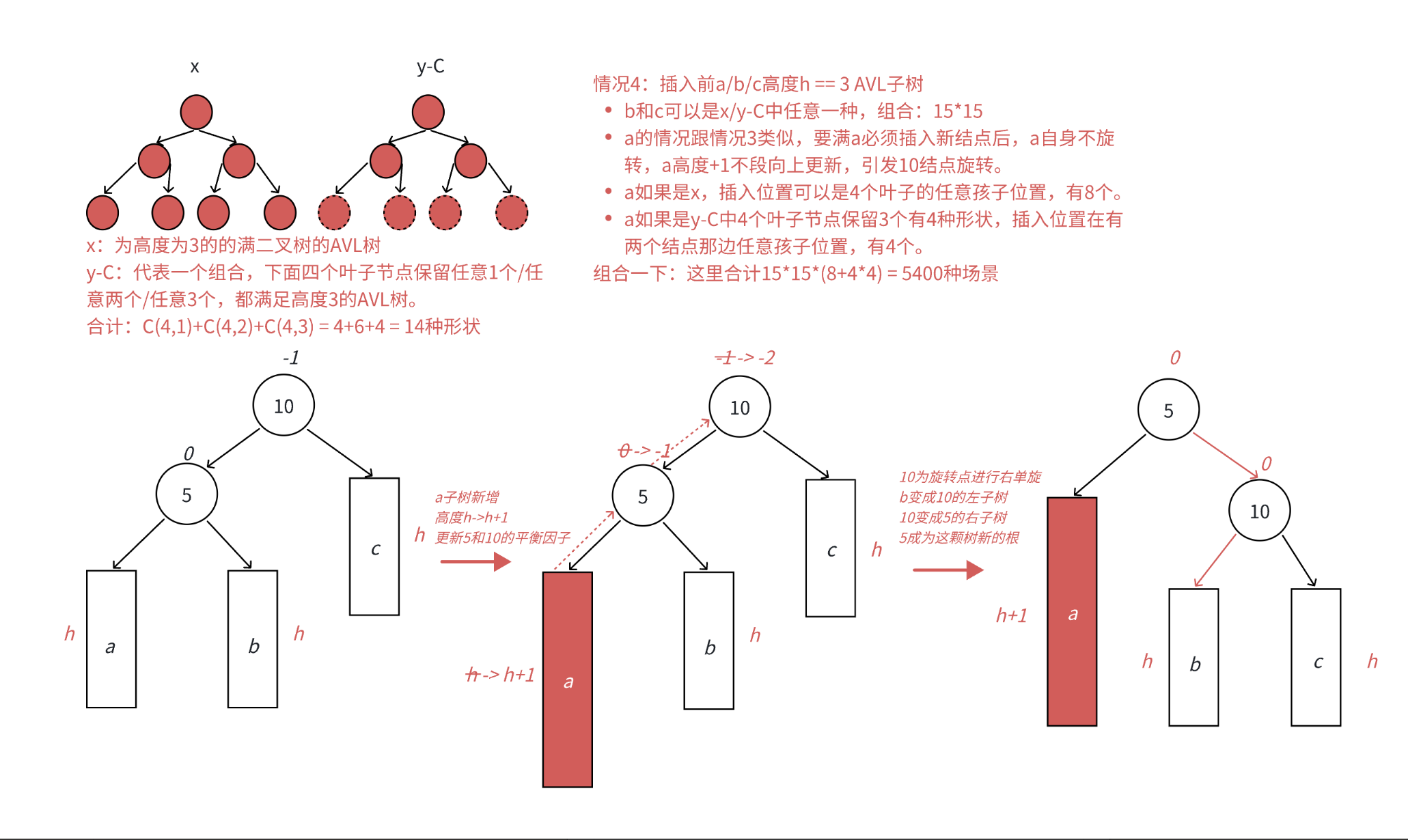
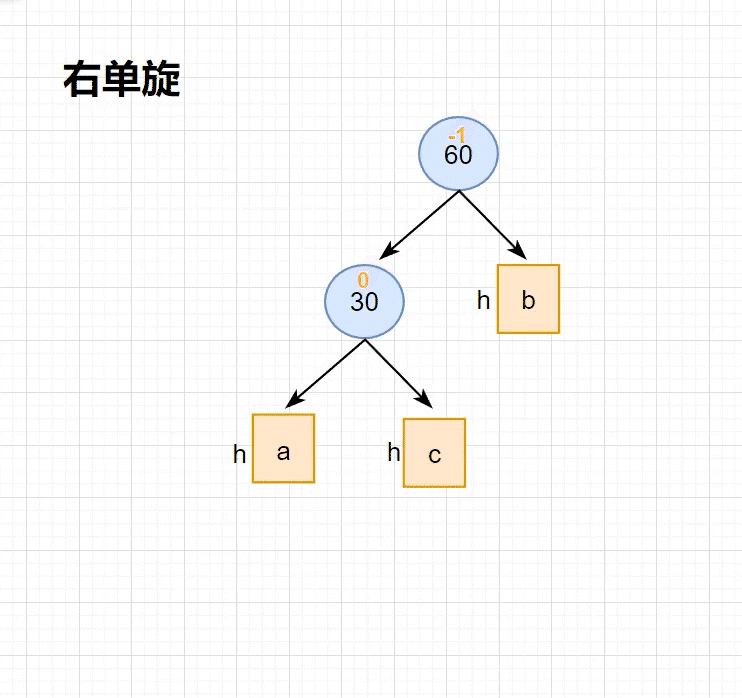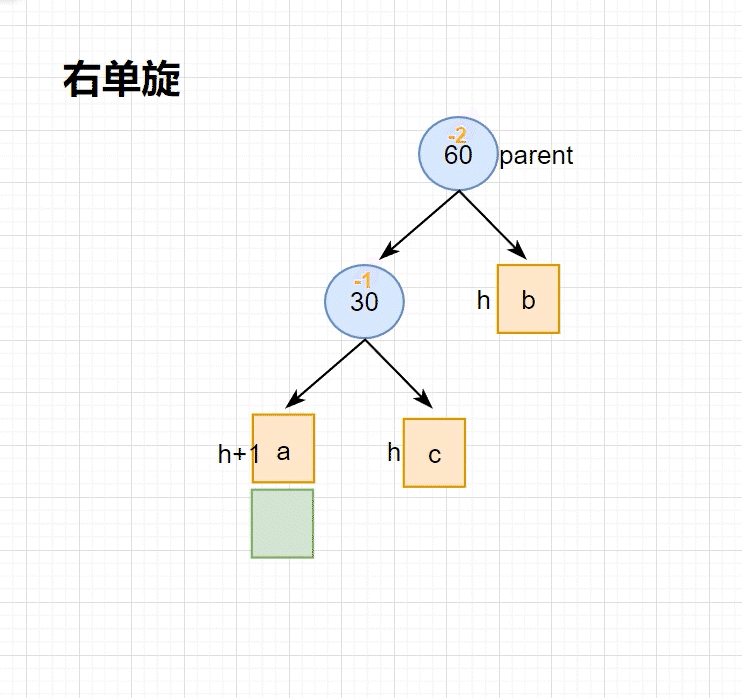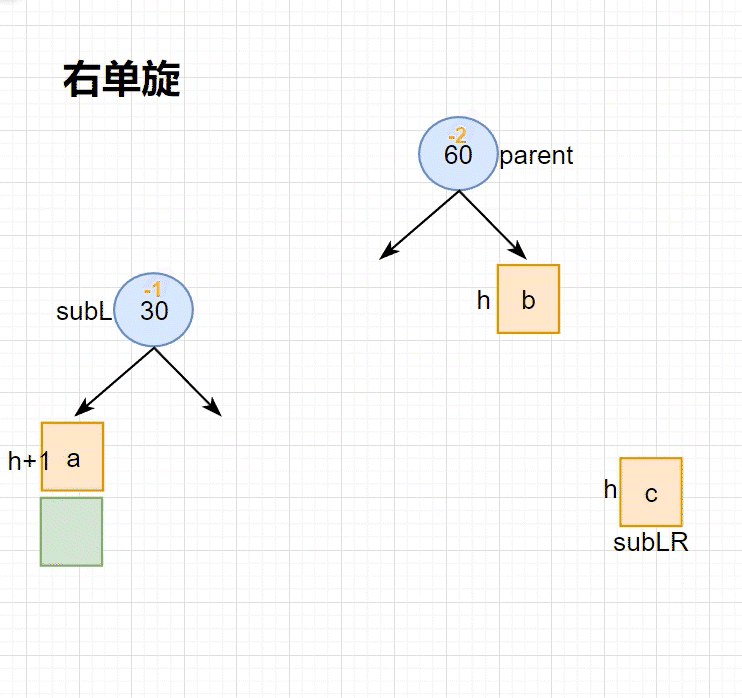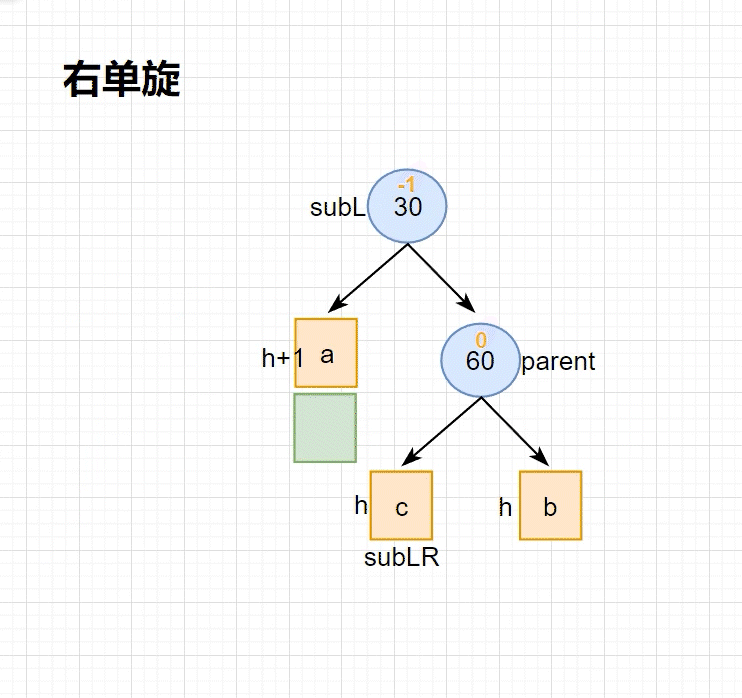
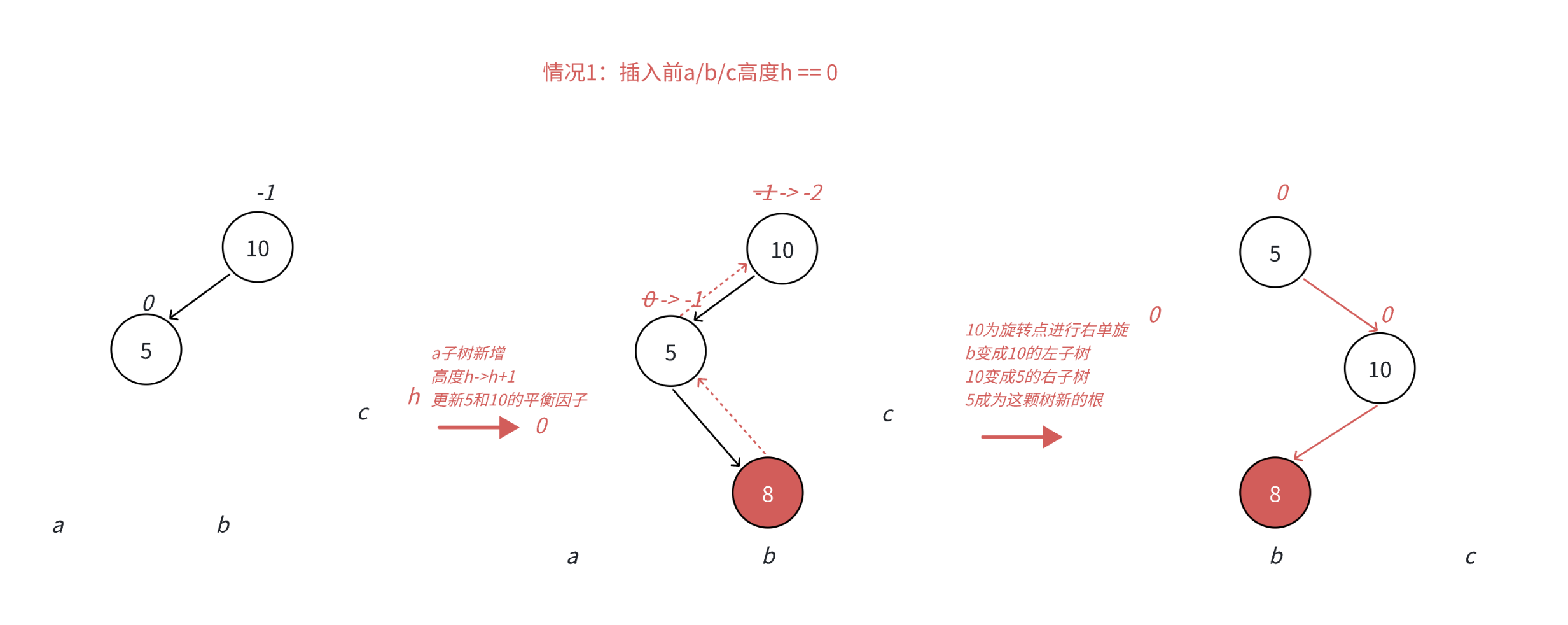
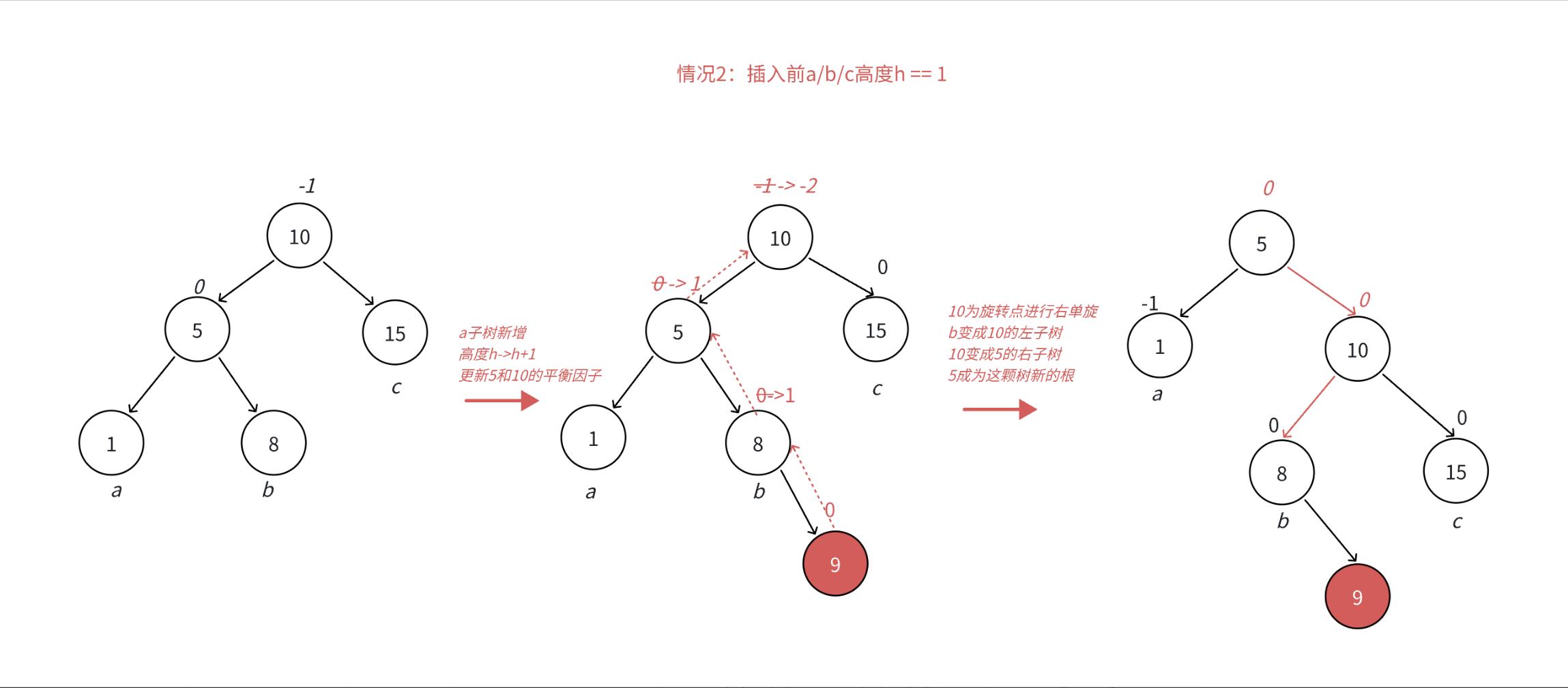
•本图展⽰的是10为根的树,有a/b/c抽象为三棵⾼度为h的⼦树(h>=0),a/b/c均符合AVL树的要求。10可能是整棵树的根,也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树,是⼀种概括抽象表⽰,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体图2/图3/图4/图5进⾏了详细描述。
•在a⼦树中插⼊⼀个新结点,导致a⼦树的⾼度从h变成h+1,不断向上更新平衡因⼦,导致10的平衡因⼦从-1变成-2,10为根的树左右⾼度差超过1,违反平衡规则。10为根的树左边太⾼了,需要往右边旋转,控制两棵树的平衡。
•旋转核⼼步骤,因为5 < b⼦树的值 < 10,将b变成10的左⼦树,10变成5的右⼦树,5变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的⾼度恢复到了插⼊之前的h+2,符合旋转原则。如果插⼊之前10整棵树的⼀个局部⼦树,旋转后不会再影响上⼀层,插⼊结束了。
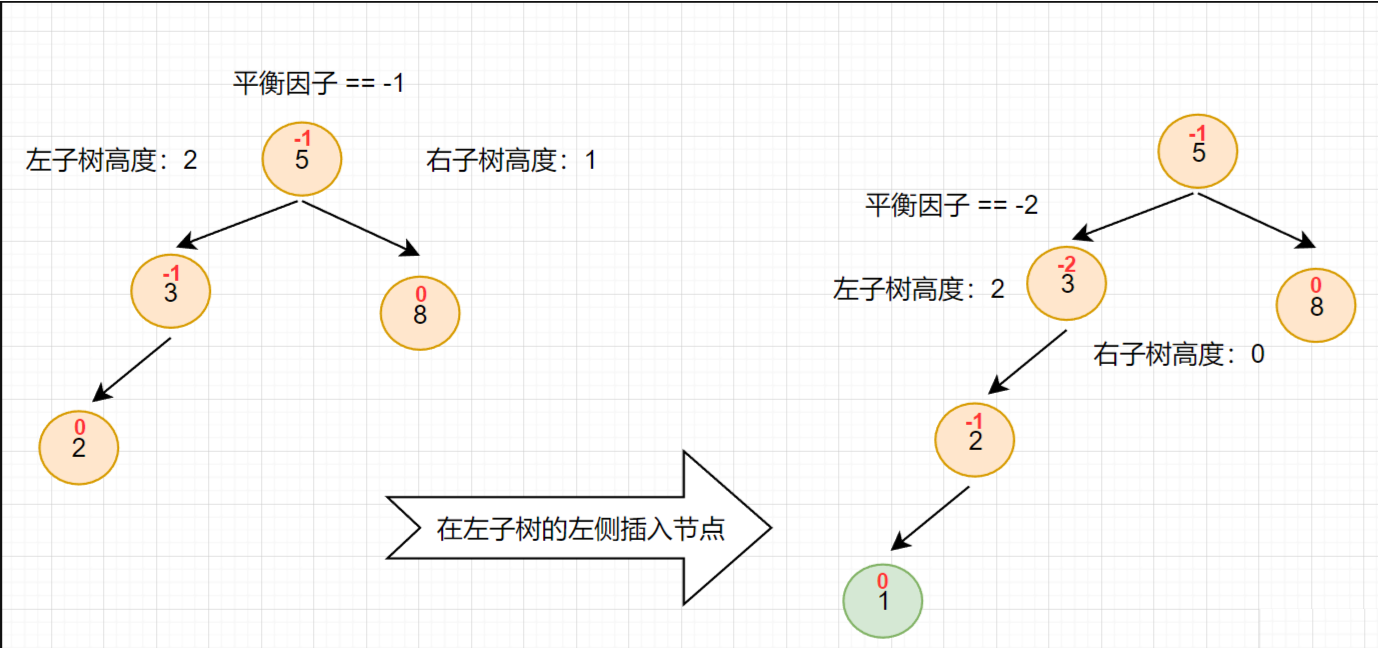
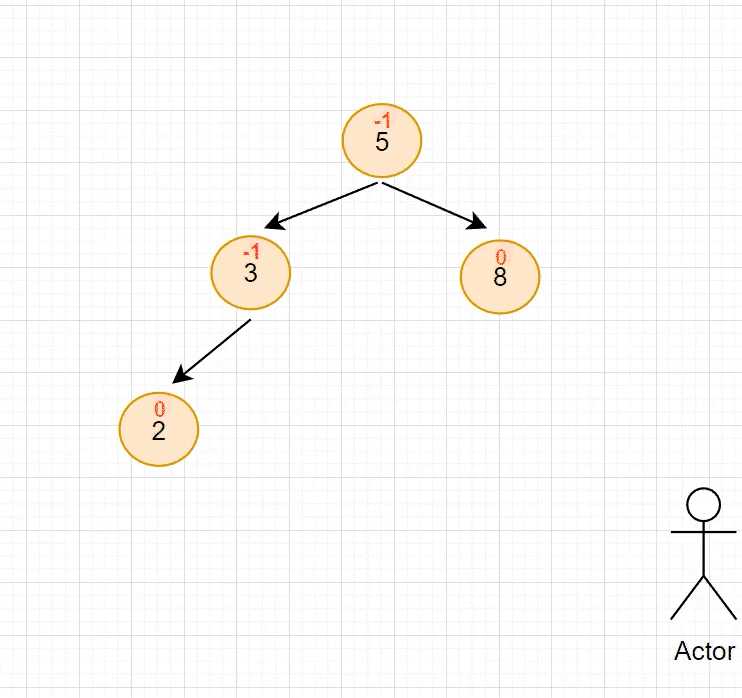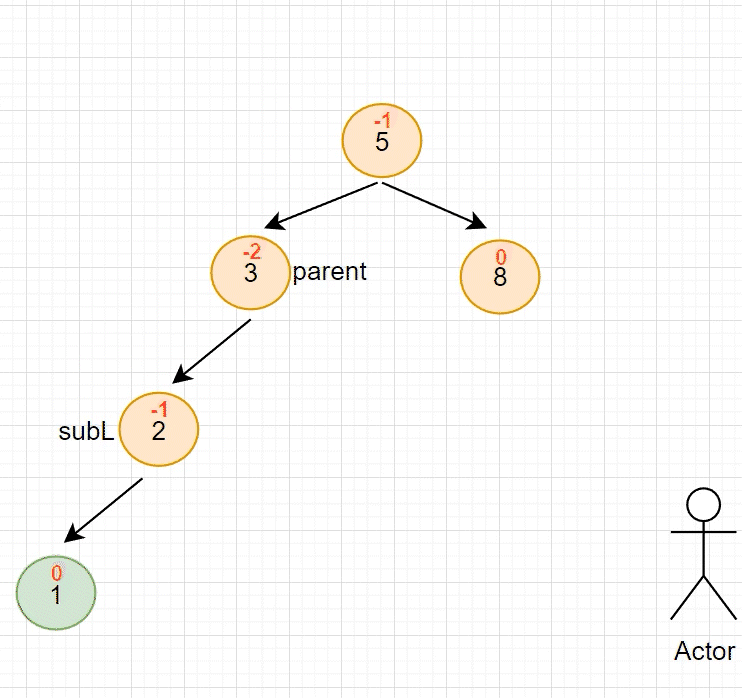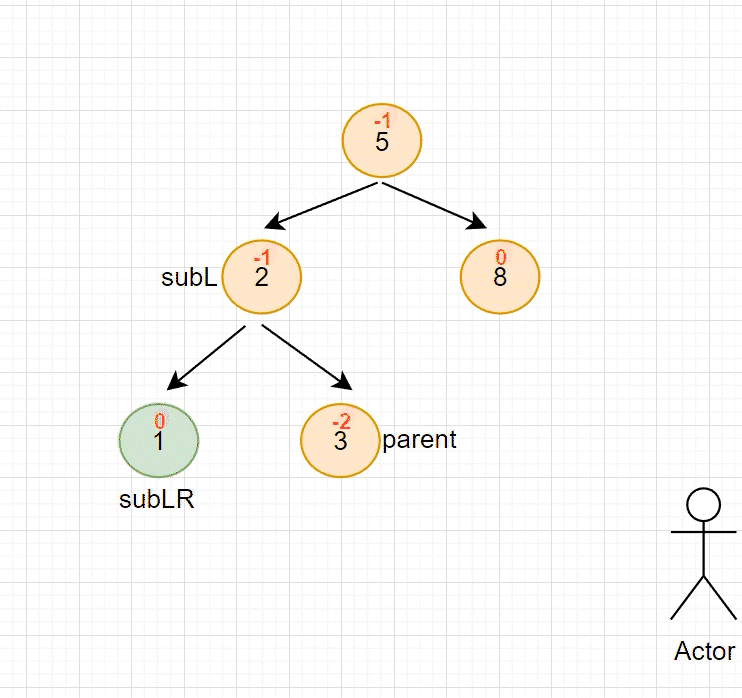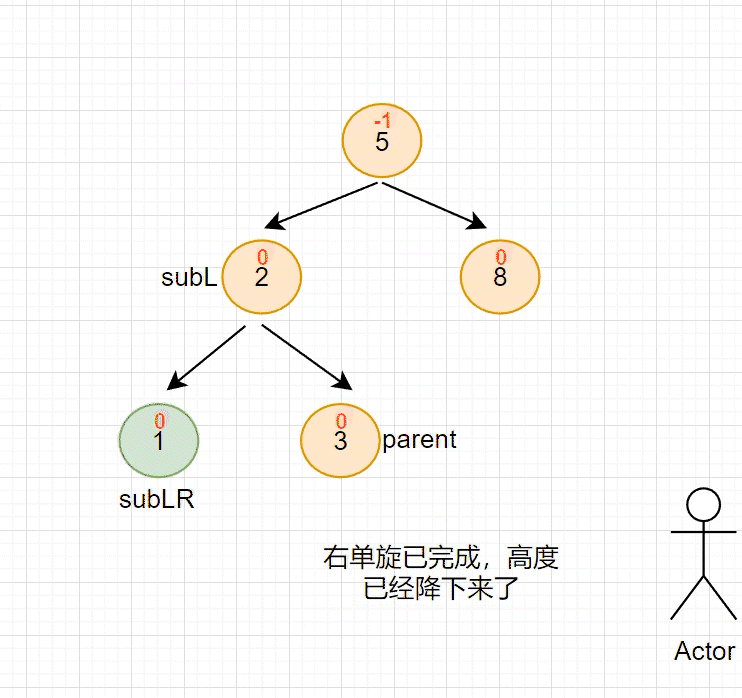
右单旋的适用场景如下:在根的左子树中出现 平衡因子 为 1 的情况下,仍然往左侧插入节点,插入后会导致 左子树 中某个节点 平衡因子 值为 2 ,此时就需要使用 右单旋 降低高度
右单旋 的场景与 左单旋 如出一辙,不过方向不同而已
当节点 1 插入后,节点 3 的左右子树高度差 > 1,此时插入的节点位于左子树的左侧,需要 右旋转 降低高度
右单旋 代码,与 左单旋 几乎一模一样
cpp//右单旋 void RotateR(Node* parent) { Node* subL = parent->_left; Node* subLR = subL->_right; //先将 subL 的右孩子移交给父亲 parent->_left = subLR; if (subLR != nullptr) subLR->_parent = parent; Node* pparent = parent->_parent; subL->_right = parent; parent->_parent = subL; //再将父亲移交给 subL,subL 成为新父亲 if (parent == _root) { //如果原父亲为根,那么此时需要更新 根 subL->_parent = nullptr; _root = subL; } else { //单纯改变链接关系 if (pparent->_right == parent) pparent->_right = subL; else pparent->_left = subL; subL->_parent = pparent; } //更新平衡因子 parent->_bf = subL->_bf = 0; }上面例子的旋转流程如下图所示(动图)
此时同样是 子树高度为 1 的情况 ,使用抽象图,右单旋 的旋转过程如下所示
右单旋 旋转逻辑:
- 确定 parent、subL、subLR
- 将 subLR 托付给 parent
- 令 parent 成为 subL 的右子树
- 需要特别注意父指针的更改以及根节点的更新
注意: subLR 可能是 nullptr,在改变其链接关系时,需要判断一下,避免空指针解引用行为;parent 可能是 根节点,subL 在链接后,需要更新 根节点;右单旋后,parent、subLR 的平衡因子都可以更新为 0,此时是很平衡的
2-5 🧂右左双旋
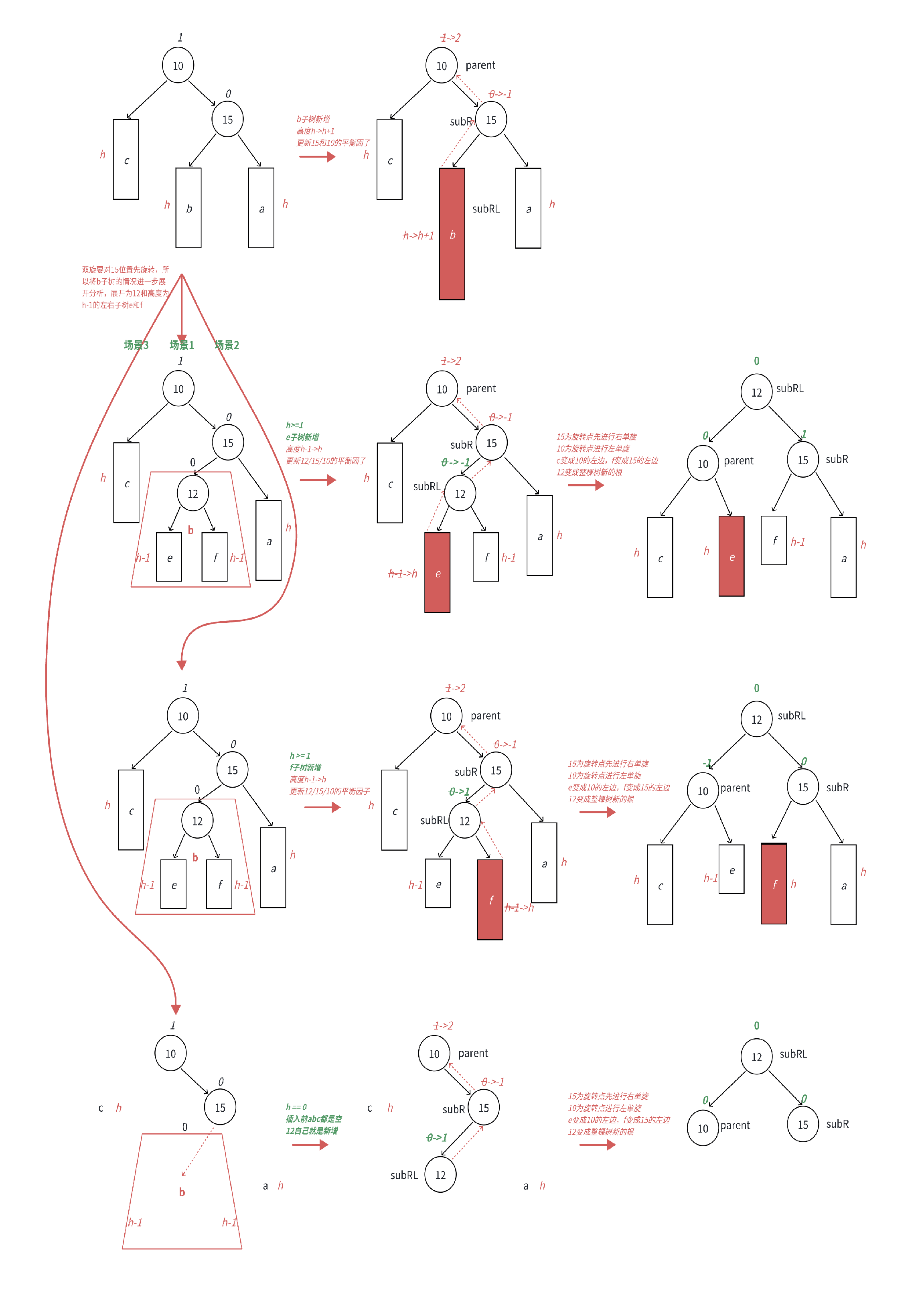
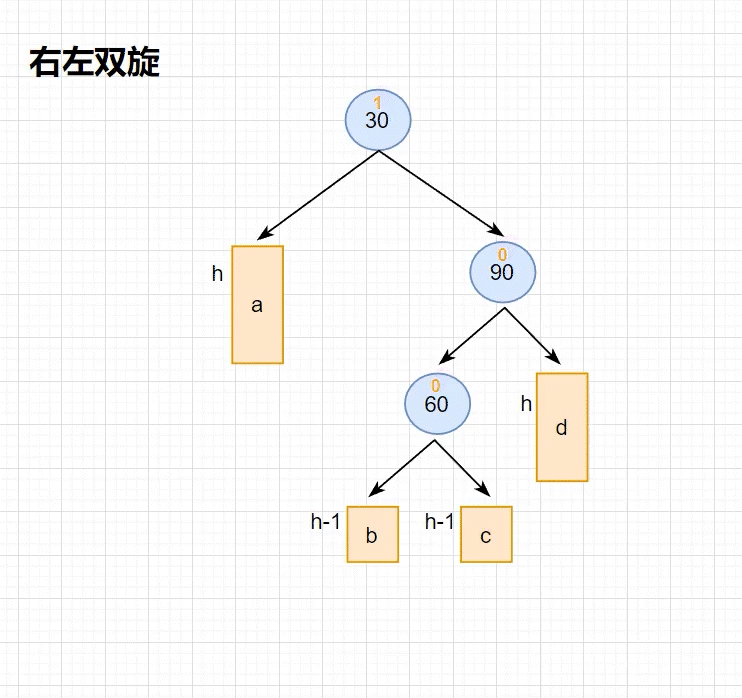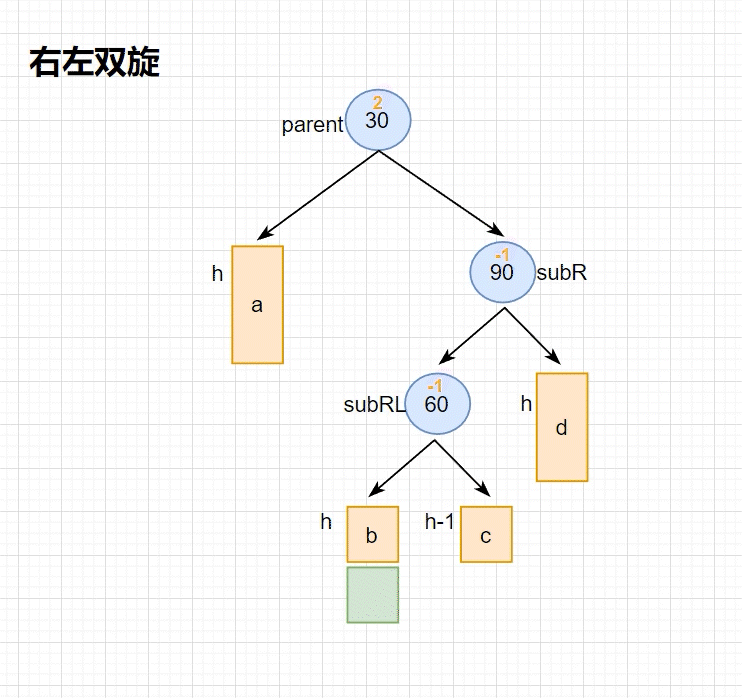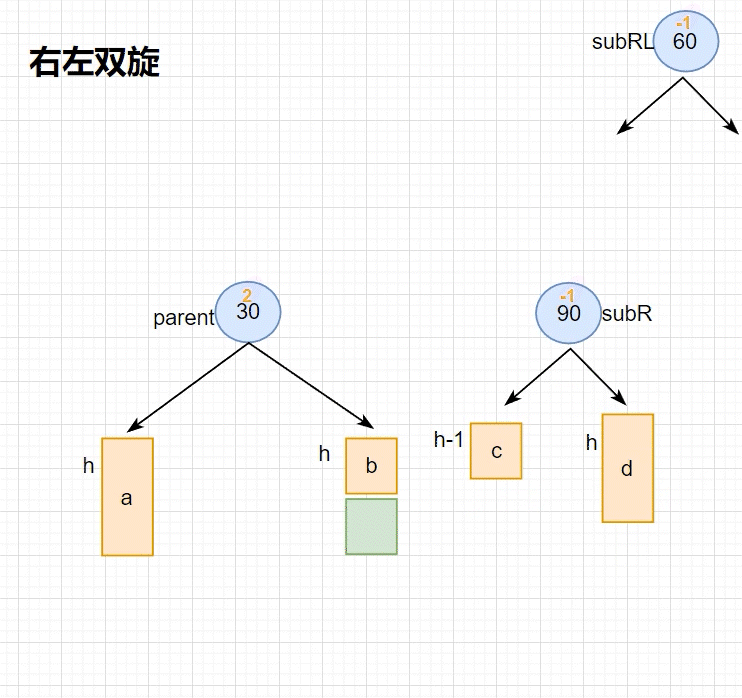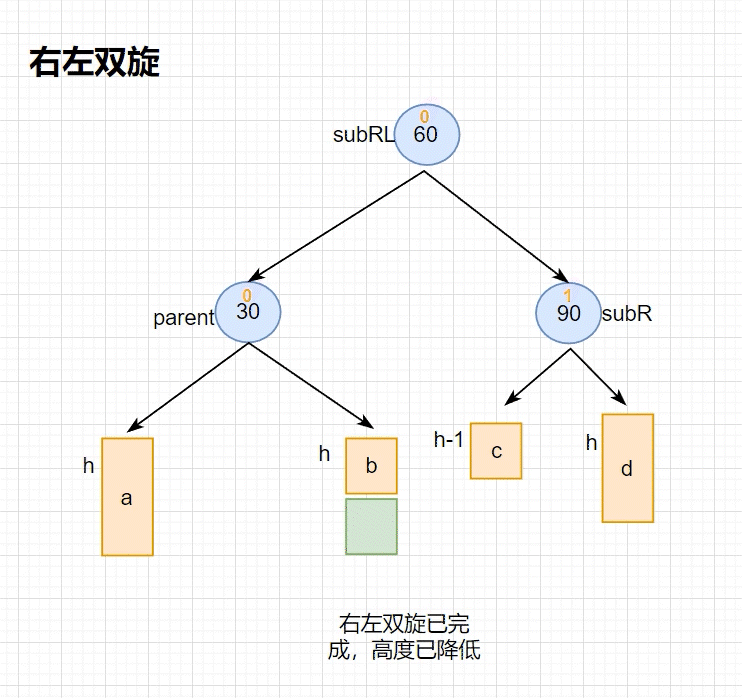
•跟左右双旋类似,下⾯我们将a/b/c⼦树抽象为⾼度h的AVL⼦树进⾏分析,另外我们需要把b⼦树的细节进⼀步展开为12和左⼦树⾼度为h-1的e和f⼦树,因为我们要对b的⽗亲15为旋转点进⾏右单旋,右单旋需要动b树中的右⼦树。b⼦树中新增结点的位置不同,平衡因⼦更新的细节也不同,通过观察12的平衡因⼦不同,这⾥我们要分三个场景讨论。
•场景1:h >= 1时,新增结点插⼊在e⼦树,e⼦树⾼度从h-1变为h并不断更新12->15->10平衡因⼦,引发旋转,其中12的平衡因⼦为-1,旋转后10和12平衡因⼦为0,15平衡因⼦为1。
•场景2:h >= 1时,新增结点插⼊在f⼦树,f⼦树⾼度从h-1变为h并不断更新12->15->10平衡因⼦,引发旋转,其中12的平衡因⼦为1,旋转后15和12平衡因⼦为0,10平衡因⼦为-1。
•场景3:h == 0时,a/b/c都是空树,b⾃⼰就是⼀个新增结点,不断更新15->10平衡因⼦,引发旋转,其中12的平衡因⼦为0,旋转后10和12和15平衡因⼦均为0。
当值插入 右子树的右侧 时,可能引发 左单旋 ,当值插入 左子树的左侧 时,则可能引发 右单旋
如果插入的是 右子树的左侧 或 左子树的右侧 时,则可能引发 双旋
比如 插入右子树的左侧 时,单单凭借 左单旋 无法解决问题,需要 先进行 右单旋,再进行 左单旋 才能 降低高度 ,这一过程就成为 双旋(右左双旋)
代码实现很简单,根据不同的位置调用 右单旋 和 左单旋 即可
cpp//右左双旋 void RotateRL(Node* parent) { Node* subR = parent->_right; Node* subRL = subR->_left; int BF = subRL->_bf; //先右单旋 RotateR(subR); //再左单旋 RotateL(parent); //根据不同的情况更新平衡因子 if(BF == 0) { parent->_bf = subR->_bf = 0; } else if (BF == 1) { parent->_bf = -1; subR->_bf = 0; subRL->_bf = 0; } else if (BF == -1) { parent->_bf = 0; subR->_bf = 1; subRL->_bf = 0; } else { //非法情况 std::cerr << "此处的平衡因子出现异常!" << std::endl; assert(false); //直接断言报错 } }右左双旋 的抽象图 旋转 流程如下(动图)
注:双旋 部分的动图省略了部分细节,着重展现 高度降低 的现象
右左双旋 逻辑:
- 确定 parent、subR、subRL
- 将 subRL 的右子树托付给 subR,左子树托付给 parent
- subRL 向上提,整体高度下降
- 需要特别注意平衡因子的调整
双旋 的 平衡因子 调整需要分类讨论:
情况一 :新节点插入至右子树左侧后,subRL 平衡因子变为 0,此时树变得更加平衡了,因此 parent、subR、subRL 三者的平衡因子都为 0情况二:新节点插入至右子树的左侧后,subRL 平衡因子变为 -1,证明 新节点插入至 subRL 的左边,并且右边没有东西,旋转后,将新节点托付给 parent 后,parent 变得平衡了,但 subR 因没有分到节点,因此导致其左侧失衡,平衡因子变为 1,subRL 平衡,为 0(这其实就是动图展示的情况)
情况三:新节点插入至右子树的左侧后,subRL 平衡因子变为 1,证明 新节点插入至 subRL 的右边,并且左边没有东西,旋转后,parent 没有分到节点,subR 分到了,subRL 为平衡,因此 parent 的平衡因子为 -1,subR 和 subRL 的平衡因子都是 0
经过这样分析后,就能得到代码中的判断逻辑
注意: 先要右单旋,才左单旋;平衡因子的更新需要分类讨论
2-6 🥓左右双旋
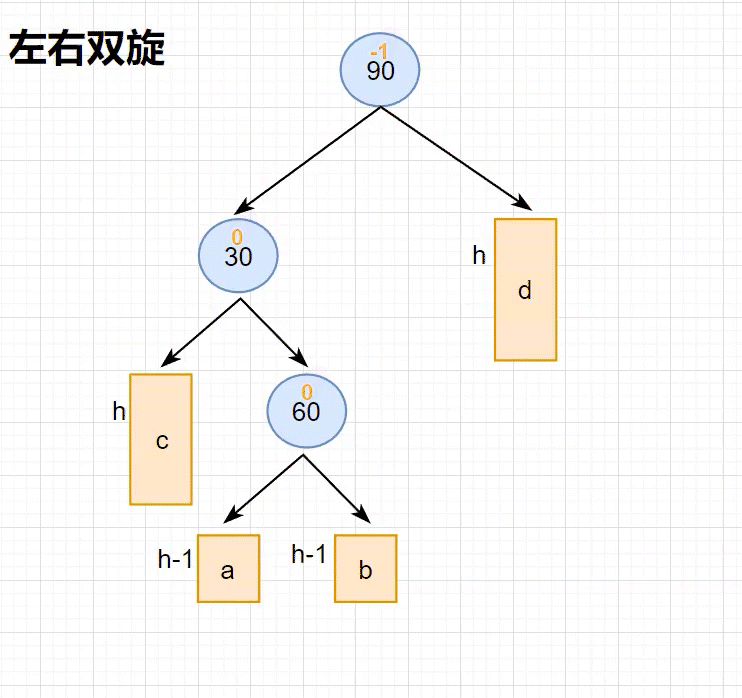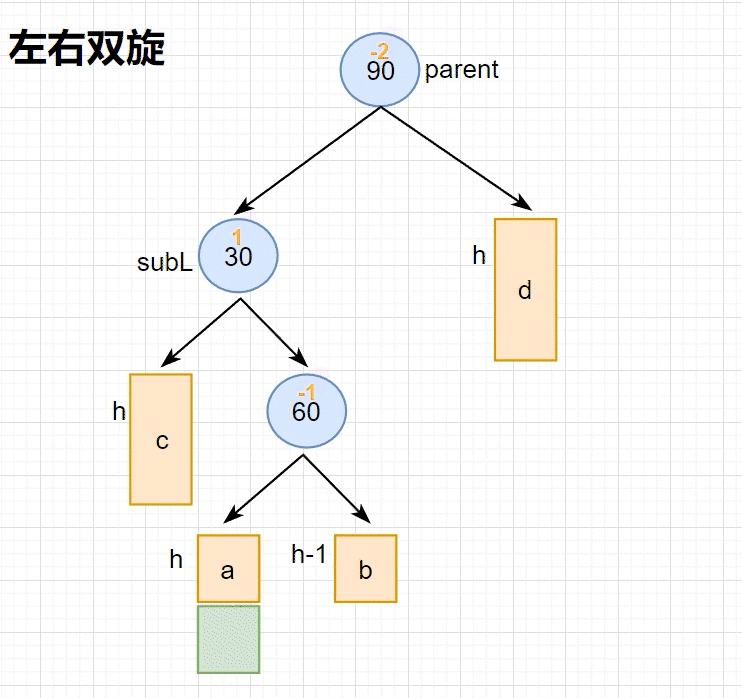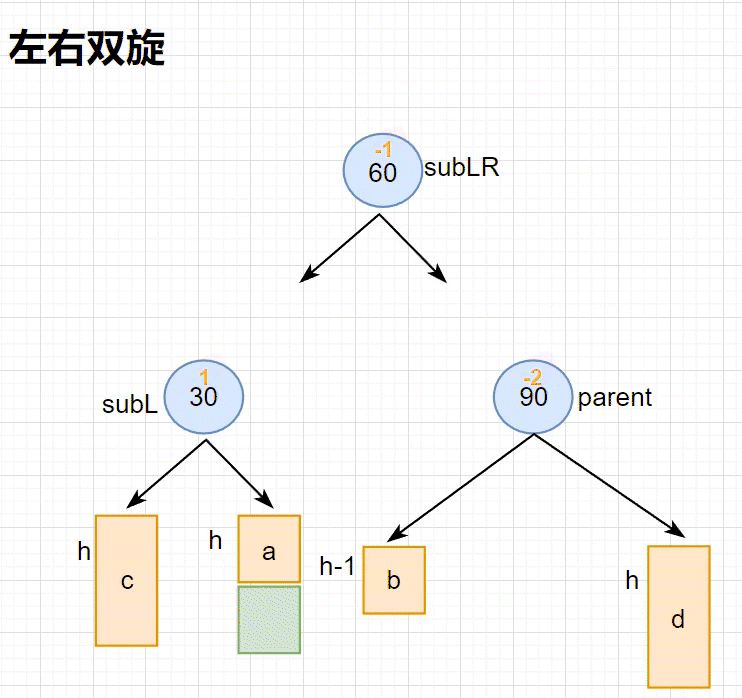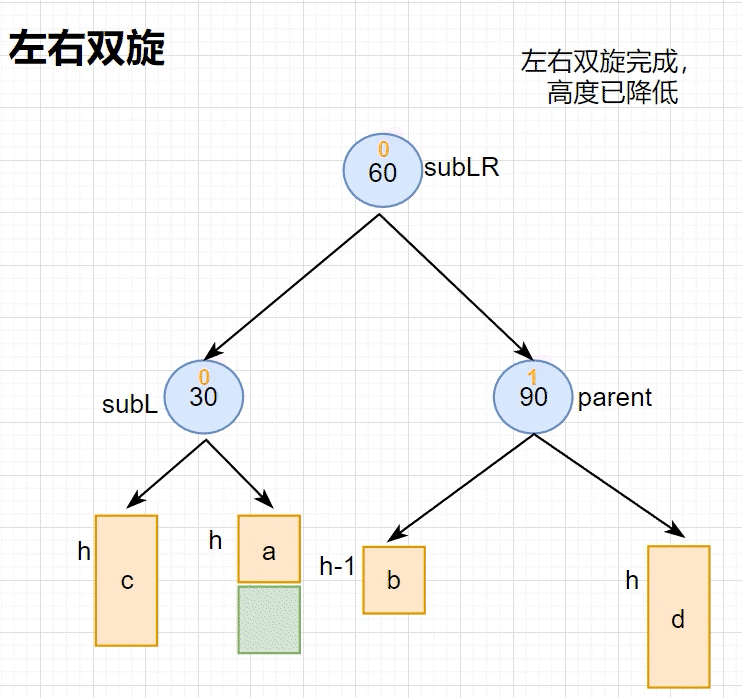
通过下面两图可以看到,左边⾼时,如果插⼊位置不是在a⼦树,⽽是插⼊在 b ⼦树,b⼦树⾼度从h变成h+1,引发旋转,右单旋⽆法解决问题,右单旋后,我们的树依旧不平衡。右单旋解决的纯粹的左边⾼,但是插⼊在b⼦树中,10为跟的⼦树不再是单纯的左边⾼,对于10是左边⾼,但是对于5是右边⾼,需要⽤两次旋转才能解决,以5为旋转点进⾏⼀个左单旋,以10为旋转点进⾏⼀个右单旋,这棵树这棵树就平衡了。
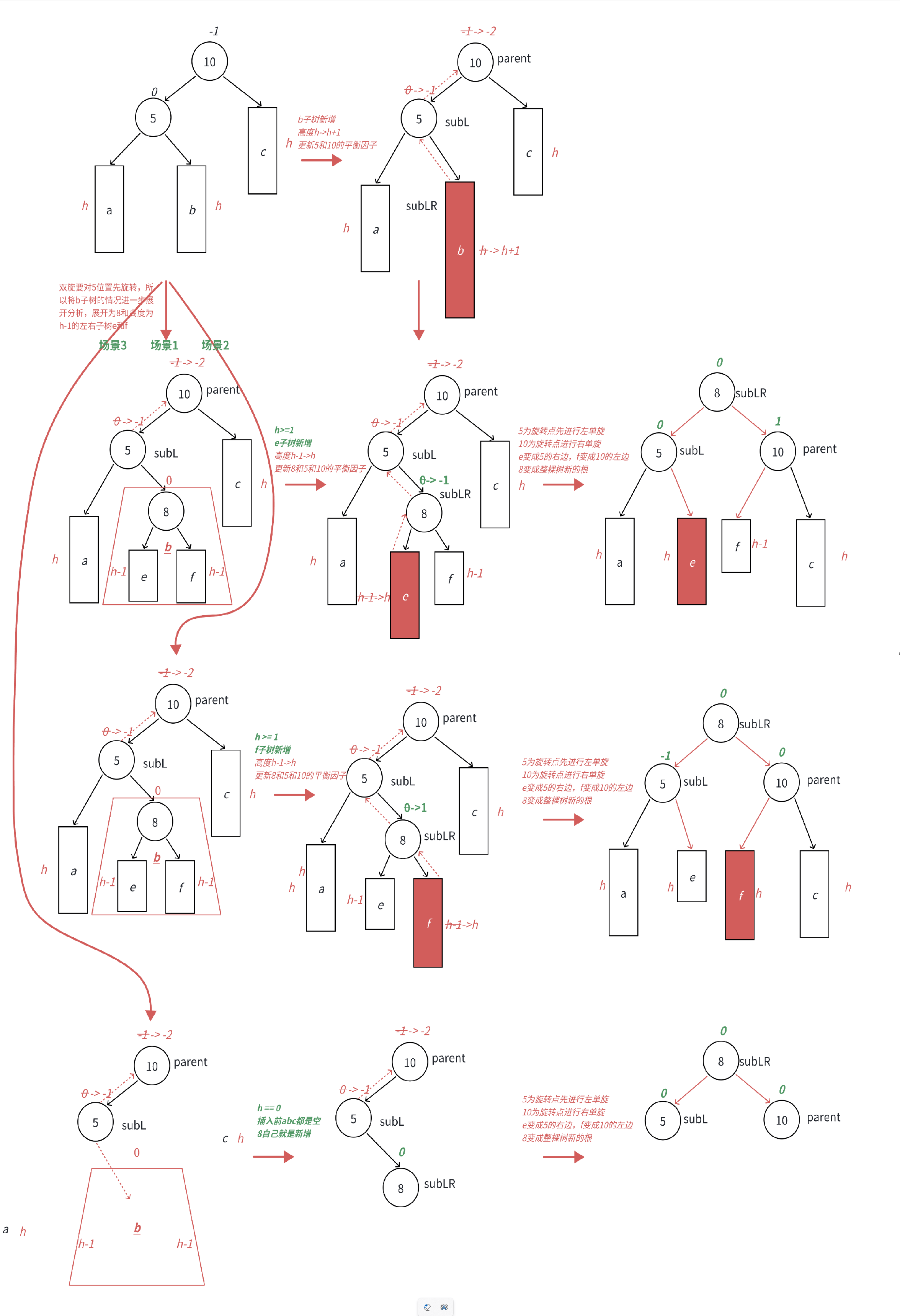
•上面两图分别为左右双旋中h==0和h==1具体场景分析,下⾯我们将a/b/c⼦树抽象为⾼度h的AVL⼦树进⾏分析,另外我们需要把b⼦树的细节进⼀步展开为8和左⼦树⾼度为h-1的e和f⼦树,因为我们要对b的⽗亲5为旋转点进⾏左单旋,左单旋需要动b树中的左⼦树。b⼦树中新增结点的位置不同,平衡因⼦更新的细节也不同,通过观察8的平衡因⼦不同,这⾥我们要分三个场景讨论。
•场景1:h >= 1时,新增结点插⼊在e⼦树,e⼦树⾼度从h-1并为h并不断更新8->5->10平衡因⼦,引发旋转,其中8的平衡因⼦为-1,旋转后8和5平衡因⼦为0,10平衡因⼦为1。
•场景2:h >= 1时,新增结点插⼊在f⼦树,f⼦树⾼度从h-1变为h并不断更新8->5->10平衡因⼦,引发旋转,其中8的平衡因⼦为1,旋转后8和10平衡因⼦为0,5平衡因⼦为-1。
•场景3:h == 0时,a/b/c都是空树,b⾃⼰就是⼀个新增结点,不断更新5->10平衡因⼦,引发旋转,其中8的平衡因⼦为0,旋转后8和10和5平衡因⼦均为0。
当节点插入至 左子树的右侧 时,会触发 左右双旋,需要 先进行 左单旋,再进行 右单旋 才能降低高度
cpp//左右双旋 void RotateLR(Node* parent) { Node* subL = parent->_left; Node* subLR = subL->_right; int BF = subLR->_bf; //先左单旋 RotateL(subL); //再右单旋 RotateR(parent); //根据不同的情况更新平衡因子 if (BF == 0) { parent->_bf = subL->_bf = 0; } else if (BF == 1) { parent->_bf = 0; subL->_bf = -1; subLR->_bf = 0; } else if (BF == -1) { parent->_bf = 1; subL->_bf = 0; subLR->_bf = 0; } else { //非法情况 std::cerr << "此处的平衡因子出现异常!" << std::endl; assert(false); //直接断言报错 } }左右双旋 的 旋转 流程如下图所示(动图)
左右双旋 逻辑:
- 确定 parent、subL、subLR
- 将 subLR 的右子树托付给 parent,左子树托付给 subL
- subLR 向上提,整体高度下降
- 需要特别注意平衡因子的调整
调整逻辑与 右左双旋 差不多
情况一:新节点插入至左子树右侧后,subLR 平衡因子变为 0,此时树变得更加平衡了,因此 parent、subL、subLR 三者的平衡因子都为 0
情况二:新节点插入至左子树的右侧后,subLR 平衡因子变为 -1,证明 新节点插入至 subLR 的左边,并且右边没有东西,旋转后,将新节点托付给 subL 后,subL 变得平衡了,但 parent 因没有分到节点,因此导致其右侧失衡,平衡因子变为 1,subLR 平衡,为 0
情况三:新节点插入至左子树的右侧后,subLR 平衡因子变为 1,证明 新节点插入至 subLR 右边,并且左边没有东西,旋转后,subL 没有分到节点,parent 分到了,subLR 为平衡,因此 subL 的平衡因子为 -1,parent 和 subLR 的平衡因子都是 0(动图中演示的就是情况三)
总的来说,双旋 需要慎重考虑 平衡因子 的调整
2-7 🥚注意事项及调试技巧
在编写 AVL 树的旋转操作时,涉及众多 相等 == 判断,一定要检查仔细,不能写成 赋值 =
当前 AVL 树为 三叉链结构,在调整左右子树链接关系时,也需要对 父指针 进行调整
单旋转后,涉事节点的平衡因子都为 0
双旋转后,涉事节点的平衡因子需要分类讨论
AVL 的操作较多,仅仅一个 插入 操作就需要近
300行代码,所以在 面(shou)试(si) 时,一定要把情况分析情况
- 插入至 右右 时,左单旋
- 插入至 左左 时,右单旋
- 插入至 右左 时,右左双旋
- 插入至 左右 时,左右双旋
掌握 AVL 树的旋转操作,对后面的 红黑树 学习有帮助
如果写完插入操作后,测试发现了问题,可以借助以下调试技巧 Debug
- 将出问题的数据,自己按照旋转逻辑,画图分析一遍
- 然后进入出问题的前一步操作,通过监视窗口查看树的结构是否符合预期
- 如果不符合,就往前排查
- 如果实在想不清楚旋转逻辑,可以借助 抽象图 进行分析
建议还是对 判断相等 == 进行着重检查,作为这里的高频问题,比较难调试出结果,扫视排查就简单多了(已经有多位同学在编写
AVL树旋转部分代码时,出现此问题)将 AVL 树的 四种旋转情况 分析透彻后,就已经完成绝大部分工作了
关于 AVL 树详细操作可以参考这篇 Blog:《AVL树(动图详解)》
三、😂AVL树的合法性检验
3-1 🍳检验依据
如何检验自己的 AVL 树是否合法? 答案是通过平衡因子检查
平衡因子 反映的是 左右子树高度之差 ,计算出 左右子树高度之差 与当前节点的 平衡因子 进行比对,如果发现不同,则说明 AVL 树 非法
或者如果当前节点的 平衡因子 取值范围不在 [-1, 1] 内,也可以判断 非法
3-2 🧇检验方法
统计 二叉树子树高度 很简单,只需要在 检验合法性函数 中调用即可
cpp//验证是否为 AVL 树 bool IsAVLTree() { return _IsAVLTree(_root); } //获取高度 size_t getHeight() { return _getHeight(_root); } bool _IsAVLTree(Node* root) { if (root == nullptr) return true; //计算左右子树的高度 size_t leftTreeH = _getHeight(root->_left); size_t rightTreeH = _getHeight(root->_right); //计算差值 int diff = rightTreeH - leftTreeH; if (diff != root->_bf || root->_bf < -1 || root->_bf > 1) { std::cerr << "当前节点出现了问题: " << root->_kv.first<< " | " << root->_bf << std::endl; return false; } return _IsAVLTree(root->_left) && _IsAVLTree(root->_right); } size_t _getHeight(Node* root) { if (root == nullptr) return 0; size_t leftH = _getHeight(root->_left); size_t rightH = _getHeight(root->_right); return 1 + std::max(leftH, rightH); }通过一段简单的代码,随机插入
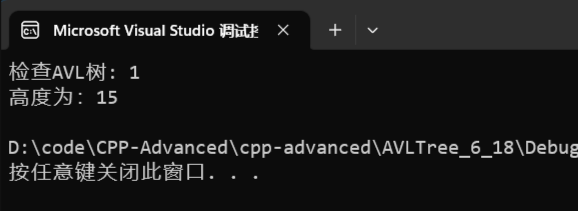
10000个节点,判断 是否合法 及当 AVL 树的 高度
cppvoid AVLTreeTest2() { srand((size_t)time(NULL)); AVLTree<int, int> av; for (int i = 0; i < 10000; i++) { int val = rand() % 10000 + i; av.Insert(val, val); } cout << "检查AVL树: " << av.IsAVLTree() << endl << "高度为:" << av.getHeight() << endl; }鉴定为 合法 ,并且高度仅有 15,约为 2^14 即 1600+ 的容量
AVL 树是一棵十分自律的树,即使在数据量如此之大的情况下,也能很好的控制高度
3-3 🥞AVL树的性能
AVL 树是一棵 绝对平衡 的二叉树,对高度的控制极为苛刻,稍微有点退化的趋势,都要被旋转调整,这样做的好处是 严格控制了查询的时间,查询速度极快,约为 logN
但是过度苛刻也会带来一定的负面影响,比如涉及一些 结构修改 的操作时,性能非常低下,更差的是在 删除 时,因为从任意位置破坏了 二叉搜索树 及 AVL 树的属性 ,有可能会引发连锁旋转反应,导致一直 旋转 至 根 的位置(旋转比较浪费时间)
AVL 树性能很优秀,如果在存储大量不需要修改的静态数据时,用 AVL 树是极好的,但在大多数场景中,用不到这么极限的性能,此时就需要一种 和
AVL树差不多,但又没有那么严格 的 平衡二叉搜索树 了而这种 平衡二叉搜索树 就是数据结构中大名鼎鼎的大哥:红黑树,关于 红黑树 的天才设计将在下文中介绍,值得一提的是 红黑树在减少旋转次数的同时,还能做到与 AVL 树的差距至多不超过 2 倍 ,这是非常牛叉的设计,依赖于 颜色:红 与 黑
📖源码
本文中涉及的代码:《AVL 树博客》
结束语
以上就是我对于【C++】STL 学习------「AVL树」的理解
感谢你的三连支持!!!