目录
[2.1 AVL的结构](#2.1 AVL的结构)
[2.2 AVL的插入](#2.2 AVL的插入)
[2.3 AVL的查询](#2.3 AVL的查询)
[2.4 AVL的平衡检测](#2.4 AVL的平衡检测)
一、AVL树的概念和特性
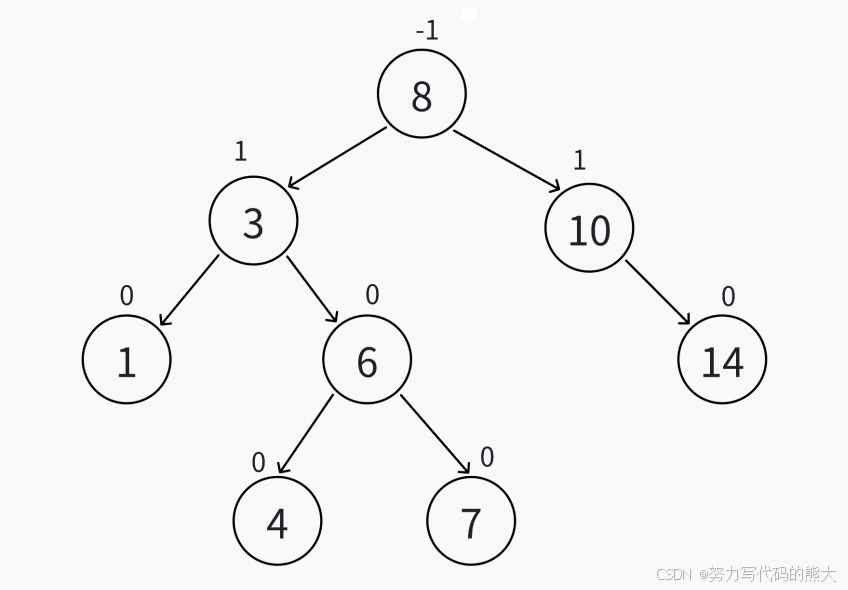
AVL树是最先发明的自平衡⼆叉查找树,AVL是⼀颗空树,或者具备下列性质的⼆叉搜索树:它的 左右子树都是AVL树,且左右子树的高度差的绝对值不超过1。AVL树是⼀颗高度平衡搜索⼆叉树,通过控制⾼度差去控制平衡。
AVL通过设置平衡因子使得其高度差绝对值不超过1。这里就需要 控制平衡因子为-1、1和0 这三个值。
正是因为这个特性他的树结构类似于完全二叉树,这使得和我们上一个博客中的二叉搜索树能够更加高效,增删查改的效率为
。
二、AVL的实现
2.1 AVL的结构
根据我们刚刚讲的概念和特性,我们可以写出AVL的结构,内部有一个左右指针、key、平衡因子和父节点(主要是修改平衡因子的作用)。
cpp
//AVL结点结构
template<class K,class V>
struct AVLNode
{
pair<K, V> _kv; //数据
AVLNode<K, V>* _left; //左孩子
AVLNode<K, V>* _right; //右孩子
AVLNode<K, V>* _parent; //父节点
int _bf = 0; //平衡因子
//初始化
AVLNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
,_parent(nullptr)
{ }
};
//定义AVL树结构
template<class K,class V>
class AVLTree
{
typedef AVLNode<K, V> Node;
public:
//初始化
AVLTree(Node* root = nullptr)
:_root(root)
{ }
private:
Node* _root;
};2.2 AVL的插入
大体插入
大体插入思路这里就和我们上个博客类似,就是判断key大小。这里我就不一一赘述了,感兴趣可以看我这个博客(二叉搜索树:数据宇宙中的秩序法典与高效检索圣殿-CSDN博客)。
cpp
//插入(以右为正,以右为大)
bool insert(const pair<K, V>& kv)
{
//判断根是否为空
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//比cur大,往右棵树走
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
//比cur小,往左课树走
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
//相同
else
{
return false;
}
}
//找到空位置了
Node* node = new Node(kv);
//判断和父节点的大小
if (parent->_kv.first < kv.first)
{
parent->_right = node;
}
else
{
parent->_left = node;
}
//更新父节点
node->_parent = parent;
//更新平衡因子
while (parent)
{
//node为parent左孩子
if (parent->_left = node)
{
parent->_bf--;1
}
//右孩子
else
{
parent->_bf++;
}
//如果修改后结点为0(高度差不变,只改变一次parent)
if (parent->_bf == 0)
{
break;
}
//如果修改后结点为-1/1(往上修改每个parent的值)
else if (parent->_bf == -1 || parent->_bf == 1)
{
node = parent;
parent = parent->_parent;//体现parent作用
}
//如果为2/-2时候,需要旋转使其平衡
else
{
//旋转
break;
}
}
return true;
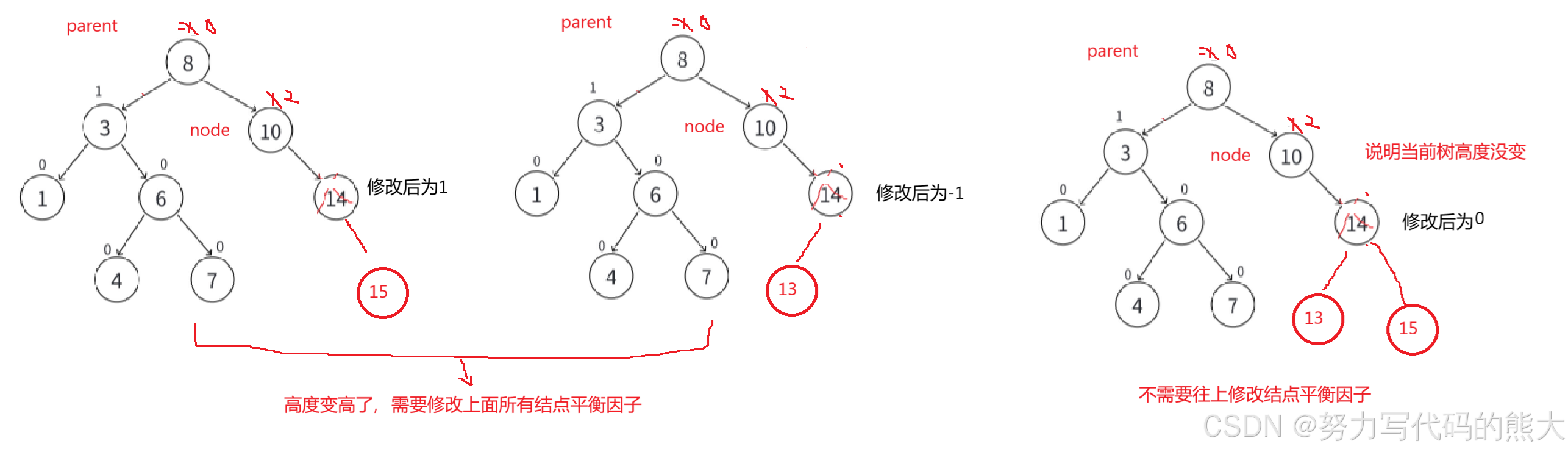
}这里关于我修改平衡因子的逻辑,我这里是寻找到当修改后平衡因子为0,就说明这当前这课树整体并没有增加高度,所以直接跳出循环没必要修改上面结点平衡因子,然后这里如果修改后为1/-1就说明这里修改增加高度了,就需要修改所有上面的结点平衡因子(根节点另一侧不用修改)
旋转
当我们遇到往上修改平衡因子后该平衡因子为-2/2的时候,这个时候我们不能不管,因为这里AVL平衡树就是依靠高度差为1来维持的平衡,我们这里解决的办法就是使用旋转,把侧向的结点通过旋转到另一侧。
旋转的规则:
- 保持搜索树的规则(左<根<右)
- 让旋转的树从不满⾜变平衡,其次降低旋转树的⾼度(使其变为-1/1/0)
旋转总共分为四种,左单旋/右单旋/左右双旋/右左双旋。
左单旋(图解)
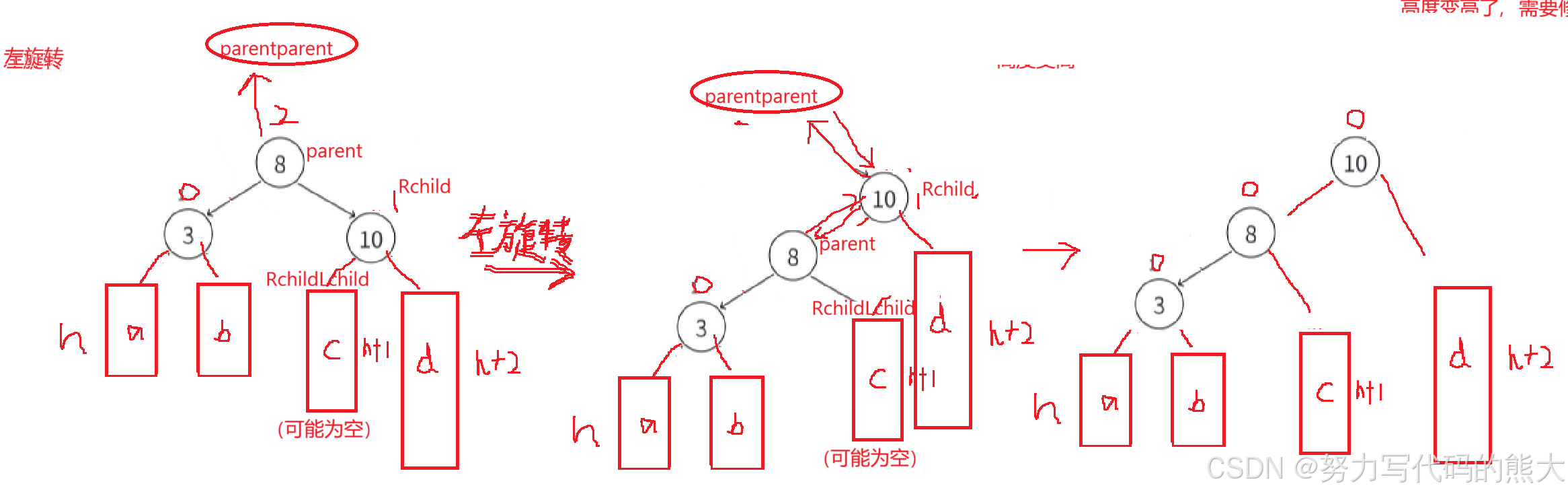
当我们遇到这种情况的时候就需要左旋转(往左边旋),这个情况是cur结点平衡因子为1,parent的平衡因子为2。
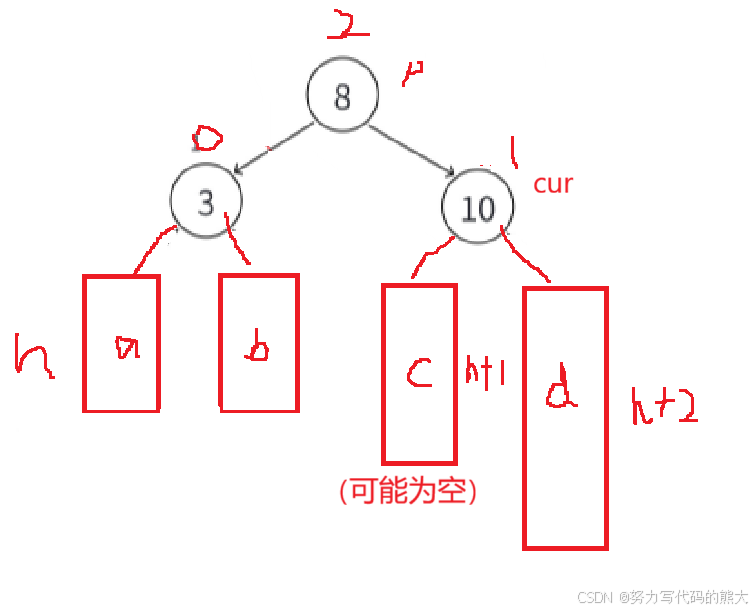
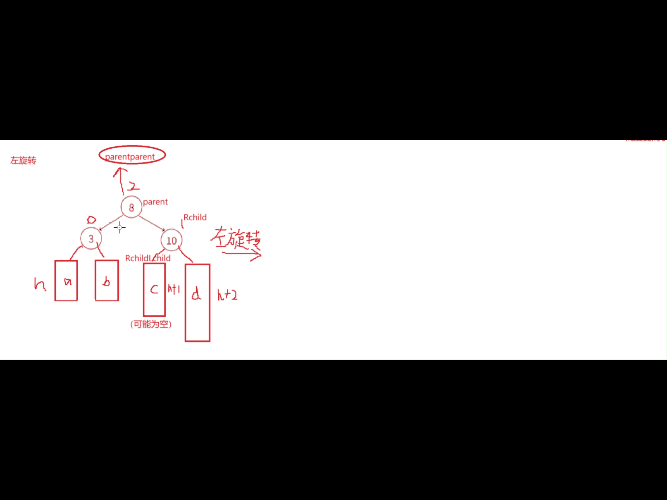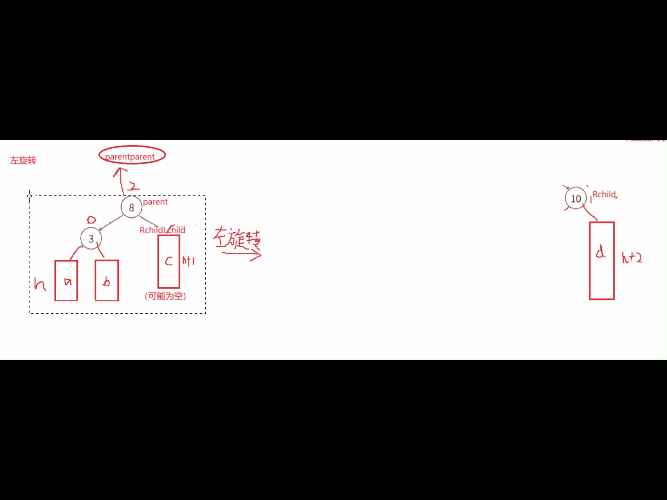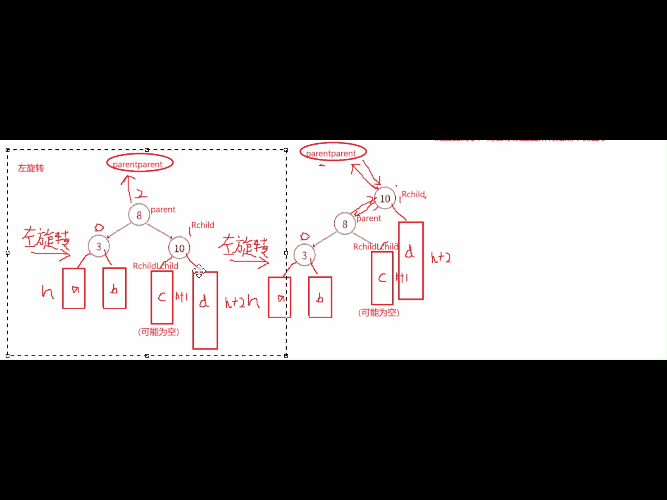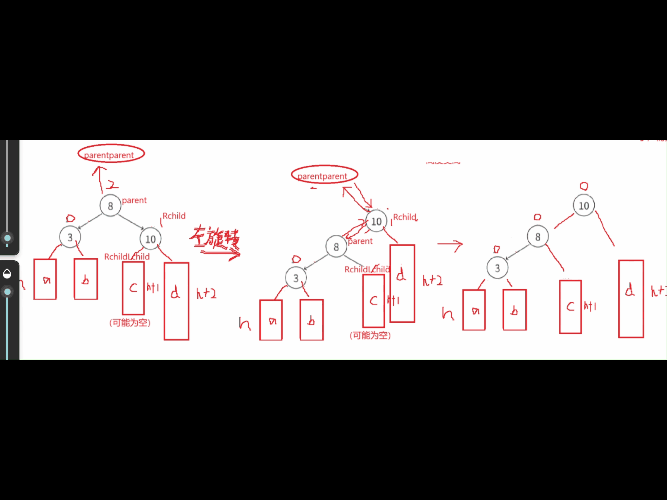
左单旋的旋转原理:就是通过把8这个结点进行往左下压,然后让10来继承8的位置,把C这课树成为8的右子树(肯定是比8大),在通过连接把10于8连接起来,这个过程必须连同结点的parent也更新。整个过程的代码思路就是先连接parent与cur右孩子的连接关系,然后再处理cur这个结点与parent的连接关系,最后处理parent的父节点与cur的连接关系。最后旋转后发现一个规律就是改变高度受到影响的平衡因子都为0了。
cpp
//左单旋
void RotateL(Node* parent)
{
Node* Rchild = parent->_right; //右孩子
Node* parentparent = parent->_parent; //父节点的父节点
Node* RchildLchild = Rchild->_left; //Rchild左孩子
//先处理parent与RchildLchild连接关系
if(RchildLchild)//可能为空,导致空指针解引用问题
RchildLchild->_parent = parent;
parent->_right = RchildLchild;
//处理Rchild与parent的关系
Rchild->_left = parent;
parent->_parent = Rchild;
//然后处理parentparent与Rchild的连接关系
//判断是否为根节点
if (parent == _root)
{
_root = Rchild;
Rchild->_parent = nullptr;//可读性,明确为空
}
else
{
//衔接Rchild与parentparent的关系
//判断Rchild是parentparent的左右孩子
if (parentparent->_left == parent)
{
parentparent->_left = Rchild;
}
else
{
parentparent->_right = Rchild;
}
Rchild->_parent = parentparent;//最后更新Rchild的父节点
}
//发现左旋转后,平衡因子也就完全平衡了都为0
parent->_bf = Rchild->_bf = 0;
}
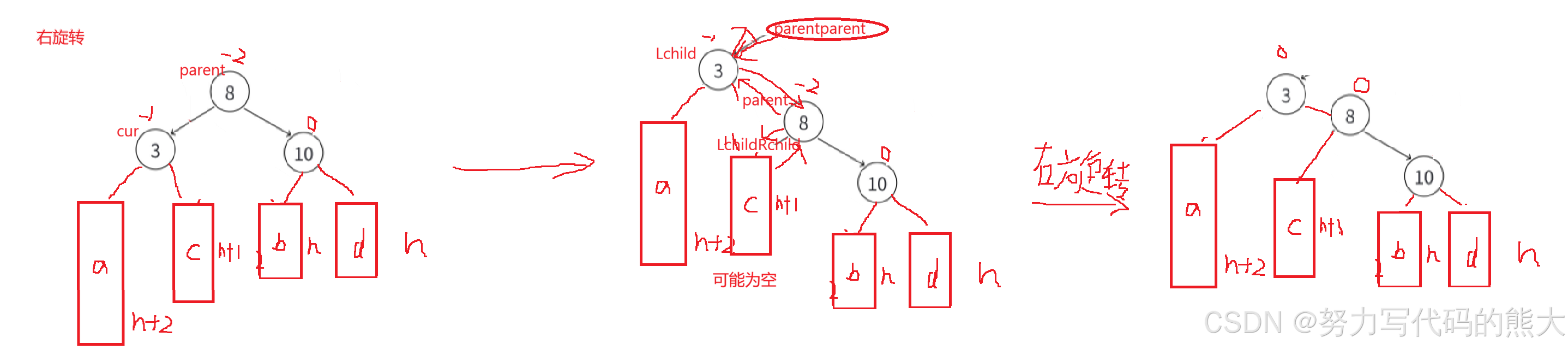
右单旋(图解)
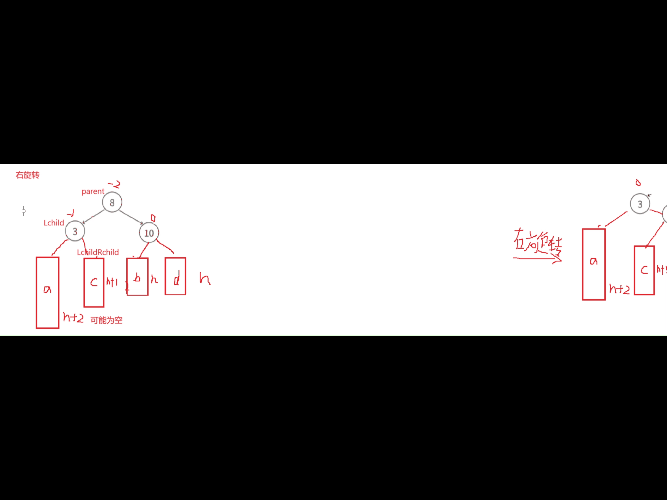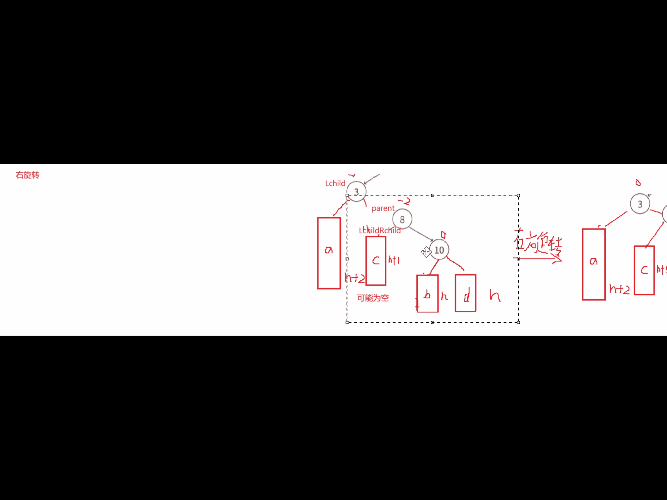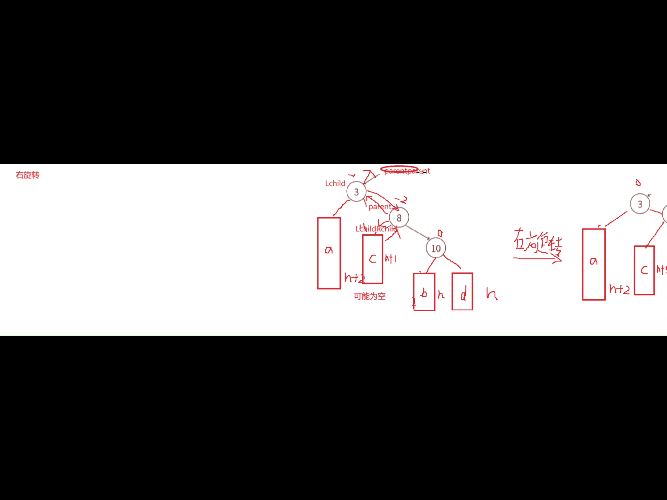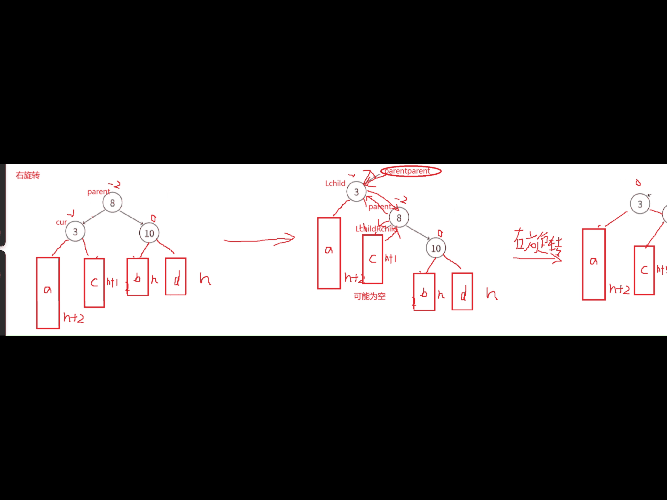
当我们遇到这种这种左棵树高度-右棵树高度为-2的时候,就需要进行右旋转,次数cur为-1。
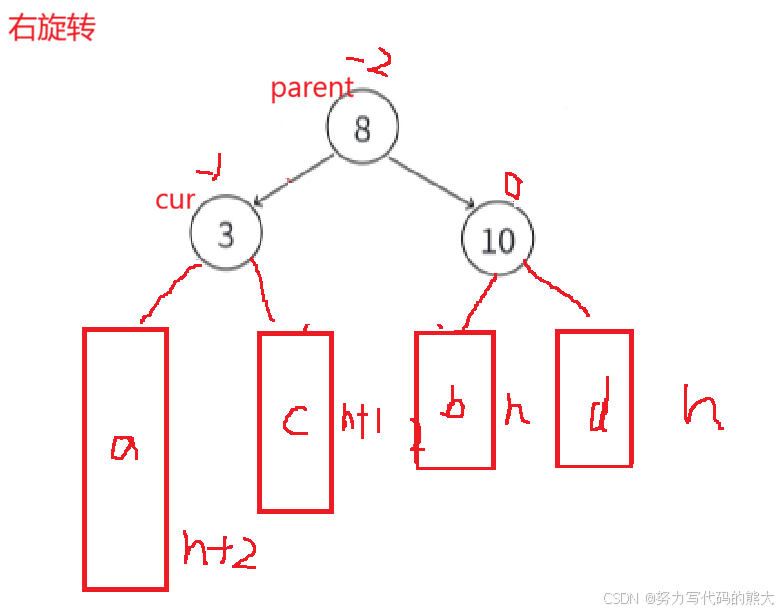
右单旋的原理和左单旋类似,这里是吧8往右下压,3去充当8的位置,然后让8下降应该位置,再把3的右子树给8连接起来,3与8连接起来,8与3的左孩子连接起来。代码思路就是先处理parent与cur左孩子的关系,然后再处理cur与parent的连接关系,最后处理cur与parent的父节点的连接关系 。发现无论是左旋转还是右旋转,最终我们都是把改变高度的结点的平衡因子都变为0了。
cpp
//右单旋
void RotateR(Node* parent)
{
Node* Lchild = parent->_left;
Node* LchildRchild = Lchild->_right;
Node* parentparent = parent->_parent;
//先连接与parent与LchildRchild的连接关系
if (LchildRchild)//可能为空,避免空指针解引用
LchildRchild->_parent = parent;
parent->_left = LchildRchild;
//再连接parent与Lchild的连接关系
Lchild->_right = parent;
parent->_parent = Lchild;
//最后连接parentparent与Lchild的关系
if (parent == _root)//为根
{
_root = Lchild;
Lchild->_parent = nullptr;//明确为空
}
else//不为根
{
//判断是parentparent的左右孩子
if (parentparent->_left == parent)
{
parentparent->_left = Lchild;
}
else
{
parentparent->_right = Lchild;
}
Lchild->_parent = parentparent;
}
//调整平衡因子
Lchild->_bf = parent->_bf = 0;
}
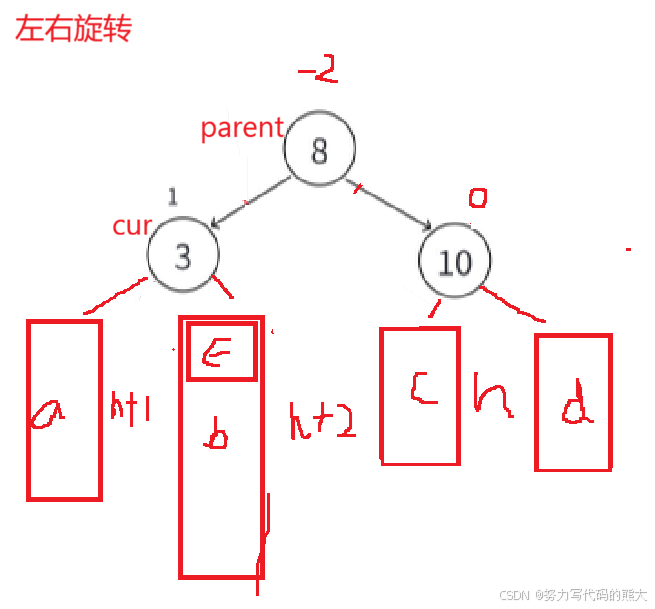
左右双旋(图解)
当我们遇到这种不是同一侧影响的高度差引起的不平衡情况,这个时候就需要左右双旋了,此时parent为-2,cur为1。
而这种情况又被分成3种情况分别讨论平衡因子。
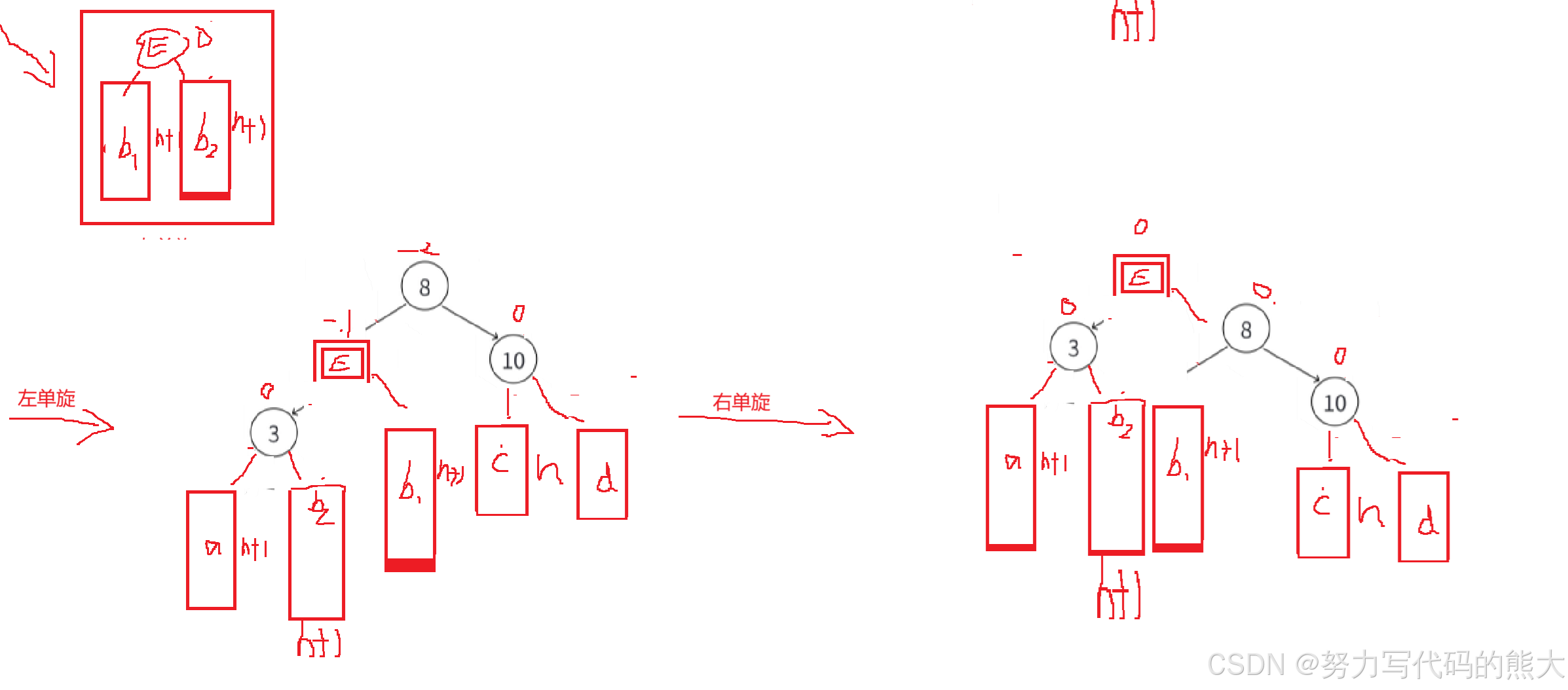
第一种:
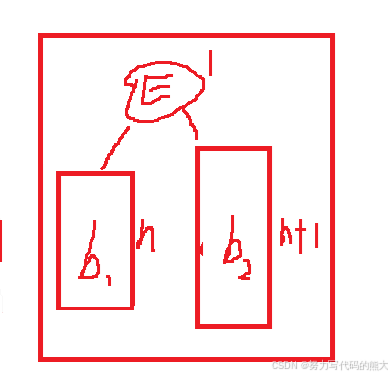
这情况我们需要考虑通过左单旋和右单旋,调整后因子全变为0了,但是这些双旋后,平衡因子不全是0,可能是-1/0/1这些情况,普通单旋是直接平衡为0,但是双旋不是。针对这种情况的分析,我们要结合图来分析通过左单旋和右单旋后,这里E中的两个子树h1,h2分别分到cur和parent中 ,这里的平衡因子的改变就是根据E中的平衡因子变化的,h1上的比h2高度小,cur的位置结点平衡因子就是-1,而h2比是决定高度的树,所以parent就是0。修改调整E为平衡因子0,cur的平衡因子为-1,parent的平衡因子为0。
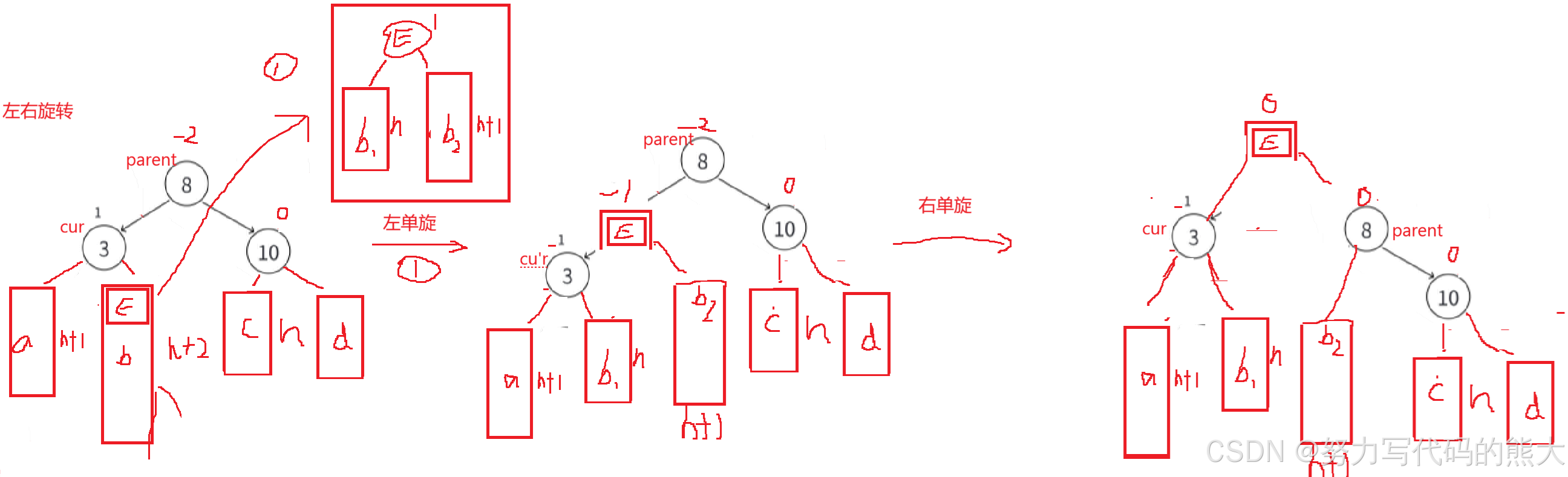
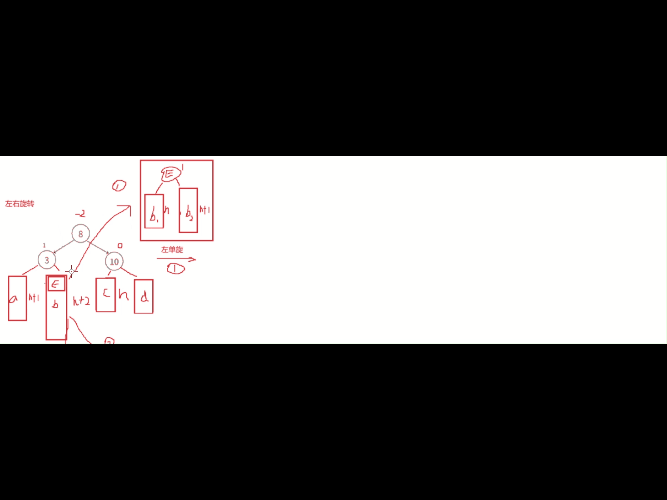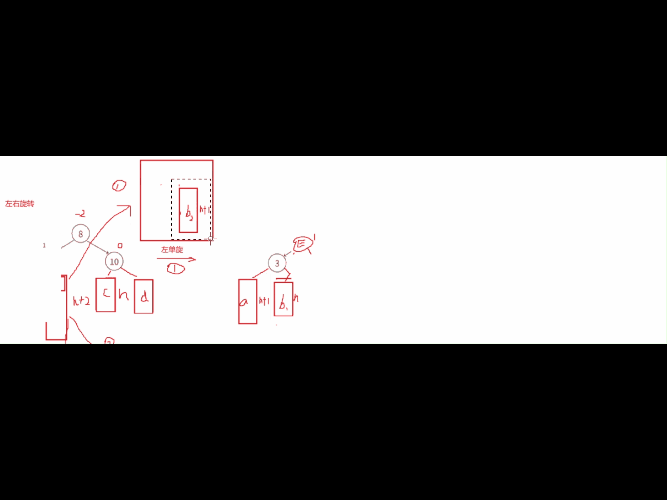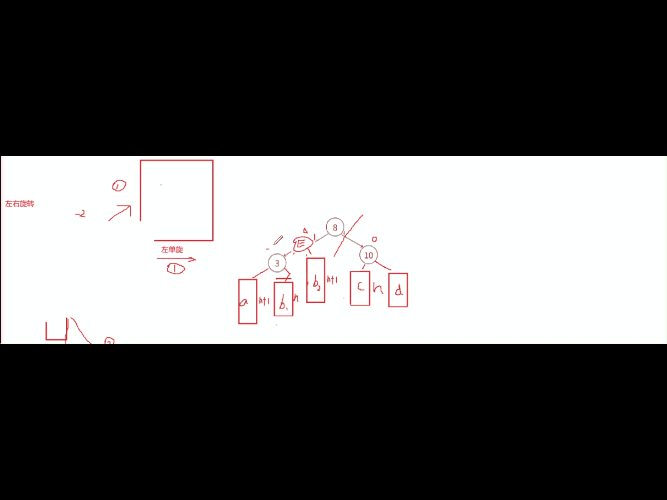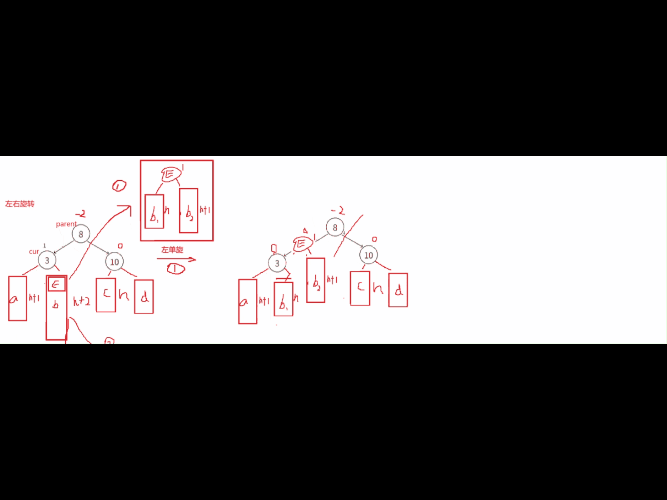
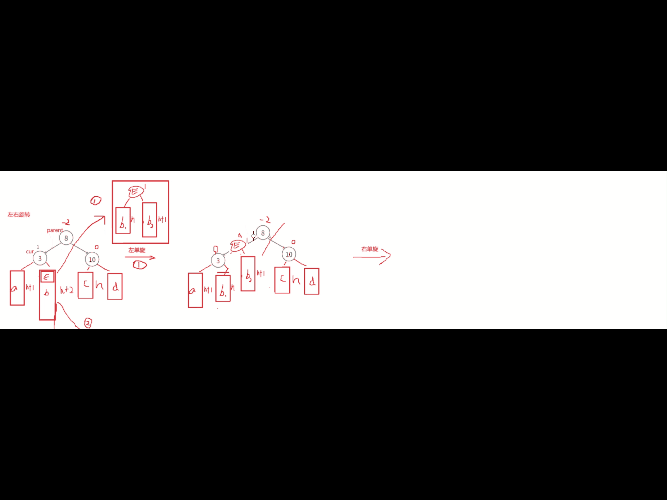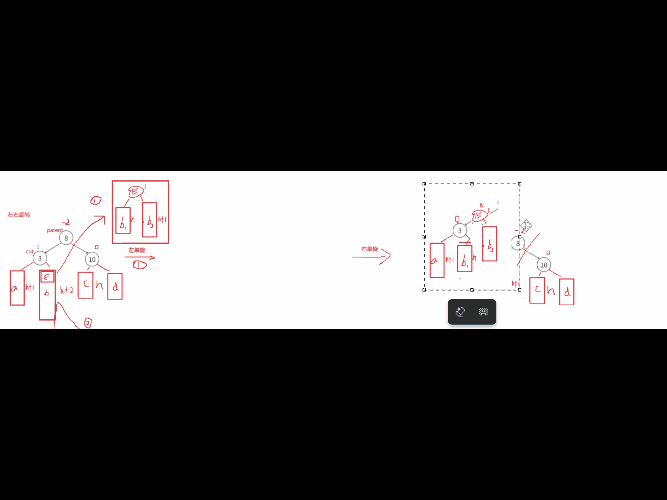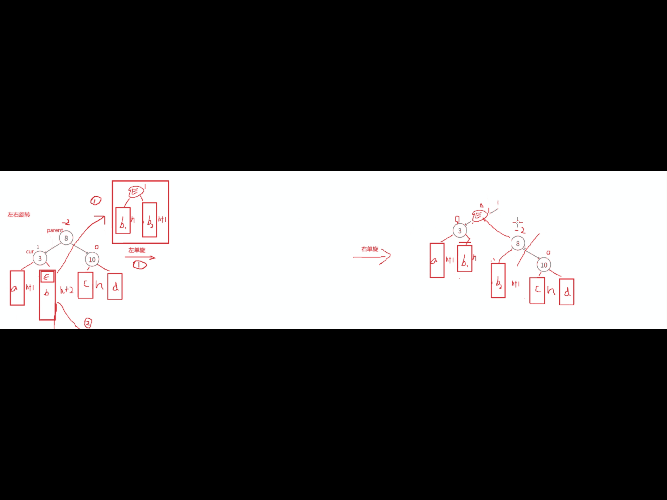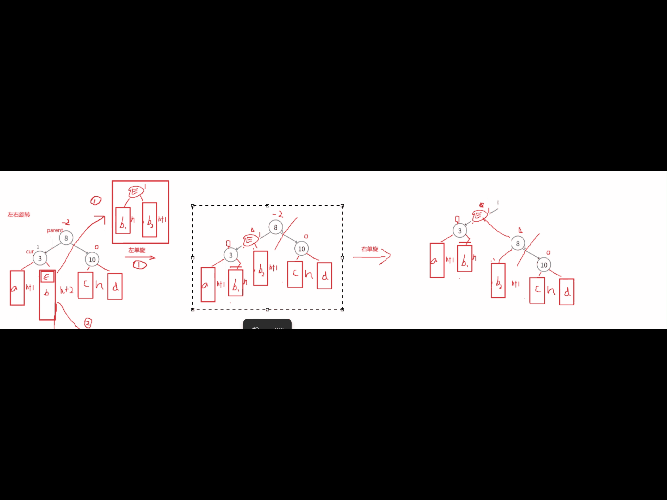
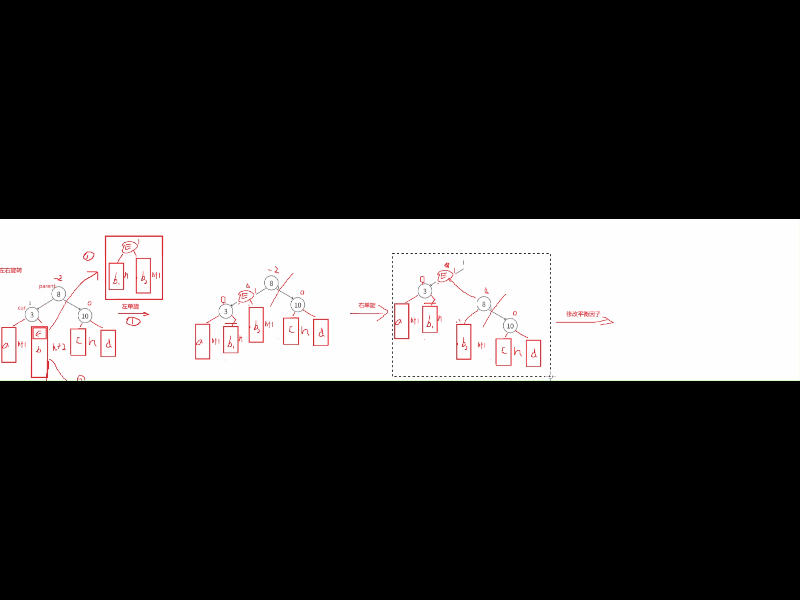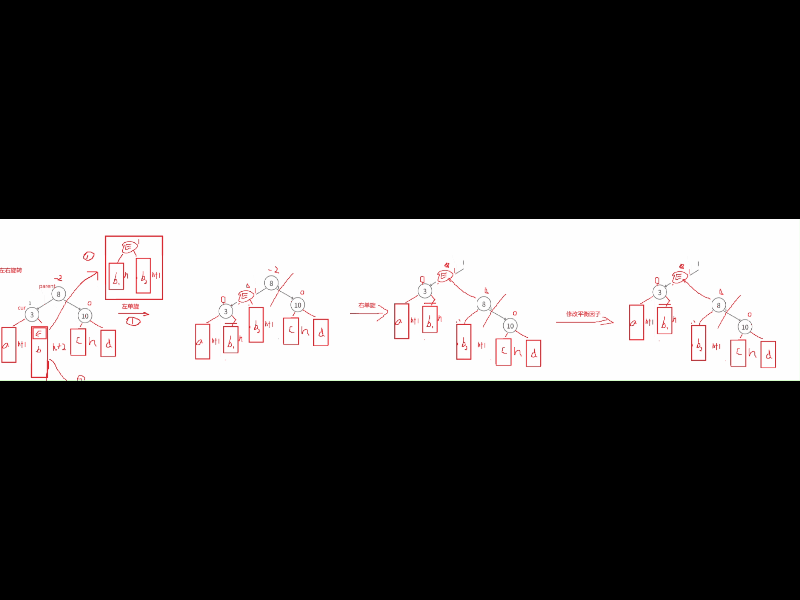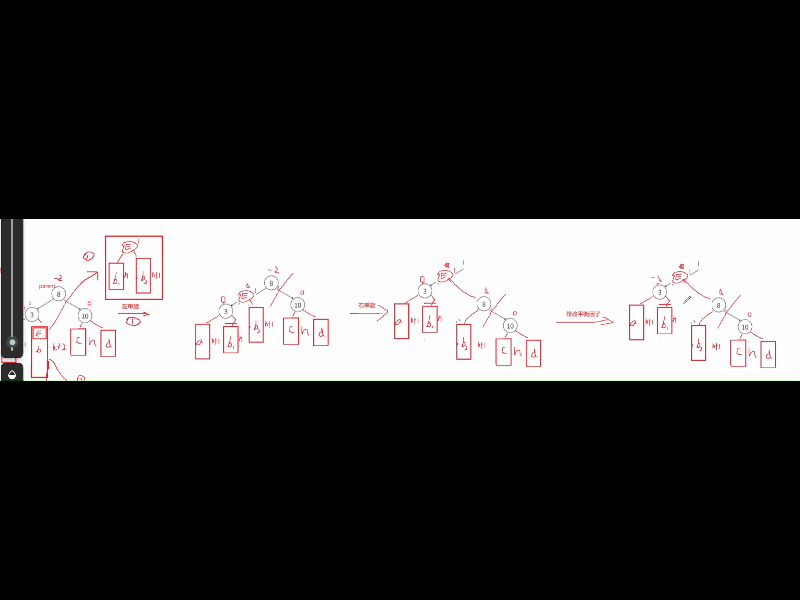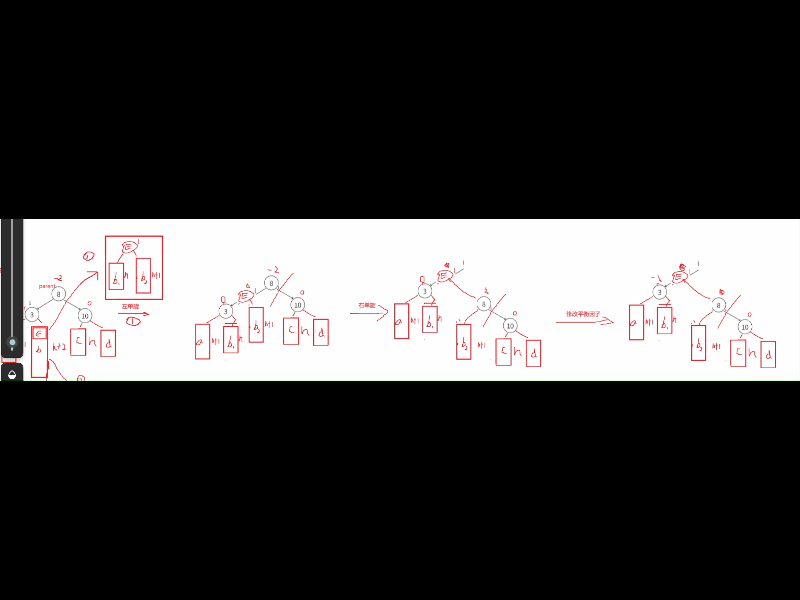

第二种:
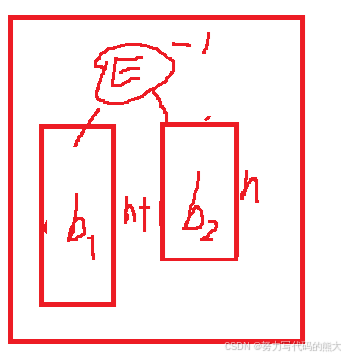
同理,和第一种的思路一样,只不过这里高度差偏向左侧,这里E的h1和h2分配到cur和parent中。都是先旋转,然后再调整平衡因子,调整E为平衡因子0,cur的平衡因子为0,parent的平衡因子为-1。
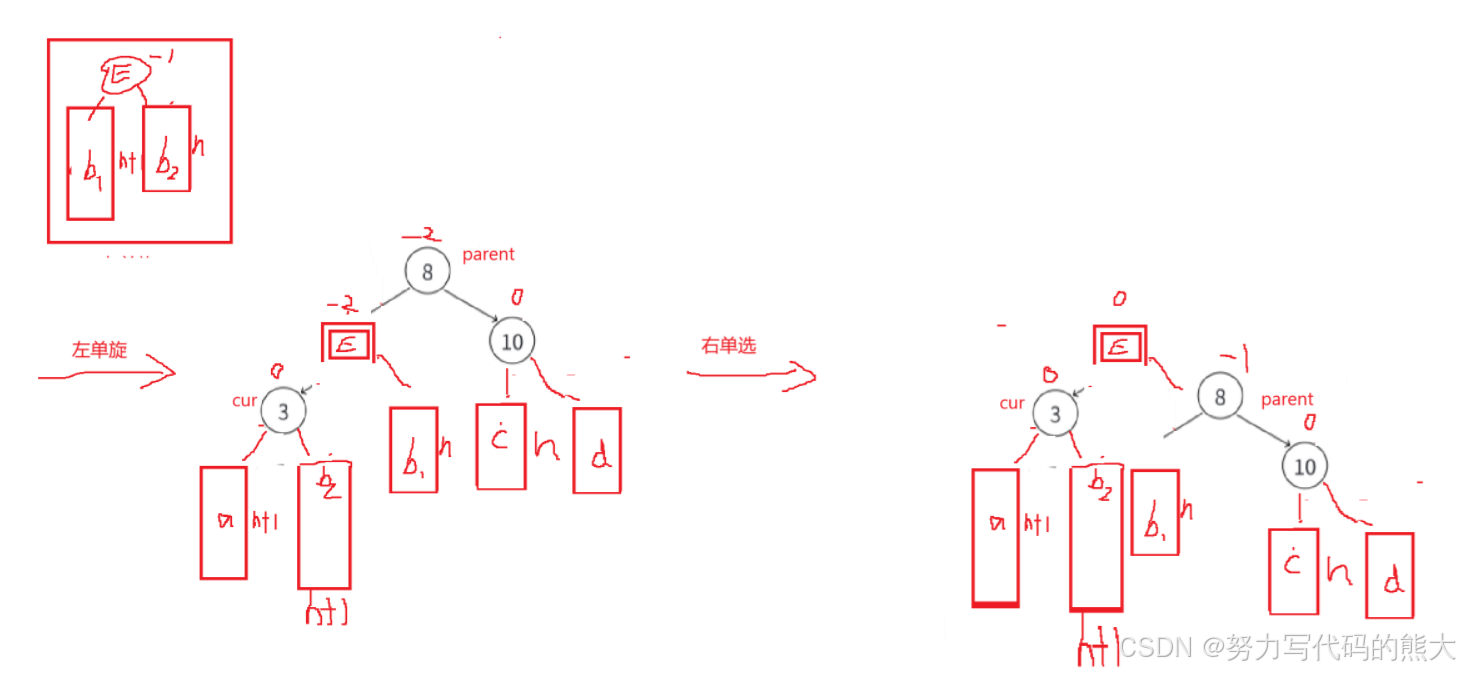
第三种:
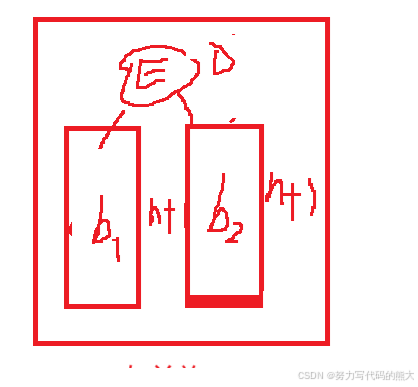
在这里因为E的平衡因子为0,通过左右双旋h1和h2分到cur和parent是得都为0。
cpp
void RotateLR(Node* parent)
{
Node* Lchild = parent->_left; //cur结点
Node* LchildRchild = Lchild->_right; //E结点
//提前记录E结点,防止旋转后为0。为后续修改平衡因子做铺垫
int E_bf = LchildRchild->_bf;
//先左单旋
RotateL(Lchild);
//然后右单旋
RotateR(parent);
//修改平衡因子
if (E_bf == 1)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = -1; //cur
parent->_bf = 0; //parent
}
else if(E_bf == -1)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = 0; //cur
parent->_bf = 1; //parent
}
else if (E_bf == 0)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = 0; //cur
parent->_bf = 0; //parent
}
//异常
else
{
assert(false);
}
}总结一下,其实这里的左右双旋其实就是控制平衡因子是重点,旋转过程不用在意。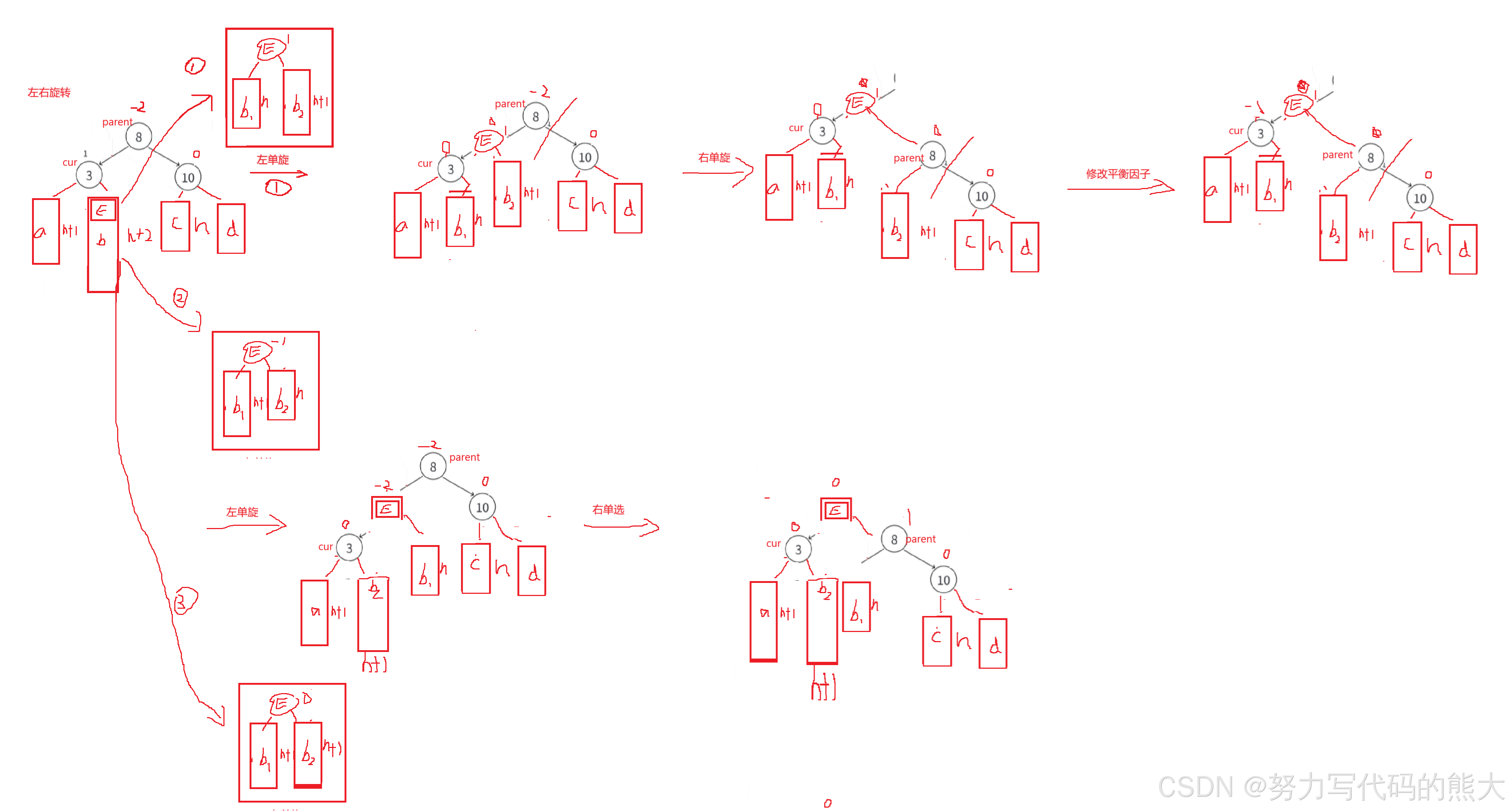
右左双旋
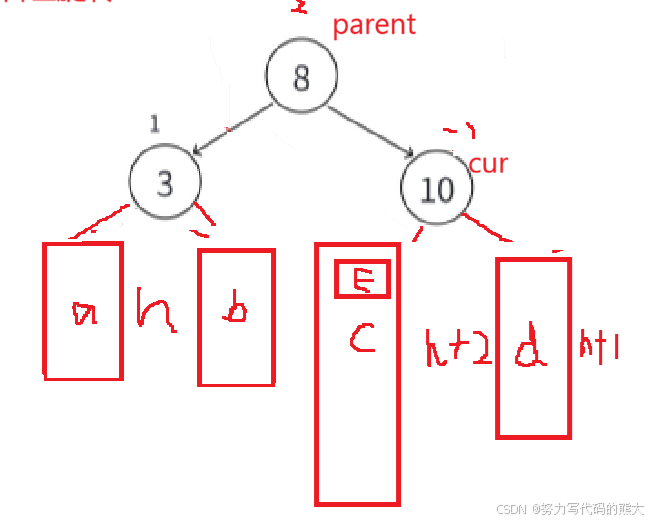
根据上面的左右双旋的思路,其实这两也是一样的,我就不一一用gif图解释了。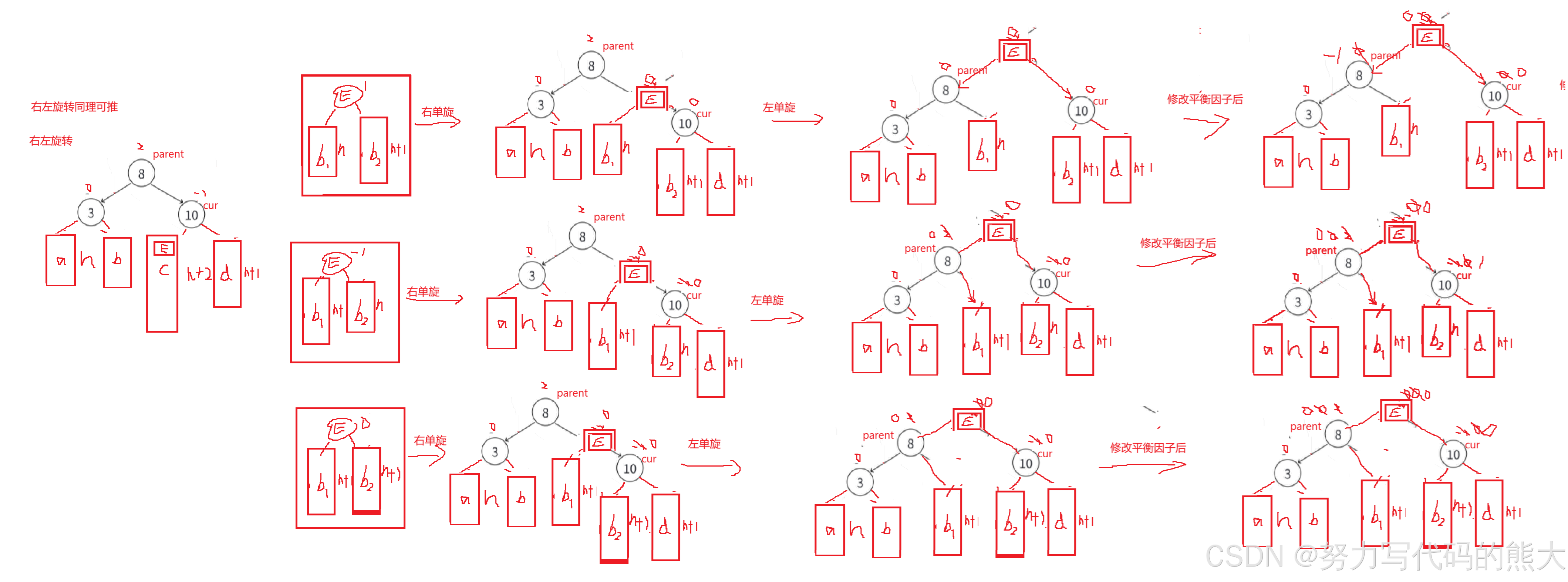
cpp
void RotateRL(Node* parent)
{
Node* Rchild = parent->_right; //cur结点
Node* RchildLchild = Rchild->_left; //E结点
int E_bf = RchildLchild->_bf; //E的结点
RotateR(Rchild);
RotateL(parent);
if (E_bf == 0)
{
Rchild->_bf = 0; //cur
RchildLchild->_bf = 0; //E
parent->_bf = 0; //parent
}
else if (E_bf == 1)
{
Rchild->_bf = 0; //cur
RchildLchild->_bf = 0; //E
parent->_bf = -1; //parent
}
else if (E_bf == -1)
{
Rchild->_bf = 1; //cur
RchildLchild->_bf = 0; //E
parent->_bf = 0; //parent
}
else
{
assert(false);
}
}完整代码
cpp
//插入(以右为正,以右为大)
bool insert(const pair<K, V>& kv)
{
//判断根是否为空
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//比cur大,往右棵树走
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
//比cur小,往左课树走
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
//相同
else
{
return false;
}
}
//找到空位置了
Node* node = new Node(kv);
//判断和父节点的大小
if (parent->_kv.first < kv.first)
{
parent->_right = node;
}
else
{
parent->_left = node;
}
//更新父节点
cur = node;
cur->_parent = parent;
//更新平衡因子
while (parent)
{
//node为parent左孩子
if (parent->_left == cur)
{
parent->_bf--;
}
//右孩子
else
{
parent->_bf++;
}
//如果修改后结点为0(高度差不变,只改变一次parent)
if (parent->_bf == 0)
{
break;
}
//如果修改后结点为-1/1(往上修改每个parent的值)
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = parent;
parent = parent->_parent;//体现parent作用
}
//如果为2/-2时候,需要旋转使其平衡
else
{
//旋转
//左单旋
if (parent->_bf == 2&&cur->_bf == 1 )
{
RotateL(parent);
}
//右单旋
else if (parent->_bf == 2 && cur->_bf == -1 )
{
RotateR(parent);
}
//左右双旋
else if (parent->_bf == -2 && cur->_bf == 1 )
{
RotateLR(parent);
}
//右左双旋
else if (parent->_bf == 2 && cur->_bf = -1 )
{
RotateRL(parent);
}
break;
}
}
return true;
}
//左单旋
void RotateL(Node* parent)
{
Node* Rchild = parent->_right; //右孩子
Node* parentparent = parent->_parent; //父节点的父节点
Node* RchildLchild = Rchild->_left; //Rchild左孩子
//先处理parent与RchildLchild连接关系
if(RchildLchild)//可能为空,导致空指针解引用问题
RchildLchild->_parent = parent;
parent->_right = RchildLchild;
//处理Rchild与parent的关系
Rchild->_left = parent;
parent->_parent = Rchild;
//然后处理parentparent与Rchild的连接关系
//判断是否为根节点
if (parent == _root)
{
_root = Rchild;
Rchild->_parent = nullptr;//可读性,明确为空
}
else
{
//衔接Rchild与parentparent的关系
//判断Rchild是parentparent的左右孩子
if (parentparent->_left == parent)
{
parentparent->_left = Rchild;
}
else
{
parentparent->_right = Rchild;
}
Rchild->_parent = parentparent;//最后更新Rchild的父节点
}
//发现左旋转后,平衡因子也就完全平衡了都为0
parent->_bf = Rchild->_bf = 0;
}
//右单旋
void RotateR(Node* parent)
{
Node* Lchild = parent->_left;
Node* LchildRchild = Lchild->_right;
Node* parentparent = parent->_parent;
//先连接与parent与LchildRchild的连接关系
if (LchildRchild)//可能为空,避免空指针解引用
LchildRchild->_parent = parent;
parent->_left = LchildRchild;
//再连接parent与Lchild的连接关系
Lchild->_right = parent;
parent->_parent = Lchild;
//最后连接parentparent与Lchild的关系
if (parent == _root)//为根
{
_root = Lchild;
Lchild->_parent = nullptr;//明确为空
}
else//不为根
{
//判断是parentparent的左右孩子
if (parentparent->_left == parent)
{
parentparent->_left = Lchild;
}
else
{
parentparent->_right = Lchild;
}
Lchild->_parent = parentparent;
}
//调整平衡因子
Lchild->_bf = parent->_bf = 0;
}
//左右双旋
void RotateLR(Node* parent)
{
Node* Lchild = parent->_left; //cur结点
Node* LchildRchild = Lchild->_right; //E结点
//提前记录E结点,防止旋转后为0。为后续修改平衡因子做铺垫
int E_bf = LchildRchild->_bf;
//先左单旋
RotateL(Lchild);
//然后右单旋
RotateR(parent);
//修改平衡因子
if (E_bf == 1)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = -1; //cur
parent->_bf = 0; //parent
}
else if(E_bf == -1)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = 0; //cur
parent->_bf = 1; //parent
}
else if (E_bf == 0)
{
LchildRchild->_bf = 0; //E
Lchild->_bf = 0; //cur
parent->_bf = 0; //parent
}
//异常
else
{
assert(false);
}
}
//右左双旋
void RotateRL(Node* parent)
{
Node* Rchild = parent->_right; //cur结点
Node* RchildLchild = Rchild->_left; //E结点
int E_bf = RchildLchild->_bf; //E的结点
RotateR(Rchild);
RotateL(parent);
if (E_bf == 0)
{
Rchild->_bf = 0; //cur
RchildLchild->_bf = 0; //E
parent->_bf = 0; //parent
}
else if (E_bf == 1)
{
Rchild->_bf = 0; //cur
RchildLchild->_bf = 0; //E
parent->_bf = -1; //parent
}
else if (E_bf == -1)
{
Rchild->_bf = 1; //cur
RchildLchild->_bf = 0; //E
parent->_bf = 0; //parent
}
else
{
assert(false);
}
}2.3 AVL的查询
查询逻辑就很简单了,和上一篇博客中的查询是类似的几乎一模一样。
cpp
//查询
Node* Find(const k& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first > key)
{
cur = cur->_left;
}
else if (cur->_kv.first < key)
{
cur = cur->right;
}
else
{
return cur;
}
return nullptr;
}
}2.4 AVL的平衡检测
关于AVL的树检查,我们这里是通过计算比较高度个数和平衡因子的对比来判断是否平衡,且平衡因子是否有误。
cpp
bool _IsBalanceTree(Node* root)
{
//递归结束条件
if (root == nullptr)
return true;
//先计算每棵树的左右高度差
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
//计算高度差
int root_bf = rightHeight - leftHeight;//以右为正
//只需要判断不符合条件的
if (abs(root_bf) >= 2 || root_bf != root->_bf)
{
cout << "平衡因子异常:" << root->_kv.first << endl;
return false;
}
//循环递归
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
//结点个数
int _Size(Node* root)
{
return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;
}
//树的高度
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}三、总结
本章主要详细的描述了AVL树的插入过程中出现的所有情况,以及介绍了旋转这一思路,使用图文配合能让我们更加深入理解旋转的过程,以及插入的流程,这个AVL的树插入实现为我们后面学习红黑树的学习提供的底层的思路,红黑树的学习也离不开旋转这一步骤,关键是理解插入实现。当然这个AVL树其次重点就是平衡检测,这个利用计数来高度差并于平衡因子来比较判断是否平衡思路也值得我们学习,这里还有AVL树的删除,可以参考《殷⼈昆 数据结构:⽤⾯向对象⽅法与C++语言描述》。