神经网络基础

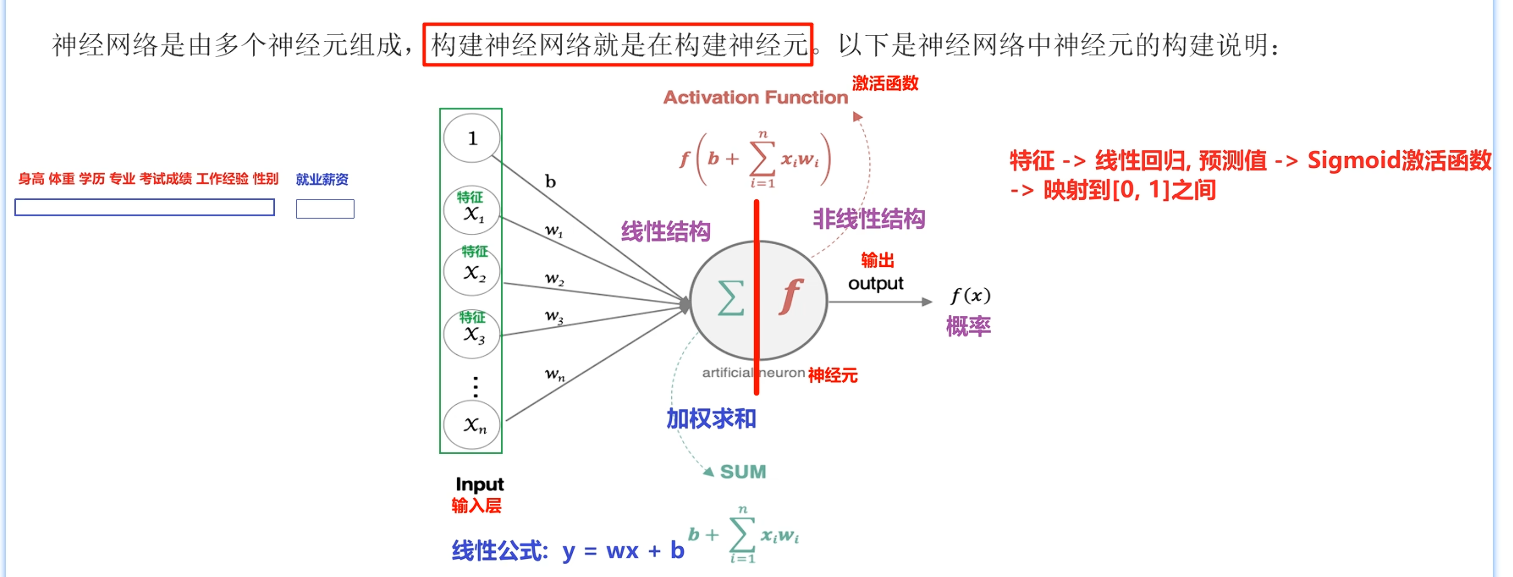
把输入层的特征进行加权求和，通过sigmod映射前面的加权求和结果

神经元死亡问题

如何选择激活函数:

复制代码

隐藏层:

    ReLU > Leaky ReLU > PReLU > Tanh > Sigmoid

输出层:

    二分类: Sigmoid + BCELoss 或 Softmax + CrossEntropyLoss（内部自动做 softmax）

    多分类: Softmax + CrossEntropyLoss（内部自动做 softmax）

    回归问题: identity(无需激活函数)，如果限制区间，则考虑ReLU, sigmoid, tanh

sigmoid激活函数

激活函数公式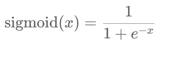：![](https://i-blog.csdnimg.cn/img_convert/bc813d1b6771b6d462196311ad0b5845.png)

激活函数求导公式：

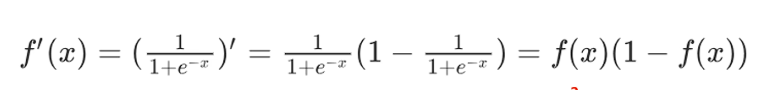
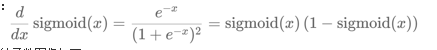
一般情况下sigmoid激活函数在五层之内就会出现梯度消失sigmoid函数一般只用于二分类的输出层

python 复制代码

import torch
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号


# 1. 创建画布和坐标轴, 1行2列.
fig, axes = plt.subplots(1, 2)

# 2. 生成 -20 ~ 20之间的 1000个数据点.
x = torch.linspace(-10, 10, 1000)
# print(f'x: {x}')

# 3. 计算上述1000个点, Sigmoid激活函数处理后的值.
y = torch.sigmoid(x)
# print(f'y: {y}')

# 4. 在第1个子图中绘制Sigmoid激活函数的图像.
axes[0].plot(x, y)
axes[0].set_title('Sigmoid激活函数图像')
axes[0].grid()

# 5. 在第2个图上, 绘制Sigmoid激活函数的导数图像.
# 5.1 重新生成 -20 ~ 20之间的 1000个数据点.
# 参1: 起始值, 参2: 结束值, 参3: 元素的个数, 参4: 是否需要求导.
x = torch.linspace(-20, 20, 1000, requires_grad=True)

# 5.2 具体的计算上述1000个点, Sigmoid激活函数导数后的值.
torch.sigmoid(x).sum().backward()

# 5.3 绘制图像.
axes[1].plot(x.detach(), x.grad)
axes[1].set_title('Sigmoid激活函数导数图像')
axes[1].grid(True)
plt.show()

tanh激活函数

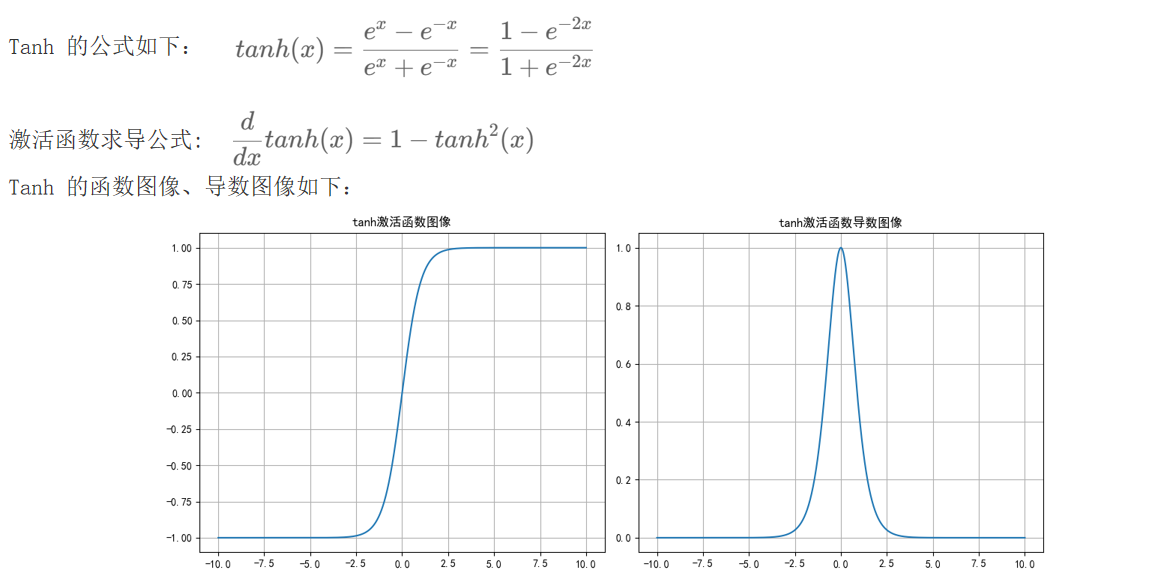
x越大整体越接近于1 x越小整体越接近于-1

tanh激活函数是将输入映射到[-1，1]之间

tanh是最优解的情况下是1

relu则永远是1

用于隐藏层，浅层网络(不超过5层)，存在梯度消失问题.输出范围(-1,1), 导数范围(0,1], 输入的有效区间[-3,3].

python 复制代码

import torch
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 微软雅黑
plt.rcParams['axes.unicode_minus'] = False            # 解决负号显示问题
# 1. 创建画布和坐标轴, 1行2列.
fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# 2. 生成 -10 ~ 10之间的 1000个数据点.
x = torch.linspace(-10, 10, 1000)

# 3. 上述1000个点, 输入tanh(x)
y = torch.tanh(x)

# 4. 在第1个子图中绘制tanh激活函数的图像.
axes[0].plot(x, y)
axes[0].set_title('tanh激活函数图像')
axes[0].grid()

# 5. 在第2个图上, 绘制tanh激活函数的导数图像.
# 重新生成 -10 ~ 10之间的 1000个数据点.
# 参1: 起始值, 参2: 结束值, 参3: 元素的个数, 参4: 是否需要求导.
x = torch.linspace(-10, 10, 1000, requires_grad=True)

# 上述1000个点, 输入tanh进行求导，sum().backward()
torch.tanh(x).sum().backward()

# 绘制图像
axes[1].plot(x.detach(), x.grad)
axes[1].set_title('tanh激活函数导数图像')
axes[1].grid()
plt.tight_layout()
plt.show()

Relu激活函数

复制代码

常用于 隐藏层，目前使用最多.

计算公式是max(0,x),输出范围[0,+∞]，导数0或1，计算简单，模型训练收敛快.

负数输入的输出为0，会带来稀疏性，起到正则化效果，利于图像类任务.

负数输入的梯度为0，可能导致部分神经元永久失活(dead ReLU)，是缺点，可以用 Leaky ReLU, PReLU 来考虑 负数输入的梯度.

python 复制代码

import  torch
import numpy as np

import matplotlib.pyplot as plt

import  matplotlib
matplotlib.use('TKAgg')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

#设置设备
device=torch.device('cuda' if torch.cuda.is_available() else 'cpu')

fig,axes=plt.subplots(1,2,figsize=(10,5))
#生成x轴的数据点 1000点 -10到10之间
x=torch.linspace(-10,10,1000)
#经过relu激活函数运算
y=torch.relu(x)
#4.在第一个子图上绘制relu激活函数图像

axes[0].plot(x,y)
axes[0].set_title('relu激活函数图像')
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
axes[0].grid()
#5.绘制relu激活函数的导数图像
#创建一个新的开启梯度计算的x
x=torch.linspace(-10,10,1000,requires_grad=True)
#经过relu激活函数运算 再求和
y=torch.relu(x).sum()
#反向传播,获取梯度值x.grad
y.backward()
axes[1].plot(x.detach(),x.grad)
axes[1].set_title('relu激活函数导数图像')
axes[1].set_xlabel('x')
axes[1].set_ylabel('y')
axes[1].grid()
plt.show()

softMAx激活函数

用于多分类任务的输出层，二分类任务上可以替代sigmoid.

输出各个类别的概率分布，范围(0,1), 并且概率总和为1.

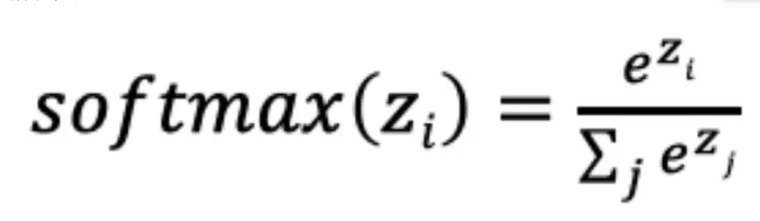
python 复制代码

import torch
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TKAgg')

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

#设置设备
device=torch.device('cuda' if torch.cuda.is_available() else 'cpu')

fig,axes=plt.subplots(1,2,figsize=(10,5))
#生成x轴的数据点 1000点 -10到10之间
x=torch.tensor([0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75])
#经过softmax激活函数运算
y=torch.softmax(x,dim=0)
#4.在第一个子图上绘制softmax激活函数图像

axes[0].bar(range(len(x)),y)
axes[0].set_title('softmax激活函数图像')
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
axes[0].grid()
#5.绘制softmax激活函数的导数图像
#创建一个新的开启梯度计算的x
z=torch.softmax(y,dim=0)
axes[1].bar(range(len(x)),z)

axes[1].set_title('softmax(softmax(x)')
axes[1].set_xlabel('x')
axes[1].set_ylabel('y')
axes[1].grid()
plt.show()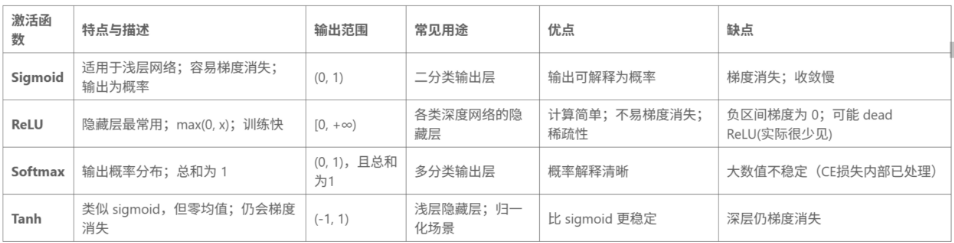

参数的初始化（仅了解）

因为后续的神经网络训练时默认都进行初始化

python 复制代码

案例：
    演示 参数初始化 的 7种方式
参数初始化的作用：
    1. 防止 梯度消失 或 梯度爆炸
    2. 提高收敛速度
    3. 打破对称性
参数初始化的方式：
    1. 均匀分布初始化  init.uniform
    2. 正态分布初始化  init.normal
    3. 全0初始化       init.zeros_
    4. 全1初始化       init.ones_
    5. 固定值初始化    init.constant
    6. kaiming 初始化，也叫做 HE 初始化
        正态分布的he初始化  init.kaiming_normal_
        均匀分布的he初始化  init.kaiming_uniform_
    7.xavier 初始化，也叫做 Glorot初始化
        正态化的Xavier初始化   init.xavier_normal_
        均匀分布的Xavier初始化  init.xavier_uniform_

总结:
    1.掌握 kaiming(权重w), xavier(权重w), 全0初始化(偏置)
    2.如何选择参数初始化方式：
        ReLU及其变体：kaiming
        非ReLU: xavier
        浅层：均匀分布初始化/正态分布初始化

python 复制代码

# 1. 均匀分布初始化
def demo01():
    print("1. 均匀分布初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 对权重w 进行初始化
    nn.init.uniform_(linear.weight)
    # 对偏置b 进行初始化
    nn.init.uniform_(linear.bias)
    # 打印
    print(linear.weight.data)
    print(linear.bias.data)
    print("-"*60)

python 复制代码

# 2. 正态分布初始化
def demo02():
    print("2. 正态分布初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 对权重w 进行初始化
    nn.init.normal_(linear.weight)
    # 对偏置b 进行初始化
    nn.init.normal_(linear.bias)
    # 打印
    print(linear.weight.data)
    print(linear.bias.data)
    print("-"*60)

python 复制代码

# 3. 全0初始化
def demo03():
    print("3. 全0初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 对权重w 进行初始化
    nn.init.zeros_(linear.weight)
    # 对偏置b 进行初始化
    nn.init.zeros_(linear.bias)
    # 打印
    print(linear.weight.data)
    print(linear.bias.data)
    print("-"*60)

python 复制代码

# 4. 全1初始化
def demo04():
    print("4. 全1初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 对权重w 进行初始化
    nn.init.ones_(linear.weight)
    # 对偏置b 进行初始化
    nn.init.ones_(linear.bias)
    # 打印
    print(linear.weight.data)
    print(linear.bias.data)
    print("-"*60)

python 复制代码

# 5. 固定值初始化
def demo05():
    print("5. 固定值初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 对权重w 进行初始化
    nn.init.constant_(linear.weight, 6)
    # 对偏置b 进行初始化
    nn.init.constant_(linear.bias, 6)
    # 打印
    print(linear.weight.data)
    print(linear.bias.data)
    print("-"*60)

python 复制代码

# 6. kaiming 初始化，也叫做 HE 初始化
def demo06():
    print("6. kaiming 初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 正态分布的he初始化
    print("正态分布的he初始化")
    # 对权重w 进行初始化
    nn.init.kaiming_normal_(linear.weight)
    # 打印
    print(linear.weight.data)
    # 均匀分布的he初始化
    print("均匀分布的he初始化")
    # 对权重w 进行初始化
    nn.init.kaiming_uniform_(linear.weight)
    # 打印
    print(linear.weight.data)
    print("-"*60)

python 复制代码

def demo07():
    print("7.xavier 初始化")
    # 创建一个线性层，输入维度3，输出维度5
    linear = nn.Linear(3, 5)
    # 正态分布的xavier初始化
    print("正态分布的xavier初始化")
    # 对权重w 进行初始化
    nn.init.xavier_normal_(linear.weight)
    # 打印
    print(linear.weight.data)
    # 均匀分布的xavier初始化
    print("均匀分布的xavier初始化")
    # 对权重w 进行初始化
    nn.init.xavier_uniform_(linear.weight)
    # 打印
    print(linear.weight.data)
    print("-"*60)