前言
今天接着和大家分享数据结构中栈相关的知识,特别是与java集合框架相关的内容,如果有了顺序表与链表的基础,接触今天分享的会是相当容易上手的,话不多说,让我们开始吧
一、java集合框架与Stack

- Java 集合框架是 Java 中用于存储和操作一组对象的体系,核心分为 Collection(单列集合)和Map(双列集合)
核心接口与分类
- Collection(单列集合)
- 是所有单列集合的根接口,定义了集合的基本操作(增删改查、遍历等)。
- 子接口:List(有序可重复)、Set(无序不可重复)、Queue(队列)。
- Map(双列集合)
- 存储键值对(Key-Value),Key 唯一、Value 可重复。
- 子接口:SortedMap(键有序)。
Stack
Stack 的继承关系(从提供的类图看)
从类图可知:
Stack 继承自 Vector(属于 List 分支),而Vector又继承自AbstractList、实现了List接口。
因此Stack本质是基于动态数组实现的,同时继承了Vector的线程安全特性(方法被synchronized修饰)。
Stack 的核心特性
- LIFO(后进先出):
- 新元素从 "栈顶" 加入,取出元素也只能从栈顶操作(最后加入的元素最先被取出)。
- 动态扩容:
底层基于Vector的动态数组,容量不足时会自动扩容(默认扩容为原容量的 2 倍)。 - 线程安全:
由于继承自Vector,Stack的方法(如push、pop)都被synchronized修饰,多线程环境下不会出现并发问题,但性能较低。
二、啥是栈
从数据结构 的角度来说,栈(Stack) 是一种遵循 后进先出(Last In First Out,简称 LIFO) 原则的线性数据结构 ,只允许在一端 进行元素的插入和删除操作,这个操作端被称为栈顶 ,另一端则被称为栈底。
- 就是说栈就是一种线性的数据结构,比如数组,链表.后面会具体说一下这两个的实现形式.
- 其中是满足先进后出的原则,大家可以想象一下手枪弹夹装弹的场景.
核心概念
- 栈顶(Top)
栈的操作端,所有的插入(入栈)、删除(出栈)、查看操作都只能在这一端进行。 - 栈底(Bottom)
栈的固定端,元素从栈顶入栈后,会依次向栈底方向排列,栈底元素是最先入栈且最后出栈的元素。 - 空栈
没有任何元素的栈,此时进行出栈或查看栈顶操作通常会触发异常。
核心操作
栈的操作非常简洁,只有两个核心基础操作,以及两个常用辅助操作:
| 操作名称 | 功能描述 | 注意事项 |
|---|---|---|
| 入栈(Push) | 将元素添加到栈顶 | 若栈已满(顺序栈),会触发"栈溢出" |
| 出栈(Pop) | 移除并返回栈顶元素 | 若栈为空,会触发"下溢"异常 |
| 查看栈顶(Peek/Top) | 返回栈顶元素,但不移除 | 若栈为空,触发异常 |
| 判空(IsEmpty) | 判断栈中是否有元素 | 无 |
说明:栈不支持在中间位置插入、删除或访问元素,这是它区别于数组、链表等线性结构的关键特征。
栈的两种实现方式
从数据结构的底层存储来看,栈有两种常见实现方式:
-
顺序栈(基于数组实现)
- 原理 :用一段连续的内存空间(数组)存储栈元素,用一个变量标记栈顶的位置(如
top指针,初始值为-1表示空栈)。 - 入栈 :
top指针加 1,将元素存入数组对应下标位置。 - 出栈 :返回数组
top下标对应的元素,top指针减 1。 - 优缺点:访问速度快,但存在固定容量限制,满栈后扩容需要额外开销。
- 典型例子 :Java 中遗留的
Stack类、ArrayDeque类。
- 原理 :用一段连续的内存空间(数组)存储栈元素,用一个变量标记栈顶的位置(如
-
链式栈(基于链表实现)
- 原理 :用链表存储栈元素,一般选用带头结点的单链表,栈顶对应链表的头结点之后的第一个节点(避免复杂的尾操作)。
- 入栈:将新节点插入到链表头部(栈顶)。
- 出栈:删除链表头部的节点,返回其值。
- 优缺点:容量可以动态增长,不存在溢出问题,但每个元素需要额外存储指针,空间开销略大。
- 典型例子:自定义链式栈结构。
三、常用代码手动实现(数组类型实现)
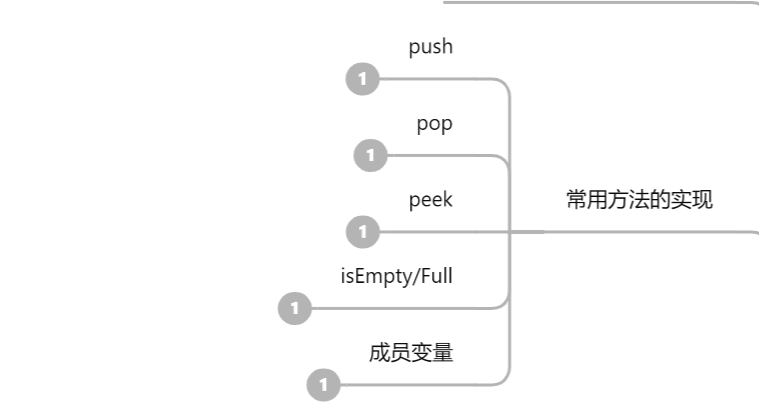
- 这一部分的逻辑是较为简单的,小伙伴们如果是第一次接触,非常建议大家上手实现一下~
我就都分成一个一个小的代码块了 大家在学习的时候也可以分成基本成员变量 ,成员方法,**辅助方法(在成员方法中被调用的小方法)**进行学习
基本方法
java
public class MyStack<E> {
public Object[] elem ;
//标记最后一个
public int usedSize;
public static final int DEFAULT_CAPACITY = 5;
public MyStack(){
this.elem = new Object[DEFAULT_CAPACITY];
}
//入栈方法
public void push(E val){
if (isFull()){
elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize] = val;
usedSize ++;
}
public boolean isFull(){
return usedSize == DEFAULT_CAPACITY;
}
public E pop(){
if(isEmpty()){
return null;
}
E ret = (E)elem[usedSize-1];
usedSize--;
return ret;
}
public boolean isEmpty(){
return usedSize == 0;
}
public E peek(){
if(isEmpty()){
return null;
}
return (E)elem[usedSize-1];
}四、逆波兰表达式
逆波兰表达式 (Reverse Polish Notation,简称 RPN),也叫后缀表达式 ,是一种不需要括号来标识运算优先级的算术表达式表示方法。
它的核心特点是:运算符位于其对应的所有操作数之后 。
与之相对的,我们日常使用的 3 + 4、(2 + 3) × 5 这类表达式叫中缀表达式------运算符位于两个操作数中间。
- 中缀转后缀
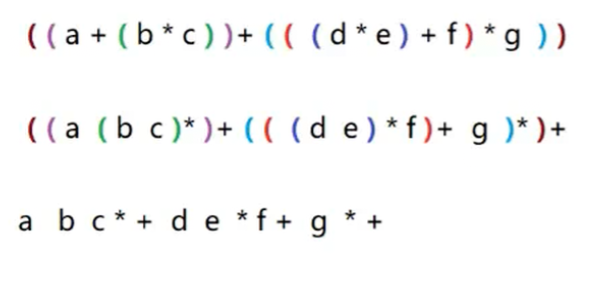
一、 中缀表达式 vs 逆波兰表达式
通过表格可以更直观地理解两者的转换关系:
| 中缀表达式 | 逆波兰表达式 | 计算逻辑 |
|---|---|---|
3 + 4 |
3 4 + |
先取 3 和 4,再执行加法 |
(2 + 3) × 5 |
2 3 + 5 × |
先算 2+3,结果再和 5 相乘 |
3 + 4 × 2 |
3 4 2 × + |
先算 4×2,结果再和 3 相加 |
(3 + 4) × (5 - 2) |
3 4 + 5 2 - × |
先算 3+4 和 5-2,再将两个结果相乘 |
二、 逆波兰表达式的计算规则
逆波兰表达式的计算非常适合用栈来实现,步骤如下:
- 从左到右扫描表达式中的每个元素(数字或运算符)。
- 遇到数字:直接压入栈中。
- 遇到运算符 :从栈中弹出两个元素 (注意顺序:先弹出的是右操作数 ,后弹出的是左操作数),用该运算符对两个数进行计算,再将计算结果压入栈中。
- 扫描结束后,栈中剩余的唯一元素就是表达式的最终结果。
四、 逆波兰表达式的优势
- 无需括号:完全通过运算符的位置来体现运算优先级,没有歧义。
- 计算高效 :用栈实现的计算过程时间复杂度为 O(n)O(n)O(n),逻辑简单,适合计算机处理。
- 编译器常用:很多编译器在处理算术表达式时,会先将中缀表达式转为逆波兰表达式,再进行计算,避免了复杂的括号和优先级判断。
五、根据逆波兰表达式求值
java
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String x: tokens){
//判断是运算符号还是数值
if(!isOperations(x)){
//不是运算符
stack.push(Integer.parseInt(x)) ;
}else {
//是运算符
int right = stack.pop();
int left = stack.pop();
//直到具体的操作符
switch (x){
case "+" :
stack.push(left + right);
break;
case "-" :
stack.push(left - right);
break;
case "*" :
stack.push(left * right);
break;
case "/" :
stack.push(left / right);
break;
}
}
}
return stack.pop();
}
public boolean isOperations(String x){
if (x.equals("+") || x.equals("-") ||
x.equals("*") || x.equals("/") ){
return true;
}
return false;
}五、 总结
-
虽然栈的方法不是很多,但是栈这种独特的思想在编程题目中有着不少的应用,大家可以找两个感受感受~
-
到这里我的分享就先结束了~,希望对你有帮助
-
我是dylan 下次见~
- 无限进步