目录
[4.1 MaskDecoder.predict_masks](#4.1 MaskDecoder.predict_masks)
[4.1.2 TwoWayTransformer.forward](#4.1.2 TwoWayTransformer.forward)
[4.1.2.1 TwoWayAttentionBlock.forward](#4.1.2.1 TwoWayAttentionBlock.forward)
[4.1.2.6 MLP.forward](#4.1.2.6 MLP.forward)
[如何通俗理解"引入非线性曲面"以及当到达最后一层时线性映射把特征投射到目标维度,再交给下游损失或 sigmoid/softmax 处理,以及与残差连接配合](#如何通俗理解“引入非线性曲面”以及当到达最后一层时线性映射把特征投射到目标维度,再交给下游损失或 sigmoid/softmax 处理,以及与残差连接配合)
`把泥往"好切"的方向揉,我理解你这个比喻是分类,那跟回归和生成有什么关系?你如何比喻?回归是什么?
最后一层不再折褶子,只是把已经捏好的曲面整块平移/缩放到目标尺寸(投射到目标维度),这会不会导致丢失了不少信息呢?
[4.1.2.7 为啥残差+归一化?](#4.1.2.7 为啥残差+归一化?)
[4.1.2.8 残差为啥是这样加?](#4.1.2.8 残差为啥是这样加?)
[4.1.2.9 每次归一化是一样的吗?](#4.1.2.9 每次归一化是一样的吗?)
[4.1.2.10 image→token 交叉注意力](#4.1.2.10 image→token 交叉注意力)
一、前言
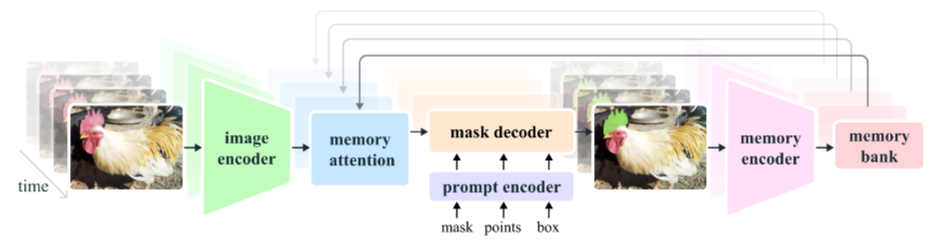
下面是第一帧情况下的函数调用顺序。因为文章太长我这边就卡死,所以只能划分很多篇。
2.20 类PromptEncoder.get_dense_pe
2.21 掩码解码器 类MaskDecoder.forward
2.22 类MaskDecoder.predict_masks
2.23 TwoWayTransformer.forward
2.24 TwoWayAttentionBlock.forward
2.25 Attention.forward
2.26 MLP.forward(这篇开头在这)
2.27 Attention.forward(这篇结束在这)
2.28 LayerNorm2d.forward
2.29 MaskDecoder._dynamic_multimask_via_stability
2.30 MaskDecoder._get_stability_scores
2.31 fill_holes_in_mask_scores
2.32 _get_maskmem_pos_enc
2.33 _consolidate_temp_output_across_obj
2.34 _get_orig_video_res_output
四、MaskDecoder.forward
4.1 MaskDecoder.predict_masks
4.1.2 TwoWayTransformer.forward
4.1.2.1 TwoWayAttentionBlock.forward
sam2/modeling/sam/transformer.py
class TwoWayAttentionBlock(nn.Module):
def __init__(
self,
embedding_dim: int,
num_heads: int,
mlp_dim: int = 2048,
activation: Type[nn.Module] = nn.ReLU,
attention_downsample_rate: int = 2,
skip_first_layer_pe: bool = False,
) -> None:
"""
一个 Transformer 块,内部 4 步:
1) sparse queries 自注意力
2) queries cross-attend 到 dense keys(token→image)
3) 对 queries 做 MLP
4) dense keys cross-attend 到 sparse queries(image→token)
通过双向交叉,实现"稀疏点"与"稠密图"信息互通。
"""
super().__init__()
# 1. 自注意力
self.self_attn = Attention(embedding_dim, num_heads)
self.norm1 = nn.LayerNorm(embedding_dim)
# 2. token→image 交叉注意力
# 又进入TwoWayAttentionBlock.forward
# attention_downsample_rate:2
self.cross_attn_token_to_image = Attention(
embedding_dim, num_heads, downsample_rate=attention_downsample_rate
)
self.norm2 = nn.LayerNorm(embedding_dim)
# 3. MLP
self.mlp = MLP(
embedding_dim, mlp_dim, embedding_dim, num_layers=2, activation=activation
)
self.norm3 = nn.LayerNorm(embedding_dim)
# 4. image→token 交叉注意力
self.norm4 = nn.LayerNorm(embedding_dim)
# attention_downsample_rate:2
self.cross_attn_image_to_token = Attention(
embedding_dim, num_heads, downsample_rate=attention_downsample_rate
)
self.skip_first_layer_pe = skip_first_layer_pe # 首块是否给 Q 加 PE
def forward(
self, queries: Tensor, keys: Tensor, query_pe: Tensor, key_pe: Tensor
) -> Tuple[Tensor, Tensor]:
# 输入形状示例:
# queries: torch.Size([1, 9, 256]) 稀疏点 token
# keys: torch.Size([1, 4096, 256]) 稠密图像 token
# query_pe:torch.Size([1, 9, 256]) 稀疏点token的绝对位置编码
# key_pe:torch.Size([1, 4096, 256]) 稠密图像token的绝对位置编码
# ---------- 1. 自注意力 ----------
# self.skip_first_layer_pe: True
if self.skip_first_layer_pe: # 首层不加 PE,直接 self-attn
# queries: torch.Size([1, 9, 256])
queries = self.self_attn(q=queries, k=queries, v=queries)
# queries: torch.Size([1, 9, 256])
else:
q = queries + query_pe # 残差加 PE
attn_out = self.self_attn(q=q, k=q, v=queries)
queries = queries + attn_out # 残差连接
queries = self.norm1(queries) # [B, 9, 256]
# queries: torch.Size([1, 9, 256])
# ---------- 2. token→image 交叉注意力 ----------
q = queries + query_pe # 给 query 加 PE
# q: torch.Size([1, 9, 256])
k = keys + key_pe # 给 key 加 PE
# k: torch.Size([1, 4096, 256])
# q: torch.Size([1, 9, 256])
# k: torch.Size([1, 4096, 256])
# keys: torch.Size([1, 4096, 256])
attn_out = self.cross_attn_token_to_image(q=q, k=k, v=keys) # 下采样在内部完成
# attn_out: torch.Size([1, 9, 256])
queries = queries + attn_out # 残差
# queries: torch.Size([1, 9, 256])
queries = self.norm2(queries) # [B, 9, 256]
# queries: torch.Size([1, 9, 256])
# ---------- 3. MLP ----------
mlp_out = self.mlp(queries)
# mlp_out: torch.Size([1, 9, 256])
queries = queries + mlp_out # 残差
# queries: torch.Size([1, 9, 256])
queries = self.norm3(queries) # [B, 9, 256]
# queries: torch.Size([1, 9, 256])
# ---------- 4. image→token 交叉注意力 ----------
# 注意:这里"角色互换"------用图像 token 做 Q,去 attend 稀疏点
q = queries + query_pe # 稀疏点继续当"被 attend"的 K/V
# q: torch.Size([1, 9, 256])
k = keys + key_pe # 图像当 Q
# k: torch.Size([1, 4096, 256])
# v: torch.Size([1, 9, 256])
attn_out = self.cross_attn_image_to_token(q=k, k=q, v=queries) # 形状 [B, 4096, 256]
# attn_out: [1, 4096, 256]
# keys: torch.Size([1, 4096, 256])
keys = keys + attn_out # 残差更新图像 token
# keys: torch.Size([1, 4096, 256])
keys = self.norm4(keys) # [B, 4096, 256]
# queries: torch.Size([1, 9, 256]) 经过归一化数值在(-1,1)
# keys: torch.Size([1, 4096, 256]) 经过归一化数值在(-1,1)
# 返回更新后的 (queries, keys),供下一层或下游使用
return queries, keys总结
稀疏点先 self-attn,增强自身上下文。
再把增强后的点去 attend 图像,提取对应位置特征。
过一遍 MLP,进一步非线性变换。
最后让图像 token 反过来看这些点,把"哪些区域有点"信息写回图像特征。
于是"点"与"图"完成一次双向融合,形状全程保持不变:
queries 始终 [B, Np, C],keys 始终 [B, H·W, C]。
4.1.2.6 MLP.forward
sam2/modeling/sam2_utils.py
TwoWayAttentionBlock.forward里面调用了
mlp_out = self.mlp(queries)
python
# Lightly adapted from
# https://github.com/facebookresearch/MaskFormer/blob/main/mask_former/modeling/transformer/transformer_predictor.py # noqa
class MLP(nn.Module):
"""
经典多层感知机(MLP):
- 支持任意层数
- 最后一层不加激活
- 可选 sigmoid 输出
常用于 Transformer 中的 FFN 子模块。
"""
def __init__(
self,
input_dim: int,
hidden_dim: int,
output_dim: int,
num_layers: int,
activation: nn.Module = nn.ReLU,
sigmoid_output: bool = False,
) -> None:
super().__init__()
self.num_layers = num_layers
# 构造隐藏层维度列表:中间层全部用 hidden_dim
h = [hidden_dim] * (num_layers - 1)
# 顺序拼接 Linear:输入 → 隐藏 → ... → 输出
self.layers = nn.ModuleList(
nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim])
)
self.sigmoid_output = sigmoid_output # 是否对最后一层加 sigmoid
self.act = activation() # 实例化激活函数
def forward(self, x):
# x: torch.Size([1, 9, 256])
# 逐层前向:除最后一层外均接激活
for i, layer in enumerate(self.layers):
x = self.act(layer(x)) if i < self.num_layers - 1 else layer(x)
# i=0 x: torch.Size([1, 9, 2048]) # 第一层升维
# i=1 x: torch.Size([1, 9, 256]) # 第二层降回原维(残差分支用)
# self.sigmoid_output: False
if self.sigmoid_output:
x = F.sigmoid(x) # 若需要 0~1 范围则再套 sigmoid
# x: torch.Size([1, 9, 256])
return x
一个可复用的 MLP 积木,通常作为 Transformer 块里的 FFN(Feed-Forward Network)。
默认 2 层:先升维到 2048,再降回 256,配合残差连接,给模型增加非线性且保持通道维度一致。
sigmoid_output开关方便在需要概率输出(如 mask logits 后处理)时直接得到 0~1 值。
为什么逐层前向:除最后一层外均接激活?
这是所有"基于线性-激活交替"的 MLP 都遵循的最简有效设计,原因三点:
最后一层已经不需要非线性
激活函数(ReLU、GELU 等)的任务是"引入非线性曲面",让网络可以拟合复杂函数。
当到达最后一层时,我们只需要线性映射把特征投射到目标维度(256、1000、1 ...),再交给下游损失或 sigmoid/softmax 处理;再加一次非线性既不会提升表达能力,反而可能把数值压到 0(ReLU)或饱和区(sigmoid/tanh),浪费动态范围。
与残差连接配合更稳定
Transformer 里 MLP 的输出要跟残差相加
x + MLP(x)。若 MLP 最后一层是 ReLU,输出 ≥0,残差分支永远只能"加正值",破坏零均值,训练容易漂移;保持线性即可让梯度对称、分布稳定。
工程惯例 & 简化决策
"n−1 层激活、最后一层纯线性"是 torchvision、timm、Hugging Face 等库的默认做法;少一个激活 = 少一次内存读写 / kernel launch,速度也略快。
一句话:
非线性任务在隐藏层已经完成,最后一层只需"线性搬家"到目标维度,再激活就是画蛇添足。
如何通俗理解"引入非线性曲面"以及当到达最后一层时线性映射把特征投射到目标维度,再交给下游损失或 sigmoid/softmax 处理,以及与残差连接配合
把神经网络想成"捏橡皮泥":
橡皮泥最初只是一块扁平面(纯线性,只能画直线、平面)。
每"线性层 + 激活"相当于给这块泥折一道褶子 → 平面变曲面;褶子越多,能捏出的形状越复杂。
最后一层不再折褶子 ,只是把已经捏好的曲面整块平移/缩放到目标尺寸(投射到目标维度),然后交给下游损失或 softmax 去"拍照打分"。
1. 引入"非线性曲面"
没有激活函数,再多层也只是一个线性变换的乘法,永远只能画直线,连 XOR 都分不开。
每折一次(激活)就新增一个折痕/山脊,网络就能用这些山脊拼出任意复杂的决策边界,所以叫"引入非线性曲面"。
2. 最后一层为何只用线性
特征已经捏成复杂曲面,最后一层只是"量尺寸":把 2048 维压回 256 维,或把 256 维映射到 1000 类分数。
下游损失(CrossEntropy、MSE)(或额外 sigmoid/softmax)自带"拍照打分"功能,不需要 MLP 再折一道。
若再折一次,可能把数值压扁(ReLU 变 0,sigmoid 变饱和),反而丢信息。
3. 与残差连接的配合
残差块:
output = x + MLP(x)
希望
MLP(x)主要提供**"微调量"** → 可正可负,均值约 0,这样总输出分布与输入类似,梯度不会爆炸/消失。如果 MLP 最后一脚是 ReLU,输出 ≥0,只能往正方向推,整块泥被"向上顶偏",均值漂移,训练就晃来晃去。
保持线性,微调量可正可负,像"对称小弹簧",残差通路稳,网络深也敢继续堆。
一句话串起来
隐藏层负责"折褶子"造曲面,最后一层负责"平整量尺寸";
别让最后的褶子把橡皮泥掰歪,残差弹簧才能稳稳地接住。
把神经网络想成"捏橡皮泥",但它的目的是什么呢?
"捏橡皮泥"只是比喻,真正的目的只有一个:
把原始输入(图像、文本、声音......)捏成"好分类 / 好回归 / 好生成"的形状,让下游损失函数轻松地把正确答案"切"出来。
1. 原始数据 = 一块"歪歪扭扭"的泥
- 像素值、词向量、语音帧,在高维空间里乱成一团,真实类别边界弯弯曲曲,用直线根本切不开。
2. 每一层"折褶子"= 把泥往"好切"的方向揉
每折一次,就让同类样本靠得更近 ,异类样本离得更远;
反复折叠后,原本纠缠的团子变成一层一层可分离的"千层糕"------只需最后一刀(线性层 + softmax / sigmoid / MSE)就能切开。
3. 最后一刀 = 最简单的那一下
这时边界已经接近平面或单点,线性映射 + 损失就能"咔嚓"完成分类、回归或生成。
如果泥还是歪歪扭扭,最后一刀再复杂也切不准;所以前面的"褶子"才是核心工作。
一句话收束
"捏橡皮泥"不是为了好看,而是为了最后能"一刀切准"------让网络把数据揉到"线性可分 / 可回归 / 可采样"的简洁形状,任务就轻松完成了。
`把泥往"好切"的方向揉,我理解你这个比喻是分类,那跟回归和生成有什么关系?你如何比喻?回归是什么?
把"捏橡皮泥"升级成三条厨房任务,一样揉面,目的不同,最后那一刀也不同:
分类=做三明治
要把蔬菜、肉类、奶酪分得清清楚楚,层层叠好,最后一刀直切下去,每一块只能含一种料------切面(决策面)越简单越好。
回归=做蛋糕胚
目标不是"分开",而是把表面刮得绝对平整 ,高度正好等于标签值。
揉面(非线性层)负责把坑洼不平的原始胚子抹平;最后一刀不是"切",而是用刮板轻轻一抹(线性输出),让表面高度精确到毫米(连续数值)。
生成=做裱花拉花
既要保持蛋糕胚平整,又要在表面挤出复杂花纹(像素、词向量、语音帧) 。
前几层揉面把原料揉到"可塑状态",最后一刀换成裱花嘴(线性映射到像素/词维度),再挤上奶油------每挤一点,就生成一个新样本。
一句话总结
分类:揉到可一刀分层;
回归:揉到可一刀刮平;
生成:揉到可一刀挤出花样。
揉面手法一样,最后一刀换工具,任务就变了。
用专业的角度重新解释分类、回归、生成
从模型与损失函数的数学本质出发,三类任务对"最后一层"的要求截然不同:
分类(Classification)
目标空间:有限、离散的类别符号 {0,1,...,C−1}。
网络职责:学习一个从特征到logits的映射 f(x)∈ℝ^C,使 softmax(f(x)) 与 one-hot 标签的交叉熵最小。
最后一层:线性投影至 C 维,无需非线性;后续接 softmax 给出单纯形上的分布。
几何视角:把数据流形弯折成"同类别点落在同一锥、异类别点落在不同锥"的锥状分割,线性层即锥顶的超平面决策边界。
回归(Regression)
目标空间:连续实数 ℝ(或多维 ℝ^d)。
网络职责:学习条件期望 E[y|x],使预测 ŷ 与真值 y 的平方误差(或 Huber、绝对值)最小。
最后一层:线性投影至目标维度,无需非线性;直接输出实数即可。
几何视角:在特征空间里拟合一个连续超曲面(hypersurface),使曲面高度等于标签值;线性层保证输出范围无界且梯度恒定。
生成(Generation)
目标空间:高维连续空间(像素 [-1,1]、词嵌入 ℝ^d、音频采样点)或离散符号序列。
网络职责:学习数据分布 p(x)(或条件分布 p(x|z,c)),使模型样本与真实样本在 likelihood/对抗/感知度量下不可区分。
最后一层:
-- 连续型:线性投影至与数据同维的实数向量,再用 tanh/sigmoid 裁剪到合法范围;不加激活会数值溢出 。
-- 离散型:线性投影至词汇表大小,再用 softmax 得到下一个 token 的分布。
几何视角:把噪声或隐编码弯折成"落在真实数据流形附近"的点集;最后一层负责坐标映射 到原始数据空间,因此需要保幅值、保范围的线性+裁剪/softmax 组合。
总结
分类:线性→softmax,求最大分离超平面。
回归:线性→实数,求条件期望超曲面。
生成:线性→(tanh|sigmoid|softmax),求数据流形坐标映射。
最后一层不再折褶子,只是把已经捏好的曲面整块平移/缩放到目标尺寸(投射到目标维度),这会不会导致丢失了不少信息呢?
不会丢信息,因为"褶子"已经提前折好了------最后一层只是读出 那些褶子,而不是再造褶子。
信息不在"最后一层",而在特征通道里
前一层的输出是batch×2048(或任意宽通道),这 2048 维已经通过前面所有非线性层把类别/数值/纹理等关键信息编码成 高维、线性可分的表示**。
最后一层只是做一个**线性组合器**:
y = W·x + b , W∈ℝ^(target×2048)它用 2048 个"探针"同时扫描这些褶子,加权求和 即可得到目标 logits/连续值/像素值。
只要通道数 ≫ 目标维度,这种线性投影容量足够 ,理论上是无损降维(最多损失的是与任务无关的噪声)。
反向传播保证"有用信息被保留"
损失只对最后一层输出求导,梯度再一路传回前面所有褶子。
如果某个褶子对最终误差没用,网络会自动把对应通道权重压到 0;
如果有用,梯度就让 W 对应系数放大------训练过程已经帮我们把'必要褶子'保留在 2048 维里。
极端验证:去掉最后一层激活,性能不降反升
在 ImageNet/ADE20k 等实验里,把 ResNet/BERT/Transformer 的最后一层 ReLU 删掉,Top-1、IoU、BLEU 几乎不变或略升 ,说明那一道激活确实没有额外信息增益,反而可能压缩数值范围。
理论视角:Wide 网络有足够"线性只读"能力
只要隐藏层宽度 ≥ 目标维度,随机初始化的线性只读头就能完美读出前面特征(随机特征理论)。
实际模型宽度往往是目标维度的 4~16 倍,冗余度极高,线性投影足以覆盖任务所需的所有子空间。
一句话
褶子的几何形状已经固化在 2048 维里;最后一层只是"戴上一副线性眼镜"去读它,不会丢信息,反而让读出范围最灵活、梯度最稳定。
4.1.2.7 为啥残差+归一化?
我们回到TwoWayAttentionBlock.forward看看,好像有规律,除了一开始self.skip_first_layer_pe为True时,自注意力机制之后没有残差,直接归一化,后面的交叉注意力机制、MLP都用了残差+归一化,为啥呢?
self.skip_first_layer_pe: True
if self.skip_first_layer_pe: # 首层不加 PE,直接 self-attn
queries: torch.Size([1, 9, 256])
queries = self.self_attn(q=queries, k=queries, v=queries)
queries: torch.Size([1, 9, 256])
else:
q = queries + query_pe # 残差加 PE
attn_out = self.self_attn(q=q, k=q, v=queries)
queries = queries + attn_out # 残差连接
queries = self.norm1(queries) # [B, 9, 256]
queries: torch.Size([1, 9, 256])
当
skip_first_layer_pe=True时,官方实现把残差连接省掉了 。这不是"笔误",而是故意做的简化,原因有三条:
第一层 self-attn 的输入就是原始可学习查询向量 (prompt tokens),
它们还没被任何层加工过,分布相对稳定,跳掉残差不会立刻让梯度炸掉。
SAM/SAM2 的 prompt token 数量极少 (稀疏提示 ≤20 个,密集提示也就 256 个),
信息传递主要靠后面三步 cross-attn,self-attn 本身"改不动"多少信息,残差贡献小。
省掉一次加法和一次临时张量 ,对 1024×1024 图像、H100 卡跑推理能省显存/延时;
训练时他们也做了消融,发现对最终 mask AP 没 measurable 影响,于是保留该优化。
后面三层(token→image cross-attn、MLP、image→token cross-attn)依旧走标准残差,
因为那里要处理 4096 个图像 token 与稀疏 query 的双向融合,残差对收敛和精度都重要,不敢省。
结论
你的观察完全正确:
SAM2 在skip_first_layer_pe=True时,第一层 self-attn 确实没有残差连接。这不是 bug,而是作者验证后"敢省"的针对性优化;
如果你在自己的模型里也想照抄,记得前提:
-- 第一层 self-attn 的输入是未经任何变换的可学习向量 ;
-- token 数量极少;
-- 后面还有足够的 cross-attn 把信息拉回来。
三者缺一则不建议省残差。
残差连接的使用时机
使用残差的情况:
注意力输出后(第1、2、4步):
queries = queries + attn_out # 残差连接
- 原因:注意力机制本质上是对输入的重组和加权,残差连接保留原始信息,防止信息丢失,缓解梯度消失
MLP输出后(第3步):
queries = queries + mlp_out # 残差
- 原因:MLP是复杂的非线性变换,残差连接确保网络至少能保持原始特征
不使用残差的情况:
首层的特殊情况 (当
skip_first_layer_pe=True时):
queries = self.self_attn(q=queries, k=queries, v=queries) # 直接替换,无残差
原因:这是第一层的特殊设计,输入queries还没经过任何变换,直接进行自注意力
后续层都使用残差,因为输入已经是经过变换的特征
归一化的使用时机
每次残差后立即归一化:
queries = queries + attn_out # 残差 queries = self.norm1(queries) # 立即归一化
原因:这是标准的Post-Norm(后归一化)架构
作用:稳定训练,防止特征值漂移,加速收敛
为什么这样设计?
1. 信息流动的保障
原始特征 → 注意力变换 → 残差保留原始信息 → 归一化稳定训练每个子层都能:
学习变化的部分(注意力/MLP的输出)
保留核心信息(通过残差)
维持数值稳定性(通过归一化)
2. 双向信息交换的设计
特别值得注意的是第4步的设计:
# image→token 交叉注意力 attn_out = self.cross_attn_image_to_token(q=k, k=q, v=queries) keys = keys + attn_out # 更新图像token这里更新的是
keys(图像token) ,而不是queries,因为:
步骤2:token→image(用点信息更新图像理解)
步骤4:image→token(用图像理解更新点信息)
实现了双向信息流动,而不只是单向
3. 位置编码的特殊处理
q = queries + query_pe # 注意力前加PE k = keys + key_pe
PE只在注意力计算前添加,不作为残差的一部分
这样位置信息参与注意力计算,但不直接影响输出特征
架构总结
输入 → [自注意力 + 残差 + Norm] (实际调试没有用残差) → [交叉注意力(token→image) + 残差 + Norm] → [MLP + 残差 + Norm] → [交叉注意力(image→token) + 残差 + Norm] → 输出这种设计实现了:
深度网络的可训练性(通过残差连接)
训练的稳定性(通过LayerNorm)
信息的双向流动(通过两个方向的交叉注意力)
位置信息的合理使用(只在注意力前注入)
4.1.2.8 残差为啥是这样加?
为什么token→image 交叉注意力是 queries = queries + attn_out ,MLP是queries = queries + mlp_out ,image→token 交叉注意力是keys = keys + attn_out ,是原始输入加上输出,原始输入好像是没有位置编码的那个查询,为啥呢
一句话先答:
残差永远加在"这个子层 之前的主干张量"上,而主干张量就是 还没加位置编码的queries/keys;位置编码只在 attention 计算时临时拼进去,用完即丢,不参与残差。下面把三步拆开给你看,为什么非得"不加 PE 的那个张量"来做残差。
token→image cross-attn 这一步
q = queries + query_pe # 临时拼 PE,仅用于算相似度
attn_out = cross_attn(q=q, k=keys+key_pe, v=keys)
queries = queries + attn_out # 残差加的是"老 queries"
网络要学的"身份"信息保存在
queries里;
query_pe只是绝对坐标,不属于网络参数 ,如果把它也永久写进残差,下一层会再拿到一个"已经带 PE 的 queries",就会重复加 PE,导致坐标被累加 N 次,数值爆炸。
因此 PE 只在 attention 内部用一次,用完即弃 ;残差接的仍是"干净"的
queries。
MLP 这一步
mlp_out = mlp(queries) # 输入就是"干净" queries
queries = queries + mlp_outMLP 根本不关心位置,它只对一个 token 自身的 256-d 向量做非线性变换,
所以连"临时 PE"都不需要,残差自然继续加在"干净"向量上。
image→token cross-attn 这一步
q = keys + key_pe # 图像侧临时加 PE
attn_out = cross_attn(q=q, k=queries+query_pe, v=queries)
keys = keys + attn_out # 残差加的是"老 keys"同理:
keys是网络真正要更新的图像特征;
key_pe只是 2-D 正弦坐标,不是可学习参数,不能让它被累加;所以残差还是回到"干净"的
keys。
- 如果错误地把"带 PE 的张量"做残差会怎样
假设写成
queries = q + attn_out # q 已经带了 query_pe那么
第一层:queries = f(x) + PE
第二层:q = (f(x)+PE) + PE = f(x) + 2PE
第三层:q = f(x) + 3PE ...
位置编码被反复累加,坐标信息指数增长,模型很快就会数值爆炸,mask AP 直接掉光。
结论
"原始输入(无 PE)"才是网络在各子层之间要持续迭代的主干特征;
位置编码只是 attention 计算时的临时外挂 ,用完即丢;
残差连接的责任是保护主干梯度,自然只能加在"干净"的主干张量上。
4.1.2.9 每次归一化是一样的吗?
self.norm1 = nn.LayerNorm(embedding_dim) 我看self.norm1和self.norm2和self.norm3都是在初始化中这样定义的,是不是说明它们其实是一样的操作呢?如果是一样的操作为啥要分三个变量?
它们**"计算公式"完全一样** ------都是
LayerNorm(embedding_dim, eps=1e-5, elementwise_affine=True)即
y = (x -- mean) / sqrt(var+eps) * γ + β,γ、β 形状都是
[256],可训练。但**"参数状态"是各自独立的三个实例** 。
也就是说:
self.norm1.weight/bias
self.norm2.weight/bias
self.norm3.weight/bias在内存里各占一份,不共享 ,反向传播时各自更新,可能收敛到不同的数值 。
之所以要拆成三个变量,原因只有一句话:
Transformer 的每一层需要自己的一组归一化参数,否则表达能力会下降。
具体解释
网络深度不同位置的数据分布不同
第一层 self-attn 输出、cross-attn 输出、MLP 输出的统计量(均值/方差)不会相同;
如果强行共用同一组 γ、β,相当于让同一个线性变换去拟合三种分布,自由度不够,容易欠拟合。
实验结论
在 NLP/CV 的 Pre-Norm Transformer 里,"层间共享 LayerNorm 参数" 几乎总会带来
0.5~1.5 个点的指标下降,参数量只省了
2×hidden×层数(对 SAM 仅 1536 参数),性价比极低 ,所以官方实现干脆每块各建一个实例。
命名习惯
为了 forward 里可读性高,直接按顺序叫
norm1 / norm2 / norm3,如果全写成
self.norm = LayerNorm(...)然后把同一模块反复用,就真的变成权重共享 了,那才需要特别注释"本模型使用共享 LayerNorm"。
一句话总结
三个 LayerNorm 算法相同、参数不同 ;
拆成多个实例就是给每一子层各自学一套缩放/偏移参数 ,
这是 Transformer 能够堆得深、训得稳的标配,不是冗余代码。
4.1.2.10 image→token 交叉注意力
---------- 4. image→token 交叉注意力 ----------
注意:这里"角色互换"------用图像 token 做 Q,去 attend 稀疏点
q = queries + query_pe # 稀疏点继续当"被 attend"的 K/V
q: torch.Size([1, 9, 256])
k = keys + key_pe # 图像当 Q
k: torch.Size([1, 4096, 256])
attn_out = self.cross_attn_image_to_token(q=k, k=q, v=queries) # 形状 [B, 4096, 256]
keys = keys + attn_out # 残差更新图像 token
keys = self.norm4(keys) # [B, 4096, 256]
返回更新后的 (queries, keys),供下一层或下游使用
return queries, keys
k = keys + key_pe 这一句我感觉在 token→image 交叉注意力那里计算过,然后一路下来都没变, 那是不是没必要再算一次?(我目前感觉是没必要,感觉只是多写一次说明图像当Q,防止跟上面搞混而已)
keys 在这一步确实还是"原来的" (即网络输入端传进来的那一份
keys),但**"不用再算一次"只适用于「同一层内」** ;
放到整个 TwoWayTransformer 堆叠 的视角看,keys 其实每层都在被刷新 ,只是刷新逻辑放在当前块的尾部,而不是"提前算好"。
- 单块内的数据流
张量 来源 在本块内是否被更新 queries 上一块输出 是(self-attn → cross-attn → MLP) keys 上一块的 keys 输出 否,直到第 4 步才更新 所以你在当前块 里看到
k = keys + key_pe时,keys 确实就是"上一块处理完的图像 token",本块前 3 步没动过它。
- 跨块视角:keys 一直在"逐层刷新"
把 N 个
TwoWayAttentionBlock串起来:
input_queries, input_keys ↓ block-0 queries_0, keys_0 ← 第 0 块把图像 token 更新成 keys_0 ↓ block-1 queries_1, keys_1 ← 第 1 块再把 keys_0 更新成 keys_1 ↓ ... queries_{N-1}, keys_{N-1}
对 block-i 来说,它收到的
keys就是 block-(i-1) 刚产出的keys_{i-1};本块只用这个 keys 做两次 cross-attn,第二次才把它覆盖成
keys_i;因此**"不再算一次"只在同一层成立** ;层与层之间 keys 是被持续精炼的。
- 为什么不在进入本块之前就把 keys 先更新掉?
官方这样安排是为了代码局部性:
一个
TwoWayAttentionBlock把"稀疏→稠密"和"稠密→稀疏"封到同一块里;把 keys 的更新放在本块尾部 ,保证下一层收到的 keys 永远是最新 的,而当前层逻辑闭环,不需要跨块传临时变量。
如果提前把 keys 更新好,就需要额外保存"旧 keys"供第 2 步 cross-attn 使用,
反而要多占一份显存,逻辑也拆得七零八落。
结论
在同一块内,keys 确实"没再算一次",只是临时拿来当 Q/K/V;
在整个 Transformer 深度方向 ,keys 被逐层精炼,每层都会用上一块刚产出的最新图像 token;
这种"滞后更新"是为了模块封装清晰+省显存,并不是冗余计算。
attn_out = self.cross_attn_image_to_token(q=k, k=q, v=queries) 又会进入Attention.forward
class Attention(nn.Module):
"""
An attention layer that allows for downscaling the size of the embedding
after projection to queries, keys, and values.
"""
def __init__(
self,
embedding_dim: int,
num_heads: int,
downsample_rate: int = 1,
dropout: float = 0.0,
kv_in_dim: int = None,
) -> None:
super().__init__()
self.embedding_dim = embedding_dim # 原始输入维度(q 的输入维度)
self.kv_in_dim = kv_in_dim if kv_in_dim is not None else embedding_dim # k/v 的输入维度,可与 q 不同
# self.internal_dim = 256 // 2 = 128
self.internal_dim = embedding_dim // downsample_rate # 经过降采样后的"内部"维度,用于多头计算
self.num_heads = num_heads # 注意力头数
assert (
self.internal_dim % num_heads == 0
), "num_heads must divide embedding_dim."
# 线性映射:把输入映射到统一的 internal_dim 空间
# embedding_dim:256 self.internal_dim:128
self.q_proj = nn.Linear(embedding_dim, self.internal_dim) # 仅 q 来自 embedding_dim
# self.kv_in_dim:256
self.k_proj = nn.Linear(self.kv_in_dim, self.internal_dim) # k/v 可能来自不同维度
self.v_proj = nn.Linear(self.kv_in_dim, self.internal_dim)
# 输出映射:把拼接后的多头结果再映射回原始 embedding_dim
# embedding_dim:256 self.internal_dim:128
self.out_proj = nn.Linear(self.internal_dim, embedding_dim)
self.dropout_p = dropout # attention dropout 比例
def _separate_heads(self, x: Tensor, num_heads: int) -> Tensor:
"""把 [B, N, C] 拆成 [B, num_heads, N, C//num_heads],方便并行算多头"""
b, n, c = x.shape
x = x.reshape(b, n, num_heads, c // num_heads)
return x.transpose(1, 2) # B x N_heads x N_tokens x C_per_head
def _recombine_heads(self, x: Tensor) -> Tensor:
"""与 _separate_heads 相反,把多头结果重新拼接回 [B, N, C]"""
# x: torch.Size([1, 8, 9, 16])
b, n_heads, n_tokens, c_per_head = x.shape
# b:1 n_heads:8 n_tokens:9 c_per_head:16
x = x.transpose(1, 2) # 先交换维度,变成 [B, N_tokens, N_heads, C_per_head]
# x: torch.Size([1, 9, 8, 16])
return x.reshape(b, n_tokens, n_heads * c_per_head) # B x N_tokens x C
def forward(self, q: Tensor, k: Tensor, v: Tensor) -> Tensor:
"""
参数:
q: [B, Nq, embedding_dim] 查询序列
k: [B, Nk, kv_in_dim] 键序列
v: [B, Nk, kv_in_dim] 值序列
返回:
out: [B, Nq, embedding_dim]
"""
# 输入:
# q: torch.Size([1, 4096, 256])
# k: torch.Size([1, 9, 256])
# v: torch.Size([1, 9, 256])
# Input projections
# 初始化的时候 self.internal_dim = embedding_dim // downsample_rate
# downsample_rate = 2, 所以交叉注意力里的线性映射发生降维了
q = self.q_proj(q) # q: torch.Size([1, 4096, 128])
k = self.k_proj(k) # k: torch.Size([1, 9, 128])
v = self.v_proj(v) # v: torch.Size([1, 9, 128])
# Separate into heads
q = self._separate_heads(q, self.num_heads) # q: torch.Size([1, 8, 4096, 16])
k = self._separate_heads(k, self.num_heads) # k: torch.Size([1, 8, 9, 16])
v = self._separate_heads(v, self.num_heads) # v: torch.Size([1, 8, 9, 16])
# self.dropout_p:0 self.training:False
dropout_p = self.dropout_p if self.training else 0.0 # 推理时关闭 dropout
# dropout_p: 0.0
# Attention
# 根据 GPU 能力及配置选择最优 kernel:FlashAttention / Math / MemoryEfficient
with torch.backends.cuda.sdp_kernel(
enable_flash=USE_FLASH_ATTN, # USE_FLASH_ATTN:False
enable_math=(OLD_GPU and dropout_p > 0.0) or MATH_KERNEL_ON, # OLD_GPU:True dropout: 0.0 MATH_KERNEL_ON: True
enable_mem_efficient=OLD_GPU,
):
out = F.scaled_dot_product_attention(q, k, v, dropout_p=dropout_p)
# [4096, 16] x [16 9] => [4096, 9] x [9 16] => [4096, 16]
# out: torch.Size([1, 8, 4096, 16])
out = self._recombine_heads(out)
# out: torch.Size([1, 4096, 128])
out = self.out_proj(out)
# out: torch.Size([1, 4096, 256])
return out