Day42：单调栈part2（42.接雨水、84.柱状图中最大的矩形）

42.接雨水

题目链接 ：https://leetcode.cn/problems/trapping-rain-water/description/

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

总结

1. 常规做法

我们不要一下子去算所有的水，试着只关注某一根 柱子（比如下标为 i 的位置）。

具体到每一根柱子 i，它上面能存多少水，取决于：

它左边所有柱子里最高的那个（记为 Lmax）。
它右边所有柱子里最高的那个（记为 Rmax）。
这两者中较矮的那个决定了水位的高度。

在这个基础上，我们需要减去柱子本身的高度，剩下的就是水深。

所以计算公式为：存水量 = min(Lmax, Rmax) - height[i]

我们可以构建一个完整的 left_max 数组。对于每一个位置 i，left_max[i] 就代表了它左边（包括它自己）最高的柱子。右边 right_max 同理。

java 复制代码

leftMax[i] = Math.max(height[i], leftMax[i - 1]);

rightMax[i] = Math.max(height[i], rightMax[i+1]);

到现在为止，我们的解题蓝图已经非常清晰了，就像盖房子一样分成了三步：

第一遍循环 ：从左往右，算出 leftMax 数组。
第二遍循环 ：从右往左，算出 rightMax 数组。
第三遍循环：遍历每个位置，计算并累加存水量。

代码如下：

java 复制代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] leftMax = new int[n];
        int[] rightMax = new int[n];

        // 记录每个柱子左边柱子最大高度
        leftMax[0] = height[0];
        for (int i = 1; i < n; i++) {
            leftMax[i] = Math.max(leftMax[i - 1], height[i]);
        }
        // 记录每个柱子右边柱子最大高度
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            rightMax[i] = Math.max(rightMax[i + 1], height[i]);
        }

        // 求和
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += Math.min(leftMax[i], rightMax[i]) - height[i];
        }

        return sum;
    }
}

2. 双指针优化（降低空间复杂度至O(1)）

（1）整体思路

Step 1: 宏观视角

想象雨水降落下来，一个位置能存水，前提是它形成了一个"坑"。这个坑的高度由左右两边的"墙"决定。对于任意位置 i，存水量 = min(LeftMax, RightMax) - height[i]。

Step 2: 动态维护最值

我们不需要预先计算所有位置的左右最高墙（那样需要 O(N) 的额外空间）。我们只需要两个指针 l 和 r，以及两个变量 maxLeft 和 maxRight 记录指针扫描过的区域的最高值。

Step 3: 贪心策略 (短板原理)

如果在某一时刻，左边的最高墙 maxLeft 小于右边的最高墙 maxRight。
这就意味着：对于左指针 l 来说，它的左边界限制 (maxLeft) 已经确定比右边的某堵墙要矮了。
无论 l 和 r 中间还有什么惊天动地的高墙，都不会影响 l 位置的存水量，因为水会从 maxLeft 这一侧流走（maxLeft 是瓶颈）。
结论：此时可以安全地结算左指针 l 的水量，并移动左指针。
反之亦然，如果右边较矮，就结算右指针 r 的水量。

Step 4: 结束条件

当 l 和 r 相遇并交错时，说明所有柱子都遍历完毕，累加的结果即为总量。

（2）核心：循环逻辑

java 复制代码

while (l <= r) {
    // 1. 更新当前位置左右两侧已知的最高墙
    maxLeft = Math.max(maxLeft, height[l]);
    maxRight = Math.max(maxRight, height[r]);

    // 2. 核心判断：决定结算哪一边的水
    if (maxLeft < maxRight) {
        res += maxLeft - height[l ++];
    } else {
        res += maxRight - height[r --];
    }
}

更新最值 ：每次循环开始，先尝试更新 maxLeft 和 maxRight。这意味着 maxLeft 始终代表 l 左侧（包含 l）最高的墙，maxRight 代表 r 右侧（包含 r）最高的墙。
短板决断 (if (maxLeft < maxRight))：这是算法的精髓。
- 对于位置 l 来说，它能装水的公式本应是： $\\min(\\text{左边最高}, \\text{右边最高}) - \\text{当前高度}$ 。
- 关键推导 ：如果我们发现 maxLeft < maxRight，虽然 maxRight 只是 r 右边的最大值，不是 l 右边全局的最大值 ，但因为 l 右边至少有一个 maxRight 挡着，且 maxLeft 已经比它小了，所以 maxLeft 一定是那个"短板"。
- 因此，我们不需要知道 l 右边确切的最高墙是谁，只要知道右边有一堵墙比左边高，就可以安全地计算 l 位置的水量了。
计算与移动：
- 如果左边是短板 (maxLeft < maxRight)：当前位置 l 的存水量 = maxLeft - height[l]。算完后 l 向右移。
- 如果右边是短板 (else)：当前位置 r 的存水量 = maxRight - height[r]。算完后 r 向左移。

（3）代码实现

java 复制代码

class Solution {
    public int trap(int[] height) {
        if (height.length <= 2) {
            return 0;
        }
        // 从两边向中间寻找最值
        int maxLeft = height[0], maxRight = height[height.length - 1];
        int l = 1, r = height.length - 2;
        int res = 0;
        while (l <= r) {
            // 不确定上一轮是左边移动还是右边移动，所以两边都需更新最值
            maxLeft = Math.max(maxLeft, height[l]);
            maxRight = Math.max(maxRight, height[r]);
            // 最值较小的一边所能装的水量已定，所以移动较小的一边。
            if (maxLeft < maxRight) {
                res += maxLeft - height[l ++];
            } else {
                res += maxRight - height[r --];
            }
        }
        return res;
    }}

3. 单调栈

核心思路：找"凹槽"

我们需要维护一个单调递减栈 （栈底大，栈顶小）。栈中存储的是下标（Index），而不是高度值。

入栈条件 ：如果当前柱子的高度 height[i] 小于等于 栈顶柱子的高度，说明我们正在从左向右"下坡"，还没形成凹槽，直接将下标 i 入栈。
出栈（计算）条件 ：如果当前柱子的高度 height[i] 大于栈顶柱子的高度，说明遇到了一个"右边界"，此时形成了一个凹槽（V字形或U字形结构）。
- 凹槽底部（bottom）：栈顶弹出的元素。
- 左边界（left）：弹出后，新的栈顶元素(即原来的次栈顶元素)。
- 右边界（right） ：当前的 i。

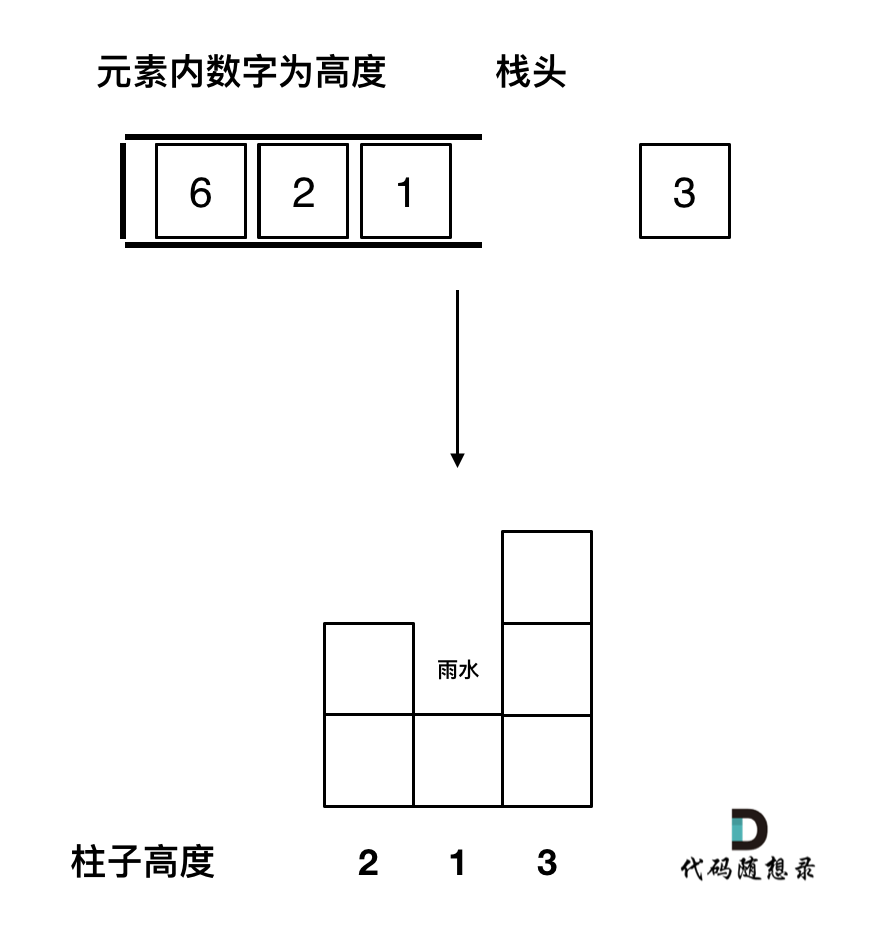
计算公式

当触发计算时（遇到更高的右边界）：

弹出栈顶元素作为坑底，记为 top。
如果栈变空了，说明只有右边界和底，没有左边界，兜不住水，直接 break。
获取新的栈顶元素作为左边界 ，记为 left。
计算雨水体积：
- 宽度 (w) = i - left - 1
- 高度 (h) = min(height[left], height[i]) - height[top]（左右墙较矮的那个减去坑底高度）
- 当前凹槽雨水 = w * h

代码实现

java 复制代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n <= 2) return 0; // 无法形成凹槽

        // 使用 Deque 作为栈，存储下标
        Deque<Integer> stack = new ArrayDeque<>();
        int ans = 0;

        for (int i = 0; i < n; i++) {
            // 当栈不为空，且当前高度大于栈顶高度时，说明形成了凹槽右侧
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                // 1. 取出凹槽底部（中间低的地方）
                int top = stack.pop();

                // 如果栈空了，说明没有左边界，存不住水
                if (stack.isEmpty()) {
                    break;
                }

                // 2. 获取左边界下标
                int left = stack.peek();

                // 3. 计算这一层的宽和高
                // 宽度是左右墙之间的距离
                int w = i - left - 1; 
                // 高度是左右墙较矮者减去坑底高度
                int h = Math.min(height[left], height[i]) - height[top];

                ans += w * h;
            }
            // 无论如何，当前位置都需要入栈（要么作为新墙，要么作为坑底）
            stack.push(i);
        }

        return ans;
    }
}

84.柱状图中最大的矩形

题目链接 ：https://leetcode.cn/problems/largest-rectangle-in-histogram/description/

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

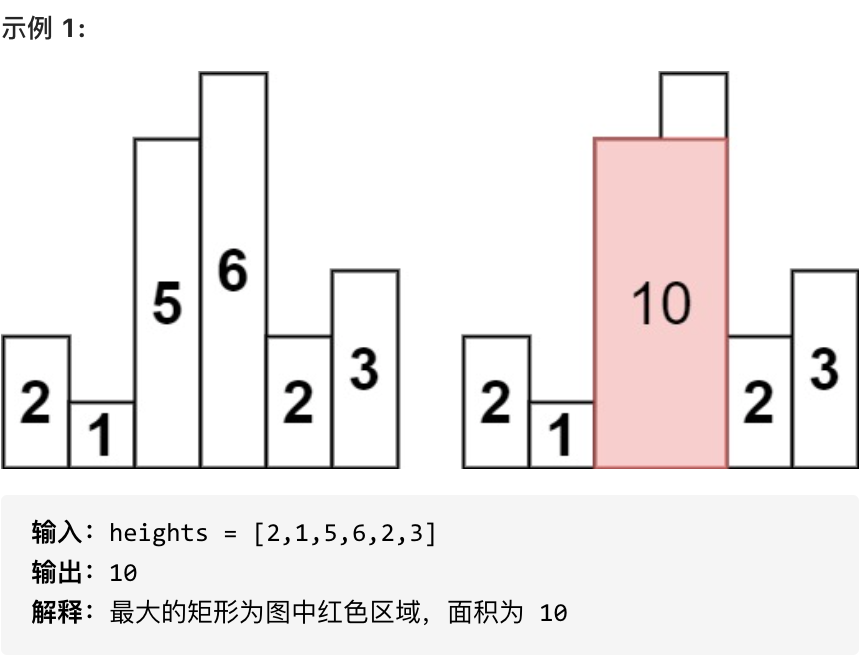
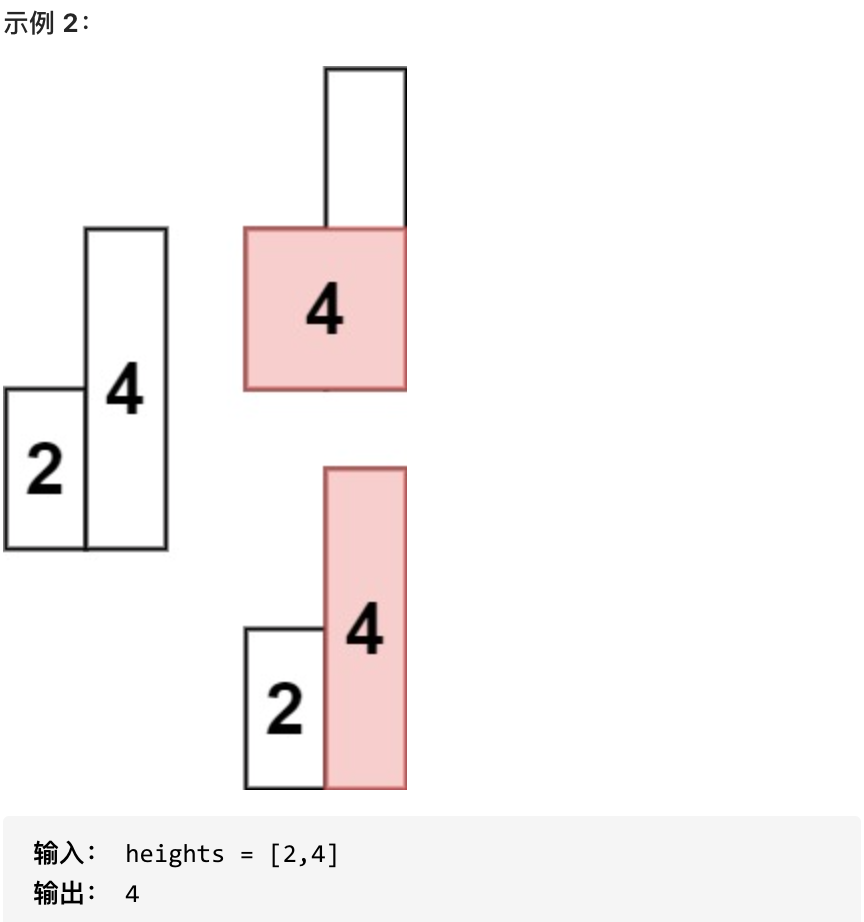
1 <= heights.length <=10^5
0 <= heights[i] <= 10^4

总结

1. 核心思路：以"高"定"宽"

要找到最大面积，我们可以转换一下思路：

对于数组中的每一个柱子，假设以该柱子的高度 h 作为矩形的高度，那么这个矩形最大能有多宽？

向左找 ：找到第一个高度小于 h 的柱子下标 left。
向右找 ：找到第一个高度小于 h 的柱子下标 right。
当前宽 ：width = right - left - 1
当前面积 ：area = h * width

示例解析 [2, 1, 5, 6, 2, 3]：

对于高度 5 (下标 2)：
- 向左看：下标 1 的高度是 1 (<5)，停下。
- 向右看：下标 4 的高度是 2 (<5)，停下。
- 宽度 = 4 - 1 - 1 = 2。
- 面积 = 5 * 2 = 10。
对于高度 6 (下标 3)：
- 左边是 5 (<6)，右边是 2 (<6)。
- 宽度 = 1，面积 = 6。

如果我们对每个柱子都暴力向两边扫描，时间复杂度是 O(N^2)，会超时。我们需要用单调栈一次遍历解决。

2. 单调栈解法详解

单调栈的作用是专门用来寻找"左边第一个比我小"和"右边第一个比我小"的元素。

在此题中，我们维护一个单调递增栈（栈底到栈顶，对应的柱子高度依次递增）。

算法流程：

哨兵技巧 ：为了处理方便（避免处理空栈或一直递增的情况），我们在原数组的头部和尾部各加一个高度为 0 的柱子。
遍历数组：
- 如果当前柱子高度 heights[i] 大于栈顶索引对应的柱子高度，直接入栈（因为还在递增，无法确定右边界）。
- 如果当前柱子高度 heights[i] 小于栈顶索引对应的柱子高度：
  - 说明栈顶那个柱子的右边界 确定了（就是当前 i）。
  - 弹出栈顶作为"中心柱子"来计算面积。
  - 弹出后，新的栈顶就是"中心柱子"的左边界。
  - 计算面积，更新最大值。
  - 重复此过程直到当前柱子不再小于栈顶高度，然后将当前 i 入栈。

3. 图解演示

输入：heights = [2, 1, 5, 6, 2, 3]

加哨兵后：tmp = [0, 2, 1, 5, 6, 2, 3, 0]

当前索引 i	高度 h[i]	栈操作 (存索引)	逻辑分析
0	0	`push 0`	栈: `[0]`
1	2	`push 1`	2 > 0 (递增)，入栈。栈: `[0, 1]`
2	1	1 < 2 (破坏递增)	计算! 栈顶是下标1(高度2)。右边界是i(2)，左边界是栈中下一个元素(0)。宽: `2-0-1=1`。面积: `2*1=2`。弹出1。栈: `[0]`。 1 > 0，入栈。栈: `[0, 2]`
3	5	`push 3`	5 > 1，入栈。栈: `[0, 2, 3]`
4	6	`push 4`	6 > 5，入栈。栈: `[0, 2, 3, 4]`
5	2	2 < 6 (破坏递增)	计算! 栈顶下标4(高6)。右边i(5)，左边3。宽 `5-3-1=1`，面积 `6`。弹出4。栈 `[0, 2, 3]`。 2 < 5 (继续) 计算! 栈顶下标3(高5)。右边i(5)，左边2。宽 `5-2-1=2`，面积 `5*2=10` (最大值!)。弹出3。栈 `[0, 2]`。 2 > 1，入栈。栈 `[0, 2, 5]`
...	...	...	后续同理...

4. Java 代码实现

java 复制代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        
        // 1. 创建新数组，首尾加 0 (哨兵)
        // 首位 0 防止栈空，末位 0 强迫所有元素最后出栈计算
        int[] newHeights = new int[n + 2];
        newHeights[0] = 0;
        System.arraycopy(heights, 0, newHeights, 1, n);
        newHeights[n + 1] = 0;
        
        // 2. 单调递增栈 (存储的是数组下标)
        Deque<Integer> stack = new ArrayDeque<>();
        int maxArea = 0;
        
        // 3. 遍历新数组
        for (int i = 0; i < newHeights.length; i++) {
            // 当当前高度 < 栈顶高度时，说明栈顶元素的右边界找到了
            while (!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]) {
                // 弹出栈顶，作为计算高度的柱子
                int curHeight = newHeights[stack.pop()];
                
                // 弹出后，新的栈顶就是 curHeight 的左边界
                int leftIndex = stack.peek();
                int rightIndex = i;
                
                // 计算宽度和面积
                int width = rightIndex - leftIndex - 1;
                maxArea = Math.max(maxArea, curHeight * width);
            }
            // 保持递增，入栈
            stack.push(i);
        }
        
        return maxArea;
    }
}

System.arraycopy 是 Java 中用于高效复制数组内容的一个本地方法（native method），它由 JVM 直接实现，性能优于手动循环复制。常用于数组拷贝、扩容、移动等操作。

java 复制代码

public static void arraycopy(
    Object src,      // 源数组
    int srcPos,      // 源数组起始位置（从0开始）
    Object dest,     // 目标数组
    int destPos,     // 目标数组起始位置
    int length       // 要复制的元素个数
);

java 复制代码

int[] src = {10, 20, 30, 40, 50};
int[] dest = {0, 0, 0, 0, 0, 0, 0};

System.arraycopy(src, 1, dest, 2, 3); // 从src[1]开始复制3个元素到dest[2]

// dest 变成 {0, 0, 20, 30, 40, 0, 0}

5. 与接雨水问题的区别

在接雨水问题中，需要在取完栈顶后判断是否为空，为什么这道题不需要？

java 复制代码

if (stack.isEmpty()) {
    break;
}

一句话回答： 在"接雨水"中，如果栈空了，说明左边没有墙 ，无法兜住水，所以要 break（放弃计算）；而在"最大矩形"的这个解法中，我们使用了哨兵（Sentinel）技巧 （首位加了 0），保证了栈永远不会为空，所以不需要判断。

即使不使用哨兵，"最大矩形"如果栈空了，意味着该柱子左边没有比它矮的，宽度可以直接延伸到最左侧，依然可以计算面积，而不是像接雨水那样放弃计算。

下面深入解析这两者的本质区别：

1. 代码层面的原因：哨兵 (Sentinel)

因为我们在数组最左边放了一个高度为 0 的柱子，并且先把它入栈了。而题目给定原本的 heights 都是非负整数（即 >=0）。

只要实际数据里有大于 0 的数，这个左哨兵 0 就永远处在栈底。
当 while 循环弹出元素时，弹到最后，栈里至少还会剩下一个 0（下标 0）。
因为 newHeights[i] 不可能小于 0（非负），所以栈底的这个 0 永远不会被 pop 出来。

结论：因为有左哨兵兜底，stack.isEmpty() 在 while 内部永远为 false，所以不需要判断。

2. 逻辑层面的本质区别（如果没有哨兵会怎样？）

假设我们不使用哨兵，直接处理原数组，两道题的处理逻辑也是完全不同的。

A. 接雨水 (Trapping Rain Water) ------ 需要"凹"字形

接雨水的核心逻辑是：找凹槽。

当前柱子是右墙。
弹出的栈顶是坑底。
新的栈顶是左墙。

逻辑链 ：如果不判断 isEmpty，当你弹出"坑底"后，发现栈空了，意味着没有左墙 。没有左墙，水会从左边流走，构不成"坑"。 所以必须 break，不能计算面积。

java 复制代码

// 接雨水逻辑
int bottom = stack.pop();
if (stack.isEmpty()) {
    break; // 没左墙，接不住水，退出
}
int leftWall = stack.peek(); // 获取左墙

B. 最大矩形 (Largest Rectangle) ------ 需要"凸"字形或阶梯

最大矩形的核心逻辑是：找边界。

当前柱子 i 是右边界（第一个比栈顶矮的）。
弹出的栈顶 h 是矩形高度。
新的栈顶是左边界 （栈顶元素下标 left）。

逻辑链 ：如果不使用哨兵，当你弹出 h 后，发现栈空了，这意味着什么？这意味着 h 左边没有任何比它矮的柱子 。既然左边都比 h 高（或者 h 就是第一个），那么这个矩形可以一直向左延伸到数组的起头（下标 -1）。

所以不需要 break，而是要特殊计算宽度：

复制代码

// 最大矩形（无哨兵版逻辑）
int h = heights[stack.pop()];
// 如果栈空了，说明左边没有比 h 矮的，宽度直接从 0 到 i
int width; 
if (stack.isEmpty()) {
    width = i; // 左边界视为 -1，宽度 = i - (-1) - 1 = i
} else {
    width = i - stack.peek() - 1;
}
maxArea = Math.max(maxArea, width * h);

3. 图解对比

我们可以通过下面的对比图更直观地理解这两种情况的差异：

接雨水 (No Left Wall)

复制代码

      |
      | (右墙 i)
      |
______|
 (坑底) 
Pop! -> Stack Empty
左边没墙，存不住水 -> Break

最大矩形 (No Left Boundary)

复制代码

      |
      |     |
      |     | (右边界 i)
______|_____|
  (高 h)
Pop! -> Stack Empty
左边没有比 h 矮的 -> 说明 h 可以一直延伸到最左边 -> 宽度 = i -> 继续计算