周志华《机器学习---西瓜书》七
七、贝叶斯理论
1. 贝叶斯决策论
概率框架下实施决策的基本理论
-
条件风险:给定NNN个类别,λij\lambda_{ij}λij是"将第jjj类误分为第iii类"的损失,将样本x\boldsymbol{x}x分到第iii类的条件风险为:
R(ci∣x)=∑j=1NλijP(cj∣x) R(c_i|\boldsymbol{x}) = \sum_{j=1}^N \lambda_{ij} P(c_j|\boldsymbol{x}) R(ci∣x)=j=1∑NλijP(cj∣x)
-
贝叶斯判定准则:选择风险最小的类别,即
h∗(x)=argminc∈YR(c∣x) h^*(\boldsymbol{x}) = \arg\min_{c\in\mathcal{Y}} R(c|\boldsymbol{x}) h∗(x)=argc∈YminR(c∣x)
-
核心概念:
- h∗(x)h^*(\boldsymbol{x})h∗(x)称为贝叶斯最优分类器 ,其总体风险为贝叶斯风险;
- 贝叶斯风险是学习性能的理论上限。
2. 判别式 vs. 生成式模型
-
背景:P(c∣x)P(c|\boldsymbol{x})P(c∣x)通常难以直接获得,机器学习通过两种策略估计后验概率。
-
判别式模型(Discriminative):
- 思路:直接对P(c∣x)P(c|\boldsymbol{x})P(c∣x)建模;
- 代表:决策树、BP神经网络、SVM。
-
生成式模型(Generative):
- 思路:先对联合概率分布P(x,c)P(\boldsymbol{x},c)P(x,c)建模,再通过P(c∣x)=P(x,c)P(x)P(c|\boldsymbol{x}) = \frac{P(\boldsymbol{x},c)}{P(\boldsymbol{x})}P(c∣x)=P(x)P(x,c)推导后验概率;
- 代表:贝叶斯分类器。
3. 贝叶斯定理
-
公式:
P(c∣x)=P(x,c)P(x)=P(c)P(x∣c)P(x) P(c|\boldsymbol{x}) = \frac{P(\boldsymbol{x},c)}{P(\boldsymbol{x})} = \frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})} P(c∣x)=P(x)P(x,c)=P(x)P(c)P(x∣c)
-
各部分含义:
- P(c)P(c)P(c):先验概率 (Prior),样本空间中类ccc的占比,可通过样本频率估计(大数定律);
- P(x∣c)P(\boldsymbol{x}|c)P(x∣c):样本相对于类标记的类条件概率(似然) ,样本x\boldsymbol{x}x属于类ccc的概率(估计难点);主要困难在于估计 似然 P(x∣c)P(\boldsymbol{x}|c)P(x∣c)
- P(x)P(\boldsymbol{x})P(x):证据 (Evidence)因子,与类别无关。
4. 极大似然估计
-
核心思路:先假设概率分布形式,再基于训练样例估计参数。
-
定义:假定P(x∣c)P(\boldsymbol{x}|c)P(x∣c)具有确定的概率分布形式,由参数θc\boldsymbol{\theta}_cθc唯一确定,则任务是利用训练集DDD中第ccc类样本集合DcD_cDc,θc\boldsymbol{\theta}_cθc的似然为:
P(Dc∣θc)=∏x∈DcP(x∣θc) P(D_c|\boldsymbol{\theta}c) = \prod{\boldsymbol{x}\in D_c} P(\boldsymbol{x}|\boldsymbol{\theta}_c) P(Dc∣θc)=x∈Dc∏P(x∣θc)
-
优化:连乘易下溢,因此通常改用对数似然:
LL(θc)=logP(Dc∣θc)=∑x∈DclogP(x∣θc) LL(\boldsymbol{\theta}_c) = \log P(D_c|\boldsymbol{\theta}c) = \sum{\boldsymbol{x}\in D_c} \log P(\boldsymbol{x}|\boldsymbol{\theta}_c) LL(θc)=logP(Dc∣θc)=x∈Dc∑logP(x∣θc)
-
极大似然估计变成: (频率主义提供的参数估计方法)
θ^c=argmaxθcLL(θc) \hat{\boldsymbol{\theta}}c = \arg\max{\boldsymbol{\theta}_c} LL(\boldsymbol{\theta}_c) θ^c=argθcmaxLL(θc)
5. 朴素贝叶斯分类器
-
核心问题:贝叶斯定理中P(x∣c)P(\boldsymbol{x}|c)P(x∣c) 所有属性上的联合概率难以从有限训练样本估计获得(组合爆炸、样本稀疏)。
-
基本思路:假定属性相互独立("朴素"的来源),因此联合概率可拆解为属性概率的乘积:
P(c∣x)=P(c)P(x∣c)P(x)=P(c)P(x)∏i=1dP(xi∣c) P(c|\boldsymbol{x}) = \frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})} = \frac{P(c)}{P(\boldsymbol{x})}\prod_{i=1}^d P(x_i|c) P(c∣x)=P(x)P(c)P(x∣c)=P(x)P(c)i=1∏dP(xi∣c)
(ddd为属性数,xix_ixi是x\boldsymbol{x}x在第iii个属性上的取值)
-
分类准则:因P(x)P(\boldsymbol{x})P(x)对所有类别相同,只需最大化分子,即
hnb(x)=argmaxc∈YP(c)∏i=1dP(xi∣c) h_{nb}(\boldsymbol{x}) = \arg\max_{c\in\mathcal{Y}} P(c)\prod_{i=1}^d P(x_i|c) hnb(x)=argc∈YmaxP(c)i=1∏dP(xi∣c)
朴素贝叶斯的概率估计方法
-
先验概率P(c)P(c)P(c)的估计:
P(c)=∣Dc∣∣D∣ P(c) = \frac{|D_c|}{|D|} P(c)=∣D∣∣Dc∣
(DcD_cDc是训练集DDD中类ccc的样本集合)
-
类条件概率P(xi∣c)P(x_i|c)P(xi∣c)的估计:
-
离散属性 :令Dc,xiD_{c,x_i}Dc,xi是DcD_cDc中第iii个属性取xix_ixi的样本集合,则
P(xi∣c)=∣Dc,xi∣∣Dc∣ P(x_i|c) = \frac{|D_{c,x_i}|}{|D_c|} P(xi∣c)=∣Dc∣∣Dc,xi∣
-
连续属性 :假设服从正态分布p(xi∣c)∼N(μc,i,σc,i2)p(x_i|c) \sim \mathcal{N}(\mu_{c,i}, \sigma^2_{c,i})p(xi∣c)∼N(μc,i,σc,i2),则概率密度为
p(xi∣c)=12πσc,iexp(−(xi−μc,i)22σc,i2) p(x_i|c) = \frac{1}{\sqrt{2\pi}\sigma_{c,i}} \exp\left(-\frac{(x_i - \mu_{c,i})^2}{2\sigma^2_{c,i}}\right) p(xi∣c)=2π σc,i1exp(−2σc,i2(xi−μc,i)2)
(μc,i\mu_{c,i}μc,i、σc,i\sigma_{c,i}σc,i是DcD_cDc中第iii个属性的均值、方差)
-
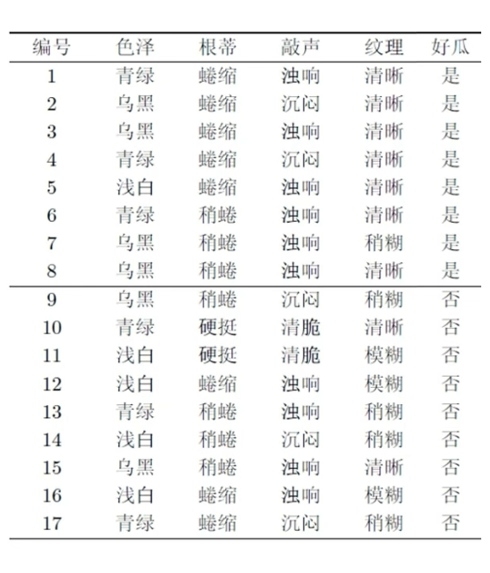
朴素贝叶斯示例(好瓜/坏瓜分类)
给定测试样本:(青绿;稍蜷;浊响;清晰),需判断是好瓜/坏瓜。
-
训练集统计(部分):
- 好瓜样本数∣Dyes∣=8|D_{yes}|=8∣Dyes∣=8,坏瓜∣Dno∣=9|D_{no}|=9∣Dno∣=9,总样本∣D∣=17|D|=17∣D∣=17;
- 好瓜下的属性概率:P(青绿∣yes)=3/8P(青绿|yes)=3/8P(青绿∣yes)=3/8、P(稍蜷∣yes)=3/8P(稍蜷|yes)=3/8P(稍蜷∣yes)=3/8、P(浊响∣yes)=6/8P(浊响|yes)=6/8P(浊响∣yes)=6/8、P(清晰∣yes)=7/8P(清晰|yes)=7/8P(清晰∣yes)=7/8;
- 坏瓜下的属性概率:P(青绿∣no)=3/9P(青绿|no)=3/9P(青绿∣no)=3/9、P(稍蜷∣no)=4/9P(稍蜷|no)=4/9P(稍蜷∣no)=4/9、P(浊响∣no)=4/9P(浊响|no)=4/9P(浊响∣no)=4/9、P(清晰∣no)=2/9P(清晰|no)=2/9P(清晰∣no)=2/9。
-
计算分子:
- 好瓜:P(yes)∏P(xi∣yes)=817×38×38×68×78P(yes)\prod P(x_i|yes) = \frac{8}{17} \times \frac{3}{8} \times \frac{3}{8} \times \frac{6}{8} \times \frac{7}{8}P(yes)∏P(xi∣yes)=178×83×83×86×87
- 坏瓜:P(no)∏P(xi∣no)=917×39×49×49×29P(no)\prod P(x_i|no) = \frac{9}{17} \times \frac{3}{9} \times \frac{4}{9} \times \frac{4}{9} \times \frac{2}{9}P(no)∏P(xi∣no)=179×93×94×94×92
-
结论:好瓜的分子更大,因此判定为"好瓜"。
6. 拉普拉斯修正
-
问题:若训练集中某属性值未与某类同时出现(如"敲声=清脆"的好瓜),会导致P(xi∣c)=0P(x_i|c)=0P(xi∣c)=0,进而使整个乘积为0("抹去"其他属性的信息)。
-
例如:若训练集中未出现"敲声=清脆"的好瓜,则模型在遇到"敲声=清脆"的测试样本时
-
修正方法:对概率估计加1平滑,公式为:
P^(c)=∣Dc∣+1∣D∣+N,P^(xi∣c)=∣Dc,xi∣+1∣Dc∣+Ni \hat{P}(c) = \frac{|D_c| + 1}{|D| + N}, \quad \hat{P}(x_i|c) = \frac{|D_{c,x_i}| + 1}{|D_c| + N_i} P^(c)=∣D∣+N∣Dc∣+1,P^(xi∣c)=∣Dc∣+Ni∣Dc,xi∣+1
(NNN是类别数,NiN_iNi是第iii个属性的取值数)
-
说明:引入了"属性值与类别均匀分布"的假设,会带来一定偏差,但避免了概率为0的问题。假设了属性值与类别的均匀分布,这是额外引入的bias
