先把"游戏规则"全部定死(非常重要)
1️⃣ 模型
y = wx +b
2️⃣ 数据(只用 1 个点)
x = 2 y_true = 4 3️⃣ 初始参数
w = 1 b = 0 4️⃣ Loss(平方误差)
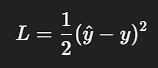
5️⃣ 学习率
lr = 0.1 二、前向传播(算预测)
1️⃣ 算预测值
y_hat = w x + b = 1 * 2 + 0 = 2 2️⃣ 算 loss
L = 1/2 * (2 - 4)^2 = 1/2 * 4 = 2 三、反向传播:算梯度(最关键)
我们现在问一个问题:
如果我把 w 稍微变大一点点,loss 是变大还是变小?
1️⃣ 写出 loss 关于 w 的公式
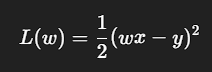
2️⃣ 对 w 求导(一步一步)
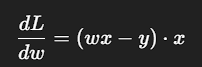
3️⃣ 代入当前数值
(w x - y) = (1 * 2 - 4) = -2
x = 2 所以代入公式2:
grad = -2 * 2 = -4 🔥 解释这个「-4」是什么意思
-
梯度是 负的
-
意味着:
👉 增大 w,会让 loss 下降
四、SGD 更新(你问的核心)
更新公式
w_new = w - lr * grad 代入数值
w_new = 1 - 0.1 * (-4) = 1 + 0.4 = 1.4 五、更新之后,loss 真的变小了吗?(验证)
新预测
y_hat = 1.4 * 2 = 2.8 新 loss
L = 1/2 * (2.8 - 4)^2 = 1/2 * 1.44 = 0.72 2 → 0.72,loss 真的下降了
六、再走一步
第二步更新
当前参数
w = 1.4 算梯度
(w x - y) = (1.4 * 2 - 4) = -1.2
grad = (w x - y) *x = -1.2 * 2 = -2.4 更新
w_new = 1.4 - 0.1 * (-2.4) = 1.64 loss
L = 1/2 * (1.64 * 2 - 4)^2 = 0.13 七、现在应该能"看见"梯度下降在干嘛了
梯度的 符号:告诉你往哪边走
梯度的 大小:告诉你走多远
学习率:控制步子大小
八、权重更新三步走:
1. 计算损失 - 前向传播
loss = criterion(model(inputs), labels) # 计算预测值与真实值的差异
2. 计算梯度 - 反向传播
loss.backward() # 自动计算所有参数的梯度并存储
3. 更新权重 - 优化器步进
optimizer.step() # 根据梯度更新模型参数