一.概述
在之前写过的一篇文章(【神经网络】超参调优策略(一):权重初始值调优------防止梯度消失和表现力受限)中,我们通过调整各层权重初始值使得各层的激活值分布会有适当的广度,从而可以顺利地进行学习,但当神经网络的层数、神经元数达到一定数量级时,如何确定最佳初始值成为一个难题,那么有没有那种可以强制性地调整激活值的分布,使其具备一定的广度呢?
有的,兄弟有的,这就是Batch Normalization算法。
二.Batch Normalization
Batch Normalization,顾名思义,以进行学习时的mini-batch为单位,按mini-batch进行使数据分布的均值为0、方差为1 的正规化,Batch Normalization具备以下优点:
- 减少学习时间,加快学习效率
- 对初始值不太敏感(初始值调优困难者狂喜)
- 可以抑制过拟合,降低Dropout的必要性
在设计神经网络时,Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此要向神经网络中插入对数据分布进行正规化的层,即BatchNormalization 层(下文简称Batch Norm层)
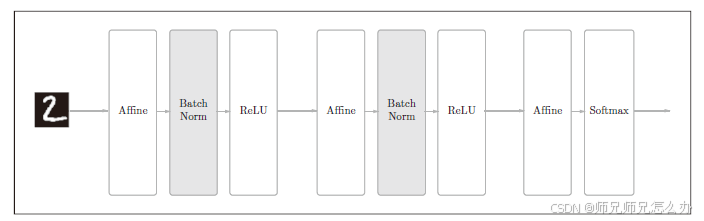
实现的公式也比较简单,首先是求均值和求方差,对mini-batch 的m个输入数据的集合B = {x1, x2, . . . , xm} 求均值和方差
:
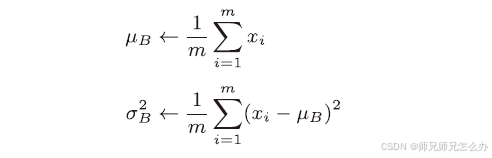
三.方差
均值就不说了,小学的知识,这里普及一下什么方差,方差是统计学中衡量数据离散程度(波动大小)的核心概念。其计算公式根据计算的是总体方差还是样本方差有所不同:
总体方差:计算 整个研究对象总体 中每个数据点与总体均值偏离程度的平方的平均值:
样本方差:当只有总体的一个样本时,用样本方差来估计总体方差。为了得到总体方差的无偏估计,分母使用 m - 1 (自由度),而不是样本大小 m:
其中:分母 m-1 是统计学中的一个关键点(称为贝塞尔校正)。使用 m-1 而不是 m 是为了修正样本均值 x̄ 本身也是从样本数据估计出来的这一事实,从而使得 成为总体方差
的无偏估计量。
其中: 为总体中第 i 个数据点
为总体均值,即上面的
m为总体的数据总个数
下面通过一个例子说明总体误差和样本误差:
假设我们有一组 5 个学生的数学考试成绩(满分 100 分):[85, 90, 78, 92, 80]
使用总体方差的第一步: 计算均值(μ)
第二步:计算每个数据点与均值的偏差
| 分数(xi) | 偏差(xi - μ) |
|---|---|
| 85 | 0 |
| 90 | +5 |
| 78 | -7 |
| 92 | +7 |
| 80 | -5 |
第三步:计算偏差的平方
| 偏差(xi - μ) | 平方((xi - μ)²) |
|---|---|
| 0 | 0 |
| +5 | 25 |
| -7 | 49 |
| +7 | 49 |
| -5 | 25 |
第四步:求和并除以数据个数(N=5)
分数与均值的平均偏离平方为 29.6 分,说明成绩波动较大(如 78 分和 92 分与均值差距明显),若方差为 0,则所有数据相同(无离散性)。
如果使用样本方差,则可以理解为 从更大班级中抽取的样本,则样本方差为:
在绝大多数实际应用中(如科学研究、市场调查、数据分析),你使用的是样本方差 (s²) ,因为你很少能掌握整个总体的数据。
四.正规化
对数据进行均值和方差之后,再对输入数据进行正规化,正规化(Standardization)是一种数据预处理方法,通过将数据转换为均值为0、标准差为(接近)1的标准正态分布 ,消除不同特征间的量纲差异。在机器学习中,标准化通常用于消除特征之间的量级差异,避免某些特征因数值较大而主导模型学习,从而加速收敛并提高泛化能力,公式为:
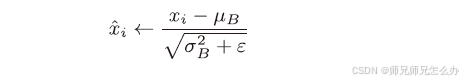
其中ε 是一个微小值(比如,10e-7之类的),它是为了防止出现除以0 的情况。接着,Batch Norm层会对正规化后的数据进行缩放和平移的变换:
其中r 和β 是参数。一开始r = 1,β = 0,然后再通过学习调整到合适的值。
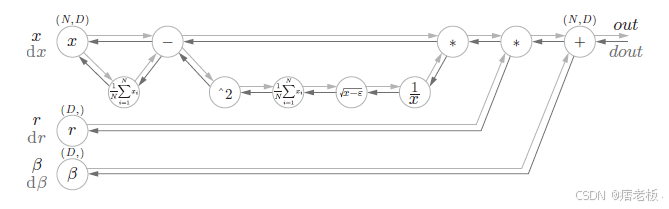
补充:所以整个正规化的正向推导公式为:
所以其正向推导可以转换成以下图示:
五.正规化转换后为何均值为0、标准差接近1?
- **均值为0的公式推导如下:**
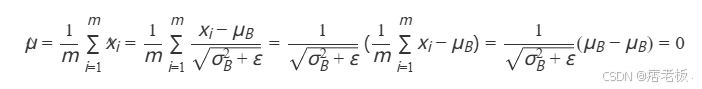
所以数据均值恒为0
- 标准差接近1的公式推导如下:

**3.举个例子:**假设原始数据 x=[1,3,5,7,9],则:
- 计算均值:
- 计算方差:
- 标准化后数据:
- 新数据均值:
- 新数据标准差:
标准化后的值表示原始数据偏离均值的"标准差倍数",如上述例子中-1.414表示比均值低4.414个标准差,可用于不同单位的数据(如厘米、千克)的直接比较。
六.代码实现
最后我们通过之前编写的文章(XXX)中使用的一个例子MINI数据集来观察不使用Batch Normalization和使用了Batch Normalization时给予不同的初始值尺度,观察学习的过程如何变化:
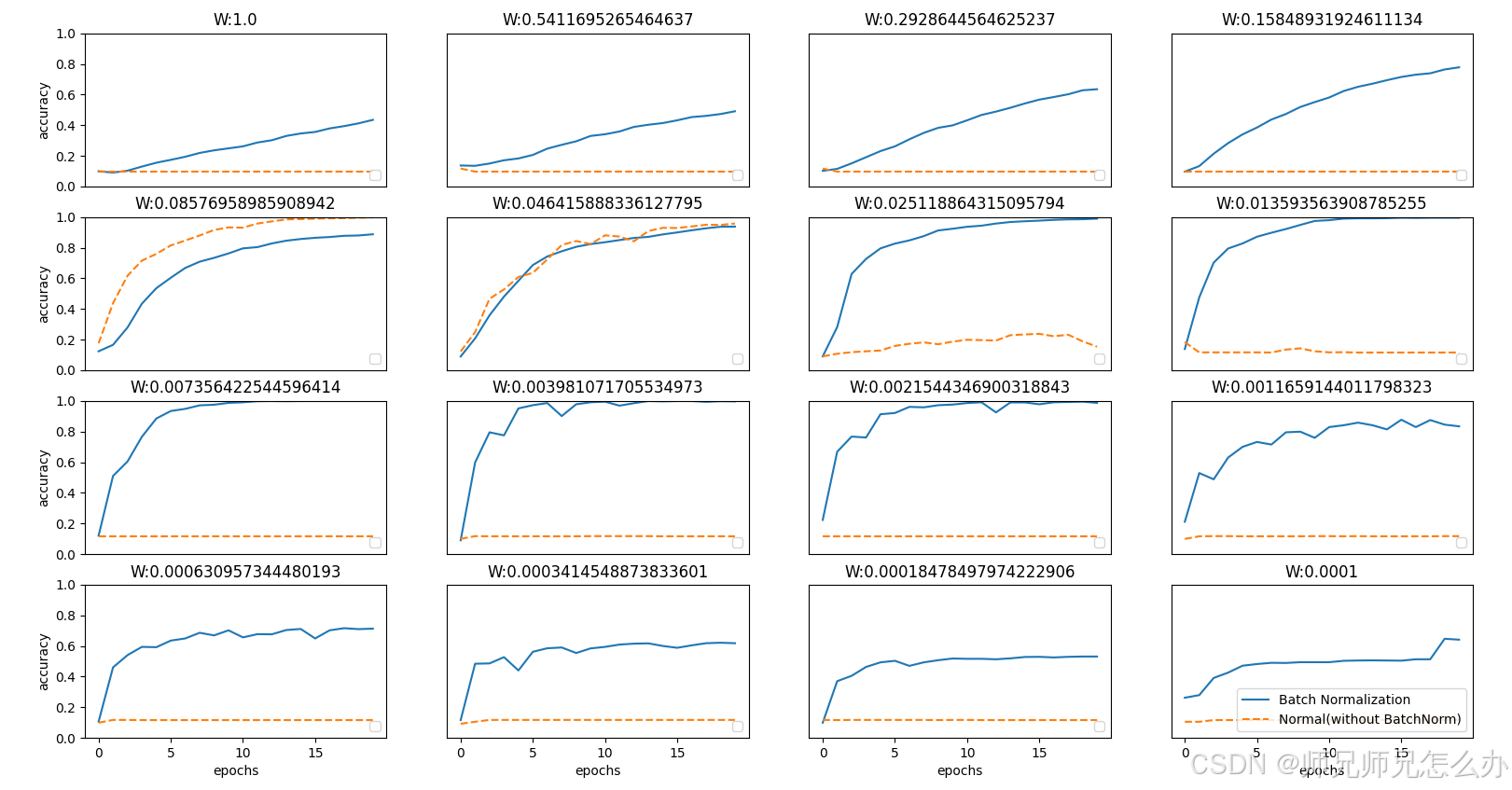
可以发现,几乎所有的情况下都是使用Batch Norm时学习进行得更快。同时也可以发现,实际上,在不使用Batch Norm的情况下,如果不赋予一个尺度好的初始值,学习将完全无法进行。
源码如下:
python
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 减少学习数据
x_train = x_train[:1000]
t_train = t_train[:1000]
max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
def __train(weight_init_std):
bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std, use_batchnorm=True)
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std)
optimizer = SGD(lr=learning_rate)
train_acc_list = []
bn_train_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for _network in (bn_network, network):
grads = _network.gradient(x_batch, t_batch)
optimizer.update(_network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
bn_train_acc = bn_network.accuracy(x_train, t_train)
train_acc_list.append(train_acc)
bn_train_acc_list.append(bn_train_acc)
print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
return train_acc_list, bn_train_acc_list
# 3.绘制图形==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)
for i, w in enumerate(weight_scale_list):
print("============== " + str(i + 1) + "/16" + " ==============")
train_acc_list, bn_train_acc_list = __train(w)
plt.subplot(4, 4, i + 1)
plt.title("W:" + str(w))
if i == 15:
plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
plt.plot(x, train_acc_list, linestyle="--", label='Normal(without BatchNorm)', markevery=2)
else:
plt.plot(x, bn_train_acc_list, markevery=2)
plt.plot(x, train_acc_list, linestyle="--", markevery=2)
plt.ylim(0, 1.0)
if i % 4:
plt.yticks([])
else:
plt.ylabel("accuracy")
if i < 12:
plt.xticks([])
else:
plt.xlabel("epochs")
plt.legend(loc='lower right')
plt.show()