一、决策树的基本定义
决策树通过对训练样本的学习,并建立分类规则,然后依据分类规则,对新样本数据进行分
类预测,属于有监督学习。
核心:所有数据从根节点一步一步落到叶子节点。
根节点:第一个节点。
非叶子节点:中间节点。
叶子节点:最终结果节点。
二、决策树的分类标准
1.ID3算法。
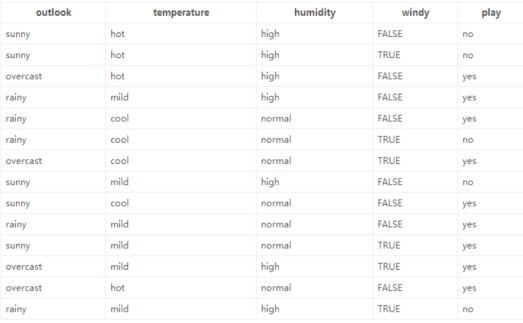
衡量标准:熵值:表示随机变量不确定性的度量,或者说是物体内部的混乱程度。
熵:熵值越小,该节点越"纯"。
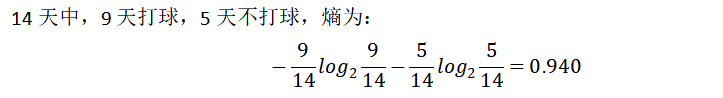
1)天气的划分
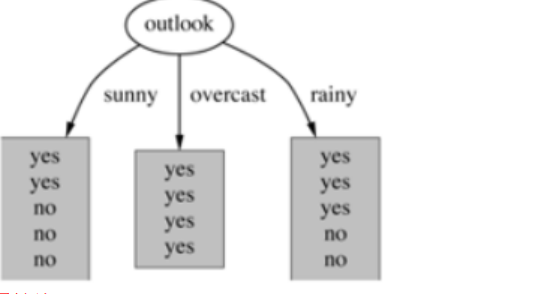
属性熵:
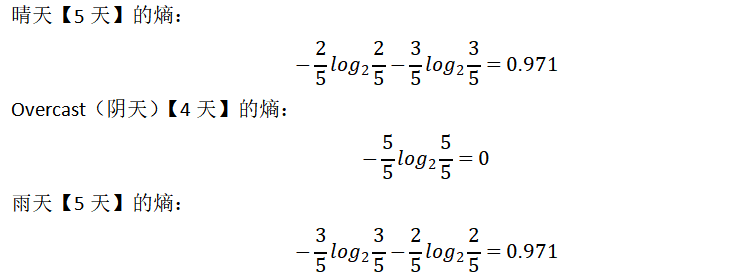
熵值计算:5/14*0.971+4/14*0+5/14*0.971=0.693
则信息增益为:0.940-0.693=0.247
天气的信息增益为0.247,依次算出其他的信息增益从大到小依次作为根节点
在决策树算法中,信息增益是特征选择的一个重要指标。它描述的是一个特征能够为整个系统带来多少信息量(熵),用于度量信息不确定性减少的程度。如果一个特征能够为系统带来最大的信息量,则该特征最重要,将会被选作划分数据集的特征。
2.C4.5算法。
衡量标准:信息增益率。
信息增益率:特征A对训练数据集D的信息增益比g(D,4)定义为其信息增益g(D,A)与训练数据集D的经验熵H(D)之比
C4.5算法是一种决策树生成算法,它使用信息增益比(gainratio)来选择最优分裂属性,具
体步骤如下:
1、计算所有样本的类别熵(H)。
2、对于每一个属性,计算该属性的熵【也为自身熵】(Hi)。
3、对于每一个属性,计算该属性对于分类所能够带来的信息增益(Gi=H-Hi)。
4、计算每个属性的信息增益比(gain ratio=Gi/Hi)
天气的信息增益为:0.247
天气的自身熵值:5天晴天、4天多云、5天有雨。
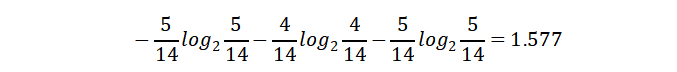
信息增益率:0.247/1.577 = 0.1566
3.CART决策树。
衡量标准:基尼系数
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性,基尼指数值越大,样本集合的不确定性也就越大,这一点与熵相似。
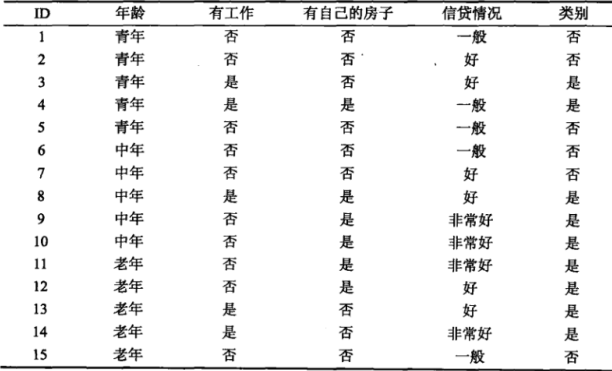
青年(5人,2人贷款)的基尼系数:
非青年(10人,7人贷款)的基尼系数:

三、决策树剪枝
剪枝为了防止过拟合
预剪枝策略:1.限制树的深度
2.限制叶子节点的个数以及叶子节点的样本数
3.基尼系数
四、决策树回归树模型
解决回归问题的决策树模型即为回归树。
特点:必须为二叉树

1.计算最优切分点
因为只有一个变量,所以切分变量必然是x,可以考虑如下9个切分点:
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5
1)1.5切分点的计算
将数据分为第一部分(1,5.56)和后面第二部分
2)计算损失
C1=5.56
C2=1/9(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5
Loss = (5.56-5.56)^2 + (5.7-7.5)^2+(5.91-7.5)^2+...+(9.05-7.5)^2 =15.72
3)再从分开的两部分数据找到最优切分点
五、决策树API
class sklearn.tree.DecisionTreeClassifier (criterion='gini' , splitter='best' , max_depth=None , min_samples_split=2 , min_samples_leaf=1 , min_weight_fraction_leaf=0.0 , max_features=None , random_state=None , max_leaf_nodes=None , min_impurity_decrease=0.0 , min_impurity_split=None , class_weight=None , presort=False)
1.criterion :gini or entropy 【采用基尼系数还是熵值衡量,默认基尼系数】
2.splitter: best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候)【默认best,无需更改】
3.max_features:(表示寻找最优分裂时需要考虑的特征数量,默认为None,表示考虑所有特征。),log2,sqrt,N 特征小于50的时候一般使用所有的 【默认取所有特征,无需更改】
4.max_depth: 表示树的最大深度
5.max_leaf_nodes :(最大叶子节点数)
6.min_samples_split :(表示分裂一个内部节点需要的最小样本数,默认为2)
六、AUC性能测量
在机器学习中,性能测量是一项基本任务。因此,当涉及到分类问题时,我们可以依靠AUC - ROC曲线。当我们需要检查或可视化多类分类问题的性能时,我们使用AUC(曲线下面积)ROC(接收器工作特性)曲线。它是检查任何分类模型性能的最重要评估指标之一。
TPR为召回率,FPR为FP/TN+FP
python
y_proba=tr.predict_proba(x_test)
a=y_proba[:,1]
from sklearn.metrics import roc_curve, auc # 得到不同阈值的roc
# 计算ROC曲线的点
fpr,tpr,thresholds=roc_curve(y_test,a)#用来计算不同阈值下的fpr和tpr,
auc_result=auc(fpr,tpr)
# 绘制ROC曲线
plt.figure()
plt.plot(fpr,tpr,color='darkorange',lw=2,label='ROC curve(area=%0.2f)'%auc_result)
plt.plot([0,1],[0,1],color='navy',lw=2,linestyle='--')#函数来绘制一条从点(o,o)到点
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
plt.xlabel('FalsePositive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend()
plt.show()通过roc_curve函数来计算不同阈值下的fpr和tpr,再通过auc函数填入fpr,tpr来计算AUC
七、随机森林
1.集成学习
1.集成学习的含义:
集成学习是将多个基学习器进行组合,来实现比单一学习器显著优越的学习性能。
2.集成学习的代表:
bagging方法:典型的是随机森林
boosting方法:典型的是Xgboost
stacking方法:堆叠模型
3.集成学习的应用:
1)分类问题集成。
2)回归问题集成。
3)特征选取集成。
2.随机森林
特点:(1)数据采样随机(2)特征选取随机(3)森林(4)基分类器为决策树
优点:
1.具有极高的准确率。
2.随机性的引入,使得随机森林的抗噪声能力很强。
3.随机性的引入,使得随机森林不容易过拟合。
4.能够处理很高维度的数据,不用做特征选择。
5.容易实现并行化计算。
缺点:
当随机森林中的决策树个数很多时,训练时需要的空间和时间会较大。
1
2
3
4
5