PaCon：一种用于识别编程提交中问题求解策略的符号分析方法

基本信息

PaCon: A Symbolic Analysis Approach for Tactic-Oriented Clustering of Programming Submissions
SPLASH-E 2021: Proceedings of the 2021 ACM SIGPLAN International Symposium on SPLASH-E (October 2021)

博客贡献人

糖瓶

作者
Yingjie Fu, Jonathan Osei-Owusu, Angello Astorga, Zirui Neil Zhao, Wei Zhang, Tao Xie

摘要

编程课程的注册人数正急剧增加。为了保持编程课程的教学质量，教师需要能够大规模地理解学生表现并据此提供反馈的方法。例如，对于教师而言，识别编程提交中使用的不同解题方法（本文定义为策略，tactics ）非常重要。然而，由于策略存在多个抽象层级，且同一策略的实现具有高度多样性，教师手动完成策略识别任务不仅具有挑战性，而且耗时费力。针对这一任务，我们提出了 PaCon，一种对功能正确的编程提交进行聚类的符号分析方法，旨在提供一种识别策略的途径。具体而言，PaCon 根据程序的语义特征------**路径条件（path conditions）**对提交进行聚类。由于专注于程序语义，PaCon 能够避免因提交之间细微的语法差异而产生过多聚类的问题。我们在真实数据集上的实验结果表明，PaCon 能够生成数量合理的聚类，每个聚类都能有效地将那些语法多样性高但共享等效路径条件语义的提交归为一组，从而为策略识别提供了一种有前景的方法。

1.引言

近年来，编程课程，尤其是在线编程课程，吸引了来自世界各地的大量学生注册。随着班级规模的扩大，检查编程提交以进行评分、构建参考答案以及准备针对性的教学材料变得越来越耗时。虽然已有部分自动化工具被提出以协助在线编程课程的教师，但这些工具通常侧重于提交的功能正确性，或如何将错误的提交修改为功能正确的提交。

然而，识别学生解决问题的方法（本文称之为策略）也同样重要，主要原因有三点。首先，识别策略可以帮助教师在作业描述中包含与策略相关的约束时，实现更高效的评分。例如，给定作业"在不排序的情况下找出数组中任意两个元素的最大差值"，一个首先对输入数组元素进行排序，然后用最大元素减去最小元素的提交不应获得满分，因为它违反了"不排序"的要求。由于提交中与策略相关的特征无法通过程序输出来反映，如果没有工具辅助，教师必须手动检查每个提交，以确认这些策略相关的约束是否得到满足。其次，识别策略可以帮助教师高效地提出多样化的参考答案，这对于半自动化工具生成定制反馈非常有价值。一些现有的反馈生成工具要求用户提供模板或模型解决方案以与编程提交进行匹配，但对于经验不足的教师来说，提前列出全面的模板具有挑战性。通过识别学生功能正确提交中使用的不同策略，教师可以更轻松地制作参考答案。第三，识别策略可以帮助教师准备针对性和适应性的教学材料。例如，当要求学生"找出给定数组中第 k 大的数"时，解决该作业的一个好方法是使用"分治法"，但许多学生可能会使用"排序"的方法来解决这个问题。通过识别所使用的策略，教师可以了解学生提交中策略的分布情况，然后向全班讲解"排序"与"分治"方法之间的关系。

识别编程提交中的策略是一项具有挑战性且耗时的任务，主要原因有二。首先，很难给出一个清晰的策略定义，因为策略的识别反映了不同的抽象层级，这取决于具体的作业和教学要求。例如，当我们关注排序作业时，提交的不同策略可以分为冒泡排序、插入排序和归并排序等已知策略。但是对于"找出数组中第 k 大元素"的作业，策略可以分为分治法、排序和暴力法。在后一种作业中，一个恰当清晰的策略定义不应该捕捉具体的排序算法。其次，采用相同策略的程序在代码的语法组织方式上可能截然不同。例如，给定计算的问题，循环和递归都可以实现相同的策略------即"通过计算阶乘来计算 "，但它们表现出明显的语法差异。

为了帮助识别编程提交中的策略，本文提出了 PaCon，一种对功能正确的编程提交进行聚类的符号分析方法，旨在提供一种识别策略的途径。PaCon 利用来自符号执行的路径条件来对提交进行聚类。

关键定义： 使用给定的输入值执行程序会运行（即遵循）程序中的一条路径。该路径的路径条件（path condition），也称为给定输入值的路径条件，代表了输入约束：(1) 所有运行该路径的输入值必须满足该约束；(2) 满足该约束的输入值必然导致程序运行该路径。

PaCon 的核心洞察在于，提交所采用的输入空间划分（input-space-partitioning）策略可以提供一种寻找策略的途径，而这种策略可以基于输入值的路径条件推导出来。具体而言，路径条件反映了提交的程序如何将输入空间划分为多个等价类，每个等价类包含遵循同一路径的所有输入值。重温前面描述的例子：两个通过计算阶乘来计算的提交，一个使用循环，另一个使用递归。尽管这两个提交的实现不同，但它们的程序共享基于路径条件推导出的相同的输入空间划分策略。

基于这一洞察，PaCon 的工作流程包含三个主要步骤：(1) 测试生成，(2) 路径条件收集，以及 (3) 基于路径条件的聚类。PaCon 首先运行结构化测试生成器来生成测试输入（简称测试），归一化生成的测试集，然后收集这些测试的路径条件。在聚类的最后一步，PaCon 确保同一聚类中的提交对于每个生成的测试必须具有语义等效的路径条件。

我们在真实数据集上进行的评估表明，PaCon 生成的聚类数量是合理的，且 PaCon 能够生成这样的聚类：每个聚类有效地将那些语法多样性高但共享等效路径条件语义的提交归为一组。通过手动检查 PaCon 生成的聚类，我们发现这些聚类可以很好地指示提交在解决目标问题的方式上的差异。这些结果表明，PaCon 可以提供一种识别策略的有前景的方法。

本文的主要贡献如下：

我们唤起了对识别学生编程提交中策略的关注。
我们提出了一种名为 PaCon 的符号分析方法，用于对功能正确的编程提交进行聚类，以提供一种识别策略的途径。
我们在真实数据集上进行了评估，以评估 PaCon 在聚类功能正确编程提交方面的表现。

2. 动机示例

本节展示一个动机示例，以说明 (1) 聚类方法在帮助识别策略方面面临的挑战，以及 (2) 现有方法为何在此任务中失败。

Listings 1-3 展示的示例关于"在一个整数数组中找出任意两个元素的最大差值"的编程作业，其中输入 a 不为空。在Listings 1-3 中，max-difference(A)、max-difference(B) 和 max-difference(C) 展示了三个提交的快照，它们在功能上都是正确的。

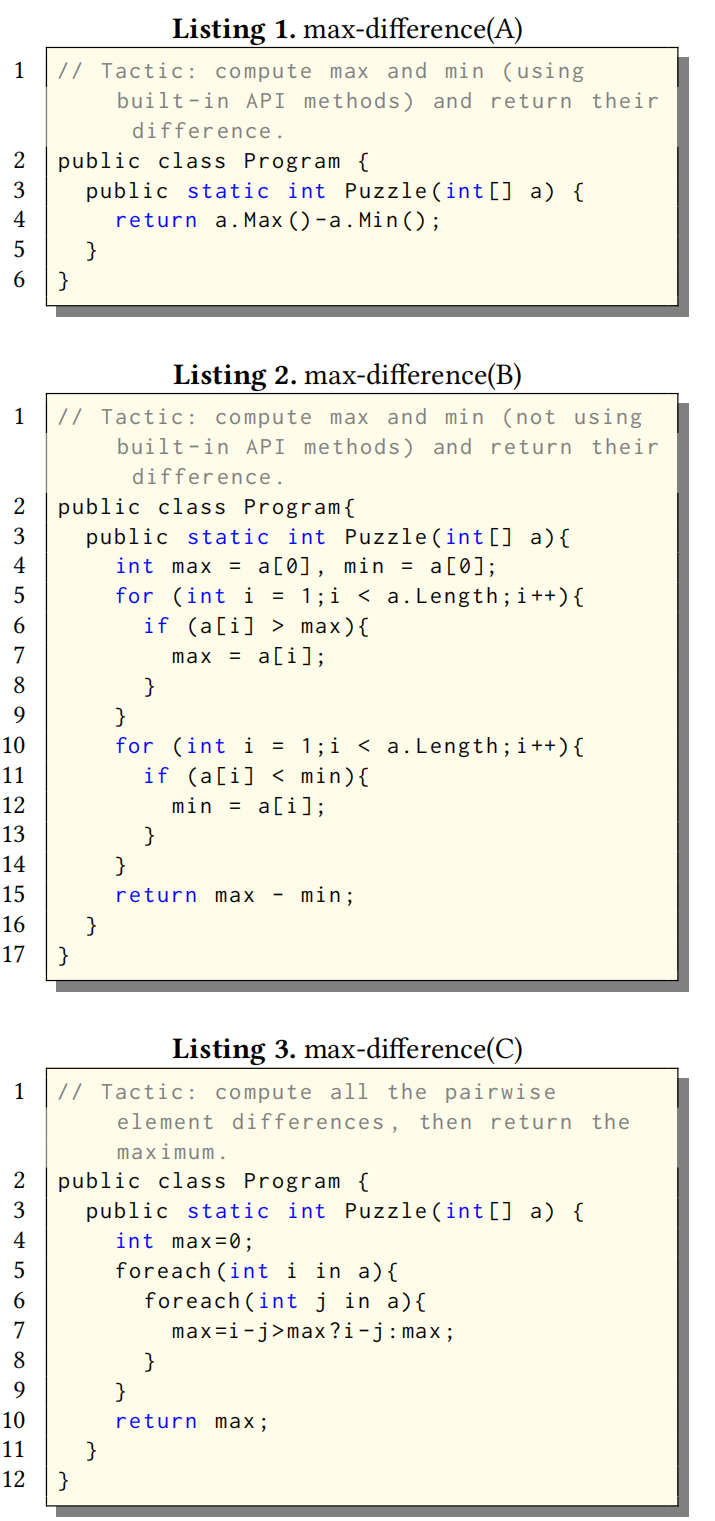
在这三个提交中，max-difference(A) 和 max-difference(B) 在解题方式上具有相似性。具体而言，前两个提交都先找出数组的最大元素和最小元素，然后用最大元素减去最小元素以获得预期的返回值。提交 max-difference(C) 则通过检查所有元素对并比较差值来解决问题。

然而，这三个提交在变量命名和代码结构上也存在差异。在变量名方面，max-difference(A) 和 max-difference(B) 都使用变量 max 记录最大值，使用变量 min 记录最小值，但 max-difference(C) 直接使用 max 记录预期的最大差值。在代码结构方面，max-difference(A) 使用了内置的 Max 和 Min API 方法，而 max-difference(B) 使用两个 for 循环分别识别数组中的最大和最小整数元素。为了比较元素间的所有成对差值，max-difference(C) 实现了一个两层嵌套的 for 循环。

在这个例子中，如果不考虑 Max 和 Min API 方法的具体实现，一个能够帮助识别策略的理想聚类方法应当能够识别出 max-difference(A) 和 max-difference(B) 在解题方式上的相似性，并将它们归为一组。至于 max-difference(C) 的提交，由于它使用了不同的策略，理想的聚类方法不应将其与 max-difference(A) 和 max-difference(B) 放入同一个聚类中。

许多现有的基于语法的方法依赖于特定的程序特征，如控制流、变量序列和抽象语法树（AST）来聚类提交。这些方法只有在特定的程序特征相同或高度相似时，才会将两个提交放入同一个聚类。例如，CLARA 只有在两个提交的循环结构匹配时才将它们归为一类。OverCode 要求同一聚类中两个提交的语句集合（重命名变量后）必须相同。这两种方法都会将前两个提交放入不同的聚类中。

从上述例子可以看出，现有的基于语法的方法没有考虑程序的解题方式，因此它们在帮助识别策略方面效果不佳。为了识别策略，我们建议将语义程序信息纳入考量。

3. 方法

本节介绍我们用于聚类编程提交的符号分析方法 PaCon，它根据程序的语义特征------路径条件对编程提交进行聚类。

3.1 PaCon 概览

给定一个编程问题，PaCon 接收一组功能正确的提交作为输入，并输出一组提交聚类。为了简化随后的讨论，我们假设每个提交都有一个名为 Puzzle 的静态方法，该方法通过参数 args 接收输入，并通过返回值返回结果。参数和返回值的类型可以是基本类型或类。

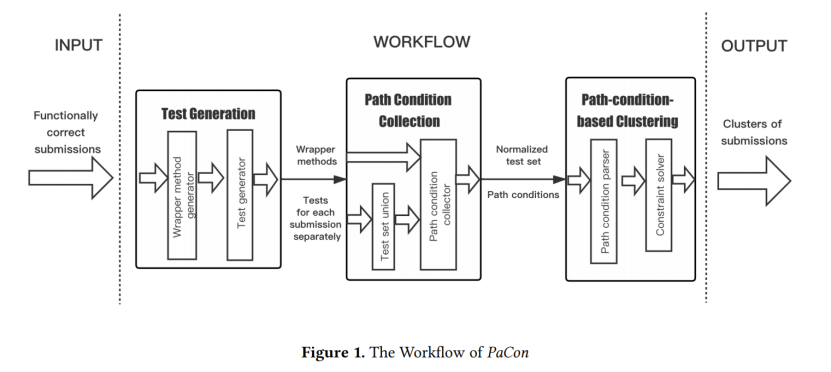
图1 展示了 PaCon 的工作流程概览，它包含三个步骤：(1) 测试生成，(2) 路径条件收集，以及 (3) 基于路径条件的聚类。第一步的目的是生成高代码覆盖率的测试，这有助于反映提交的程序行为。在第二步中，对于每一个提交，PaCon 收集其运行每个测试时的路径条件。最后，PaCon 根据路径条件语义的等价性对提交进行分组，并输出一组提交聚类。

3. 2 测试生成

这一步的目的是获得具有高代码覆盖率（如高语句、块、分支、数据流和路径覆盖率）的测试。理想情况下，测试应全面采样输入值，这有助于运行不同的路径从而产生不同的路径条件，以区分不同提交之间的输入空间划分策略。

这一步包含两个模块：包装方法（wrapper method）生成器和测试生成器。PaCon 首先为编程问题构建一个包装方法。该包装方法可以被视为 Puzzle 方法的一个参数化单元测试。该包装方法可以根据任何功能正确解决方案的参数类型和返回类型自动生成。

Listing 4 展示了第2节中 max-difference 问题的简化版包装方法。如果存在任何前置条件（即输入参数的约束），教师可以在生成的包装方法中手动添加前置条件。注意，每个问题只需要一个包装器，因此即使手动准备包装方法，对教师来说也是可接受的工作量。

包装方法准备好后，PaCon 与结构化测试生成器交互，以获取高代码覆盖率的测试。注意，实现程序中路径的完全覆盖可能是不可能的，例如，如果循环迭代次数是一个没有边界约束的整数输入参数值，那么将存在无限数量的路径和路径条件。结构化测试生成器的目标通常可以配置为实现高语句、块、分支或数据流覆盖。在 PaCon 的实现中，采用的结构化测试生成器是 Pex ，其默认配置是生成高块覆盖率（block coverage）的测试。对于第2节所示的激励性示例，Pex 为 max-difference(A)、max-difference(B) 和 max-difference(C) 生成的测试数量分别为1 、6 和2 。

3.3 路径条件收集

在这一步中，PaCon 旨在收集每个测试衍生出的路径条件。使用测试中的给定输入值执行程序会运行（即遵循）程序中的一条路径。该路径的路径条件，也称为给定输入值的路径条件，代表了输入约束：(1) 所有运行该路径的输入值必须满足该约束；(2) 满足该约束的输入值必然导致程序运行该路径。

与被执行路径上的分支条件不同，路径条件仅包含涉及输入参数变量的约束，而不涉及程序中的任何局部变量。例如，对于Listing 2中的提交，第6行和第11行分别有两个分支条件，它们都涉及局部变量（分别为 max 和 min）。给定输入数组，路径条件是 a[1]>a[0] && a[1]>=a[0]，而不是 a[1]>max && a[1]>=min 。

注意，为了对提交进行聚类，PaCon 需要它们在同一测试下的路径条件。但是结构化测试生成器通常不能保证每次运行都产生相同的测试集，并且为任意两个提交生成的测试集也可能不同。例如，对于Listing 1 中的 max-difference(A)，Pex 生成的一个测试是 [18,18]，而对于Listing 3 中的 max-difference(C)，Pex 生成了两个测试：[32,48] 和 [40,41,18] 。因此，有必要对所有提交使用同一组测试集，以便我们可以在输入空间上公平地比较每个提交产生的路径条件。

在这一步中，PaCon 通过对第一步为所有提交生成的所有测试取并集来进行测试归一化，并将它们放入一个仅保留唯一测试的集合中。然后，PaCon 调用路径条件收集器对每个提交收集归一化测试集中测试的路径条件。通过这种方式，max-difference(A)、max-difference(B) 和 max-difference(C) 的归一化测试集包括[18, 18], [32, 48], [40, 41, 18] 等。

我们利用 Pex 作为路径条件收集器。具体而言，Pex 提供了一种获取测试中输入值的路径条件的便捷方式，即调用 Pex 提供的 GetPathConditionString API 方法。我们直接返回调用 GetPathConditionString 的结果作为收集到的路径条件。

3.4 基于路径条件的聚类

在这一步中，PaCon 进行基于路径条件的聚类，根据等效的路径条件语义将功能正确的提交分组为一组提交聚类。

基于路径条件聚类的高层思想是，对于同一问题的两个给定正确提交
和，PaCon 检查和在归一化测试集中的每个测试上是否具有语义等效的路径条件。如果是，PaCon 将它们放入同一个聚类中。值得一提的是，提交之间的等价性是可传递的。因此，当评估一个提交是否属于某个给定聚类时，PaCon 只需将其与该聚类中随机选择的一个提交进行比较，而不是与其中的所有提交进行比较。

算法1 展示了基于路径条件聚类的伪代码。PaCon 遍历所有正确的提交（第 2 行）。对于每个提交，PaCon 遍历现有的聚类，通过比较路径条件来检查是否属于其中任何一个。具体来说，PaCon 随机选择属于现有聚类c的一个提交 r。作为代表（第 5 行），然后调用函数 isEq 来确定s和r是否等效（第 6 行）。如果 isEq 返回 True（第7 - 9行），则聚类c可被视为提交s所属的聚类，PaCon 将s加入聚类c并继续处理下一个提交。如果当前聚类集合为空或未找到提交s的聚类，PaCon 将建立一个新聚类并将s放入其中（第 10-12行）。当所有提交都被放入各自的聚类后，PaCon 返回集合c作为提交的聚类结果。

如算法2所示，两个提交s1和s2的等价性由其路径条件的语义等价性决定。具体而言，对于每个测试 t∈T，s1和s2的路径条件分别表示为pc1和pc2。当且仅当pc1和pc2的语义对于T中的每个测试都等效时，s1和s2被认为是等效的。这种等价性专门用于识别程序如何将输入空间划分为等价类。理想情况下，对于同一聚类中的两个提交s1 和s2以及任意输入t，s1 和s2对t的等价类应该是相同的。我们通过路径条件解析器和约束求解器 Z 来实现路径条件的语义比较。

4. 评估

本节旨在通过实证调查 PaCon 生成的聚类数量、每个生成聚类中的语法多样性（与基于语法的工具生成的结果相比），并探索 PaCon 生成的聚类能反映什么样的策略，来回答三个研究问题。

为了帮助回答前两个研究问题，除 PaCon 外，我们还研究了两种基于语法的聚类工具，它们基于两个可处理 C# 程序的（近）重复代码检测工具：JetBrains 的 dupFinder (DF) 和 Microsoft 的 Near-Duplicate (ND) 。具体而言，为了从（近）重复代码检测结果中生成聚类，如果两个提交之间存在任何重复代码片段，我们将它们放入同一个聚类。对于与任何其他提交都没有共享重复代码片段的每个提交，我们将该提交放入一个单独的聚类中。

4.1 研究问题

RQ1：与基于语法的工具相比，PaCon 生成的聚类数量是多少？

RQ1 的目的是调查 PaCon 在多大程度上可以潜在地减少教师检查编程提交的工作量。PaCon 的一个目标是减轻教师检查大量提交的负担。理想情况下，在聚类的帮助下，教师只需从每个聚类中选择一个代表进行检查，而不是查看所有提交。然而，如果聚类方法生成的聚类数量仍然很大，教师检查所有代表仍然是沉重的负担，那么该聚类方法在实践中就是不可行的。为了回答这个问题，我们将 PaCon 生成的聚类数量与 ND 和 DF 生成的聚类数量进行了比较。

RQ2：PaCon 生成的聚类中包含的提交，其语法多样性如何？

RQ2 的目的是评估 PaCon 将具有语法差异但路径条件语义等效的提交聚类在一起的能力。为了回答这个问题，我们评估了每个 PaCon 生成的聚类（简称 PaCon 聚类）内部的语法多样性。具体而言，我们将 PaCon 聚类内的语法多样性度量为该 PaCon 聚类中的提交所属的基于语法的聚类（即由基于语法的工具如 ND 或 DF 生成的聚类）的数量。该计数越高，PaCon 聚类的语法多样性就越高。

RQ3：PaCon 生成的聚类能反映出什么样的策略？

如第1节所述，识别策略的挑战之一来自于随需求变化的策略定义，因此很难将每个提交中使用的策略标记为基准真值（ground truth）。RQ3 的目的是调查 PaCon 可以帮助教师识别什么样的策略。为了回答这个问题，我们手动检查每个 PaCon 聚类，并总结评估对象中每个作业提交所使用的策略。

4.2 评估对象

评估对象包括两个真实数据集来源。

Code-Hunt。Code-Hunt 数据集包含来自48小时全球编程竞赛的提交。竞赛有四个部分，每个部分包含六个谜题，参与者（学生）在时间限制内可以无限次尝试解决编程问题。我们选择这个数据集是因为其谜题的难度代表了入门级编程课程的作业，同时也因为该数据集被用于相关工作。

在 Code-Hunt 数据集的24个谜题中，我们首先选择提交中至少包含一个分支的12个谜题。考虑到 PaCon 仅专注于聚类功能正确的提交，我们进一步排除了功能上与 Code-Hunt 给定解决方案不一致的提交，仅保留功能正确的提交。此外，参加竞赛的学生可以使用 Java 或 C# 。由于我们的 PaCon 实现包括 Pex（支持 C# 但不支持 Java）作为测试生成器，我们使用转换器将 Java 提交转换为 C# 程序，并仅包括那些可以成功编译的结果 C# 程序。最后，我们排除剩余正确提交少于10个的谜题。表1 展示了我们评估中包含的谜题描述。表2 的第二列显示了每个谜题在评估中包含的提交数量。

Sorting (排序)。除了 Code-Hunt 数据集，我们的评估对象还包括排序数据集，由许多实现排序功能的程序组成。我们选择排序问题是因为 (1) 排序是计算机科学编程课程中教授的经典问题，(2) 我们想知道 PaCon 能识别的策略与那些标记良好的解题方式有何关联。我们收集了带有五个不同标签的排序程序：冒泡排序、堆排序、插入排序、快速排序和归并排序。我们通过 Google 以每个标签作为关键词在 C# 程序中搜索，获得了这五种排序的程序。冒泡排序、堆排序、插入排序、快速排序和归并排序的标签分别包含 17、11、16、10 和12个程序，总共66个程序。

4.3 RQ 结果：生成的聚类数量

表2 显示了聚类结果的统计数据。前两列指示作业名称和该作业功能正确提交的总数。PaCon、ND 和 DF 生成的聚类数量分别显示在最后三列、和中。

根据统计数据，对于每个 Code-Hunt 谜题，PaCon 最多生成10 个聚类，对于排序问题生成 15个聚类。对于所有作业，PaCon 生成的聚类数量都小于 ND 和 DF 。随着提交数量的增加，这种差距更加明显。Sector3-Level2 的 99个提交仅被 PaCon 分为 5个聚类，而 ND 和 DF 生成的聚类数量分别为40 和68 。相比之下，Sector4-Level2 的 17个提交被 PaCon 分为 7个聚类，ND 为 10个，DF 为 14个。

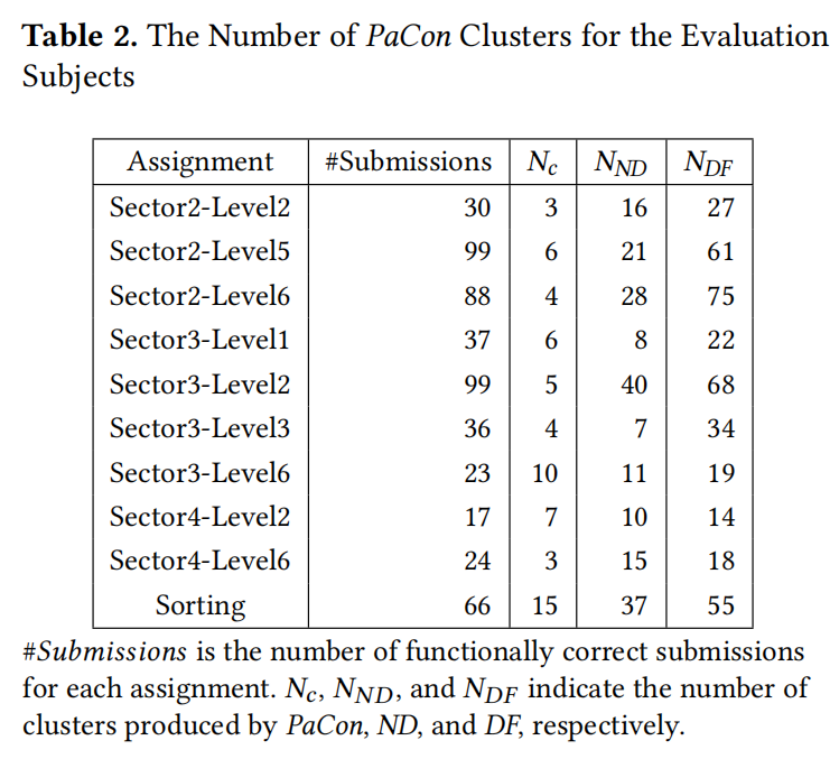
这一趋势符合我们的直觉：对于特定的编程问题，采用相同策略的提交可能具有截然不同的代码语法组织方式，随着提交数量的增加，这种差距往往也会增加。总之，PaCon 可以生成数量合理的聚类，且 PaCon 生成的聚类数量远小于两个基于语法的工具（ND 和 DF）。

4.4 RQ 结果：聚类的语法多样性

图2 显示了每个作业的 PaCon 聚类语法多样性的分布。对于所有作业，PaCon 都能生成语法多样性至少为 2 的聚类。此外，对于大多数作业，语法多样性不小于 2的聚类占总聚类的至少40 % 。而且，对于 Sector3-Level2、Sector2-Level2、Sector2--Level15、Sector2-Level16 等，PaCon 甚至产生了语法多样性大于10 的聚类。

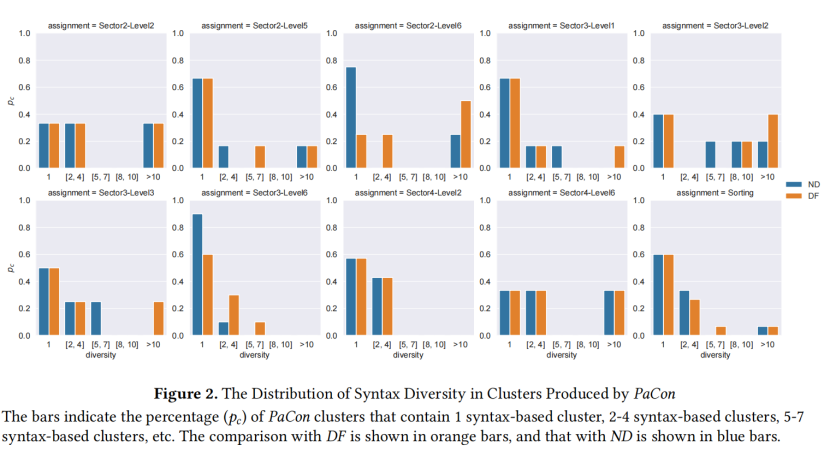
当使用 DF 进行基于语法的聚类时，除两个作业（Sector2-Level5 和 Sector3-Level1）外，所有作业中语法多样性至少为 2的聚类百分比都不低于 40% 。在 Sector2-Level5 中，该比例甚至高达 75% 。相比之下，当使用 ND 进行基于语法的聚类时，对于 Sector2-Level5、Sector2-Level6、Sector3-Level1 和 Sector3-Level6，语法多样性仅为 1的聚类比例超过 60% 。特别是对于 Sector3-Level6，只有 10% 的 PaCon 聚类语法多样性大于 1。

总之，PaCon 可以有效地将具有语法差异但路径条件语义等效的提交聚类在一起。

4.5 RQ 结果：聚类反映的策略

我们手动检查了 PaCon 生成的聚类，并根据每个评估对象的聚类总结了策略。由于篇幅限制，在本小节中，我们仅讨论两个评估对象的分析结果。完整的分析结果可在 https://sites.google.com/view/paconproj/ 找到。

4.5.1 Sector2-Level5 的案例

表3 显示了 Sector2-Level5 的详细结果。我们根据 PaCon 的聚类结果总结了三种策略："找出数组的最大和最小元素，然后返回它们的差值"，"先排序，然后返回 |a[length-1]-a[0]|"，以及"计算所有成对元素的差值，然后返回最大值" 。

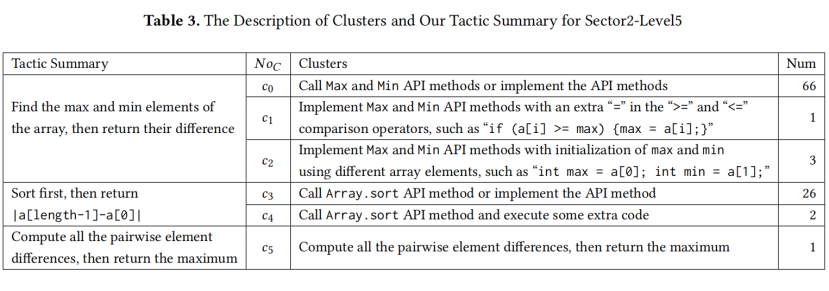
对于表中的第一种策略，PaCon 生成了三个聚类，其中大多数提交落入聚类。聚类中的提交要么调用内置的 Max 和 Min API 方法，要么自己实现这两个 API 方法。还有少数其他提交采用与类似的策略，但未被归入聚类。例如，聚类包含一个提交，该提交在实现 Max 和 Min API 方法时，在 >= 和 <= 比较操作符中多了一个 =。为了获得数组 a 中的最大元素，大多数提交使用诸如 if (a[i]>max) {max=a[i];} 的语句，而聚类中的提交使用语句 if(a[i]>=max) {max=a[i];} 。此外，聚类包含三个提交，它们使用与或不同的数组元素初始化 max 和 min 变量。

虽然带有额外 = 的操作符差异看似只是语法性质的，但在某些情况下，它确实导致了路径条件的语义差异。由于额外的 =，不仅操作符改变了，而且比较也发生在不同的元素对之间。例如，考虑我们在计算数组 a=[2,2 ,1 ,3 ] 中的最大元素。当我们使用 if(a[i]>max) 更新 max 时，路径条件是 a[1]<=a[0] && a[2]<=a[0] && a[3]>a[0] 。但是当我们使用 if(a[i]>=max) 更新时，路径条件变为 a[1]>=a[0] && a[2]<a[1] && a[3]>=a[1] 。

对于表中的第二种策略，PaCon 生成了两个聚类和，大多数提交落入聚类。聚类中的提交首先对给定的数组元素进行排序，而除了进行排序外，中的提交还执行了一些额外的代码，没有这些代码提交仍有相同的返回值，但其执行在路径条件中引入了额外的约束。

对于表中的第三种策略，有一个聚类仅包含一个提交，该提交计算所有成对元素的差值，然后返回最大值。

4.5.2 排序问题的案例

图3 展示了 PaCon 在排序程序上的聚类结果散点图。x 轴指示 PaCon 生成的聚类，y 轴指示排序程序的五种不同标签。程序的数量由散点的大小反映。

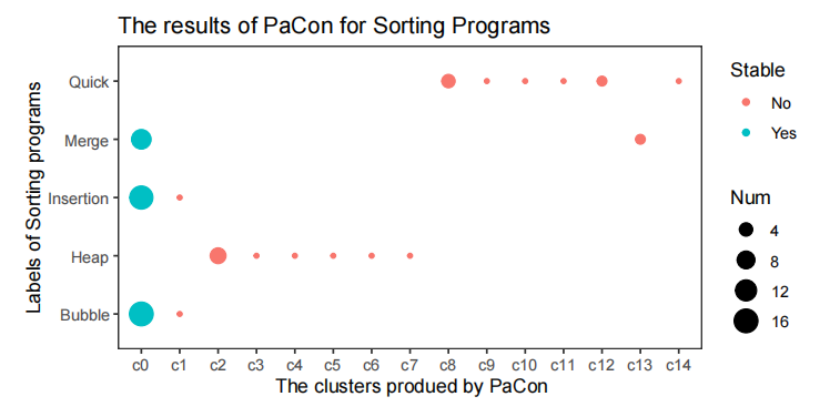
根据图3 显示的结果，PaCon 产生的聚类结果并非识别不同的排序标签，而是反映了排序的稳定性（stability）。关键定义：如果数组中任意两个值相等的元素在程序输出中的顺序总是与它们在输入中出现的顺序一致，则该排序程序是稳定的。具体而言，中的程序都是稳定的排序程序，包括大多数冒泡排序程序、大多数插入排序程序和大多数归并排序程序。其他 14 个聚类中的程序都是不稳定的排序程序。

聚类包含一个冒泡排序程序和一个插入排序程序。对于中实现冒泡排序的程序，它不是比较相邻元素，而是在每一轮中将固定元素与其后的每个元素进行比较，并在发现逆序时交换这两个元素。它不是一个稳定的排序程序。聚类中的插入排序程序实际上实现了选择排序，也是不稳定的。

聚类包含两个实现归并排序的程序。当合并两个有序子数组时，程序仅在 a[i] < a[j] 时将 a[i] 放在 a[j] 的左边（a[i] 是左子数组中的元素，a[j] 是右子数组中的元素）。如果它们的值相等，此操作会导致这两个元素 a[i] 和 a[j] 的相对顺序反转，因此这两个程序不是稳定的排序程序。

其余 12 个聚类中的每一个程序都只带有一个标签。这些程序实现的是堆排序或快速排序，它们都是不稳定的。

剩下的问题是，为什么 PaCon 将那些不稳定的排序程序分到了不同的聚类中。关键原因在于，用于暴露某个不稳定排序程序不稳定性的一组数组输入值，可能不同于用于暴露另一个不稳定排序程序不稳定性的一组输入值。例如，考虑两个快速排序程序
和，它们使用不同的标准来选择基准值（pivot），以及一个输入数组。假设程序取最左边的元素作为基准值，程序取最右边的元素作为基准值。和都将小于的元素放在其左边，将不小于的元素放在其右边。排序后，的输出仍然是，但的输出变为。虽然和都是不稳定的，但输入暴露了的不稳定性，却没有暴露的不稳定性。回顾一下，PaCon 要求同一聚类中的程序对于每个生成的测试必须具有等效的路径条件，因此 PaCon 将不稳定的排序程序分为了不同的聚类。

为了进一步确认我们的发现，我们在排序输入中添加了"所有元素均不同"的前置条件后，PaCon 将所有排序算法归为了同一个聚类。

4.6 结果总结

在我们的评估中，PaCon 生成的聚类数量是合理的，并且远少于基于语法的工具生成的数量。同时，这些聚类有效地将那些语法多样性高但共享等效路径条件语义的提交归为一组。基于我们的手动分析，PaCon 生成的聚类有望表征提交在解决目标问题方式上的差异。对于排序问题，虽然 PaCon 没有帮助识别常见的排序算法，但它仍然可以区分排序程序的一个重要特征：排序程序是否稳定。

5. 讨论

PaCon 在当前的实现和设计上存在两个主要局限性。首先，PaCon 的实现包含一个约束求解器（如 Z3 ）来检查路径条件的等价性，但存在一些 Z3 无法处理的情况（如关于 HashSet 的约束）。如果发生这种情况，PaCon 直接将两个路径条件视为不等效（如果它们的字符串形式不同），并可能将使用相同策略的提交分为单独的聚类。在我们的评估中，PaCon 在聚类 Sector3-Level5 的提交时遇到了这种情况。

其次，PaCon 使用路径条件的语义等价性来聚类提交。它更关注程序的语义，并且在面对许多语法差异时具有鲁棒性。然而，这种权衡既有好处也有局限性。当两个提交使用了两种不同的策略，且策略差异体现在某些程序特征（如路径条件内约束的句法组合）中，但未影响路径条件的语义时，PaCon 会将这两个提交放入同一个聚类。在我们的评估中，PaCon 在聚类 Sector4-Level2 的提交时遇到了这种情况。

6. 相关工作

由于计算机科学课程的不断发展，编程提交的聚类成为帮助快速检查大量提交的一种有吸引力的方法。针对这一任务，已有大量工作被提出。本节讨论了一些密切相关的方法。

CLARA 、MistakeBrowser 和 TipsC 均旨在为错误的提交提供反馈。CLARA 和 TipsC 都对正确的编程提交进行聚类。具体而言，如果两个提交具有相同的控制流结构且变量之间存在双射关系，CLARA 将它们放入同一个聚类。TipsC 首先将程序归一化为线性表示，然后根据 Levenshtein 编辑距离的变体对"相似"程序进行聚类。与 CLARA 和 TipsC 不同，MistakeBrowser 首先学习代码转换（即代码编辑）以纠正错误的提交，然后使用学习到的转换来聚类错误的提交。

OverCode 是一个用于大规模可视化和探索编程提交变体的系统。在聚类提交时，OverCode 首先通过重命名在两个或多个程序跟踪中具有相同序列的公共变量来生成程序的清理代码，然后将清理代码包含相同程序语句集的提交进行分组。

PaCon 与 CLARA、MistakeBrowser、TipsC 和 OverCode 的区别主要在于设计目标。PaCon 旨在帮助教师识别功能正确的提交中的策略，而上述聚类方法旨在为错误的提交生成反馈或可视化提交中的变体。由于这些差异，PaCon 更关注程序的语义特征，而 CLARA、MistakeBrowser、TipsC 和 OverCode 主要考虑语法特征。

SolMiner 利用静态程序分析、数据挖掘和机器学习，从大量提交中挖掘不同的解决方案（具有不同的数据结构、时空复杂度等）。鉴于 SolMiner 将程序表示为一系列微型 AST（每个对应于程序中基本块的一部分），SolMiner 对提交中语法差异的鲁棒性不如 PaCon 。

SemCluster 根据向量表示对提交（无论正确或错误）进行聚类。该向量由两个定量语义特征组成：控制流特征和数据流特征。给定程序和测试套件，控制流特征跟踪流经与不同测试相同控制流路径的输入值数量，而数据流特征跟踪内存中特定值更改为另一特定值的次数。为了计算控制流特征（涉及模型计数），SemCluster 要求教师提供输入值的边界，而 PaCon 没有此要求。此外，SemCluster 利用基于提交间定量语义特征相似性的经典聚类算法，而 PaCon 是在 Z3 约束求解器的帮助下，基于提交间路径条件语义的等价性进行聚类。

Grasa 旨在用最小的生成测试集扩充给定的测试套件，其目的是检测最大数量的错误提交。与 PaCon 不同，为了实现这一目标，Grasa 通过近似彼此的行为等价性来聚类错误的提交。

7. 结论

在本文中，我们唤起了对识别编程提交中不同解题方法（称为策略）的关注，并提出了一种名为 PaCon 的符号分析方法，用于对功能正确的编程提交进行聚类，以提供一种识别策略的途径。与现有的基于语法的方法不同，PaCon 通过路径条件的语义等价性来确定程序的语义等价性。我们在真实数据集上的评估结果表明，PaCon 能够生成数量合理的聚类，每个聚类都能有效地将那些语法多样性高但共享等效路径条件语义的提交归为一组，从而为策略识别提供了一种有前景的方法。

BibTeX

@inproceedings{10.1145/3484272.3484963,

author = {Fu, Yingjie and Osei-Owusu, Jonathan and Astorga, Angello and Zhao, Zirui Neil and Zhang, Wei and Xie, Tao},

title = {PaCon: a symbolic analysis approach for tactic-oriented clustering of programming submissions},

year = {2021},

isbn = {9781450390897},

publisher = {Association for Computing Machinery},

address = {New York, NY, USA},

url = {https://doi.org/10.1145/3484272.3484963},

doi = {10.1145/3484272.3484963},

abstract = {Enrollment in programming courses increasingly surges. To maintain the quality of education in programming courses, instructors need ways to understand the performance of students and give feedback accordingly at scale. For example, it is important for instructors to identify different problem-solving ways (named as tactics in this paper) used in programming submissions. However, because there exist many abstraction levels of tactics and high implementation diversity of the same tactic, it is challenging and time-consuming for instructors to manually tackle the task of tactic identification. Toward this task, we propose PaCon, a symbolic analysis approach for clustering functionally correct programming submissions to provide a way of identifying tactics. In particular, PaCon clusters submissions according to path conditions, a semantic feature of programs. Because of the focus on program semantics, PaCon does not struggle with the issue of an excessive number of clusters caused by subtle syntactic differences between submissions. Our experimental results on real-world data sets show that PaCon can produce a reasonable number of clusters each of which effectively groups together those submissions with high syntax diversity while sharing equivalent path-condition-based semantics, providing a promising way toward identifying tactics.},

booktitle = {Proceedings of the 2021 ACM SIGPLAN International Symposium on SPLASH-E},

pages = {32--42},

numpages = {11},

keywords = {symbolic analysis, programming education, path condition, clustering},

location = {Chicago, IL, USA},

series = {SPLASH-E 2021}

}