二叉树深度解析：从基础结构到实战应用

二叉树深度解析：从基础结构到实战应用

在计算机科学的知识体系中，二叉树就像一把万能钥匙，打开了非线性数据结构的大门。它不仅是理解更复杂树结构（如红黑树）的基础，更在搜索引擎、数据库索引等领域有着广泛应用。本文将基于学习笔记与代码实现，系统梳理二叉树的核心知识，带你从理论到实践全面掌握这一重要数据结构。

一、树与二叉树的概念体系

树结构的核心要素

数据结构中的树完美复刻了自然界树的形态特征，但其概念有着严格的数学定义：

• 根节点：唯一没有父节点的节点（如树干的根基）
• 父节点与子节点：通过边连接的上下级关系（如树枝分叉）
• 叶子节点：没有子节点的节点（如树的叶片）
• 路径：从一个节点到另一个节点的边的序列（如从树根到某片叶子的枝干）

树的关键度量指标：

• 层次：根为第一层，每向下一层递增 1（体现纵向深度）
• 高度：从节点到最深叶子节点的边数（叶子节点高度为 0，空树高度为 - 1）
• 度：节点拥有的子节点数量（叶子节点度为 0，根节点度可大于 2）

二叉树的递归本质

二叉树的定义充满递归之美，理解这一点是掌握其操作的关键：

1. 空树是二叉树
2. 非空二叉树由根节点、左子树、右子树组成，且左、右子树均为二叉树

重要区分：二叉树≠度为 2 的树。其核心差异在于：

• 二叉树的左右子树有严格顺序（左≠右）
• 度为 2 的树要求每个节点最多有 2 个子树，但未规定顺序
• 二叉树允许单个子节点（如只有左子树或只有右子树）
• 空树也是二叉树

二、二叉树的节点定义与构建艺术

节点的代码实现

二叉树节点需存储数据及左右子树引用，JavaScript 中存在两种经典定义方式：

1. 构造函数模式：

javascript

function TreeNode(val) {
    this.val = val;
    // 执行的时候是从右到左的
    this.left = this.right = null; 
}

const root = new TreeNode(1);
const node2 = new TreeNode(2);
const node3 = new TreeNode(3);
root.left = node2;
root.right = node3;
const node4 = new TreeNode(1);
const node5 = new TreeNode(1);
node2.left = node4;
node2.right = node5;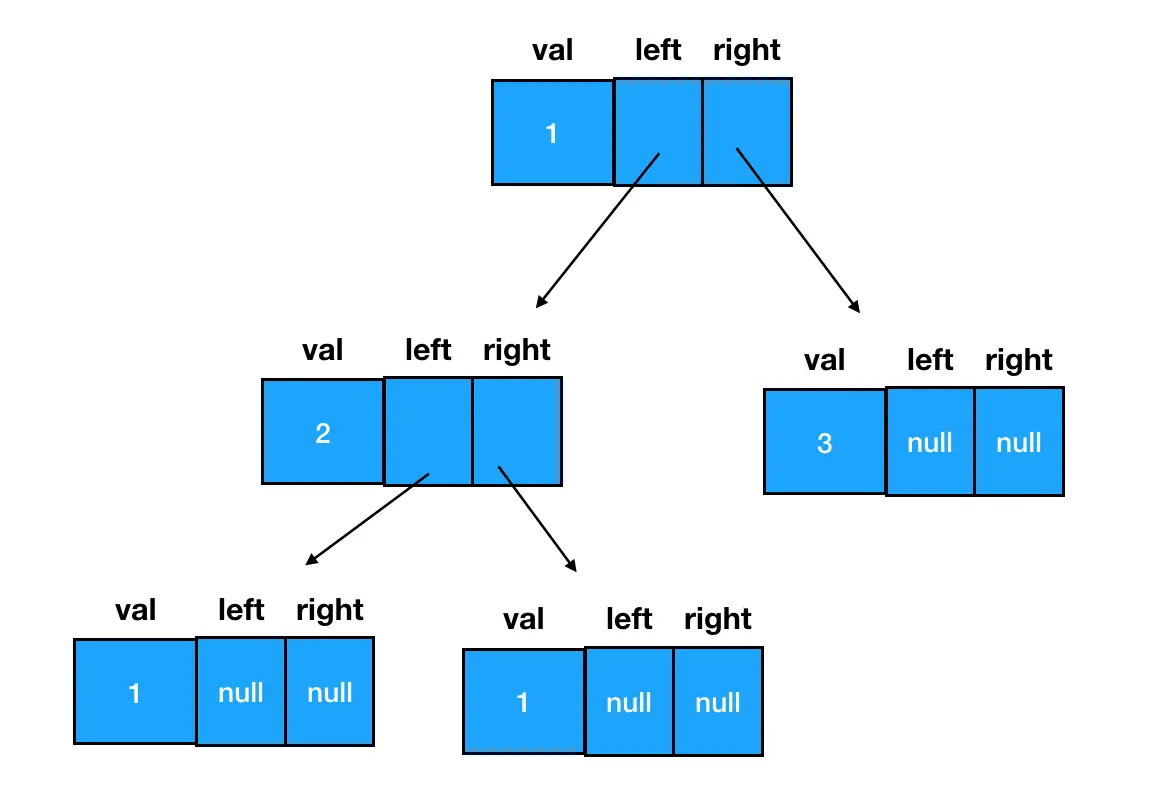

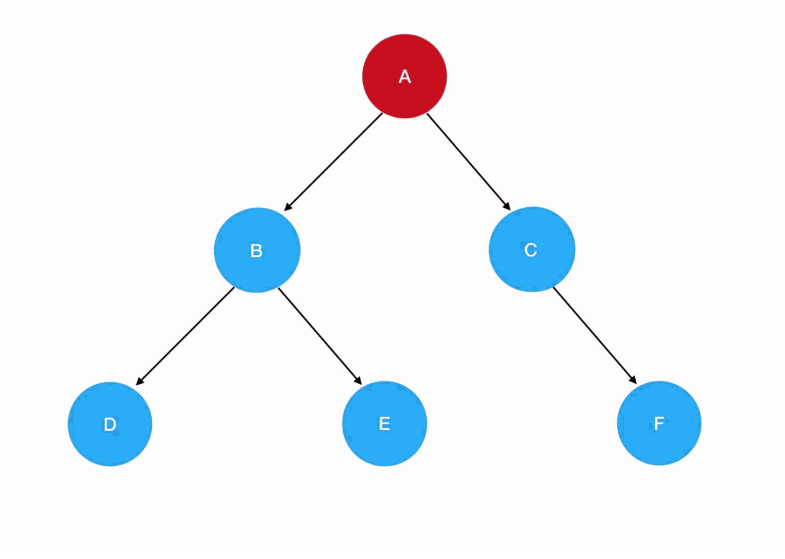
2. 对象字面量模式：

javascript

const tree = {
    val: 'A',
    left: {
        val: 'B',
        left: { val: 'D' },
        right: { val: 'E' }
    },
    right: {
        val: 'C',
        right: { val: 'F' }
    }
};

两种方式各有优劣：构造函数适合动态创建节点，对象字面量适合静态展示树结构，便于调试和可视化。

特殊二叉树的构建

实际应用中常遇到以下特殊二叉树，其构建逻辑值得关注：

• 满二叉树：所有叶子节点在同一层，且非叶子节点均有两个子节点
• 完全二叉树：除最后一层外均满，最后一层节点靠左排列
• 二叉搜索树（BST） ：左子树所有节点值＜根节点值＜右子树所有节点值

例如构建一棵二叉搜索树：

javascript

function buildBST(arr) {
    if (!arr.length) return null;
    const root = new TreeNode(arr[0]);
    for (let i = 1; i < arr.length; i++) {
        let current = root;
        while (true) {
            if (arr[i] < current.val) {
                if (!current.left) {
                    current.left = new TreeNode(arr[i]);
                    break;
                }
                current = current.left;
            } else {
                if (!current.right) {
                    current.right = new TreeNode(arr[i]);
                    break;
                }
                current = current.right;
            }
        }
    }
    return root;
}



// 定义二叉树节点构造函数（buildBST依赖此函数）
function TreeNode(val) {
    this.val = val;
    this.left = this.right = null;
}

// 3. 测试示例：用数组[5,3,7,2,4,6,8]构建BST
const testArr = [5, 3, 7, 2, 4, 6, 8];
const bstRoot = buildBST(testArr);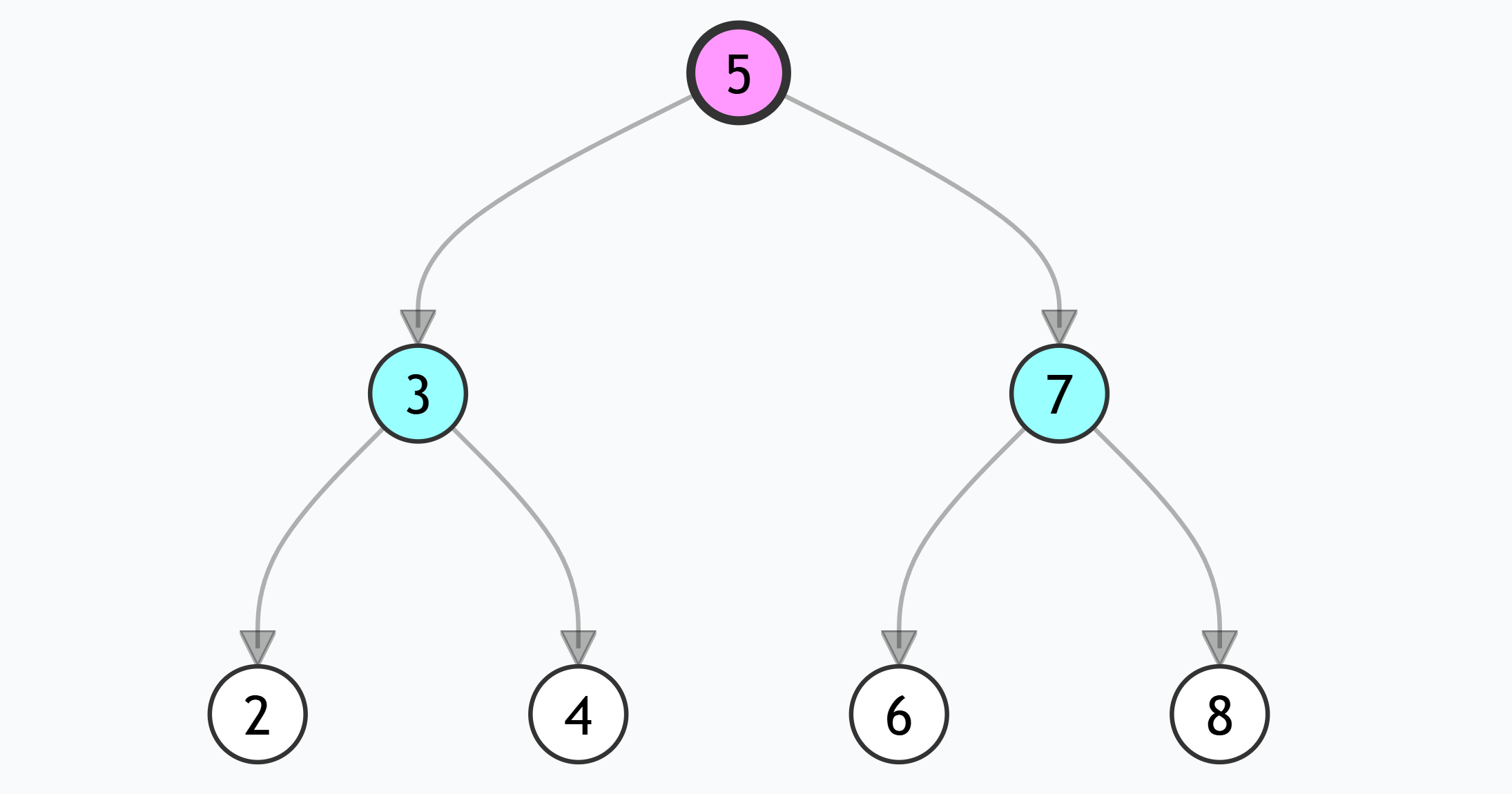

三、遍历算法：探索二叉树的四种路径

遍历的本质是按规则访问所有节点，二叉树的四种遍历方式各有适用场景，其核心差异在于根节点的访问时机。

1. 前序遍历（根→左→右）

先访问根节点，再递归遍历左右子树：

javascript

function preOrder(root) {
    if (!root) return;
    console.log(root.val); // 根
    preOrder(root.left);  // 左
    preOrder(root.right); // 右
}

2. 中序遍历（左→根→右）

先遍历左子树，再访问根节点，最后遍历右子树：

javascript

function inorder(root) {
    if (!root) return;
    inorder(root.left);   // 左
    console.log(root.val); // 根
    inorder(root.right);  // 右
}

3. 后序遍历（左→右→根）

最后访问根节点，先完成左右子树遍历：

javascript

function postorder(root) {
    if (!root) return;
    postorder(root.left);  // 左
    postorder(root.right); // 右
    console.log(root.val); // 根
}

4. 层序遍历（按层次访问，借助队列实现）

借助队列实现，从上到下、从左到右访问节点：

javascript

/**
 * 二叉树层序遍历（借助队列实现）
 */
function levelOrder(root) {
    // 边界处理：空树直接返回空数组
    if (!root) return [];
    
    // 1. 初始化结果数组（存储遍历结果）和队列（核心工具）
    const result = [];
    const queue = [root]; // 第一步：根节点入队
    
    // 2. 循环处理队列：队列不为空则继续
    while (queue.length > 0) {
        // 3. 出队：取出队列头部节点（当前层的第一个节点）
        const currentNode = queue.shift(); 
        // 访问节点：将值存入结果数组
        result.push(currentNode.val);
        
        // 4. 入队：左子节点先入队，再右子节点（保证同一层左→右）
        if (currentNode.left) {
            queue.push(currentNode.left);
        }
        if (currentNode.right) {
            queue.push(currentNode.right);
        }
    }
    
    return result;
}

// 测试示例（构建前文的示例树）
const tree = {
    val: 'A',
    left: { val: 'B', left: { val: 'D' }, right: { val: 'E' } },
    right: { val: 'C', right: { val: 'F' } }
};

// 执行遍历，输出：["A", "B", "C", "D", "E", "F"]
console.log(levelOrder(tree));

非递归遍历实现

递归虽简洁，但可能引发栈溢出，实际开发中常用栈模拟递归：

非递归前序遍历：

javascript

function preOrderIterative(root) {
    if (!root) return;
    const stack = [root];
    while (stack.length) {
        const node = stack.pop();
        console.log(node.val);
        // 右子树先入栈（栈是LIFO）
        if (node.right) stack.push(node.right);
        if (node.left) stack.push(node.left);
    }
}

四、二叉树的重要性质与应用

核心数学性质

1. 非空二叉树中，叶子节点数 = 度为 2 的节点数 + 1
2. 第 k 层最多有 2^(k-1) 个节点（k≥1）
3. 高度为 h 的二叉树最多有 2^h - 1 个节点（满二叉树）

实际应用场景

• 表达式树：用于解析数学表达式（前序遍历得前缀表达式，后序得后缀表达式）
• Huffman 编码：通过哈夫曼树实现数据压缩，叶子节点为字符，路径表示编码
• 决策树：机器学习中用于分类决策，每个节点代表一次判断

五、学习二叉树的实践建议

1. 可视化辅助：画树分析遍历过程，推荐使用在线工具（如 Visualgo）动态演示
2. 代码调试：在遍历函数中添加日志，观察节点访问顺序
3. 问题练习：尝试解决经典问题（如求树的深度、对称二叉树判断、路径总和）
4. 变种扩展：学习二叉搜索树、平衡二叉树等进阶结构，理解其与基础二叉树的联系

二叉树的魅力在于其递归结构与算法思维的完美结合。从简单的节点定义到复杂的遍历策略，每一步学习都是对逻辑思维的锻炼。当你能自如地在树的节点间穿梭时，便掌握了处理非线性问题的核心能力。