数据(逻辑)结构
在计算机科学中,数据的逻辑结构是指数据对象中数据元素之间的相互关系(这里说的数据元素之间的关系是指元素之间本身固有的逻辑关系, 与计算机无关)。
逻辑结构与数据元素本身的形式、内容、相对位置、个数无关。
一些表面上很不相同的数据可以有相同的逻辑结构。
通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着不仅数据元素所包含的数据项的个数要相同,而且对应数据项的类型要一致。
逻辑结构主要包括四种基本关系:集合结构、线性结构、树结构和图结构。
数据(Data):用于描述客观事物的数值、字符等一切可以输入到计算机中,并由计算机加工处理的符号集合。
数据元素(Data Element):数据中的一个个个体,是数据的基本单位。
数据项(Data Item):构成数据元素的成份,是数据不可分割的最小单位。
数据对象(Data Object):具有相同特性的数据元素的一个集合,是数据的子集。
结构(Structure):数据元素之间的关系。
数据结构(Data Structure):相互之间存在一种或多种特定关系的数据元素的集合, 即带结构的数据元素的集合 。
数据结构=数据+结构。
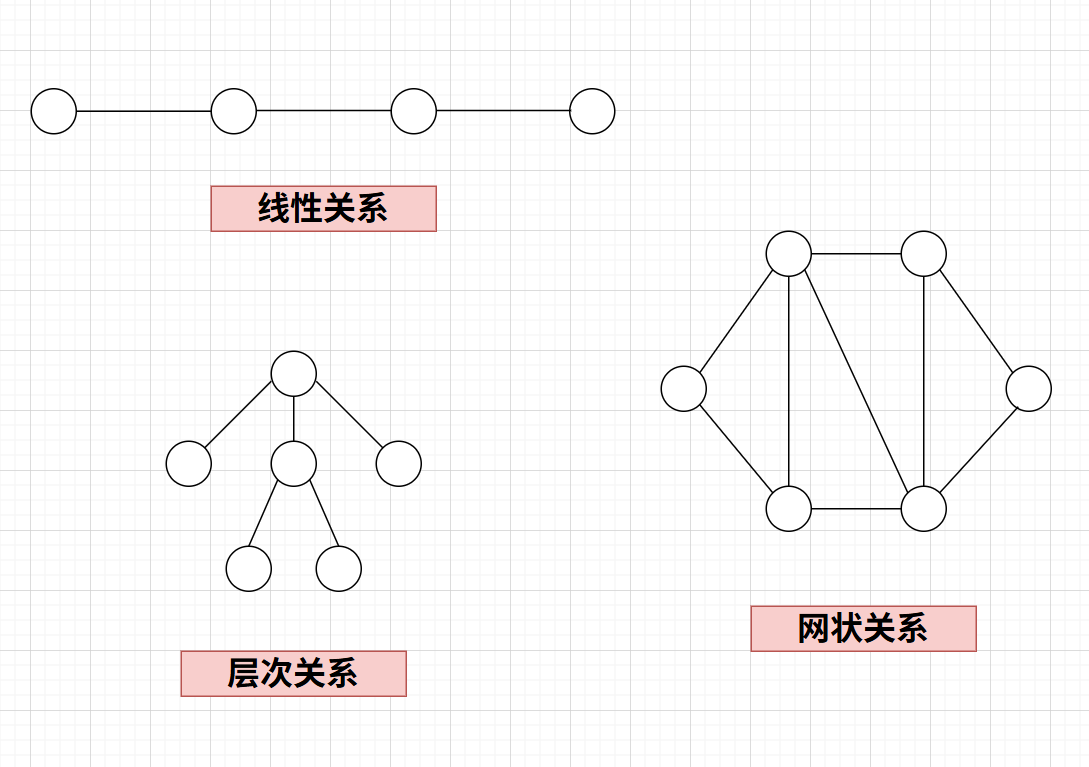
数据元素之间的逻辑关系分为:
(1)线性关系:唯一前驱、唯一后继(满足全序性和单索性);
(2)非线性关系:
①层次关系:唯一前驱、多个后继;
②网状关系:多个前驱、多个后继。
非线性数据结构的种类有:树结构、图结构、堆结构、散列表(哈希表)等。
线性结构的种类有:线性表(如数组、链表等)、栈(后进先出)、队列(先进先出)、双队列(可两端进行插入和删除操作)、串(即一维数组,用于表示字符串)
存储(物理)结构
数据的存储结构:数据结构在计算机中的表示(映象),即数据结构在计算机中的组织形式。又称为数据的物理结构。
数据结构的物理结构是指逻辑结构的存储镜像(image)。
存储结构是数据结构在计算机(内存)中的实现!
我们研究数据结构的目的是要利用数据之间的关系(结构),因此,在存储时既要存储元素本身,还要存储(表示)关系!
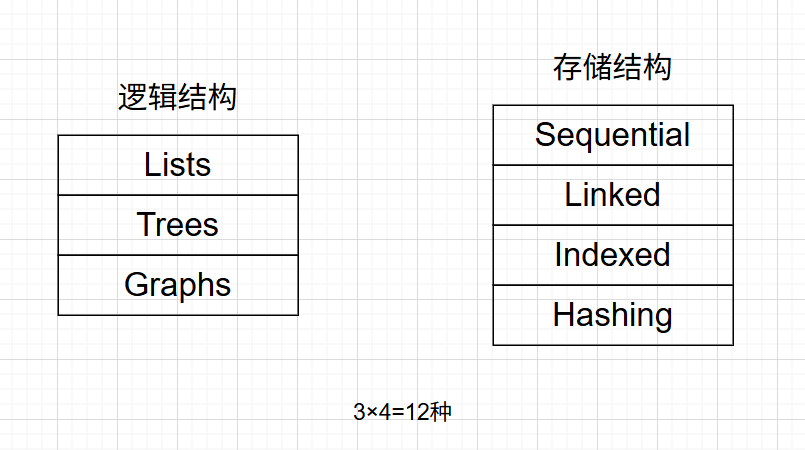
数据结构的物理结构的四种基本映射模型:顺序(Sequential)、链接(Linked)、索引(Indexed)、散列(Hashing)。
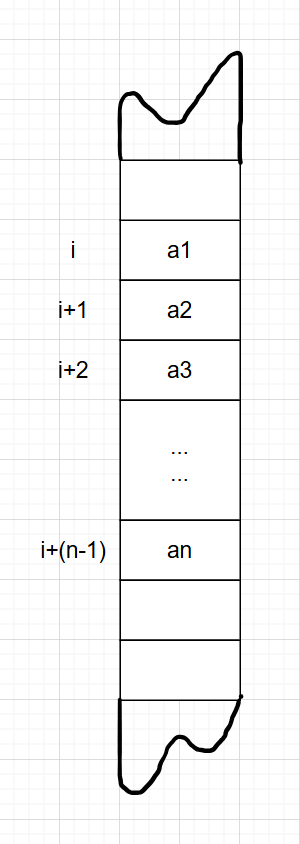
顺序映射:占用连续地址 空间,数据元素依次存放。用物理上的相邻映射出逻辑上的关系(结构);
优点:占用空间少(没有"显式"存储关系);空间连续(地址计算容易)。
缺点:表示关系的能力弱;逻辑上关系发生改变时,必须物理上要调整。
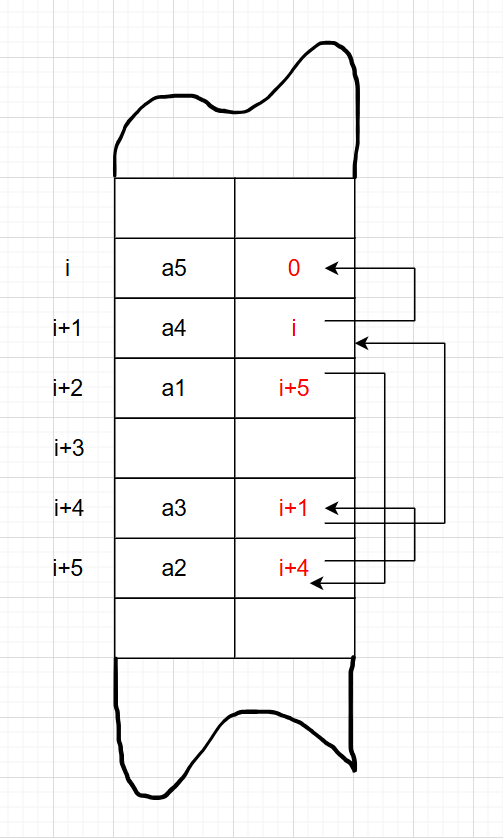
链式映射:占用空间任意,元素任意存放。在存放元素的同时,还存放与其 有关系的元素的地址(指针),即通过指针映射出逻辑上的关系;
优点:空间任意; 显式地存储关系; 表示关系的能力强。
缺点:占用空间较多。
逻辑结构与存储结构的关系
数据的逻辑结构与存储结构之间是抽象与实现的关系:逻辑结构描述数据元素之间的逻辑关系,是独立于计算机的抽象模型;存储结构则是逻辑结构在计算机内存中的具体实现方式,依赖于计算机的物理存储。同一逻辑结构可以采用不同的存储结构来实现。
给定三种逻辑结构(线性、图、树)和四种存储结构(索引、顺序、链接、散列),它们可以相互组合,共形成 3×4=12 种不同的数据结构实现方式,即一共能组成12种不同的数据结构。
注:同一逻辑结构采用不同的关系映射方式,可以得到不同的存储结构。选择何种存储结构来存储相应的逻辑结构,具体问题具体分析,主要考虑数据处理时的占用空间及时间两个因素!
抽象数据类型 Abstract Data Type, ADT
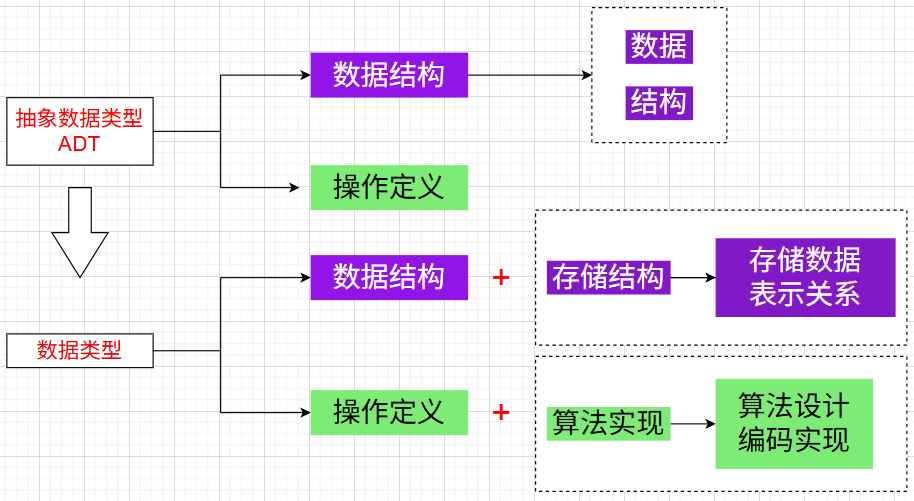
定义:一个++数学模型++ 及定义在这个模型上的++一组操作(或运算)++的总称。
抽象数据类型 = 数学模型 + 操作
= 数据结构 + 操作
=(数据+结构)+ 操作
"抽象"就是"不具体",即数据对象集和操作集的描述与机器无关、与数据存储的物理结构无关、与实现操作的算法和编程语言均无关。简而言之,抽象数据类型只描述++数据对象集++ 和++相关操作集++ "是什么",并不涉及"如何做到"的问题。
数据类型 Data Type
定义:一个数据值的集合和定义在这个值集上的一组操作的总称。
值的集合:这种类型的数据的取值(变量、常量)。 存储(结构) 确定后,值得集合就确定了。
例如:int, 4个字节存储;char,1个字节存储。
一组操作:这种类型的数据的可以参加的运算。 各个操作已经实现 了,直接调用。
例如:int的+,-,++,--,*,/,%;char的+,-。
通常用的数据类型是实现了的抽象数据类型!
抽象数据类型与数据类型
算法基础
算法 Algorithm:(利用某种计算模型)解决问题的一种方法或过程,即操作的具体实现步骤,目的是将给定的输入数据变换为输出结果数据。例如:查找、排序、求最值,......
算法特性:(1)有穷性/终止性:有限步内必须停止; (2)确定性:每一步都是严格定义和确定的动作; (3)能行性:每一个动作都能够被精确地机械执行; (4)输入:满足给定约束条件的输入(可以没有); (5)输出:满足给定约束条件的结果(必须有); ..................
Q:算法与程序的关系?
A:算法是程序的灵魂,程序是算法的肉体。
算法是为了解决一个特定问题而定义的一系列清晰、明确、有限的步骤或指令的集合。
程序 :程序是使用某种编程语言 ,按照特定的语法规则,将算法(可能包含数据结构和处理逻辑)具体编写出来的代码集合。
程序 = 算法 + 数据结构 + 编程语言 + 系统环境与工程细节。
算法设计:算法设计是求解问题的关键,也是软件的核心。这是人的脑力创新的一种表现形式。算法设计是一种艺术。但人们长期设计算法已总结出了一些算法设计策略:
最朴素的策略:蛮力(暴力)
高级策略:分治策略、贪心策略、动态规划策略、回溯策略、智能策略、随机策略、......
蛮力策略基本思想: 该策略直接基于问题的描述和所涉及的概念定义去求解问题。是一种简单直接地解决问题的方法,也是一种最容易应用的算法设计策略。
蛮力策略的特点:适应范围广、易理解、正确性容易证明、效率一般不高(适合小规模)。
典型的蛮力策略算法:顺序查找、简单选择排序、求最值、字符串匹配、矩阵乘法......
分治策略的基本思想:"小问题总是容易解决的!"将一个难以直接解决的大问题,分割成一些规模较小的相同子问题, 以便各个击破,分而治之。

分治策略算法的基本框架:

分治策略算法设计算法的关键(难点):分解、合并。
典型分治策略解决的问题及算法:
查找问题------二分(折半)查找。
排序问题------归并排序。
排序问题------快速排序。
矩阵乘法------Strassen算法。
分治eg:归并排序。
给一个乱序数组
[38, 27, 43, 3, 9, 82, 10]排序。暴力方法(比如冒泡排序)需要挨个比较,效率是O(n²),当数组很大时非常慢。归并排序的做法是:
分解阶段,不停地把数组从中间切分成两半,直到每个子数组只剩一个元素(一个元素自然就是有序的)。这只是准备工作。
真正的魔法和关键在合并阶段 。合并不是简单拼回去,而是进行一个叫"归并"的操作:你现在有两个已经各自排好序的小数组,比如
[27, 38]和[3, 43]。你可以像两叠正面朝上的扑克牌一样,每次都只看两个数组最前面的那个元素,把更小的那个(3)拿出来放到结果里。然后继续比较剩下的最前面元素(27和43),再把小的(27)拿出来。这样,你只需要线性地扫描一遍,就能把两个有序数组合并成一个更大的有序数组。这个合并操作非常高效。整个过程是:先递归地切分到最小单元(分解),然后从最底层开始,一边回溯一边用这种高效的方法合并有序子数组(合并)。最终,所有小有序数组合并成了完整的有序数组。它的效率是O(n log n),比暴力的O(n²)好得多。在这个例子里,分解是手段,合并才是体现智慧、提升效率的核心。没有这个巧妙的合并,分治就失去了意义。
附一份归并排序模板:
cpp#include<iostream> using namespace std; const int N=1e6+10; int n; int q[N],tmp[N]; void merge_sort(int q[],int l,int r){ if(l>=r)return; int mid=l+r>>1; merge_sort(q,l,mid),merge_sort(q,mid+1,r); int k=0,i=l,j=mid+1; while(i<=mid&&j<=r){ if(q[i]<=q[j])tmp[k++]=q[i++]; else tmp[k++]=q[j++]; } while(i<=mid)tmp[k++]=q[i++]; while(j<=r)tmp[k++]=q[j++]; for(i=l,j=0;i<=r;i++,j++)q[i]=tmp[j]; } int main(){ scanf("%d",&n); for(int i=0;i<n;i++)scanf("%d",&q[i]); merge_sort(q,0,n-1); for(int i=0;i<n;i++)printf("%d ",q[i]); return 0; }
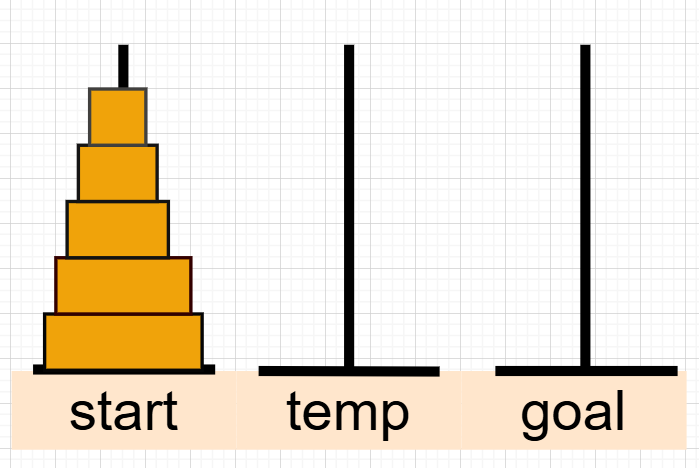
分治eg:汉诺塔移动。
在一块铜板装置上,有三根杆(编号start、goal、temp),在 start杆自下而上、由大到小按顺序放置n个金盘。现要求设计算法,把start杆上的 金盘全部移到goal杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘 子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子 可以置于start、goal、temp任一杆上。
附该题相关代码:
cpp#include<iostream> using namespace std; int n; void Hanoi_Move(int n,char start,char goal,char temp){ if(n==1)printf("%c-->%c\n",start,goal); else{ Hanoi_Move(n-1,start,temp,goal); printf("%c-->%c\n",start,goal); Hanoi_Move(n-1,temp,goal,start); } } int main(){ scanf("%d",&n); char start,goal,temp; start='A',goal='C',temp='B'; Hanoi_Move(n,start,goal,temp); return 0; }
最优化问题(optimization problem):即求最优解问题。每个最优化问题都包含一组限制条件(constraint)和一个优化函数(optimization function)。
贪心策略:贪心策略是通过"分步决策"的方法来求解问题的,它在求解问题的每一步上依据"某种准则"做出当前看来最好的决策,产生n-元组解的各个分量。
贪心策略的基本思想:首先选定一种最优量度标准(贪心准则),作为选择当前分量值的依据。然后依据该标准,在每一步上做出当前最好的选择,最终每一步的最优决策正好构成问题的最优解。即,局部贪心得到全局最优!
贪心准则考虑的是局部最优性。
贪心策略设计算法的基本步骤:
(1)确定问题的可行解的求解方法,即满足约束条件的解;
(2)根据问题的贪心性质,确定贪心准则(局部最优的原则)(关键);
(3)应用贪心准则,得到目前的局部最优解;
(4)简化原问题使之成为简单一些的子问题;
(5)自顶向下,以迭代的方式作出相继的贪心选择,直到问题的最优解得到。
(6)证明算法的正确性(关键)
用贪心策略解决的典型问题及算法:最少个数找零、装载(背包问题等)、活动安排问题、最短路径问题的Dijkstra算法、哈夫曼树(最优二叉树)生成算法、最小连通代价问题的最小生成树算法(Prim算法,Kuskal算法)。
贪心eg:经典的找零问题。
现有6种面值的纸币:1元、5元、10元、20元、50元、100元。输入一个正整数n表示需要找零的金额,请使用贪心策略计算并输出凑出金额n所需的最少纸币数量。
解:
本题贪心策略下,优先使用面值大的纸币。
附代码:
cpp#include<iostream> using namespace std; int n; int main(){ scanf("%d",&n); int denom[]={100,50,20,10,5,1}; int count=0; for(int i=0;i<6;i++){ count+=n/denom[i]; n%=denom[i]; } printf("%d",count); return 0; }面值系统规范的情况下,贪心总能高效得到最优解。
但在面值任意的情况下,贪心不能保证最优,如denom={1,3,4},n=6。这就需要用到接下来的策略------动态规划。
动态规划策略的基本思想:通常也一般用于求解最优化问题,与贪心策略类似,也是通过子问题的最优解求得整个问题的最优解。但是是从全局出发,通过问题分析,挖掘子问题最优解和整个问题最优解的关系,建立动态规划方程。
动态规划策略的关键:
剖析问题具有最优子结构性质;
建立动态规划方程(标准、非标准)(即,刻画出子问题最优解和原问题最优解的关系);
求解动态规划方程(求解过程就是设计的动态规划算法)。
动态规划策略算法的基本框架:
动态规划策略设计的算法就是求解动态规划方程的过程。动态规划方程一般是递归的,通常的求解方式有两种:
自顶向下的递归(+备忘录);
自底向上的递推。
动态规划eg:
硬币面值为 1 元、3 元、4 元,输入一个正整数 n 表示需要凑出的金额,请计算并输出凑出金额 n 所需的最少硬币数量。如果无法凑出,输出 -1。
解:
动态规划思路:
定义状态:dp[i] 表示凑出金额 i 所需的最少硬币数。
状态转移:对于每个金额 i,考虑所有面值 coin,若 i >= coin ,则dp[i]=min( dp[i] , dp[ i - coin ] + 1 ) 。
初始化:dp[0]=0,其余为无穷大。
附代码:
cpp#include<iostream> #include<vector> using namespace std; const int inf=1e6; int n; int main(){ scanf("%d",&n); int coins[]={1,3,4}; vector<int>dp(n+1,inf); dp[0]=0; for(int i=1;i<=n;i++){ for(int j=0;j<3;j++){ if(i>=coins[j]){ dp[i]=min(dp[i],dp[i-coins[j]]+1); } } } if(dp[n]==inf)printf("-1"); else printf("%d",dp[n]); return 0; }
算法设计是难点、重点,更是计算机求解问题的关键和核心!
算法描述:
- 自然语言描述。特点:容易,但有时啰嗦、有二义性。
- 图示(流程图、N-S图、PAD图等)。特点:直观清晰,但不易实现。
- 算法语言(伪代码)。特点:严谨、简洁,易程序实现。
- 程序设计语言。特点:可以直接运行,但太严格。
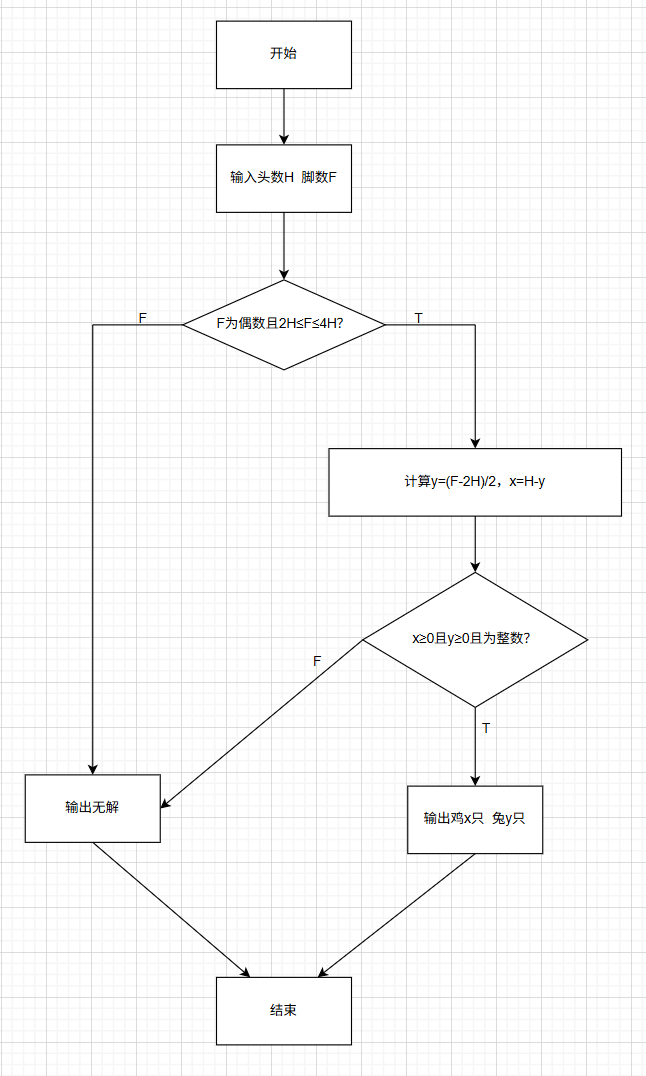
以鸡兔同笼问题,展示以上四种描述方式:
1.自然语言描述:
首先,我们知道每只鸡有1个头和2只脚,每只兔有1个头和4只脚。
设鸡的数量为x,兔的数量为y。
那么可以得到两个方程:
头的总数:x + y = H
脚的总数:2x + 4y = F
解这个方程组:
从第一个方程得:x = H - y
代入第二个方程:2(H - y) + 4y = F
化简:2H - 2y + 4y = F → 2H + 2y = F
所以:y = (F - 2H) / 2
然后:x = H - y
但需要检查解是否合理:F必须是偶数,且F≥2H,F≤4H,结果应为非负整数。
2.图示:
3.算法语言:
BEGIN
IF (F mod 2 ≠ 0) OR (F < 2H) OR (F > 4H) THEN
OUTPUT "无合理解"
RETURN
END IF
y ← (F - 2 * H) / 2
x ← H - y
IF (x ≥ 0) AND (y ≥ 0) AND (x为整数) AND (y为整数) THEN
OUTPUT "鸡有", x, "只,兔有", y, "只"
ELSE
OUTPUT "无整数解"
END IF
END
4.程序设计语言
cpp#include<iostream> using namespace std; int H,F,x,y; int main(){ scanf("%d %d",&H,&F); if(F%2||F<2*H||F>4*H){ printf("无和理解"); return 0; } else{ y=(F-2*H)/2; x=H-y; if(x>=0&&y>=0&&2*x+4*y==F){ printf("鸡有%d只,兔有%d只",x,y); } else printf("无和理解"); } return 0; }
算法评价:
正确性(Correctness):任何输入,都能得到预期的输出。这是一切的前提!
易读性(Readability):易于阅读和理解和让别人看懂。
健壮性(Robustness):不会产生异常或莫名其妙的结果。
有效性(Efficiency):资源的消耗要少。主要是时间、空间资源。
........................
简单性;一般性;有效性。
算法复杂性分析
解决问题(方案)方法的效率:跟数据的组织方式有关(数据结构,如栈、队列、树、.......);跟空间的利用效率有关(存储结构,如顺序、链式、.......);跟算法的巧妙程度有关(算法策略,如蛮力、分治、贪心、....... )。
数据是基础,核心是处理(即算法是处理数据的),因此放率都体现在算法中!
算法分析(AlgorithmAnalysis):分析和评估一个算法效率的方法,包包括++运行时间++效率和++空间++效率(称为算法的复杂性)。
复杂性分析方法:
(1)实验方法:选择样本数据、运行环境、实现并运行算法, 记录和分析占用资源(空间、时间)情况。优点:精确。缺点:可比性差,效率低。
(2)评估方法:根据算法本身的流程和逻辑特征,分析和估算算法运行时占用资源(空间、时间)情况。优缺点与实验方法相反。
评估是人的重要的基本技能之一,也是工程学的内容之一!
评估的一般步骤:
(1)确定问题中与评估目标相关的主要参数;
(2)推导出一个与问题参数有关的公式(模型);
(3)选择参数值,由该公式得出一个评估解。
空间复杂度S(P),一般简化为S(n),参数n是问题的规模。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断(内存溢出)。
时间复杂度T(P),一般简化为T(n)。时间复杂度过高的低效算法可能导致运行时间超限。
有时间会继续补充渐进复杂性分析、时间/空间复杂度计算等。