中级软考（软件工程师）第三章知识点——数据结构与数据运算

蓝桉~MLGT2026-01-12 8:36

中级软考（软件工程师）第三章知识点------数据结构与数据运算

从大纲可以看出大部分都是关于排序和查找，对于有开发经验的同胞们来说理解并不难，只是我们很少将这类知识应用于题目和计算上。

一、线性结构

1. 线性表

1.1 基础定义

  • 定义： 最基本的数据结构，一个线性表是由n（n ≥ 0）个元素的有限集合，通常表示为（ a 1 , 1 2 , . . . , a n a_1, 1_2, ... ,a_n a1,12,...,an）。
  • 特点：
    • 存在唯一的一个称作"第一个"的元素
    • 存在唯一的一个称作"最后一个"的元素
    • 除第一个元素外，序列中每一个元素都有一个"直接前驱"
    • 除最后一个元素外，序列中每一个元素都有一个"直接后继"

1.2 存储结构

（1）顺序存储
  • 定义： 用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的元素在物理上也相邻。
  • 优点： 可以随机存取表中的元素。
  • 缺点： 插入与删除都需要移动元素。
  • 常用公式： 假设第一个元素 a 1 a_1 a1的内存地址是 L O C ( a 1 ) LOC(a_1) LOC(a1)，每个元素占 L L L个字节，问第 i i i个元素 a i a_i ai的地址是多少？
    L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) x L LOC(a_i)=LOC(a_1)+(i-1)xL LOC(ai)=LOC(a1)+(i−1)xL

这个公式比较好理解，用第一个元素的地址加上除去第一个元素的地址之和即可

（2）链式存储
  • 定义： 链式存储通过指针的链接的节点存储数据元素，也就是在物理意义上并不连续。
  • 分类： 单链表，只能存头结点开始顺序遍历整个链表，循环链表（循环单链表、循环双链表），可以从表中的任何一个节点开始遍历整个链表。
  • 优点： 插入与删除都不需要移动元素。
  • 缺点： 不能对数据进行随机访问。
（3）时间复杂度对比
操作类型 顺序表 (数组) 链表 (单链表) 备注
按值查找 O(n) O(n) 无序情况下都要挨个找
按序号查找 (读取) O(1) O(n) 顺序表赢麻了
插入/删除 (已知位置) O(n) O(1) 链表赢麻了
插入/删除 (未知位置) O(n) O(n) 链表虽然改指针快，但找到位置也要花时间

时间复杂度的定义：程序执行次数与数据总量之间的关系。

  • O(1) ：常数阶 ：无论数据量多大，我需要的次数都是固定的，不会循环。
  • O(n) ：线性阶 ：数据量翻倍，耗时也翻倍，一般都需要通过循环实现。

📝 上面这两种是线性表和链表中的时间复杂度，后面还会出现几种，我们提前预热一下

  • O( l o g n log_n logn) ：对数阶 ：典型算法是二分查找，就是对半砍，这样最后算下来的时间复杂度就是 l o g n log_n logn
  • O( n l o g n nlog_n nlogn) ：线性对数阶 ：这是理论上排序算法的极限速度，逻辑是按照分层处理，但是每一层需要处理的元素还是n，所以就是 O ( n ) O(n) O(n)和 O ( l o g n ) O(log_n) O(logn)的时间复杂度之和。（如果纠结这个怎么算出来的可以自行百度，需要用到一些数据知识，鄙人数学比较差）
  • O( n 2 n^2 n2) ：平方阶 ：通常就是两层嵌套循环。
  • O(2^n) ：指数阶：最慢的，一旦出现计算机就挂了。
（4）单链表、双链表，以及对应循环单/双链表的区别

单链表 vs 双链表

比较维度 单链表 双链表
节点结构 `[Data Next]` 只有一个指针，指向后继。
行走方向 单行道。 只能从头走到尾，过了这个村就没这个店。 双向车道。 可以前后反复横跳。
找后继节点 O(1) O(1)
找前驱节点 O(n) 必须从头开始遍历，直到找到 p->next == target。 O(1) 直接访问 p->prior。
删除节点 p O(n) 因为要删除 p，必须修改 p 的前驱节点的 next 指针。单链表找不到前驱，只能重头找。 O(1) 因为 p 自带前驱指针，直接改就行。
空间开销 小 大 (每个节点多存一个指针)

📝 如果研究过Java的数组部分应该对这部分不陌生，我们只需要记着双链表更加适合随意的删除和新增节点 。有兴趣可以看看我的一篇专门讲Java的集合的文章Java集合

循环单链表 vs 循环双链表

📝 "循环"的核心定义是：最后一个节点的 next 指针不指向 NULL，而是指回 Head（头结点）。

比较维度 循环单链表 循环双链表
结构闭环 单向环。 像田径跑道，只能逆时针跑。 双向环。 头的前面是尾，尾的后面是头。
访问尾结点 O(n) (如果有头指针) 必须转一圈才能摸到屁股。 （注：如果专门维护一个尾指针 rear，则是 O(1)） O(1) 直接 head->prior 就是尾结点。这是最大的优势。
遍历终止条件 p->next == head 跑了一圈回到了起点。 p->next == head 或 p->prior == head
容错性 如果链表断裂，后面的节点全部丢失。 即使断了一个方向，还有机会通过反向指针找回（理论上）。

💡 针对考试，主要记着下面这几点

  • 想省空间？ → 单链表。
  • 经常要在"当前节点"的前面搞事情（插/删）？ → 双链表。
  • 需要从任意节点出发都能遍历全表？ → 循环链表。
  • 既要随便遍历，又要快速找前驱，还要快速找首尾？ → 循环双链表（全能王，但费空间）。

2. 栈

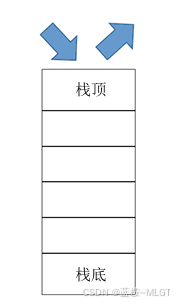
📝 栈就不多说了，核心四个字："后进先出"

考题：有一个栈，输入序列是 1,2,3（按顺序入栈，但中间随时可以出栈），问：下列哪个出栈序列是不可能的？

2.1 栈的应用场景

  1. 递归：通常需要通过栈保存每一层的函数变量和返回值，通常在循环中比较容易遇到的就是栈溢出错误。
  2. 表达式求值
  3. 括号匹配

3. 队列

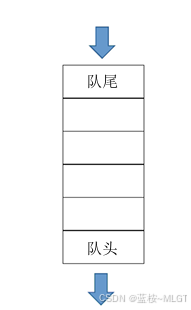
  • 定义： 一种"先进先出 "的线性表，在队列中允许插入元素的一端称为队尾 ，允许删除元素的一端称为队头。

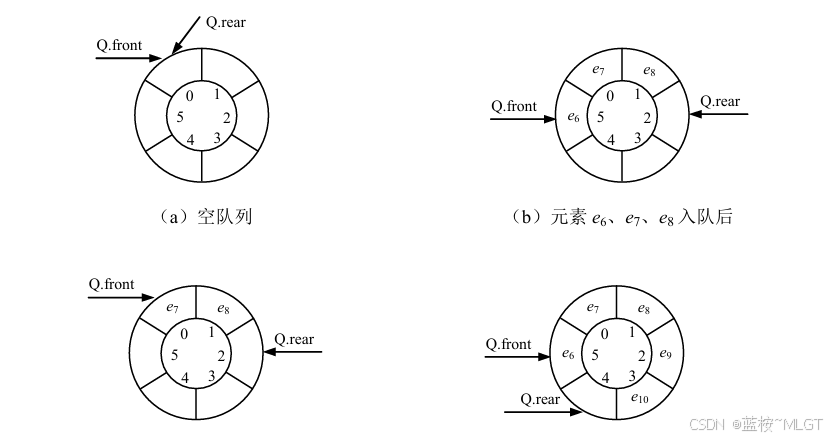
3.1 循环队列

📝 循环队列出现的核心原因是：普通队列的"假溢出"问题，这是重点。



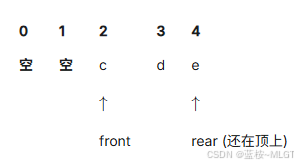
假溢出出现的原因：

分析上面的两种图，第一张是队列满了的情况，第二张是先进入的元素出去了，注意了，此时rear节点并没有改变位置，所以计算机判定还是一个满状态，在插入元素是不是就溢出了呢。

循环队列的解法： 首尾相连！（就不文字解释了，直接上图）

（1）公式一：下标计算

N e x t I n d e x = ( I n d e x + 1 ) 取模 M A X S I Z E NextIndex = (Index + 1) 取模 MAXSIZE NextIndex=(Index+1)取模MAXSIZE

这个公式不难，注意下标加一取模就行了

（2）判空与判满
  • 判空： front == rear，头指针和尾指针相重叠。
  • 判满： 牺牲一个存储单元，如果不牺牲就无法判断了，因为和判空会重复。
  • 公式：
    ( r e a r + 1 ) 取模 M A X S I Z E = = f r o n t (rear + 1) 取模 MAXSIZE == front (rear+1)取模MAXSIZE==front
（3）队列长度

L e n g t h = ( r e a r − f r o n t + M A X S I Z E ) 取模 M A X S I Z E Length = (rear - front + MAXSIZE) 取模 MAXSIZE Length=(rear−front+MAXSIZE)取模MAXSIZE

3.2 双端队列

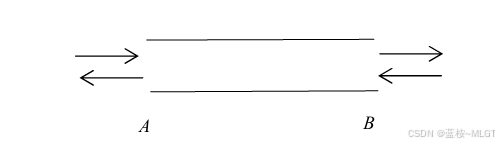
  • 定义： 要求进出队列必须要在同一端口。

双端队列的几种变体

  • 一端进，两端出
    输入序列 1 , 2 , 3 , 4 （从右进）。问：能得到输出序列 4 , 2 , 1 , 3 吗？ 输入序列 1, 2, 3, 4（从右进）。问：能得到输出序列 4, 2, 1, 3 吗？ 输入序列1,2,3,4（从右进）。问：能得到输出序列4,2,1,3吗？
  • 两端进，一端出 ：这种比一般的队列灵活，但是只有一端可以出，所以输出受限，但有一个特点就是可以"插队"，因为你可以直接放在输出端那头。
  • 双栈模拟队列： 就是最开始的图，这种的场景主要是在一块连续的内存中存入两个栈，栈1往右存（地址变大），栈2往左存（地址变小），直到两个栈碰头（溢出）就说明满了，就是Top + 1 == Top2。优势就是非常节省内存，没浪费。
  • 标准双端队列：
    • 结构： 两端随便进，随便出。
    • 能力： 最强，包含了栈和队列的所有功能。

3.3 队列常见应用场景

  • 广度优先搜索（BFS）
  • 缓冲区（Buffer）
  • 操作系统调度（先来先服务FCFS）

3.4 链式队列

📝 这一部分我只能说，背一个代码就行，其它的想了解了解一下，通常在C的填空那儿出现。

c 复制代码 
p = Q.front->next;      // p 指向第一个真实数据
Q.front->next = p->next; // 此时 front 指向了 p 的下一个（可能是NULL）

// 【关键判别】如果删掉的这个节点(p)就是队尾节点(rear)
// 说明删完队列就空了
if (Q.rear == p) {
    Q.rear = Q.front;   // 【必考点】必须把 rear 拉回来指向头结点！
}

free(p);

4. 串

📝 串是一种线性表，一般为 s = " a 1 , a 2 . . . a n " s="a_1,a_2...a_n" s="a1,a2...an"，其中（n > 0）

4.1 空串

  • 定义： 长度为0的串。
  • 符号： ∅ ∅ ∅ 或 ""。
  • 特点： 啥都没有。
  • 考点： 空串是任意串的子串。

注意要区别空格串，空格串的长度不为0，只是内容为空格，但实际还是没有什么意义。

4.2 子串

  • 定义： 主串中任意长度的连续字符序列。
  • 特点： 连续！
  • 子串的计算公式：

子串总数 = n ( n + 1 ) / 2 + 1 ( 最后的 1 是空串 ) 子串总数=n(n+1)/2 + 1(最后的1是空串) 子串总数=n(n+1)/2+1(最后的1是空串)

二、非线性结构

1. 二维数组

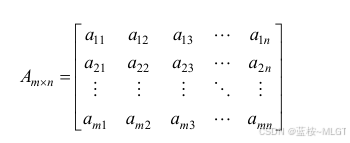
  • 数据元素数目固定。
  • 数据元素具有相同的类型。
  • 数据元素的下标具有上下界约束且下标有序。

这个我们不陌生，唯一需要记住的就是两个计算存储地址的公式。

题目 ：假设每个元素占用L个单元，m和n分别为数组的行数和列数， L o c ( a 11 ) Loc(a_{11}) Loc(a11)表示元素 a 11 a_{11} a11的地址。

  • 以列为主序优先：

L o c ( a i j ) = L o c ( a 11 ) + ( ( j − 1 ) × m + ( i − 1 ) ) × L Loc(a_{ij}) = Loc(a_{11}) + ((j-1) \times m + (i-1)) \times L Loc(aij)=Loc(a11)+((j−1)×m+(i−1))×L

复制代码 
- 公式解析：只需要计算出元素之前跳过了多少个元素，那么以列为朱序
- 我们要先计算跳过了多少列：j-1
- 每一列一共有m行，所以跳过了 (j - 1) * m 个
- 然后当前列还有之前的 i - 1 个，所以这个公式就不攻自破了
  • 以行为主序优先：

L o c ( a i j ) = L o c ( a 11 ) + ( ( i − 1 ) × n + ( j − 1 ) ) × L Loc(a_{ij}) = Loc(a_{11}) + ((i-1) \times n + (j-1)) \times L Loc(aij)=Loc(a11)+((i−1)×n+(j−1))×L

2. 三对角矩阵

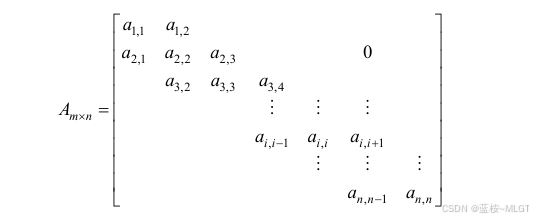
📝 这是一张关于特殊矩阵压缩存储的经典例子，关于这个我们需要理解两个公式，不一定要背。

  • 定义： 中间那条线和上下两条线的数据是非0的，其余都是0。
  • 带状分布： 所有非0元素下标都满足 ∣ i − j ∣ < = 1 |i - j| <= 1 ∣i−j∣<=1

2.1 通过矩阵计算一维数组的下标

2.1 通过一位数组反推三角矩阵的位置

📝 其实这个更复杂，建议是不记公式，直接带入选项计算即可。

i = [ ( k + 1 ) / 3 ] + 1 i = [ (k + 1) / 3] + 1 i=[(k+1)/3]+1

3. 树

⚠️ 这是知识点最多的一小节，也是最常考的。

📝 树是n个（n >= 0）节点的有限集合，有且仅有一个根节点，当n = 0 时称为空树。

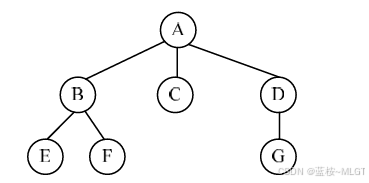
3.1 树的基本概念

  • 双亲、孩子和兄弟：子节点就是一个节点的子树，双亲节点（一般叫父节点）是子树的根节点，兄弟节点就是平级的节点。
  • 节点的度： 一个节点拥有子树（子节点）的个数称为该节点的度。比如图中A的度就是3。
  • 树的度： 树中所有节点度的最大值。
  • 叶子结点： 度为0的节点，没有任何子节点。
  • 内部节点： 排除叶子结点和根节点，其余都是内部节点。
  • 节点的层次： 也就是层级，A是第一层，B、C、D是第二层，依此类推。
  • 树的深度： 最大层数，也可以叫高度。
  • 路径长度： 两个节点之间经过的边的数目。
  • 有序 / 无序 树： 如果子树依次从左到右排序且不能变换位置就是有序树，反之则是无序树。

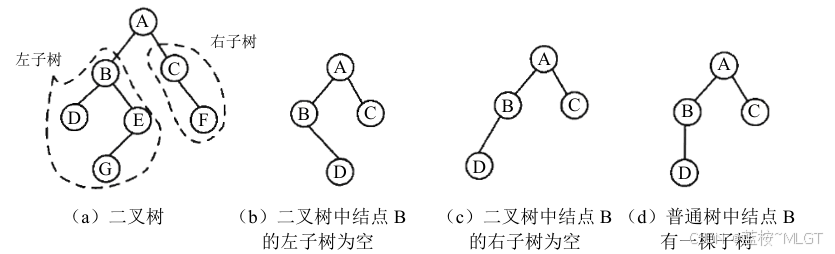
3.2 二叉树

📝 二叉树和普通树的区别在于，二叉树的子树分为左子树和右子树，而普通树只有一颗子树。

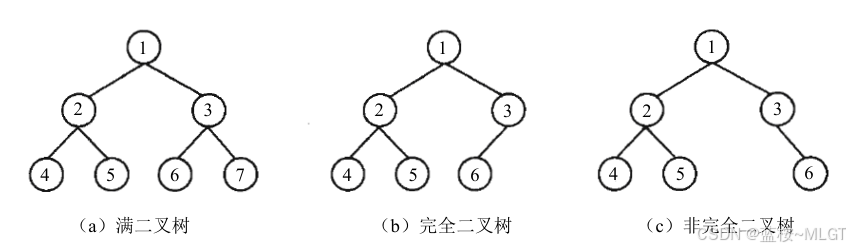
3.3 满二叉树和完全二叉树

📝 记着，满二叉树的节点总数为 2 k − 1 2^k - 1 2k−1

3.4 二叉树的性质

  • 二叉树的第 i i i层上最多有 2 i − 1 2^{i-1} 2i−1个结点（i >= 1）
  • 深度为k的二叉树最多有 2 k − 1 2^k - 1 2k−1个节点 （k >= 1）
  • 对于任何一颗二叉树，如果叶子节点数为 n 0 n_0 n0，度为2的节点数为 n 2 n_2 n2，则 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1（⚠️ 重点）
  • 具有n个结点的万全二叉树的深度为 [ l o g 2 n ] + 1 [log_2n] + 1 [log2n]+1
  • 如果对一颗有n个结点的万全二叉树的节点按照层序编号，则对任一节点i（ 1 < = i < = n 1 <= i <= n 1<=i<=n）有：
    • 如果i = 1，则该节点是二叉树的根，无双亲；如果i > 1，则该节点是 i / 2 i / 2 i/2。
    • 如果2i≤n，则该结点左子树的编号是2i；否则，无左子树。
    • 如果2i+1≤n，则该结点右子树的编号是2i+1；否则，无右子树

3.5 二叉树的存储结构

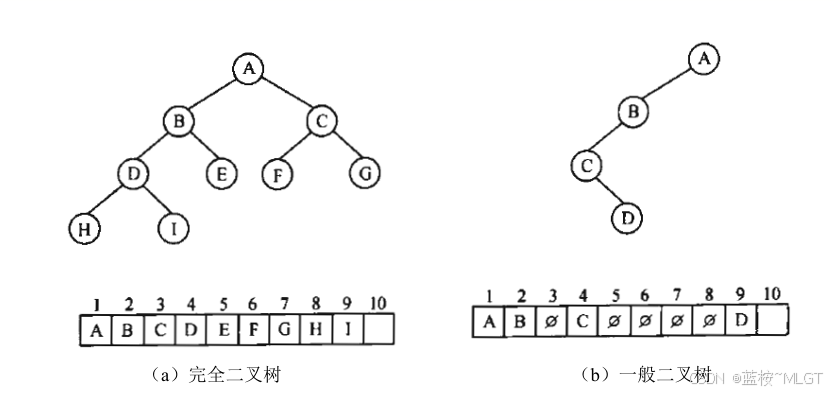
（1）顺序存储

📝 这种存储方式万全二叉树是有优势的，因为节点都是满的，而一般二叉树还需要填充空节点，导致空间浪费。

（2）链式存储

📝 一般分为二叉链表和三叉链表。

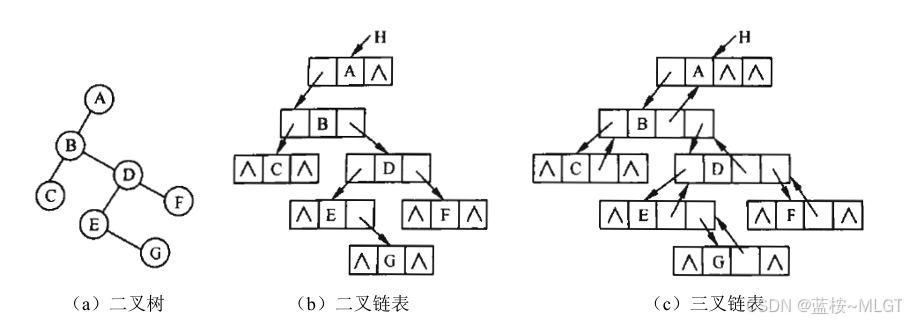
链表

c 复制代码 
struct TreeNode {
    int data;               // 数据域
    struct TreeNode *lchild; // 左指针
    struct TreeNode *rchild; // 右指针
};
  • 空指针问题
    • 具有n个结点的二叉链表中，一共有 2 n 2n 2n个指针域
    • 其中有 n − 1 n - 1 n−1个指针指向了孩子（也就是 n − 1 n - 1 n−1条边）
    • 剩下的 2 n − ( n − 1 ) = n + 1 2n - (n - 1) = n + 1 2n−(n−1)=n+1个空指针域（NULL），线索二叉树就是用这些空指针存放前驱后继信息的（优点类似红黑树）。

3.6 二叉树的遍历

📝 还记得之前说的那个后序遍历吗，这里了解完整的几种遍历方式。

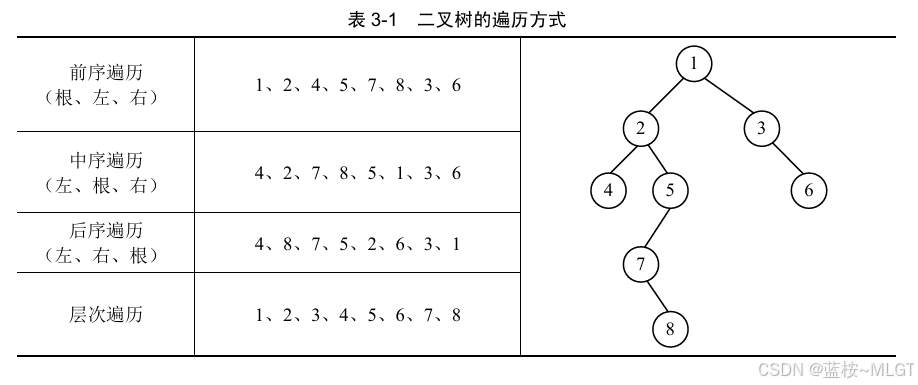
如果忘记怎么遍历的，看下面的线路图，有时候我们不能按照我们视觉上的左中右来理解二叉树，得按照计算机思维，下面用后序遍历来说

3.7 最优二叉树（哈夫曼树）

📝 一种带权路径长度最短的二叉树

  • 路径长度：从树根到每一个结点的路径长度之和。
  • 带权路径长度 (WPL, Weighted Path Length)：结点权值 × 结点到根的距离（层数-1）。
  • 定义：WPL 最小的二叉树就是哈夫曼树。

4. 图

📝 图是由集合 V V V和 E E E构成的二元组，记作 G = ( V , E ) G=(V,E) G=(V,E)，其中 V V V是图中顶点的非空有限集合， E E E是图中边的非空有限集合。

4.1 图的存储结构

（1）邻接矩阵

📝 具体定义就不描述了，比较抽象，我们直接看图理解

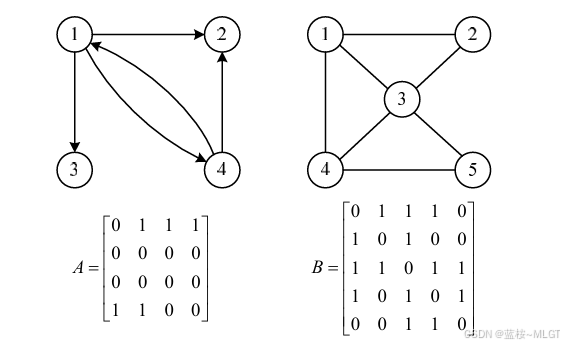
  • 规则：
    • A [ i ] [ j ] = 1 A[i][j] = 1 A[i][j]=1：表示顶点 i i i到顶点 j j j有边。
    • A [ i ] [ j ] = 0 A[i][j] = 0 A[i][j]=0：表示没边。

拿矩阵A来说，第一个元素是11，没有边，第二个是12，表示1------2，看图是有边的，依此类推即可。

  • 无向图 ：矩阵是对称的，第 i i i行的所有元素之和 = 顶点 i i i的度。（度就是有几根线）
  • 有向图 ：不一定对称，出度 看行，也就是看对应的顶点射出去了几根线。入度看列，看顶点被射中了几次。
  • 优点： 查询很快，直接看矩阵对应的值即可，时间复杂度 O ( 1 ) O(1) O(1)
  • 缺点： 费空间，咋滴都得有一个 N x N N x N NxN的矩阵
（2）邻接表

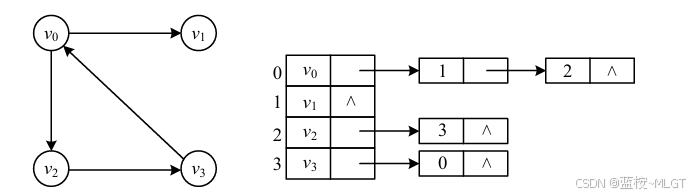
📝 采用数组+链表的形式，数组存储所有的节点，链表存储出度的节点，相当于边。

  • 优点：
    • 节省空间： 有多少边就申请多少空间，适合稀疏图
    • 计算出度快： 直接遍历对应节点的链表即可
  • 缺点：
    • 计算出度稍微慢一点，要遍历整个链表，不像矩阵直接计算和即可。
    • 计算入度相当慢，需要把所有的链表遍历，除非维护一个逆向邻接表。

邻接矩阵和邻接表是典型的空间和时间的案例，用空间换时间，或者用时间换空间。

4.2 图的遍历

  • 深度优先（DFS）： 类似树的前序遍历
  • 广度优先（BFS）： 类似树的层次遍历
场景特征 选哪个算法？ 为什么？
求最短路径、最少步数 BFS (广度) 它是一圈圈扩散的，最先摸到的目标肯定最近。
求这一步之后有多少种可能 DFS (深度) 它适合把一种可能性走到黑，不行再换一种。
判断两个点连不连通 DFS/BFS 都可以 只要能走到就行，无所谓远近。但写 DFS 代码（递归）通常更短更简单。
社交网络好友推荐 BFS (广度) 由近及远，先找一度好友，再找二度好友。
解决数独、八皇后问题 DFS (深度) 需要尝试放一个数字，如果不冲突就继续放下一个，冲突了就回退（回溯）。

三、数据运算

1. 查找

1.1 顺序查找

  • 定义：最基础的查找方式，从头到尾一个一个比对。
  • 核心原理：暴力遍历。不管数据有没有顺序，挨个问："你是那个数吗？"
  • 时间复杂度 ： O ( n ) O(n) O(n) （最坏情况要找遍所有人）。
  • 优点：算法简单，对数据没有任何要求（有序无序皆可），适合链表。
  • 缺点：效率低，数据量大时非常慢。
  • 应用场景：数据量较少，或者数据完全无序且只查一次的情况。

1.2 二分查找

  • 定义：也叫折半查找，在有序序列中，每次都拿中间的数来比对，排除掉一半的可能性。
  • 核心原理 ：分治法。
    • 比中间小？去左边找。
    • 比中间大？去右边找。
  • 时间复杂度 ： O ( l o g 2 n ) O(log_2n) O(log2n) （速度极快，找100万个数最多只需比对20次）。
  • 优点：查找效率非常高。
  • 缺点 ：前提必须是有序数组。如果为了查找而去专门做一次排序，成本可能划不来；不适合频繁插入删除的数据（维护有序性成本高）。
  • 应用场景：静态的、已排序的大量数据（如字典查字、图书馆索书号）。

1.3 哈希查找

  • 定义：通过一个数学公式（哈希函数），直接算出数据应该存放的地址。
  • 核心原理：地址映射。地址 = f(关键字)。
  • 时间复杂度 ：理想情况下为 O ( 1 ) O(1) O(1) （一次命中）。
  • 优点：查找速度最快，几乎不需要比较。
  • 缺点 ：需要额外的存储空间（空间换时间）；可能会产生"冲突"；数据是无序的。
  • 应用场景：需要极速查找的系统，如缓存系统（Redis）、数据库索引、身份证查询。

2. 排序

2.1 第一梯队（简单排序）

（1）直接插入排序
  • 核心原理 ：摸扑克牌。
    • 左手里手牌是有序的，右手摸一张新牌，插到左手牌中合适的位置。
  • 最好情况 ：数据本身就是有序的（只需要比较，不需要移动），效率极高 O ( n ) O(n) O(n)。
  • 稳定性：稳定。
  • 考点：当数据基本有序时，它是最快的排序方法。
（2）冒泡排序

📝 最基础的排序，不多说了

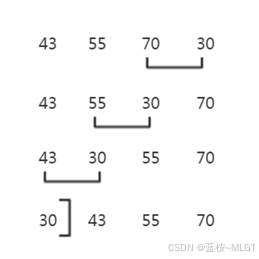
  • 核心原理 ：水中气泡上浮。
    两两比较，大的往后移。每一轮循环，最大的那个数就像气泡一样浮到了最后面。
  • 稳定性：稳定。
  • 考点：最基础，效率一般，但如果一轮比较下来没有发生交换，可以提前结束（优化点）。
（3）简单选择排序
  • 核心原理 ：挑苹果。
    • 第一次从一堆里挑出最小的，放在第一个位置；第二次从剩下的里面挑最小的，放第二个位置......
  • 稳定性 ：不稳定（⚠️重点）。
    • 例子：[5, 8, 5, 2]，第一轮会把第一个 5 和 2 交换，导致第一个 5 跑到了第二个 5 的后面，破坏了原有的顺序。
  • 考点 ：无论数据烂不烂，它都要比较 n ( n − 1 ) / 2 n(n−1)/2 n(n−1)/2 次，它是表现最稳定的"慢"（也就是最好最坏都是 O ( n 2 ) O(n^2) O(n2)

2.2 第二梯队（进阶排序）

（4）快速排序
  • 核心原理 ：分治法 + 基准兵。
    • 随便找个"基准数"（Pivot，比如第一个数）。
    • 把比它小的都扔左边，比它大的都扔右边。
    • 然后对左边和右边分别再做同样的事（递归）。
  • 优缺点 ：
    • 优点 ：平均速度最快。
    • 缺点 ：不稳定。最坏情况（数据本身倒序）会退化成冒泡排序 O ( n 2 ) O(n^2) O(n2)
  • 考点：它是所有同数量级排序中，平均性能最好的。但它对内存栈有消耗（递归）。
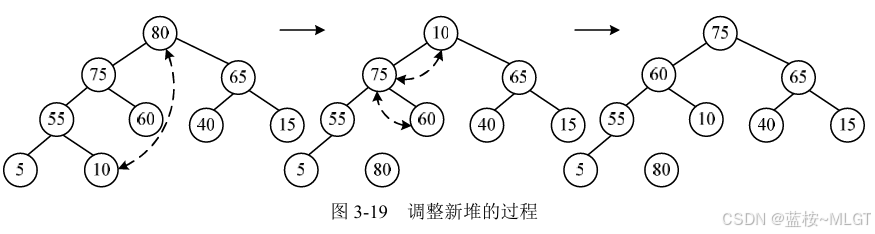
（5）堆排序
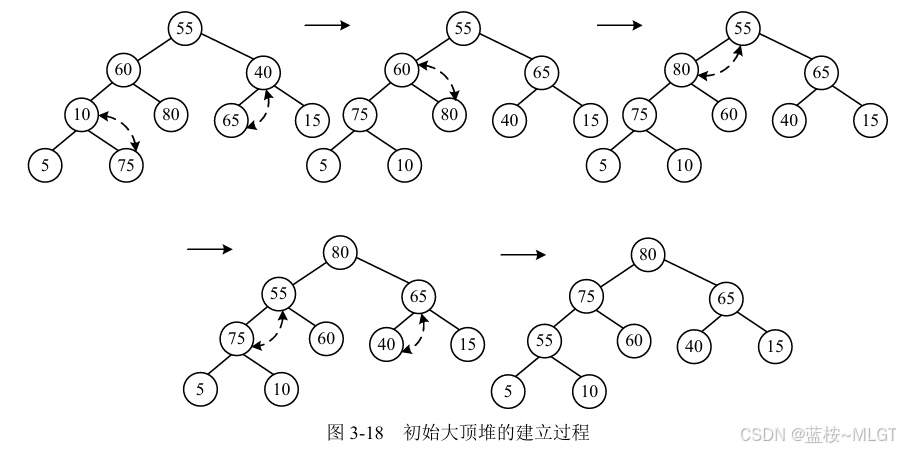
  • 核心原理 ：利用完全二叉树。
    • 把数据构建成一个大顶堆（根节点最大）。
    • 把堆顶（最大值）和末尾元素交换，排除末尾，剩下的重新建堆。
  • 优缺点 ：
    • 优点 ：空间复杂度 O ( 1 ) O(1) O(1)，不需要额外内存。
    • 缺点：不稳定。
  • 考点 ：适合求 "前 K 个最大/最小值" 的问题（Top K 问题）。
（6）归并排序
  • 核心原理 ：分而治之 + 合并。
    • 把数组从中砍断，一分为二，二分为四......直到切成单个元素。
    • 然后两两有序合并：[1,3] 和 [2,4] 合并成 [1,2,3,4]。
  • 优缺点 ：
    • 优点 ：稳定（这是它比快排和堆排强的点）。效率非常稳定，永远是 O ( n l o g n ) O(nlogn) O(nlogn)
    • 缺点 ：费空间。需要一个和原数组一样大的辅助空间 O ( n ) O(n) O(n)
  • 考点 ：空间换时间的典型代表。

2.3 特殊排序

（7）希尔排序
  • 核心原理 ：缩量增量 + 插入排序。
    • 它是插入排序的升级版。
    • 先按间隔 5 分组排序，再按间隔 3 分组排序，最后按间隔 1 排序。让数据宏观上先有序，最后微调。
  • 时间复杂度 ：突破了 O ( n 2 ) O(n^2) O(n2) 的界限，平均约 O ( n 1.3 ) O(n^{1.3}) O(n1.3)。
  • 稳定性：不稳定（因为跳着交换）。
  • 考点 ：它是第一个突破 O ( n 2 ) O(n^2) O(n2) 限制的排序算法。

2.4 总结

排序算法 平均时间 最坏时间 空间复杂度 稳定性 口诀/特征
冒泡 O(n²) O(n²) O(1) ✅ 稳定 两两交换，大数上浮
插入 O(n²) O(n²) O(1) ✅ 稳定 基本有序时最快
选择 O(n²) O(n²) O(1) ❌ 不稳定 最好最坏都很慢
希尔 O(n¹·³) O(n²) O(1) ❌ 不稳定 跳跃式插入
快排 O(n log n) O(n²) O(log n) ❌ 不稳定 平均性能最强
堆排 O(n log n) O(n log n) O(1) ❌ 不稳定 适合 TopK，省空间
归并 O(n log n) O(n log n) O(n) ✅ 稳定 费空间，效率稳

下一章：操作系统知识

相关推荐
代码游侠2 小时前
学习笔记——ESP8266 WiFi模块
服务器·c语言·开发语言·数据结构·算法
0和1的舞者2 小时前
Python 中四种核心数据结构的用途和嵌套逻辑
数据结构·python·学习·知识
乌萨奇也要立志学C++13 小时前
【洛谷】递归初阶 三道经典递归算法题（汉诺塔 / 占卜 DIY/FBI 树）详解
数据结构·c++·算法
鱼跃鹰飞14 小时前
Leetcode1891:割绳子
数据结构·算法
无限进步_16 小时前
【C语言&数据结构】对称二叉树：镜像世界的递归探索
c语言·开发语言·数据结构·c++·git·算法·visual studio
玖剹16 小时前
队列+宽搜（bfs）
数据结构·c++·算法·leetcode·宽度优先
C++ 老炮儿的技术栈18 小时前
什么是通信规约
开发语言·数据结构·c++·windows·算法·安全·链表
萧瑟其中～18 小时前
二分算法模版——基础二分查找，左边界查找与右边界查找（Leetcode的二分查找、在排序数组中查找元素的第一个位置和最后一个位置）
数据结构·算法·leetcode
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04Linux下V2Ray安装配置指南05Claude Code 2.1.2 升级报错？别折腾了，一行命令搞定06jdk21下载、安装（Windows、Linux、macOS）07【踩坑笔记】50系显卡适配的 PyTorch 安装08KGG转MP3工具|非KGM文件|解密音频092025-04-03 Latex学习1——本地配置Latex + VScode环境10Overleaf编译超时，超出免费计划编译时限（已解决）