**Hi，大家好，我是半亩花海。**在上节说明了迁移学习领域的基本方法（基于样本、特征、模型、关系的迁移）之后，本文主要将介绍迁移学习的第一类方法------数据分布自适应，重点阐述了边缘分布自适应的原理与应用。该方法通过缩小源域和目标域边缘概率分布的距离实现迁移，核心思想是利用特征映射使两域数据分布接近。文章详细讲解了迁移成分分析(TCA)方法，包括其基于最大均值差异(MMD)的距离度量、核矩阵变换以及优化目标，并通过可视化对比展示了TCA在数据分布对齐上的优势。该方法为处理不同分布数据提供了有效解决方案。
目录
数据分布自适应 (Distribution Adaptation) 是一类最常用的迁移学习方法。这种方法的基本思想是，由于源域和目标域的数据概率分布不同，那么最直接的方式就是通过一些变换，将不同的数据分布的距离拉近。 下图形象地表示了几种数据分布的情况。简单来说，数据的边缘分布不同，就是数据整体不相似。数据的条件分布不同，就是数据整体相似，但是具体到每个类里，都不太相似。
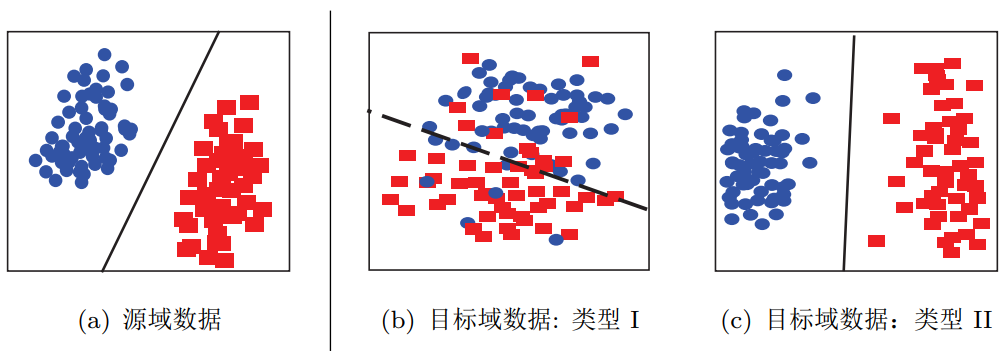不同数据分布的目标域数据
根据数据分布的性质，这类方法又可以分为边缘分布自适应、条件分布自适应、以及联合分布自适应。下面我们分别介绍每类方法的基本原理和代表性研究工作。介绍每类研究工作时，我们首先给出基本思路，然后介绍该类方法的核心，最后结合最近的相关工作介绍该类方法的扩展。
本文首先具体阐述边缘分布自适应的相关知识内容。
一、基本思路
边缘分布自适应方法 (Marginal Distribution Adaptation) 的目标是减小源域和目标域的边缘概率分布的距离，从而完成迁移学习。从形式上来说，边缘分布自适应方法是用 P(xs) 和 P(xt) 之间的距离来近似两个领域之间的差异。即：
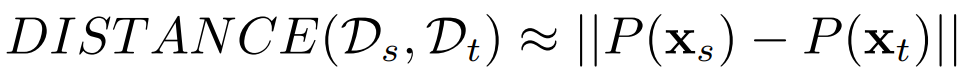
边缘分布自适应对应于上图中由图(a)迁移到图(b)的情形。
二、核心方法
边缘分布自适应的方法最早由香港科技大学杨强教授团队提出 Pan et al., 2011，方法名称为迁移成分分析 (TCA , Transfer Component Analysis)。由于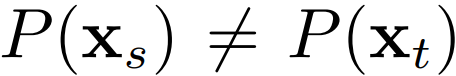 
，因此，直接减小二者之间的距离是不可行的。TCA 假设存在一个特征映射 
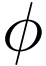，使得映射后数据的分布 
。TCA 假设若边缘分布接近，则两个领域的条件分布也会接近， 即条件分布 
。这就是 TCA 的全部思想。因此，我们现在的目标是，找到这个合适的 ϕ。
回到迁移学习的本质上来：最小化源域和目标域的距离。好了，我们能不能先假设这个 是已知的，然后去求距离，看看能推出什么呢？
更进一步，这个距离怎么算？机器学习中有很多种形式的距离，从欧氏距离到马氏距离，从曼哈顿距离到余弦相似度，我们需要什么距离呢？TCA 利用了一个经典的也算是比较"高端"的距离叫做最大均值差异 (MMD，maximum mean discrepancy)。我们令 n1, n2 分别表示源域和目标域的样本个数，那么它们之间的 MMD 距离可以计算为：
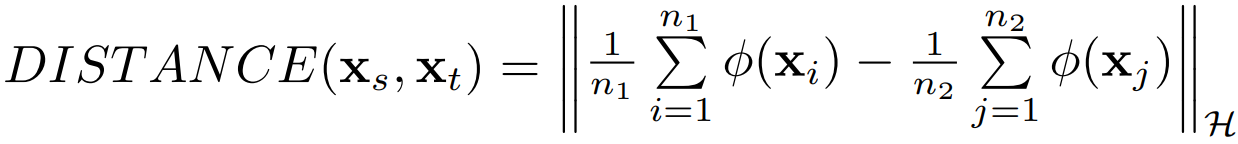
MMD 是做了一件什么事呢？简单，就是求映射后源域和目标域的均值之差。 事情到这里似乎也没什么进展：我们想求的 仍然没法求。 TCA 是怎么做的呢，这里就要感谢矩阵了！我们发现，上面这个 MMD 距离平方展开后，有二次项乘积的部分！那么，联系在 SVM 中学过的核函数，把一个难求的映射以核函数的形式来求，不就可以了？于是，TCA 引入了一个核矩阵 ：
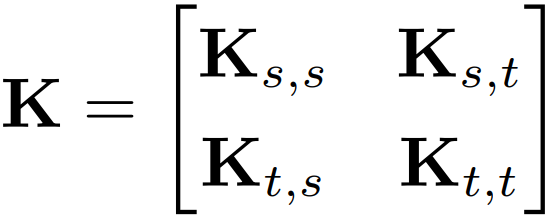
以及一个 MMD 矩阵 ，它的每个元素的计算方式为：
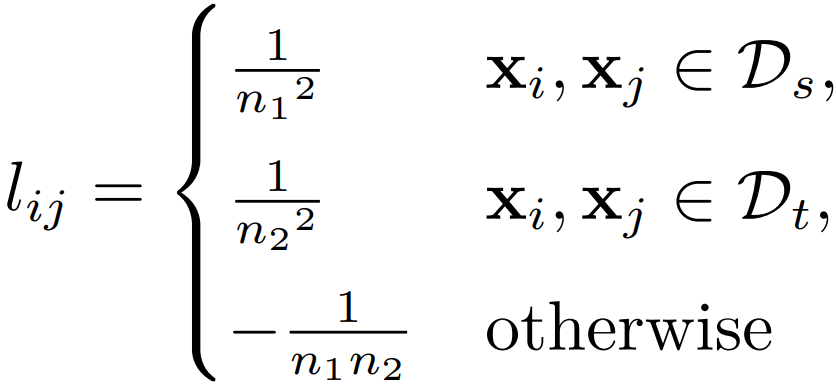
这样的好处是，直接把那个难求的距离，变换成了下面的形式：
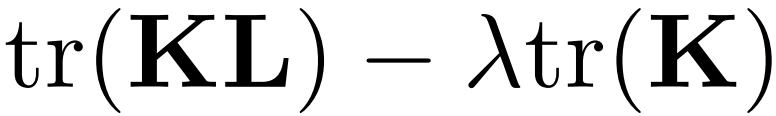
其中， 操作表示求矩阵的迹，用人话来说就是一个矩阵对角线元素的和。这样是不是感觉离目标又进了一步呢？
其实这个问题到这里就已经是可解的了，也就是说，属于计算机的部分已经做完了。只不过它是一个数学中的半定规划 (SDP，semi-definite programming) 的问题，解决起来非常耗费时间。由于 TCA 的第一作者 Sinno Jialin Pan 以前是中山大学的数学硕士，他想用更简单的方法来解决。他是怎么做的呢？
他想出了用降维的方法去构造结果。用一个更低维度的矩阵 ：
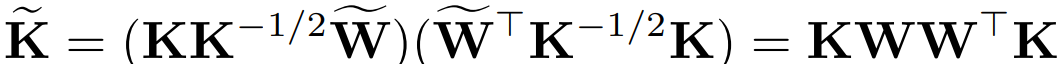
这里的 W 矩阵是比 K 更低维度的矩阵。最后的 W 就是问题的解答了！
好了，问题到这里，整理一下，TCA 最后的优化目标是：
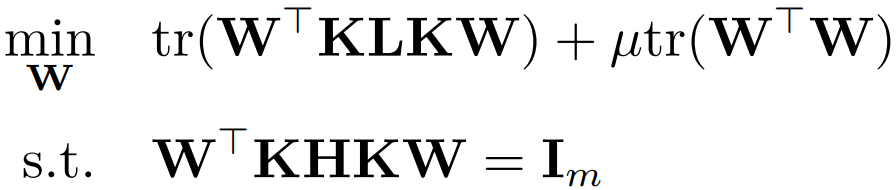
这里的 是一个中心矩阵，
。
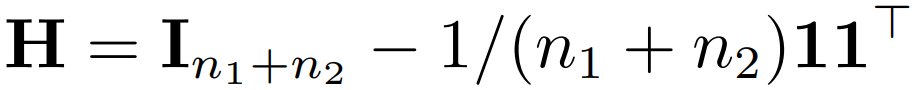这个式子下面的条件是什么意思呢？那个 min 的目标我们大概理解，就是要最小化源 域和目标域的距离，加上 W 的约束让它不能太复杂。那么下面的条件是什么呢？下面的条 件就是要实现第二个目标：维持各自的数据特征。
TCA 要维持的是什么特征呢？文章中说是 variance，但是实际是 scatter matrix，就是 数据的散度。就是说，一个矩阵散度怎么计算？对于一个矩阵 ，它的 scatter matrix 就是
。这个 就是上面的中心矩阵啦。
三、方法小结
好了，我们现在总结一下 TCA 方法的步骤。输入是两个特征矩阵，我们首先计算 和
矩阵，然后选择一些常用的核函数进行映射 (比如线性核、高斯核) 计算
，接着求
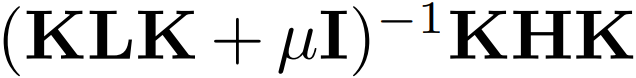的前 m 个特征值。仅此而已。然后，得到的就是源域和目标域的降维 后的数据，我们就可以在上面用传统机器学习方法了。
为了形象地展示 TCA 方法的优势，我们借用 Pan et al., 2011 中提供的可视化效果， 在图中展示了对于源域和目标域数据 (红色和蓝色)，分别由 PCA(主成分分析) 和 TCA 得到的分布结果。从图 20中可以很明显地看出，对于概率分布不同的两部分数据，在经过 TCA 处理后，概率分布更加接近。这说明了 TCA 在拉近数据分布距离上的优势。
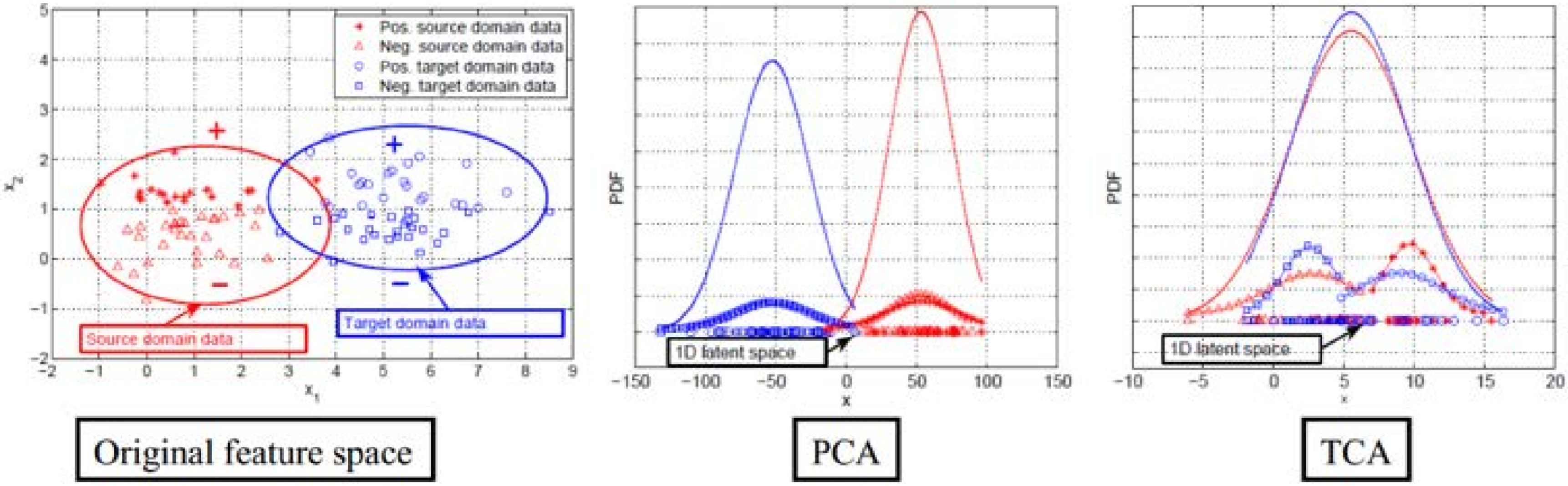TCA 和 PCA 的效果对比
四、参考资料
1. 王晋东《迁移学习简明手册》(PDF版) https://www.labxing.com/files/lab_publications/615-1533737180-LiEa0mQe.pdf#page=82&zoom=100,120,392
2. 《迁移学习简明手册》发布啦！ https://zhuanlan.zhihu.com/p/35352154