苏宁滑块VMP深入剖析(一)：解混淆篇

一直忙于工作，有段时间没更新了，最近发现个有意思的vmp样本，那就是苏宁滑块！在反爬圈，好像并没有阿里231京东h5st等一众反爬手段名气大，但实际苏宁滑块却不简单，别被他低调的外表所欺骗，个人认为，苏宁vmp的反爬思路比腾讯点选、百度旋转等一众vmp还要优秀。接下来我将尽可能的深入剖析一下这个vmp样本，由于担心单篇的篇幅太长，所以我会分成多篇来分析。废话少说，开始！

申明

本文章中所有内容仅供学习交流使用，不用于其他任何目的，严禁用于商业用途和非法用途，否则由此产生的一切后果均与作者无关！若有侵权，请添加（wx：ShawYbo）联系删除

目标网站

网站：

aHR0cHM6Ly9wYXNzcG9ydC5zdW5pbmcuY29tL2lkcy9sb2dpbg==

目标：解混淆

分析过程

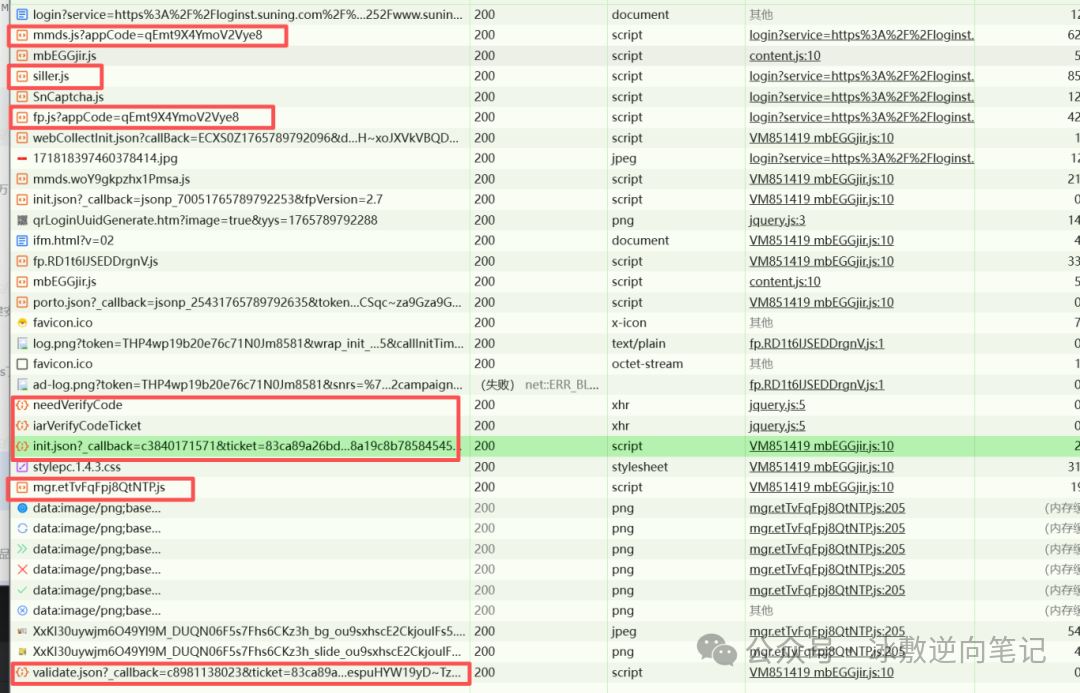
在上图中，我已经用红框标注出关键的请求的js文件了，接下来依序分析：

mmds.js：该js用于detect检测，用于后续的needVerifyCode请求中detect参数的构建，多次测试下来，发现needVerifyCode请求与整个验证流程无影响，所以这里不做过多分析。

**siller.js：**主要用于发送滑块验证的init请求，该js只做了解，无需处理。

**fp.js:**用于生成dfpToken，dfpToken会用于后续vmp流程中。

**needVerifyCode请求：**上面已经说了，对流程无影响，这个请求其实就是验证detect，并返回当前所登录账号是否需要弹出滑块验证。

**iarVerifyCodeTicket请求：**该请求用于申请ticket票据。

**init.json：**这是一个关键请求，响应内容包含了滑块混淆底图的正确还原顺序、图片下载oss地址和关键mgr.js动态地址等内容。

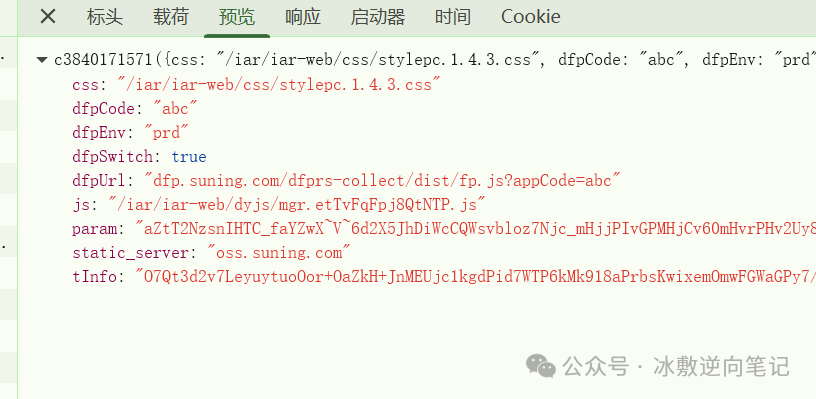
mgr.xxxx.js：这是这次样本的关键js，负责解析init.json加密响应和构建滑块验证请求参数。从js名字可以看出这是动态加密，一个ticket对应一个mgr.js，意味着不同mgr.js的代码和加密流程不同（这一点如同谷歌的recaptcha）。

**validate.json：**这个就是验证请求了，如果校验通过，会返回一个token。

混淆还原

对于vmp来讲，一般不需要特别在意混淆，因为所有逻辑是在虚拟机中通过指令操作完成，而不是暴露在代码中，只要能debug就行，所以还原混淆对于vmp来讲可有可无。但是这个样本的混淆方式不多见，所以这里还是还原一下。

该样本主要用的混淆方式为函数柯里化 、链式赋值 和逗号表达式。逗号表达式比较常见，这里不赘述，接下来分析一下函数柯里化和链式赋值。

什么是函数柯里化？函数柯里化是指将一个多参数函数转化为一系列单参数函数的调用链。

普通函数：

javascript 复制代码

function add(a, b, c) {
    return a + b + c;
}
add(1, 2, 3); // 6
    柯里化后：

function add(a) {
    return function(b) {
        return function(c) {
            return a + b + c;
        }
    }
}
add(1)(2)(3); // 6

mgr.js中运用了大量的三层柯里化函数，这类函数的变量大多藏在闭包中，debug时难以追踪，且函数并不会立即执行，动态分析时难以找到所有参数。但是对于柯里化，我们不做处理。后面说明原因。

另一个显著混淆特征就是链式赋值了，通过大量变量声明和赋值操作压缩到一个表达式中，最终形成一个难以阅读且难以debug的代码块。

混淆前代码：

javascript 复制代码

n = function () {};
h = function (s) { /* ... */ };
t = function (i) { /* ... */ };
j = function (n) { return +n; };

混淆后：

javascript 复制代码

x = ((h = (n = function () {
}, function (s) {
    return s = w(s), function (n, e, t, j, i, l, r, y, o) {
        if (!rn(U(n))) {
            if ((i = (j = q(en(n)), In)(j), (l = 2, -1) < i(g)) && (l = 3), $(U(n))) e = [n];
        }
        return t
    }
}), l = (i = (y = (j = (t = function (i) {
    return function (j) {
        return function (e, n, t) {
            return (t = (n = e.o(0), i) ? 0 : M(x(e.l, 1), function (n) {
                return e.n(n)
            }), n) && j(n, t)
        }
    }
}, function (n) {
    return +n
}), function (n, e, t) {
    return (((t = z(), t).U = {M: e, n: []}, t[(t.U.d = n.U, "U")]).U = z(), t)[(t.l = n.l, "M")] = n.M, t
}), function (n, e) {
    return n + e
}), Object)), function (n, e, t) {
    return t === undefined ? n.slice(e) : n.slice(e, t)
});

该种混淆的特点：

多达10层以上的嵌套赋值。
每个赋值操作的右侧又可能是另一个链式赋值。
代码横向展开极长，变量定义难以追踪。

我们可以使用AST来把链式赋值展开：

javascript 复制代码

AssignmentExpression(path) {
    const {left, right} = path.node;
    // 避免在 SequenceExpression 内部重复处理
    if (path.parent.type === 'SequenceExpression') return;
    const statements = [];
    // 处理左侧的 SequenceExpression
    let newLeft = left;
    if (containsSequenceExpression(left)) {
        const leftResult = extractSequenceFromExpression(left);
        statements.push(...leftResult.statements);
        newLeft = leftResult.remaining;
    }
    // 处理右侧的 SequenceExpression
    let newRight = right;
    if (containsSequenceExpression(right)) {
        const rightResult = extractSequenceFromExpression(right);
        statements.push(...rightResult.statements);
        newRight = rightResult.remaining;
    }
    // 添加最终的赋值
    statements.push(
        t.expressionStatement(
            t.assignmentExpression('=', newLeft, newRight)
        )
    );
    // 替换节点
    if (t.isExpressionStatement(path.parent)) {
        path.parentPath.replaceWithMultiple(statements);
        path.skip();
    }
}

转换示例：

javascript 复制代码

// 混淆前
x = (a = 1, b = 2, c = 3, a + b + c);
// 还原后
a = 1;
b = 2;
c = 3;
x = a + b + c;

思路就是是将逗号表达式（SequenceExpression）拆解为独立语句。

逗号表达式 (a, b, c) 会依次执行a、b、c，但只返回最后一个值c。转化时将前面的表达式提取为独立语句，保留最后一个作为返回值。

三步流程：

识别 - 通过AST检测 SequenceExpression 节点
提取 - 递归提取前N-1个表达式转为语句，保留最后一个
替换 - 用新的语句序列替换原节点

处理嵌套：遇到 var x = ((y = (z = 1, 2), 3)) 这种嵌套结构，从最内层开始递归展开，最终得到 z=1; y=2; var x=3;

语 义保护：短路求值（&&、||）和条件表达式的分支不展开，避免改变执行逻辑。

javascript 复制代码

// 嵌套的复杂情况
var x = ((h = (n = fn1, fn2), l = obj), slice);
// 递归处理：
// 第1层内层: n = fn1
// 第2层中层: h = fn2
// 第3层外层: l = obj
// 第4层最外: x = slice
// 结果
n = fn1;
h = fn2;
l = obj;
x = slice;

PS：AST还原的基本原则是语义等价，也就是说还原后的代码一定要和还原前的代码执行结果相等，尤其是||和&&具有短路性质，这一点要注意。

你可能会问：既然我们展开了链式赋值和逗号表达式，为什么不把柯里化也展开呢？原因有以下几点：

链式赋值和逗号表达式是语法糖 ，可以展开为等价的语句序列，而柯里化是函数的本质特性，展开会改变函数的行为和接口，所有调用该函数的地方都需要修改。
另外，当前样本是vmp，柯里化对于流程的影响并不是那么重要，因为所有细节都在指令中，只是一些加减乘除等基础运算操作函数被柯里化，但这不影响我们分析。

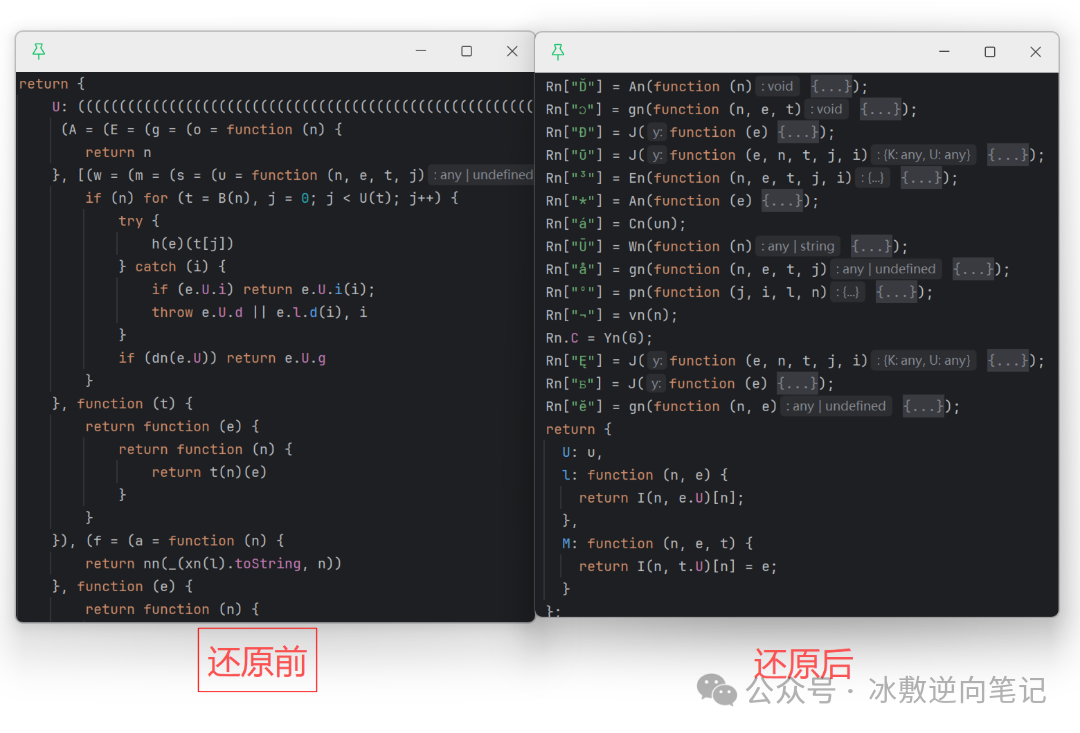
链式赋值还原完后，就可以插桩分析vmp补环境和纯算了。下一篇继续分析，通过补环境模拟滑块滑动过程。

可添加宫中号：冰敷逆向笔记

一起交流学习。。。