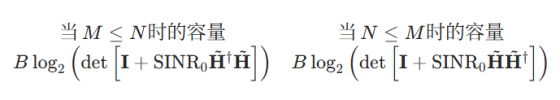MIMO 信道
多输入多输出(MIMO)信号传输的概念已不止于单纯的天线分集。在 MIMO 无线链路中,一个数据流会被拆分为多个独立信号,通过空间中可区分的多径信道发送。
尽管多天线集成、信号处理等实际考量让 MIMO 信号传输成为一项严峻的技术挑战,但许多工程师仍将这类技术视为带宽受限无线通信的未来。事实上,通过巧妙利用空间维度,海量数据有望被压缩到极小的信号频谱中。
用 "多天线 + 空间维度" 提升无线通信的 "数据传输能力"(容量)
不增加带宽,只靠多天线和信号处理,让数据传输速度 "成倍提升"
MIMO 的关键不是 "多加几个天线",而是让多个天线协同工作,把 "空间" 变成一个新的 "数据通道",不用额外占用带宽,就能多传数据
传统多天线系统
多天线系统的香农极限性能------ 这类系统旨在最大化无线信道中的信号功率。
在深入学习空时分组码与 MIMO 架构前,必须先理解这些基础场景。
举个具体例子:
- SISO:1 车道公路,一次只能过 1 辆车;
- SIMO/MISO:1 车道,但路面变宽(减少拥堵 / 噪声),车能开得更稳(信号更好),但还是 1 辆车;
- MIMO:直接变成 "min (M,N) 条车道"(比如 2 发 3 收 = 2 条车道),一次能过 2 辆车,速度直接翻倍。
单输入单输出(SISO)
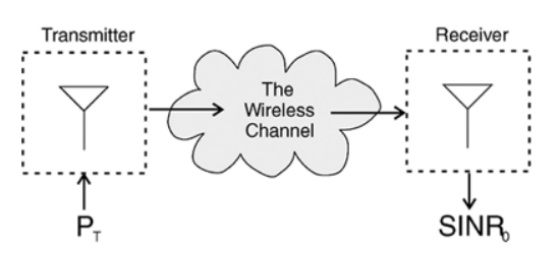
对于给定信道与发射端输入功率PT,接收端会得到平均信干噪比为SINR0的信号。据此,我们至少可以估计出信道容量的香农极限为:
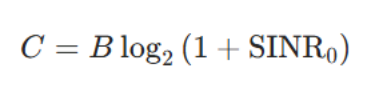
发射端单天线→无线信道→接收端单天线
其中B是可用带宽。显然,SINR0是影响信道容量的关键参数。
单输入多输出(SIMO)
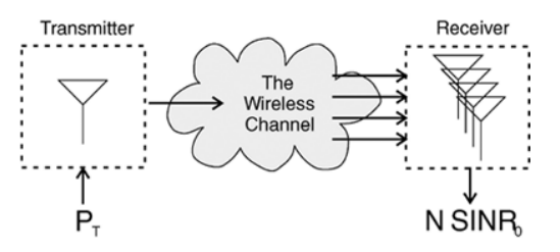
接收端采用N个天线,会得到N个衰落信号的副本。若这些信号的平均幅度相同,可通过相干叠加使信号功率提升(N^2)倍。当然,同时也会叠加N组噪声 / 干扰,但幸运的是,噪声与干扰是非相干叠加,仅使噪声功率提升N倍。因此,信干噪比仍会获得净提升:

发射端单天线→无线信道→接收端N个天线
据此逻辑,该系统的信道容量近似为:
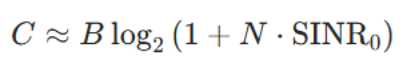
这比 SISO 场景的容量更高。
多输入单输出(MISO)
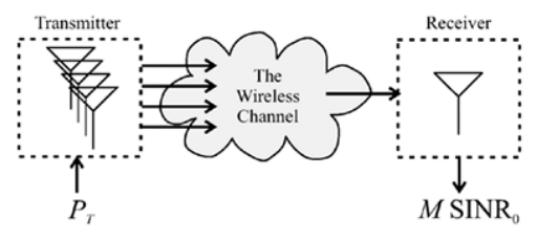
发射端采用M个天线,因此总发射功率会分配到M个发射分支中。尽管每个发射天线的功率会降低,但发射端天线可通过相位调整,使信号在接收端实现相干叠加;实际接收信号的 SINR 会比 SISO 场景净提升约M倍。由于仅存在一个接收信道,接收噪声 / 干扰功率保持不变,最终 SINR 的提升为:

发射端M个天线→无线信道→接收端单天线
据此逻辑,该系统的信道容量为:
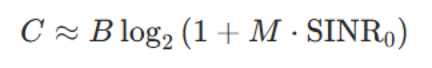
多输入多输出(MIMO)
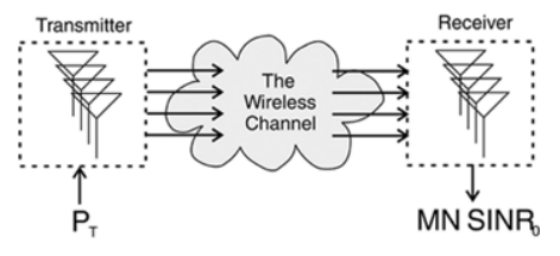
发射端有M个天线,接收端有N个天线。我们可将其视为 SIMO 与 MISO 场景的结合:通过调整各天线的相位,使信号在无线信道中实现总信号功率最大化的收发,最终接收信号的 SINR 会(近似)提升MN倍。
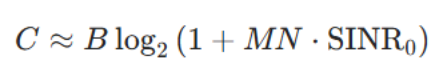
这一容量远大于单独 SIMO 或 MISO 场景的容量。
发射端M个天线→无线信道→接收端N个天线
在多径中分离信道
MIMO 信道矩阵
需要建立 MIMO 系统的矩阵信道模型
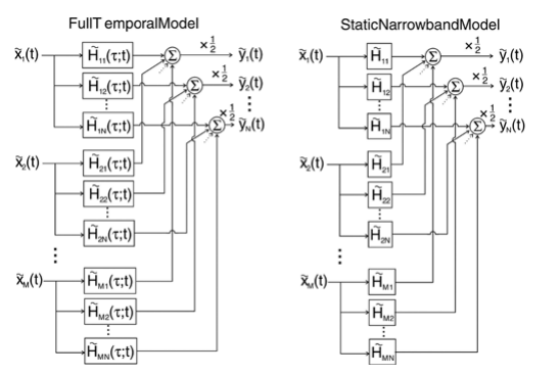
图中是通用的 MIMO 信道模型,
该模型描述了 "输入到 M 个发射天线的信号集
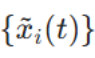
" 与 "N 个接收天线处接收到的信号集
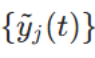
"之间的各个传递函数
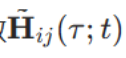
。此外,这些信道可以是时间t的函数(用于建模时变信道),也可以是时延(\tau)的函数(用于建模宽带传输带来的色散)。
左侧为 "全时域模型",右侧为 "静态窄带模型",展示了发射信号经传递函数到接收信号的过程
在这种复杂系统中,用向量 / 矩阵表示法来记录所有收发信号是一种实用的记录方法。
接收信号向量(即 N 个接收天线的输入信号)可由发射信号向量计算得到;输出向量与输入向量通过信道传递矩阵关联,关系如下:
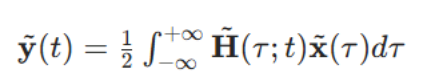
其中:
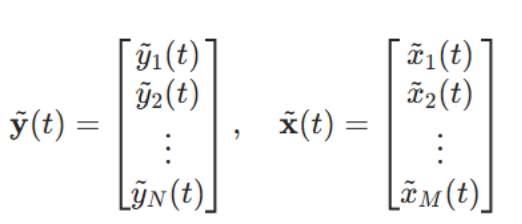
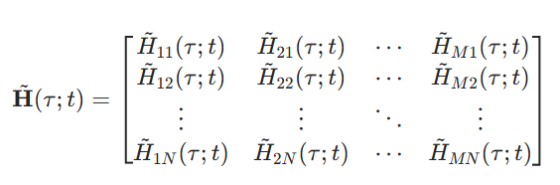
在该表示中,
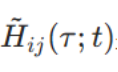
是第i个发射天线到第j个接收天线的信道冲激响应(CIR)。为了简化理解,通常采用窄带、时不变的信道模型(不损失一般性):此时信道无频率或时间依赖性,信道矩阵H为常数矩阵:
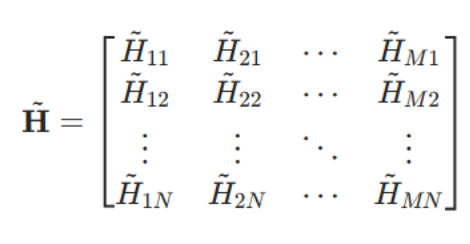
这会将接收信号集的计算简化为:
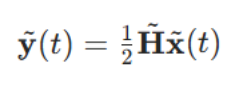
该公式是 MIMO 容量分析的基础。
MIMO 信号处理
MIMO 系统可通过收发端的信号处理,得到整体容量最高的接收信号集。对收发信号向量的处理采用线性重组(以矩阵乘法表示)
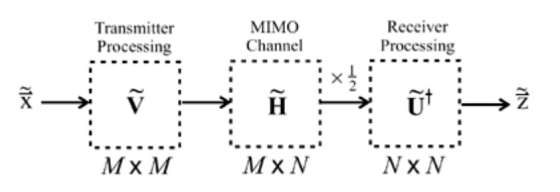
MIMO 系统中信号处理操作的矩阵表示

发射端处理
信号向量的模长代表总信号功率。我们对发射信号向量执行线性处理操作,得到输入发射天线阵列的新信号集

酉矩阵不会改变向量的几何长度,因此不会增加总发射信号的功率(这一点很重要,因为我们要体现仅由 MIMO 信号处理带来的容量增益,而非发射端放大的效果)。
符号†代表共轭转置(即 Hermitian 操作)
例如:
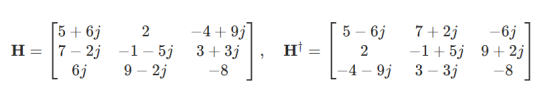
通常,基带 MIMO 信道矩阵不是Hermitian 矩阵。
接收端处理
接收端也可执行信号处理:信道对发射端输出信号作用后得到
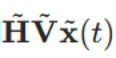
接收端用矩阵对输入信号进行处理,最终输出信号向量
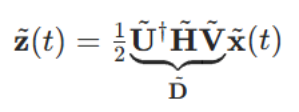

这一条件确保不会增减信号功率 ------ 接收端只是通过简单的线性组合操作重排了输入信号
当然,无线系统难以控制信道矩阵,但可以控制U和V矩阵,我们可在 MIMO 链路中采用算法,将整体操作对角化

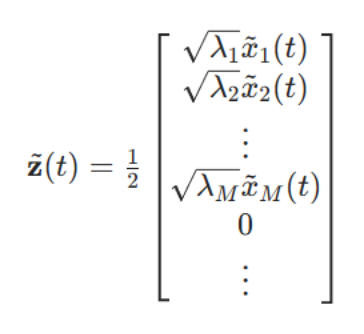
从数学角度看,当(M \leq N)时,MIMO 信道可被视为一组从发射端到接收端的M个独立信道。
若发射天线数多于接收天线数((M > N)),对角矩阵最多支持N个独立信道。因此,具有M个发射天线和N个接收天线的无线链路中,独立信道的数量为(\min(M,N))
奇异值分解
SVD 的作用是 "拆分混合信道,变出独立通道",独立通道的数量 = 发射天线数和接收天线数里的 "小数"
前文的信号处理步骤有明确的物理依据:它们在不增减功率(也不通过放大改变信道容量)的前提下重排了信号。而我们实际执行的操作,是对信道矩阵H进行奇异值分解(SVD)。我们可将公式重排为:
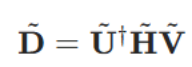
得到:
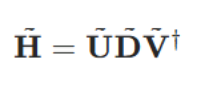
这正是矩阵的奇异值分解(SVD)定义。此外,SVD 定理指出:D的非零对角元素(即H的奇异值)具有特殊且重要的数学意义 ------ 将其平方后,实际是矩阵

(当(N≥M)时)或矩阵
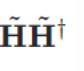
(当(M ≥N)时)的特征值。
分离信道
若每个信道传输的是相同信号,我们可以对z(t)中的信号分支进行相干合并,得到与公式 9.1.6 相近的容量。但如果x(t)中的每个信号都是不同信号,那么z(t)对应的各独立信道的容量大致为:N≥M
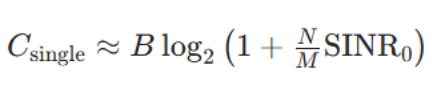
而这样的信道共有M个,因此系统的总容量为:
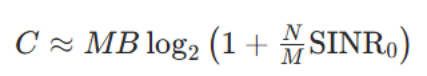
注意公式 9.2.11 与传统多天线信道容量公式 9.1.6 的区别:每个信道的 SINR 会降低,但由于存在M个信道,整体容量会倍增。
正式容量表达式
为推导带宽为B的平坦衰落 MIMO 信道的传统香农容量公式,我们从公式 9.2.5 的基本传输方程出发,为接收信号加入噪声与干扰:

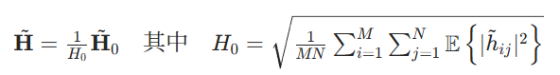
利用归一化信道矩阵,我们可以通过对每个独立信道的香农容量求和,得到总理论信道容量:
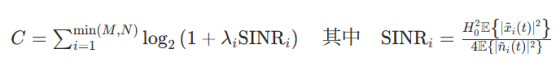

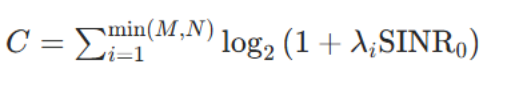
该公式假设发射端为每个独立信道分配了相等的功率。
"注水策略":相当于给 "信号质量好的独立通道" 多分配点 "功率"(比如让 A 说得更清楚),给 "信号差的通道" 少分配点,这样能进一步提升速度 ------ 但实际中很少用,因为需要接收端告诉发射端 "哪个通道好"(信道反馈),太麻烦,所以大多时候还是 "平均分配功率"。
实际上,通过根据注水策略为各独立信道分配不等的功率,可以提升公式 9.2.16 的容量。注水策略会按比例向更强的信道分配更多功率:例如,若信道 1 的强度是信道 2 的 2 倍,则信道 1 的功率分配也会是信道 2 的 2 倍。此时系统的总信道容量为:
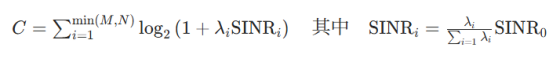
当然,发射端要实现注水策略的功率分配,必须知晓信道的 SVD。由于在无线通信系统中,从接收端向发射端反馈信道信息并不理想,因此公式 9.2.16 是大多数 MIMO 分析中的实际性能上限。
我们也可以不用奇异值来表示容量,而是基于归一化信道矩阵推导出更简洁的信道容量公式。MIMO 系统的标准容量公式通常表示为: