感知机是由美国学者Frank Rosenblatt在1957年提出来的。它是作为神经网络(深度学习)的起源的算法。因此, 学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。

本文章知识来源于《深度学习入门》 (鱼书),特此声明。可以当做读数笔记来进行阅读。
1.感知机是什么
如图,是个感知机,可以接收多个输入信号,输出一个信号。
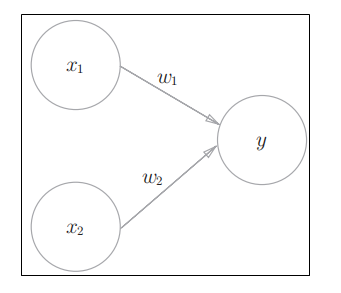
x1,x2 是输入信号,y是输出信号。 w1和w2 是权重。 输入信号被送往神经元时,会被分别乘以固定的权重(x1w1, x2 w2) . 神经元计算传送过来的信号的总和,只有当这个总和超过了某个界限值的时候,才会输出1. 这个界限值叫做 阈值, 用符号 θ 表示:
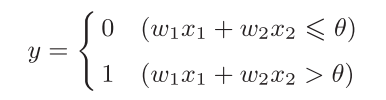
为什么要将输入和权重做乘积后求和,即加权求和?
神经网络的目标是学习输入与输出之间的映射关系。对于一个神经元来说,每个输入特征对最终输出的贡献是不同的。权重(weight)就代表了每个输入特征的"重要性"或"影响力"。
这是一个线性组合(linear combination),用来衡量输入特征在当前任务下的"加权活跃度"。
人工神经元是受生物神经元启发的. 生物神经元接收来自其他神经元的信号(通过突触),每个突触的"强度"不同(相当于权重)。如果所有输入信号的加权总和超过某个阈值,神经元就会"激活"(发放脉冲)。
2.用感知机解决逻辑电路
- 与门真值表
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
现在要做的就是:设定什么样的 w1,w2, θ , 经过计算后,能满足上面的真值表呢?
| x1 | w1 | x2 | w2 | θ | y |
|---|---|---|---|---|---|
| 0 | 0.5 | 0 | 0.5 | 0.7 | (满足0<=0.7) 0 |
| 1 | 0.5 | 0 | 0.5 | 0.7 | (满足0.5<=0.7) 0 |
| 0 | 0.5 | 1 | 0.5 | 0.7 | (满足0.5<=0.7) 0 |
| 1 | 0.5 | 1 | 0.5 | 0.7 | (满足1> 0.7) 1 |
这说明 (w1,w2,θ) =(0.5,0.5,0.7) 的时候可以满足真值表。
但是 (w1,w2,θ) =(0.5,0.5,0.8) 的时候同样可以满足真值表。
而且 (w1,w2,θ) =(1.0,1.0,1.0) 也可以满足。设定这样的参数后,仅当 x1和 x2同时为1时,信号的加权总和才会炒作给定的阈值 θ
- 与非门
我们 用(w_1 , w_2_, θ_) = (−_0 .5 , −0.5, −0._7)这样的组合试一试:
| x1 | w1 | x2 | w2 | θ | y |
|---|---|---|---|---|---|
| 0 | -0.5 | 0 | -0.5 | -0.7 | (满足0> -0.7) 1 |
| 1 | -0.5 | 0 | -0.5 | -0.7 | (满足 -0.5> - 0.7) 1 |
| 0 | -0.5 | 1 | -0.5 | -0.7 | (满足- 0.5> - 0.7) 1 |
| 1 | -0.5 | 1 | -0.5 | -0.7 | (满足 -1<= -0.7) 0 |
- 或门
我们 用(w_1 , w_2_, θ_) = (_1, 1, 0._7)这样的组合试一试:
| x1 | w1 | x2 | w2 | θ | y |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0.7 | (满足0<=0.7) 0 |
| 1 | 1 | 0 | 1 | 0.7 | (满足1> 0.7) 1 |
| 0 | 1 | 1 | 1 | 0.7 | (满足1>0.7) 1 |
| 1 | 1 | 1 | 1 | 0.7 | (满足2> 0.7) 1 |
与门、与非门、或门的感知机构造是一样的。 实际上,3个门电路只有参数的值(权重和阈值)不同。也就是说,相同构造 的感知机,只需通过适当地调整参数的值,就可以像"变色龙演员"表演不 同的角色一样,变身为与门、与非门、或门。
下面用python代码来实现:
python
def AND(x2,x2) :
w1,w2,theta = 0.5 ,0.5 ,0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1在函数内初始化参数w1、w2、theta,当输入的加权总和超过阈值时返回1, 否则返回0:
AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1
3.权重和偏置
我们将其变换为另外一种实现形式:
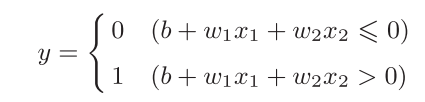
此处,_b_称为偏置,_w_1和_w_2称为权重。 只不过是把 θ 换成了b而已,本质没有发生变化
python
x = np.array([0, 1]) # 输入
w = np.array([0.5, 0.5]) # 权重
b = -0.7 # 偏置
w*x # array([ 0. , 0.5])
np.sum(w*x) # 0.5
np.sum(w*x) + b # -0.19999999999999996按照这个思路,修改上面的 AND:
python
def AND(x2,x2) :
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b= -0.7
tmp=np.sum(w*x)+b
if tmp <= theta:
return 0
elif tmp > theta:
return 1_w_1和_w_2是控制输入信号的重要性的参数,而偏置是调整神经元被激活的容易程度(输出信号为1的程度)的参数。比如,若_b_为 −_0 .1,则只要输入信号的加权总和超过0._1,神经元就会被激活。但是如果_b _
为_−20.0,则输入信号的加权总和必须超过20 .0,神经元才会被激活。像这样, 偏置的值决定了神经元被激活的容易程度。另外,这里我们将_w_1和_w_2称为权重, 将_b_称为偏置,但是根据上下文,有时也会将_b、_w_1、_w_2这些参数统称为权重。
4.线性和非线性
前面将真值表中的数据,带入函数中,预期的刚刚好就是准确的结果,上面的函数本就是一个线性函数。如果将它绘制在平面坐标系内,如果所有的输入,输出的点都在直线上,那么这个就能100% 预测。但是现实中很难找到一个准确的 (b,w1,w2) ,能让结果都分布在直线上。那就需要用非线性的空间了。
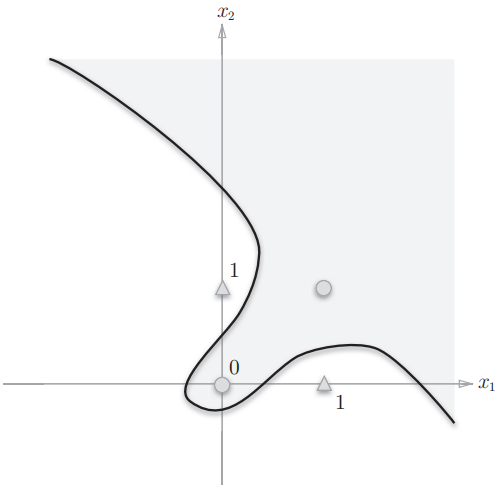
即函数不再是一个直线了。
5.多层感知机
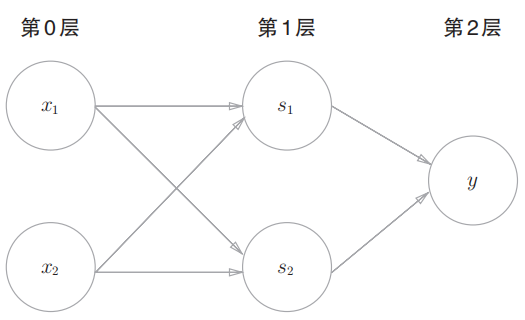
感知机总共由 3层构成,但是因为拥有权重的层实质 上只有 2层(第 0层和第 1层之间,第 1层和第 2层之间),所以称 为"2层感知机"。不过,有的文献认为图 2-13的感知机是由 3层 构成的,因而将其称为"3层感知机"。
多层感知机可以实现比之前见到的电路更复杂的电路。比如,进行加法 运算的加法器也可以用感知机实现。此外,将二进制转换为十进制的编码器、 满足某些条件就输出1的电路(用于等价检验的电路)等也可以用感知机表示。 实际上,使用感知机甚至可以表示计算机!
设定权重的工作,即确定合适的,能符合预期的输入输出的权重,是需要人工进行的。前面我们使用了真值表人工决定了合适的权重。
神经网络的一 个重要性质是它可以自动地从数据中学习到合适的权重参数.