线性回归实战下与深度学习概念

深度学习

目录

1.线性回归实战(下)

2.深度学习的概念

文章概述

深度学习（Deep Learning）是机器学习（Machine Learning）中的一个子领域，它通过模拟人脑的神经网络来处理和分析数据。深度学习的核心是神经网络

一、线性回归实战(下)

我们这边完成一下上一篇文章没有完成的内容。

我们直接可以拿上一篇文章里面, 已经处理好的train.csv拿来实验即可。

我们这边就直接展示房价预测的那部分代码。

首先, 我们得先设置固定随机性, 为什么要设置固定随机性的问题已经在上一篇文章中已经讲到过了, 那这边就不再细讲了(可以去翻上一篇文章的内容)。直接上代码：

import numpy as np
import torch


def seed_everything(seed=42):
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False


seed_everything()

我们导入上一篇文章已经处理好的train.csv文件:

import pandas as pd

train_data = pd.read_csv('train.csv')
train_data

结果:

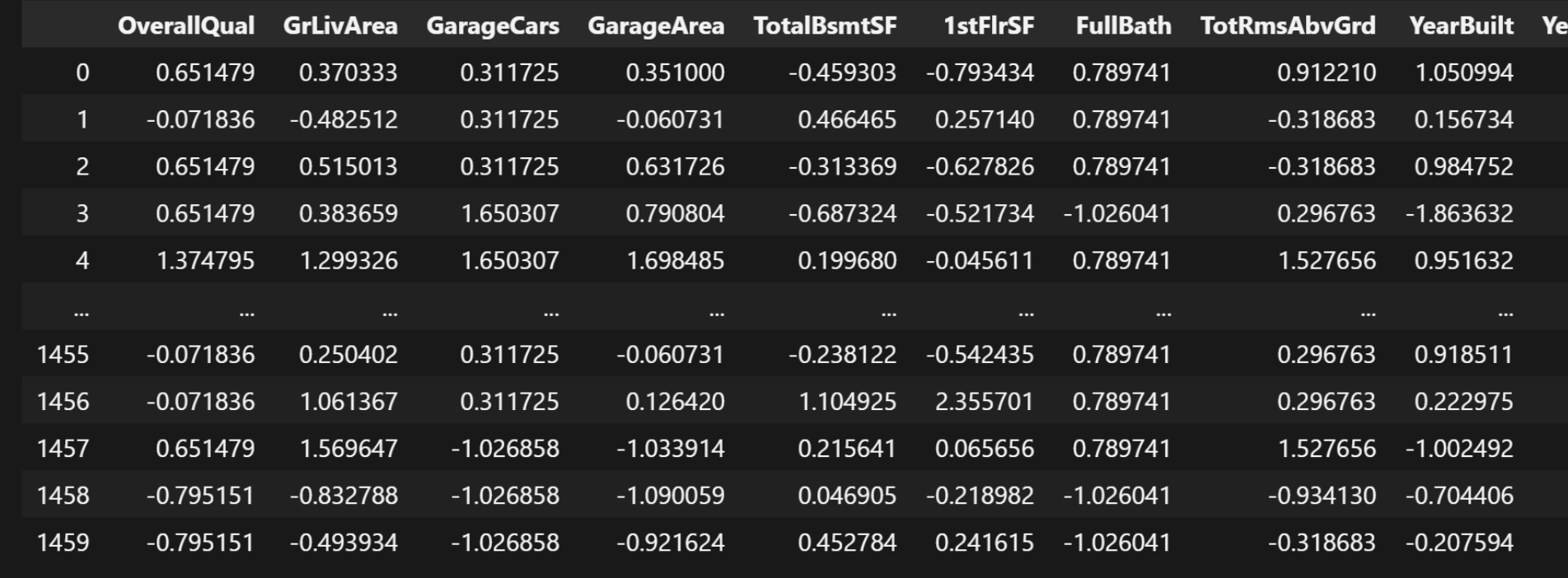
我们需要获取到特征和标签:

# 特征和标签
X_strandard_data = train_data.drop('SalePrice',
                                   axis=1)  # 对dataframe做删除-dataframe
Y_strandard_data = train_data['SalePrice']  # 去dataframe的一列-series
X_strandard_data

特征就是除了房价数据, 其它所有列都作为特征, 只有房价这一类作为标签, 因为我们是需要预测房价, 所以标签只能是房价。

运行结果:

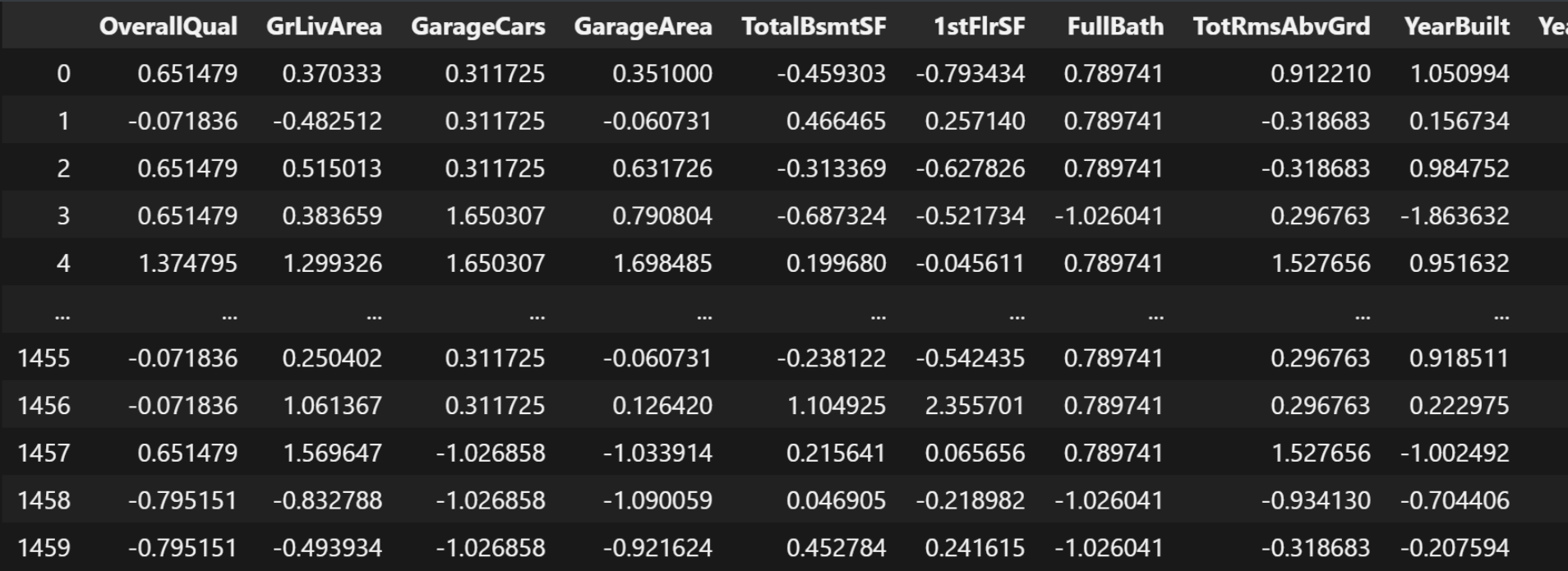
这里是特征数据集的结果。

我们可以查看下标签数据的结果:

Y_strandard_data

运行结果:

0       208500
1       181500
2       223500
3       140000
4       250000
         ...  
1455    175000
1456    210000
1457    266500
1458    142125
1459    147500
Name: SalePrice, Length: 1460, dtype: int64

随后我们需要对标签数据也标准化:

from sklearn.preprocessing import StandardScaler

Y_trandard = StandardScaler()
Y_standard_data = pd.DataFrame(Y_trandard.fit_transform(
    Y_strandard_data.to_frame()),
                               columns=['SalePrice'])
Y_standard_data

特征数据在上一篇文章里面已经做标准化了, 这里就不再演示了。

接下来, 我们就要划分数据集了:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_strandard_data,
                                                    Y_standard_data,
                                                    test_size=0.3)
X_train

我们将训练集划分70%, 验证集划分30%。

运行结果:

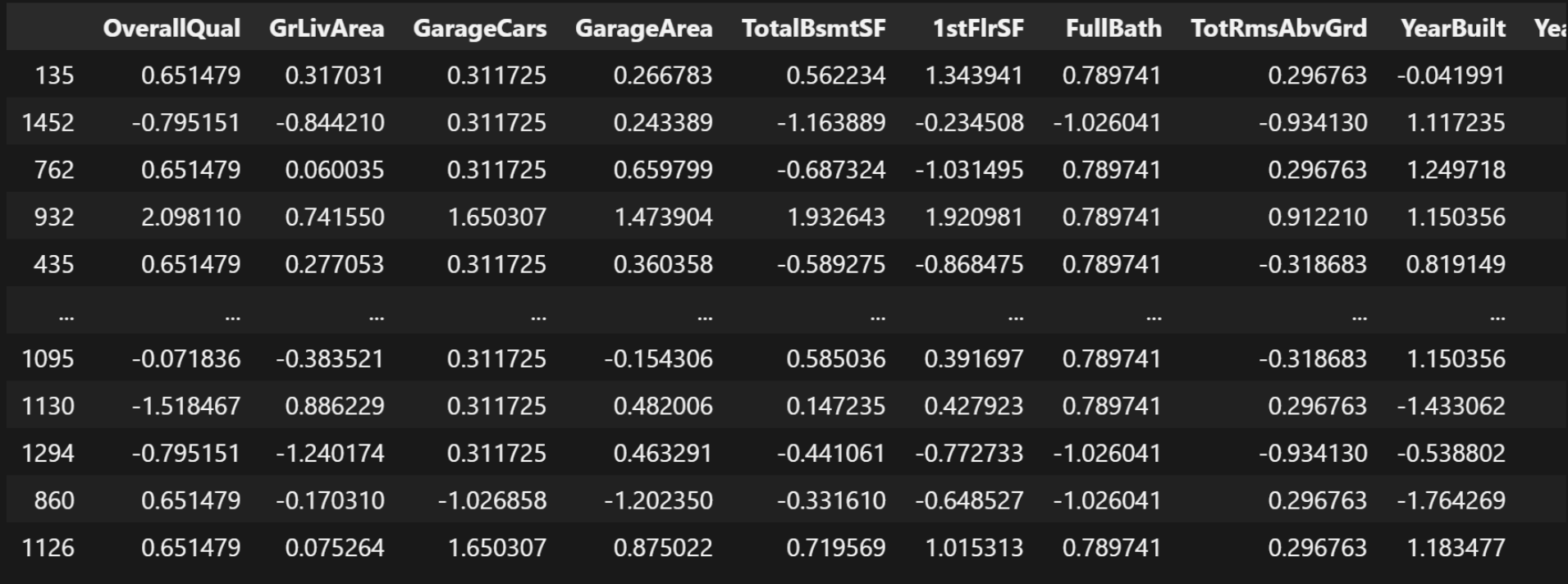
我们训练模型, 需要用GPU来跑, 如果自己电脑没有GPU, 那用CPU也行。

import torch

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device

运行结果:

device(type='cuda')

我们将所有的训练集和验证集都放入都device里面, 这样我们所有的数据都可以在GPU上跑了。

X_train_tensor = torch.tensor(X_train.values, dtype=torch.float32).to(device)
y_train_tensor = torch.tensor(y_train.values, dtype=torch.float32).to(device)
X_test_tensor = torch.tensor(X_test.values, dtype=torch.float32).to(device)
y_test_tensor = torch.tensor(y_test.values, dtype=torch.float32).to(device)
X_train_tensor.shape

运行结果:

torch.Size([1022, 10])

我们可以看到X训练集有1022个特征, 10个标签

接下来, 我们可以用数据加载器, 来批量进行数据划分(64个样本为一组)。

from torch.utils.data import TensorDataset, DataLoader

train_dataset = TensorDataset(X_train_tensor, y_train_tensor)  # [特征-标签]
train_loader = DataLoader(
    train_dataset, batch_size=64,
    shuffle=True)  # DataLoader 数据加载器 批量划分 batch_size=64 64个样本为一组
len(train_loader)

我们可以提取一组示例来验证:

# 提取一个示例来检查验证
examples = enumerate(train_loader)  # [(0,[特征,标签]),()]
batch_idx, (example_data, example_targets) = next(examples)
batch_idx, example_data.shape, example_targets.shape

结果:

(0, torch.Size([64, 10]), torch.Size([64, 1]))

我们分别输出example_data和example_targets:

example_data[0], example_targets[0]

结果:

(tensor([ 0.6515, -0.1665,  0.3117,  0.3791,  0.8199,  0.6867,  0.7897, -0.3187,
          1.2166,  1.1209], device='cuda:0'),
 tensor([0.5888], device='cuda:0'))

到此为止我们的数据全部处理好了。接下来我们就要开始建模了。

构建模型:

from torch import nn


class HousePriceModel(nn.Module):

    def __init__(self, input_size) -> None:
        super().__init__()
        self.output = nn.Linear(input_size, 1)  # 10, 1

    def forward(self, x):
        return self.output(x)


model = HousePriceModel(X_train_tensor.shape[-1])
model.to(device)

结果:

HousePriceModel(
  (output): Linear(in_features=10, out_features=1, bias=True)
)

查看模型总参数:

total_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print('模型总参数：', total_params)

结果:

模型总参数： 11

构建损失函数MSE:

criterion = nn.MSELoss()  # 回归-MSE

构建优化器:

from torch import optim

optimizer = optim.SGD(model.parameters(), lr=0.0005)

我们准备开始训练:

num_epochs = 1500

train_losses = []
test_losses = []

patience = 150  # 早停耐心值，如果验证的损失在150次训练中都没有提升，则停止训练
best_val_loss = float('inf')  # 初始化无穷大, 记录模型最佳状态的损失值

best_model_path = r'./models/best_housing_model01.pth'

这里面我们可以自由的去定义训练次数, train_losses和test_losses分别记录训练和测试的损失。

如果训练次数超过一定次数(比如150次)结果AI还没有提示的话, 那就停止训练, 因为一直不提示继续训练的话, 很容易导致AI训练过拟合。

开始训练并且评估模型:

for epoch in range(num_epochs):
    model.train()
    epoch_loss = 0  # 每个epoch的损失 每个批次的总损失
    for batch_X, batch_y in train_loader:

        # 对每个批次进行训练
        y_pred = model(batch_X)

        loss = criterion(y_pred, batch_y)
        epoch_loss += loss.item()

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    avg_train_loss = epoch_loss / len(train_loader)
    train_losses.append(avg_train_loss)

    model.eval()
    with torch.no_grad():
        y_pred_all = model(X_test_tensor)
        val_loss = criterion(y_pred_all, y_test_tensor)
        test_losses.append(val_loss.item())

    if (epoch + 1) % 10 == 0:
        print(
            f"Epoch {epoch+1}/{num_epochs}, Train Loss: {avg_train_loss:.4f}, Test Loss: {val_loss:.4f}"
        )

    if val_loss < best_val_loss:
        best_val_loss = val_loss
        counter = 0  # 重置计数器
        # 保存模型参数
        torch.save(model.state_dict(), best_model_path)
        print(f"Best model saved at Epoch {epoch+1}")
    else:
        # 本次训练没有提升
        counter += 1  # 累计没有提升的次数
        if counter >= patience:
            print(f"Early stopping at Epoch {epoch+1}")
            break

运行结果:

Best model saved at Epoch 1
Best model saved at Epoch 2
Best model saved at Epoch 3
Best model saved at Epoch 4
Best model saved at Epoch 5
Best model saved at Epoch 6
Best model saved at Epoch 7
Best model saved at Epoch 8
Best model saved at Epoch 9
Epoch 10/1500, Train Loss: 0.4296, Test Loss: 0.4240
Best model saved at Epoch 10
Best model saved at Epoch 11
Best model saved at Epoch 12
Best model saved at Epoch 13
Best model saved at Epoch 14
Best model saved at Epoch 15
Best model saved at Epoch 16
Best model saved at Epoch 17
Best model saved at Epoch 18
Best model saved at Epoch 19
Epoch 20/1500, Train Loss: 0.3821, Test Loss: 0.3601
Best model saved at Epoch 20
Best model saved at Epoch 21
Best model saved at Epoch 22
Best model saved at Epoch 23
...
Epoch 890/1500, Train Loss: 0.2338, Test Loss: 0.2181
Epoch 900/1500, Train Loss: 0.2338, Test Loss: 0.2181
Epoch 910/1500, Train Loss: 0.2347, Test Loss: 0.2182
Early stopping at Epoch 919
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...

这里面模型训练到919次的时候, 就停止训练了, 说明这个模型, 其实还可以进一步的提升优化, 至于怎么去优化, 这个问题就留给大家去研究了。(小tips: 可以用激活函数ReLU, Relu的算法是0和x之间取较大值, 还可以用多层线性层, 增加参数量, 再加上隐藏层, 包括丢弃神经元, 调整学习率超参数等方法)。

接下来我们对训练和测试的误差结果进行画图:

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()
plt.figure(figsize=(10, 6))
plt.plot(train_losses, label='Train Loss')  # x轴是训练的轮次，y轴是对应轮次的对应损失
plt.plot(test_losses, label='Val Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.show()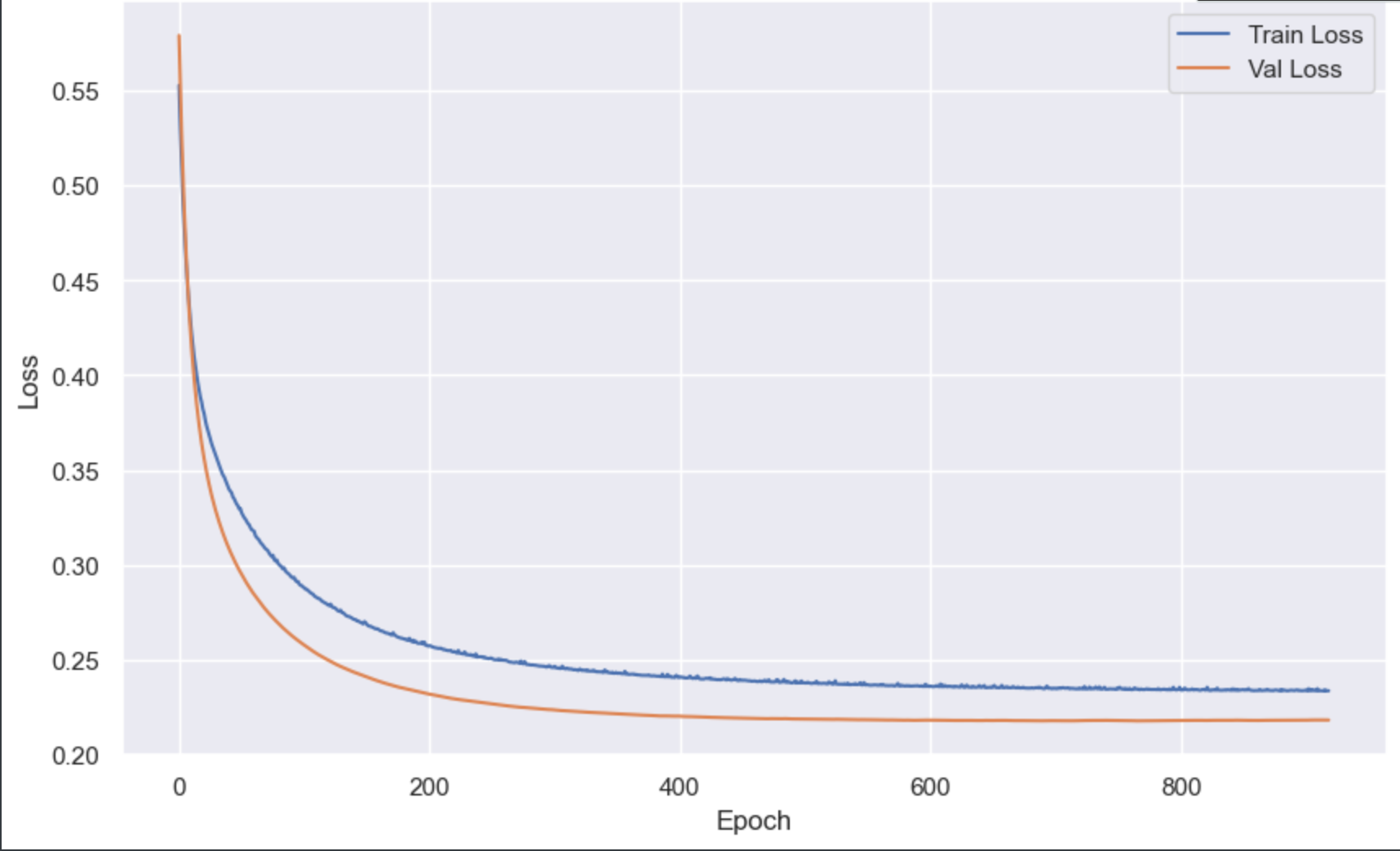

我们取预测和真实值的前10条数据:

y_pred_all[:10], y_test_tensor[:10]

结果:

(tensor([[-0.3749],
         [ 1.4291],
         [-0.8672],
         [-0.2203],
         [ 1.3999],
         [-1.6004],
         [ 0.4435],
         [-0.1592],
         [-1.6152],
         [-0.6918]], device='cuda:0'),
 tensor([[-0.3327],
         [ 1.8142],
         [-0.8301],
         [-0.2760],
         [ 1.6946],
         [-1.3275],
         [ 1.6443],
         [-0.4397],
         [-1.2141],
         [-0.5719]], device='cuda:0'))

由于这些数据是被标准化过的, 我们不太看得懂, 所以我们要进行反标准化。

Y_pred_inverse = Y_trandard.inverse_transform(y_pred_all.cpu().numpy())
Y_test_inverse = Y_trandard.inverse_transform(y_test_tensor.cpu().numpy())
Y_pred_inverse[:10], Y_test_inverse[:10]

运行结果:

(array([[151149.44 ],
        [294416.6  ],
        [112048.484],
        [163424.52 ],
        [292097.28 ],
        [ 53823.367],
        [216143.14 ],
        [168278.66 ],
        [ 52646.742],
        [125980.664]], dtype=float32),
 array([[154500.],
        [325000.],
        [115000.],
        [159000.],
        [315500.],
        [ 75500.],
        [311500.],
        [146000.],
        [ 84500.],
        [135500.]], dtype=float32))

我们再画一张关于Ai预测的结果和真实结果的对比图:

plt.figure(figsize=(10, 6))
plt.scatter(Y_test_inverse, Y_pred_inverse, alpha=0.5)
plt.plot([min(Y_test_inverse), max(Y_test_inverse)],
         [min(Y_test_inverse), max(Y_test_inverse)],
         color='red',
         linewidth=2)
plt.xlabel('Actual SalePrice')
plt.ylabel('Predicted SalePrice')
plt.title('Actual vs Predicted SalePrice')
plt.grid(True)
plt.show()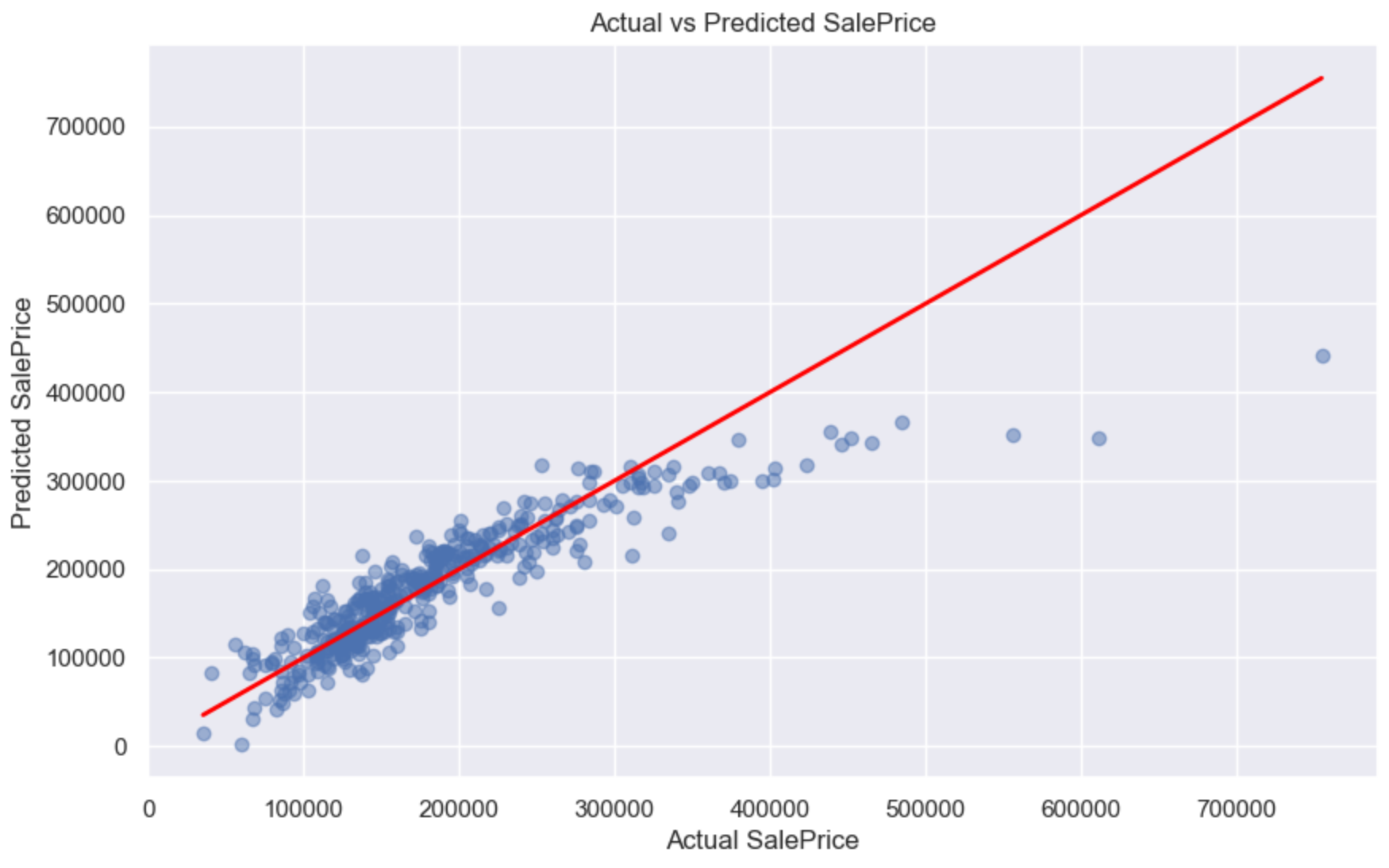

我们可以看到, 那条红线是AI预测出来的结果, 而那些蓝色的小点, 就是房子的真实价格, 由于房价受到多因素影响, 所以算法肯定没线性回归那门简单, 需要考虑到多因素条件, 所以这里面测出来, 有些房价预测的比较偏, 是正常的。

二、深度学习的概念

生物学

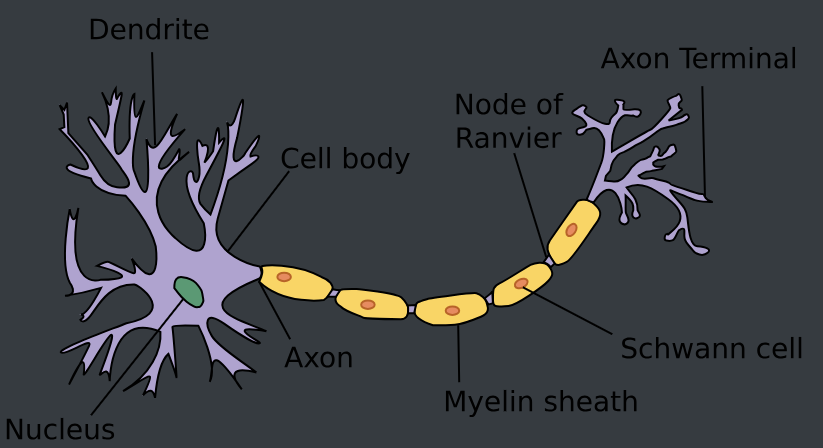
这是一张由树突（dendrites，输入终端）、 细胞核（nucleus，CPU）组成的生物神经元图片。 轴突（axon，输出线）和轴突端子（axon terminal，输出端子） 通过突触（synapse）与其他神经元连接。

树突中接收到来自其他神经元（或视网膜等环境传感器）的信息xix_ixi。 该信息通过突触权重wiw_iwi来加权，以确定输入的影响（即，通过xiwix_iw_ixiwi相乘来激活或抑制）。 来自多个源的加权输入以加权和y=∑ixiwi+by=∑_ix_iw_i+by=∑ixiwi+b的形式汇聚在细胞核中，然后将这些信息发送到轴突yyy中进一步处理，通常会通过σ(y)σ(y)σ(y)进行一些非线性处理。 之后，它要么到达目的地（例如肌肉），要么通过树突进入另一个神经元。

当然，许多这样的单元可以通过正确连接和正确的学习算法拼凑在一起， 从而产生的行为会比单独一个神经元所产生的行为更有趣、更复杂， 这种想法归功于我们对真实生物神经系统的研究。

线性模型可以很好的解释这部分，所有我们将线性模型作为起点，将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。

但是当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。虽然飞机可能受到鸟类的启发，但几个世纪以来，鸟类学并不是航空创新的主要驱动力。 同样地，如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。

多层感知机

线性意味着单调假设： 任何特征的增大都会导致模型输出的增大（如果对应的权重为正）， 或者导致模型输出的减小（如果对应的权重为负）。

我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。

这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP

多层感知机就是深度网络中的一种。多层感知机由多层神经元组成， 每一层与它的上一层相连，从中接收输入； 同时每一层也与它的下一层相连，影响当前层的神经元。

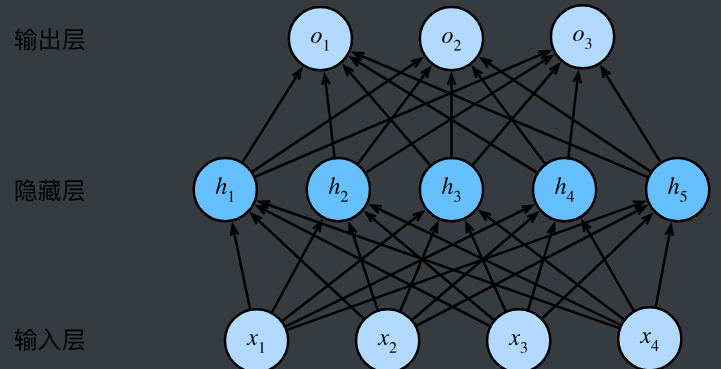
这个多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。 输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。 因此，这个多层感知机中的层数为2。 注意，这两个层都是全连接的。 每个输入都会影响隐藏层中的每个神经元， 而隐藏层中的每个神经元又会影响输出层中的每个神经元。

在添加隐藏层之后，模型现在需要跟踪和更新额外的参数。 可我们能从中得到什么好处呢？在上面定义的模型里，我们没有好处！ 原因很简单：上面的隐藏单元由输入的仿射函数给出， 而输出（softmax操作前）只是隐藏单元的仿射函数。 仿射函数的仿射函数本身就是仿射函数， 但是我们之前的线性模型已经能够表示任何仿射函数。

仿射函数是线性函数的一种扩展，它在线性函数的基础上增加了一个常数项（偏置项）表示平移。其数学表达式为：
y=wx+by = wx + by=wx+b

其中，xxx是输入，www是权重，bbb是偏置项，yyy是输出。

通过引入偏置项使其更灵活，广泛应用于需要建模线性关系但允许平移的场景（如深度学习、回归分析等）。其核心思想是：先进行线性变换，再进行平移

我们可以证明这一等价性
O=(XW(1)+b(1))W(2)+b(2)=XW(1)W(2)+b(1)W(2)+b(2)=XW+b.\mathbf{O} = (\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W} + \mathbf{b}.O=(XW(1)+b(1))W(2)+b(2)=XW(1)W(2)+b(1)W(2)+b(2)=XW+b.

为了发挥多层架构的潜力， 我们还需要一个额外的关键要素： 在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）σ\sigmaσ。 激活函数的输出（例如，σ(⋅)\sigma(\cdot)σ(⋅)）被称为活性值（activations）。 一般来说，有了激活函数，就不可能再将我们的多层感知机退化成线性模型，因为激活函数引入了非线性变换就无法展开简化了。

线性系统以其简单性和可解性成为科学研究的基础工具，适用于描述近似均匀、稳定的现象。

非线性系统则是现实世界的常态，能刻画复杂、动态、非均匀的现象（如生命系统、金融市场波动），但其分析和求解更具挑战性。

激活函数

激活函数（activation function）是神经网络中用于引入非线性变换的重要组成部分。

激活函数的作用是在神经网络的隐藏层中引入非线性变换，使得模型能够学习和表示更复杂的模式和关系。

Sigmoid

Sigmoid函数是一种常用的激活函数，其数学表达式为：
f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}f(x)=1+e−x1

Sigmoid函数的取值范围为(0, 1)，适用于二分类问题。Sigmoid函数将输入映射到一个"概率"范围，使得较小的输入靠近 0，较大的输入接近 1。

Sigmoid函数的导数为：
f′(x)=f(x)×(1−f(x))f'(x) = f(x) \times (1 - f(x))f′(x)=f(x)×(1−f(x))

Sigmoid函数的优点：

• 输出值在(0, 1)之间，便于解释概率。在输出层使用Sigmoid将结果映射到 [0,1] 的概率区间，适合二分类输出（如逻辑回归、二元分类神经网络的输出层）。由于其输出是一个概率值，Sigmoid适用于需要概率值的场景。
• 导数连续，便于反向传播。

Sigmoid函数的缺点：

• 对于较大的正值和负值，Sigmoid的导数趋于 0，会导致梯度消失问题。
• 输出不是0均值，导致收敛速度慢。

应用场景：

• 二分类任务：在输出层使用Sigmoid将结果映射到 [0,1] 的概率区间，适合二分类输出（如逻辑回归、二元分类神经网络的输出层）。
• 概率建模：由于其输出是一个概率值，Sigmoid适用于需要概率值的场景。

Tanh

Tanh函数是一种常用的激活函数，其数学表达式为：
f(x)=ex−e−xex+e−xf(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}f(x)=ex+e−xex−e−x

Tanh与Sigmoid类似，但其输出为对称的 S 型曲线，更适合处理中心化的数据。

Tanh函数的取值范围为(-1, 1)，适用于多分类问题。

Tanh函数的导数为：
f′(x)=1−f(x)2f'(x) = 1 - f(x)^2f′(x)=1−f(x)2

Tanh函数的优点：

• 输出值在(-1, 1)之间，值域对称：输出在 -1 到 1 之间，比Sigmoid更适合于数据归一化。
• 导数连续，便于反向传播。
  Tanh函数的缺点：
• 饱和区问题：Tanh在极大和极小值处，梯度也趋于 0，存在梯度消失问题。
• 输出不是0均值，导致收敛速度慢。

应用场景：

• 隐藏层：Tanh常用于隐藏层的激活函数，比Sigmoid更适合因为其值域包含负值，数据更加平衡。
• 情感分析或文本分类：在自然语言处理等需要处理正负情绪的数据时，Tanh的对称性使其在表示负相关信息时更加自然。

ReLU

ReLU函数是一种常用的激活函数，其数学表达式为：
f(x)=max(0,x)f(x) = max(0, x)f(x)=max(0,x)

将负数直接置为 0，正数不变。ReLU是目前最常用的激活函数。

ReLU函数的优点：

• 计算效率高：ReLU函数简单且计算快速。。
• 梯度不饱和：ReLU在正数区域的梯度恒定为 1，有助于解决梯度消失问题。
  ReLU函数的缺点：
• 死亡"现象：当神经元的输入总是负数时，ReLU的输出恒为 0，此神经元可能"死亡"

应用场景：

• 隐藏层的激活函数：ReLU几乎是所有卷积神经网络和深度前馈网络中隐藏层的默认选择。
• 大多数深度神经网络的隐藏层：ReLU的特性使其适合构建较深的网络，特别是在图像分类、对象检测等任务中。

Leaky ReLU

Leaky ReLU函数是一种常用的激活函数，其数学表达式为：
f(x)=max(0.01x,x)f(x) = max(0.01x, x)f(x)=max(0.01x,x)

解决 ReLU 的 "神经元死亡" 问题。

Softmax

Softmax函数是一种常用的激活函数，其数学表达式为：
f(xi)=exi∑j=1nexjf(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}f(xi)=∑j=1nexjexi

Softmax将一组输入值归一化为概率分布，每个输出值都在 [0,1] 之间且所有输出之和为 1。

Softmax函数的优点：

• 输出值在(0, 1)之间，便于解释概率。
• 概率输出：Softmax函数将所有值压缩在 [0,1] 内，并保证所有输出和为 1，适合多分类问题。
• 相对比较性：Softmax函数在概率分配中考虑了每个类别的相对大小，适合输出一组概率。

应用场景：

• 多分类任务的输出层：Softmax在多分类问题中广泛应用，特别是在图像分类、文本分类等任务中，用于输出多个类别的概率值。
• 分类任务中对类别的重要性建模：Softmax输出的概率分布，可以用来确定模型对于不同类别的置信度。

看任务类型：

• 二分类任务：Sigmoid
• 多分类任务：Softmax
• 隐藏层：优先用ReLU，出现负数很多的情况，ReLU不行换Leaky ReLU

看数据特性：

• 大量负数 Leaky ReLU
• 如果数据[-1,1] Tanh
• 其他ReLU

时效：

• 实时推理系统 ReLU

输入层

隐藏层：ReLU 默认首选，Leaky ReLU 替补

输出层：二分类Sigmoid，多分类Softmax，生成任务Tanh

以上就是关于深度学习的概念部分, 我们可以通过画图的方式, 来进行对比。

我们先生成10个数据, 我们之后画的所有的图, 都是基于这个数据来画图:

import torch

x = torch.linspace(-100, 100, 10)
x

结果:

tensor([-100.0000,  -77.7778,  -55.5556,  -33.3333,  -11.1111,   11.1111,
          33.3333,   55.5556,   77.7778,  100.0000])

准备导入画图库并画图:

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()

我们画关于Sigmoid函数的图像

from sympy.printing.pretty.stringpict import line_width
from torch import nn

plt.figure(figsize=(10, 6))
y = nn.Sigmoid()(x)
plt.plot(x, y, linewidth=2.5, color='royalblue')
plt.axhline(y=0, color='grey', linewidth=1.0, linestyle='--')
plt.axvline(x=0, color='grey', linewidth=1.0, linestyle='--')
plt.show()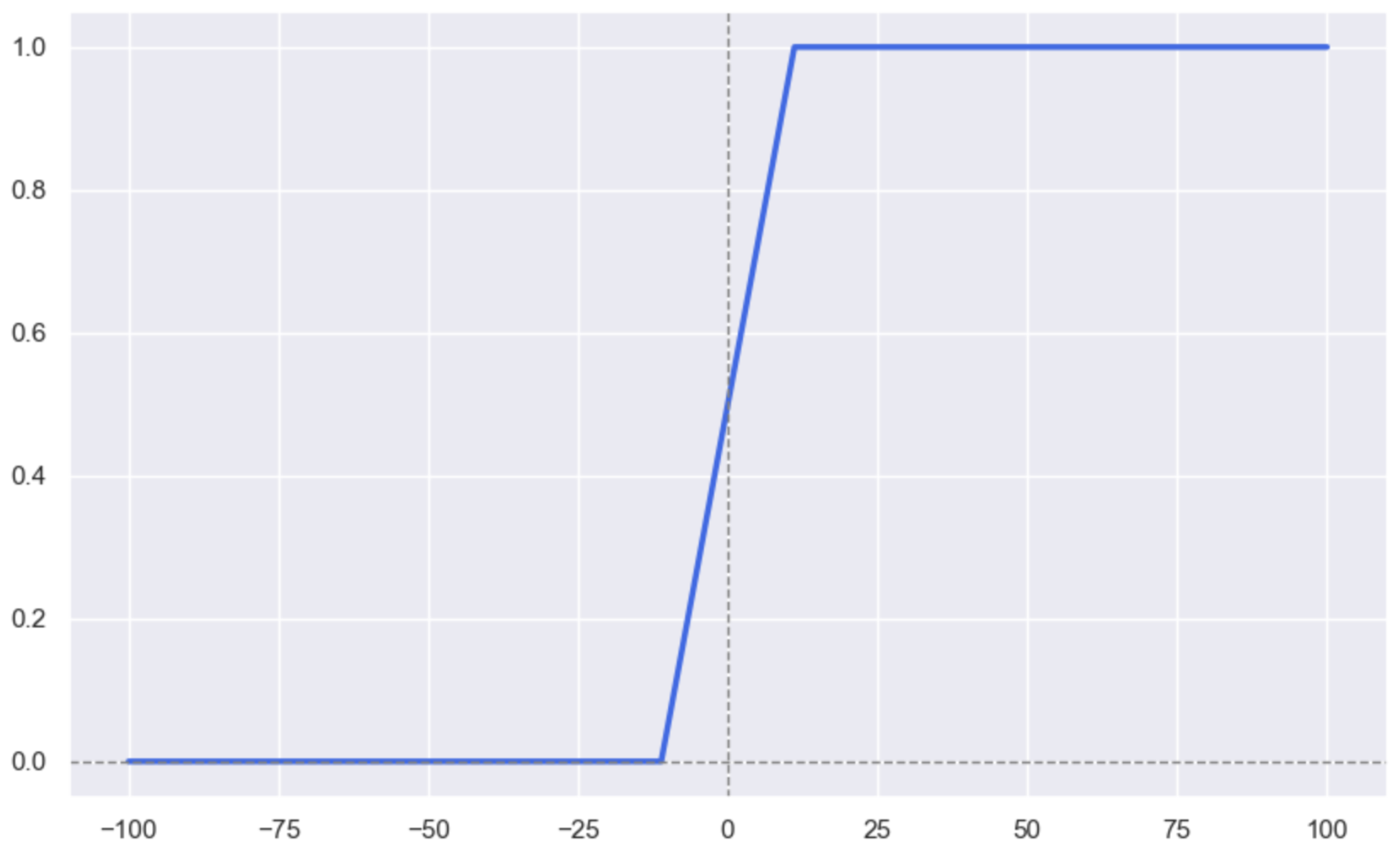

我们再画关于双曲正切函数的图像:

plt.figure(figsize=(10, 6))
y = nn.Tanh()(x)
plt.plot(x, y, linewidth=2.5, color='royalblue')
plt.axhline(y=0, color='grey', linewidth=1.0, linestyle='--')
plt.axvline(x=0, color='grey', linewidth=1.0, linestyle='--')
plt.show()

结果:

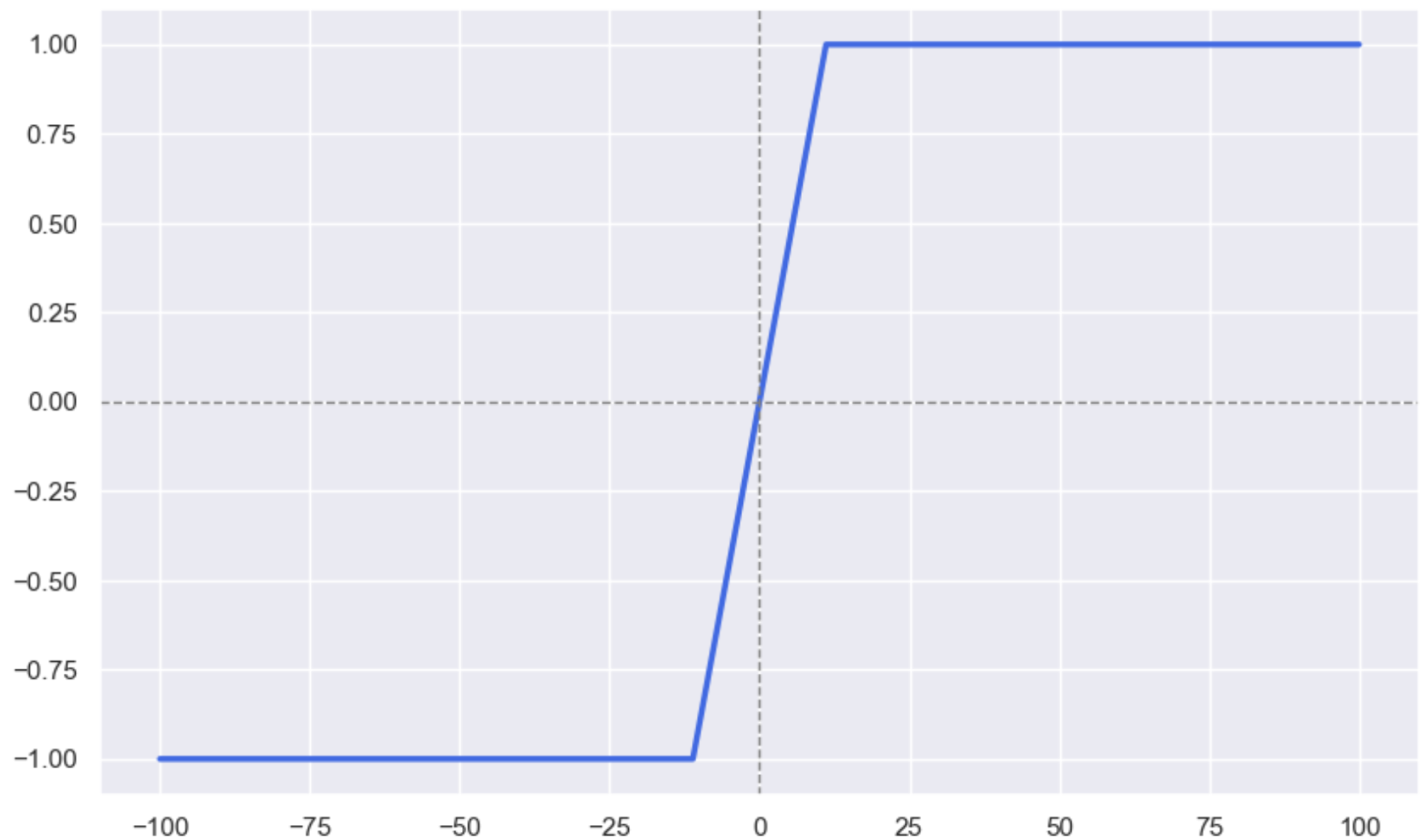
我们可以看到, Sigmoid函数和Tanh函数, 图像的形状画出来是一样的, 但是因变量的范围不同, Sigmoid函数求出来的因变量范围在0到1之间, 而双曲正切函数的因变量范围在-1到1之间。

我们再画关于ReLU函数的图像:

plt.figure(figsize=(10, 6))
y = nn.ReLU()(x)
plt.plot(x, y, linewidth=2.5, color='royalblue')
plt.axhline(y=0, color='grey', linewidth=1.0, linestyle='--')
plt.axvline(x=0, color='grey', linewidth=1.0, linestyle='--')
plt.show()

结果:

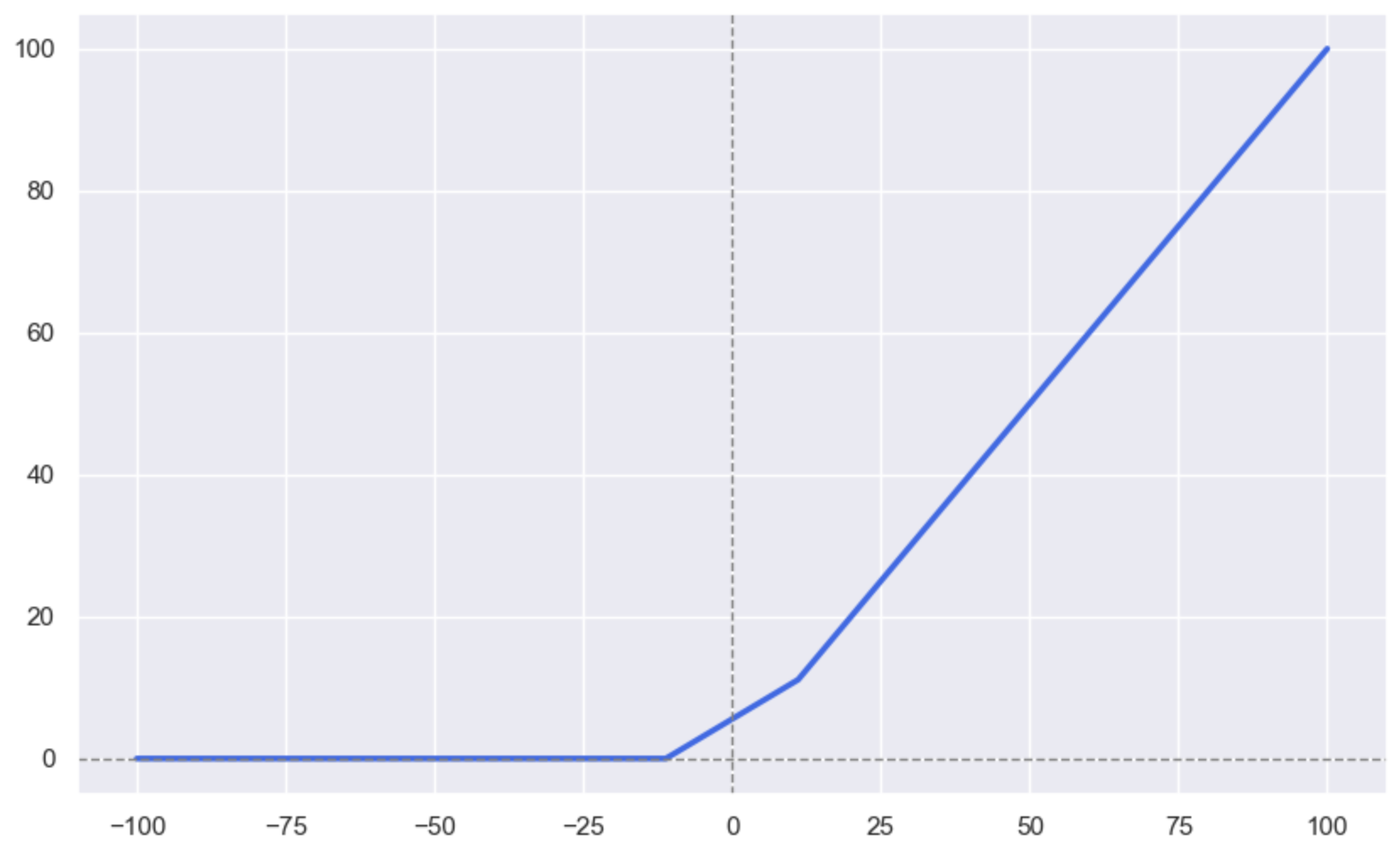
接着我们画LeakyReLU函数的图像:

plt.figure(figsize=(10, 6))
y = nn.LeakyReLU()(x)
plt.plot(x, y, linewidth=2.5, color='royalblue')
plt.axhline(y=0, color='grey', linewidth=1.0, linestyle='--')
plt.axvline(x=0, color='grey', linewidth=1.0, linestyle='--')
plt.show()

运行结果:

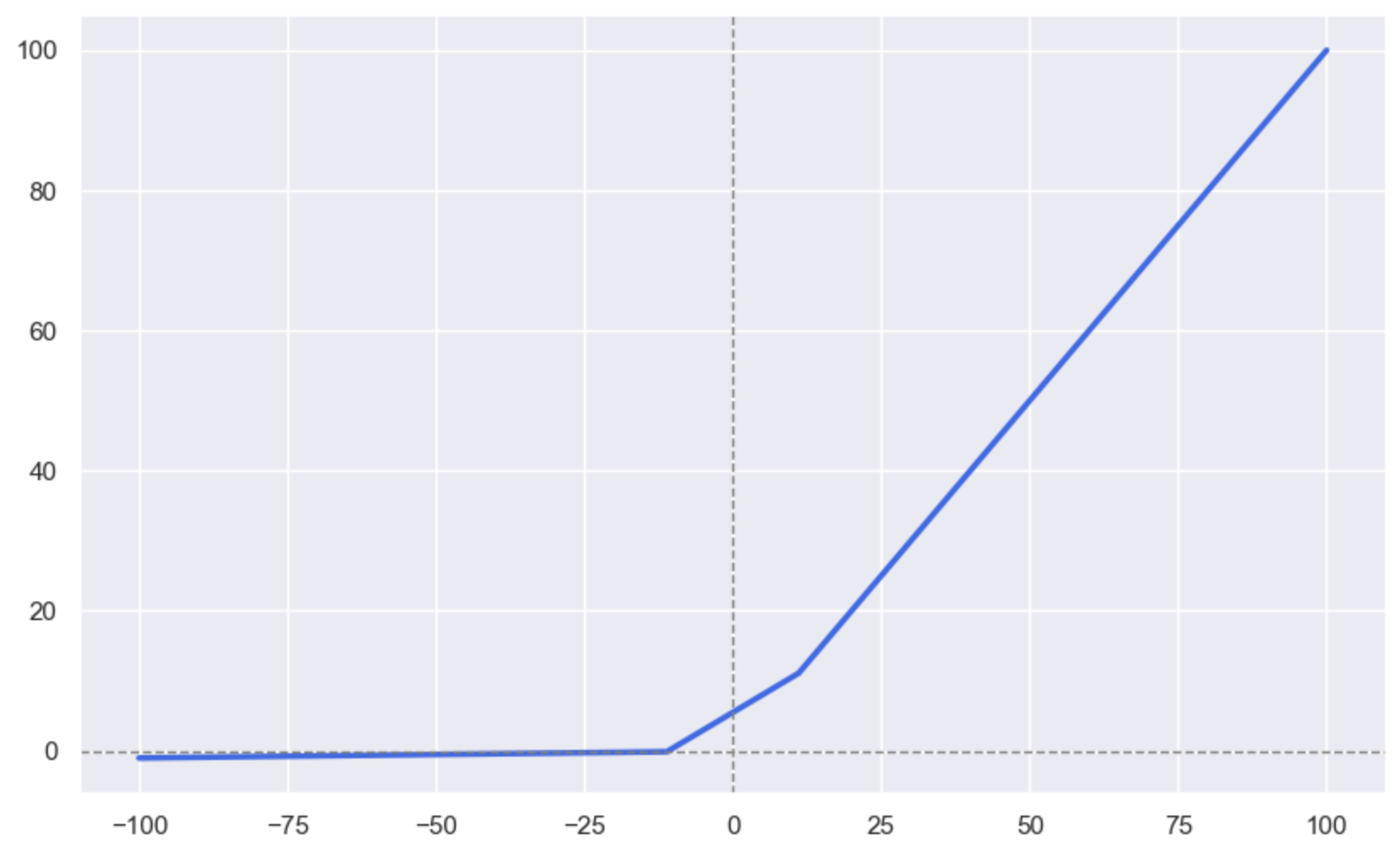
两张图看上去非常相似, 但是有一点不同, 那就是它们的算法有一点儿区别。

区别:

ReLU激活函数的算法: f(x)=max(0,x)f(x) = max(0, x)f(x)=max(0,x)

Leaky ReLU激活函数的算法: f(x)=max(0.01x,x)f(x) = max(0.01x, x)f(x)=max(0.01x,x)

所以Leaky ReLU函数画出来的图, 最左边会有负数的情况。

总结:

本篇文章完成了上一篇文章留下来的房价预测的问题, 并且讲述了关于深度学习的理论知识, 最后面讲解了四个函数的图像, 分别是

• Sigmoid函数

• Tanh函数（双曲正切）

• ReLU函数

• LeakyReLU函数

好了, 这篇文章关于深度学习的内容就到此结束了。

以上就是深度学习的所有内容了, 如果有哪里不懂的地方,可以把问题打在评论区, 欢迎大家在评论区交流!!!

如果我有写错的地方, 望大家指正, 也可以联系我, 让我们一起努力, 继续不断的进步.

学习是个漫长的过程, 需要我们不断的去学习并掌握消化知识点, 有不懂或概念模糊不理解的情况下,一定要赶紧的解决问题, 否则问题只会越来越多, 漏洞也就越老越大.

人生路漫漫, 白鹭常相伴!!!