蓝桥云课-5. 花灯调整【算法赛】

题目：

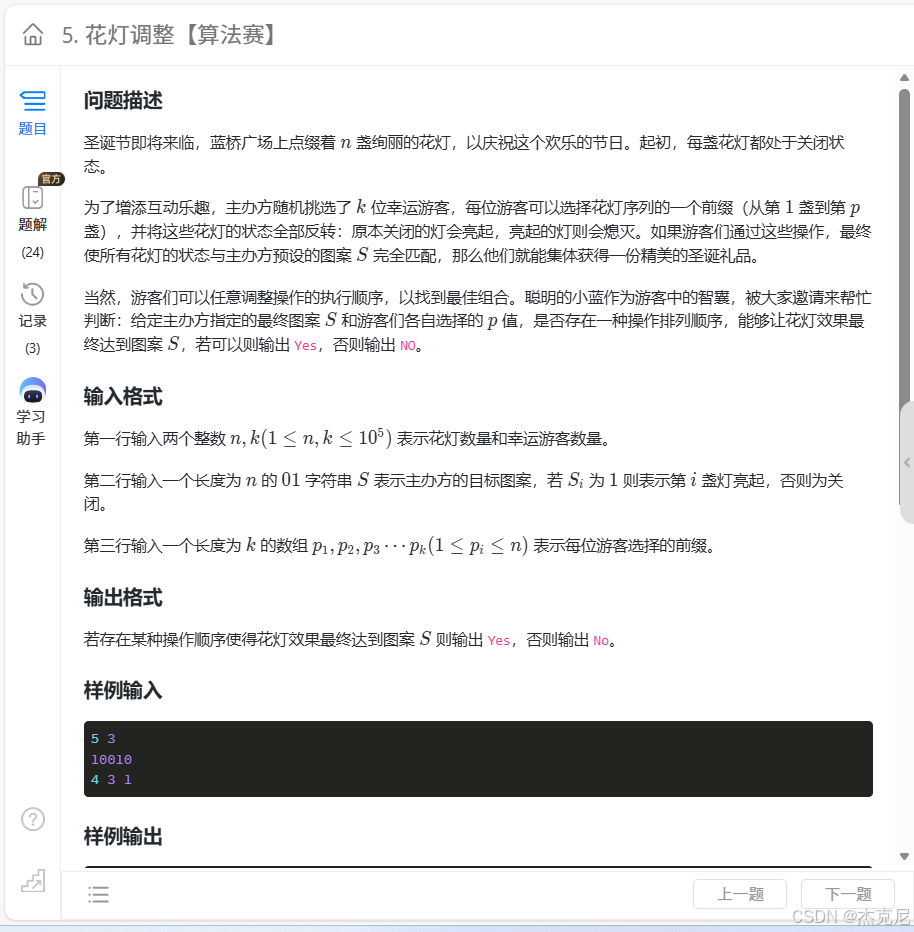
解题思路：

从前往后统计其后缀和，最后判断与当前位置翻转是否相同即可(偶数相当于没有翻转,奇数翻转)

代码：

java 复制代码

 /*out
*Stack Integer ArrayList String StringBuffer peek
*Collections imports LinkedList offer return
*empty polls offerLast pollFirst isEmpty
*List Deque append length HashMap
*return remove boolean continue charAt
*toString static System println nextInt
*Scanner  System  toCharArray contains
*/
import java.util.*;
public class Main {
    static Scanner sc = new Scanner(System.in);
    public static void main(String[] args) {
        int t=1;
        while(t--!=0){
          slove();
        }
        sc.close();
    }
    public static void slove(){
      int n=sc.nextInt(),k=sc.nextInt();
      String s=sc.next();
      int [] p=new int[n];
      for(int i=0;i<k;i++){
        p[sc.nextInt()-1]++;
      }
      int[] ciShu=new int[n];
      ciShu[n-1]=p[n-1];
      for(int i=n-2;i>=0;i--){
        ciShu[i]=p[i]+ciShu[i+1];
      }
      char[] tar=s.toCharArray();
      for(int i=0;i<tar.length;i++){
        int a=tar[i]-'0';
        if(a%2!=ciShu[i]%2){
          System.out.println("No");
          return ;
        }
      }
      System.out.println("Yes");
    }
}

问题:

总结：

【算法解析】后缀和解决 "花灯调整" 策略判定问题：从问题本质到代码实现

在算法竞赛中，"操作叠加的状态判定"类问题是高频考点之一 ------ 这类问题的核心是 "操作的顺序不影响最终状态，仅与操作次数的奇偶性有关"。本文以 "花灯调整" 问题为例，从问题拆解、核心规律、后缀和原理、代码实现等维度，全面讲解如何用后缀和高效解决这类问题，同时深入剖析代码的每一个细节，帮助你掌握这类问题的通用解法。

一、问题背景与需求拆解

在开始代码分析前，我们先彻底理解问题的规则与目标，这是后续算法设计的基础。

1.1 问题规则

初始状态：n盏花灯，全部处于关闭状态（用 0 表示）；

游客操作：每位游客选择一个 "前缀p"（即从第 1 盏到第p盏灯的连续区间），将该区间内所有花灯的状态反转（0 变 1，1 变 0）；

目标状态：给定一个长度为n的 01 字符串S，其中S[i]表示第i+1盏灯的目标状态（S[i]='1'表示亮，S[i]='0'表示灭）；

操作顺序：游客可以任意调整操作的执行顺序；

问题目标：判断是否存在一种操作顺序，使得最终所有花灯的状态与目标串S完全一致。

1.2 需求转化为数学模型

我们的核心任务是：

验证 "游客操作对每盏灯的反转次数的奇偶性" 是否恰好等于 "从初始状态（0）到目标状态（S[i]）所需的反转次数的奇偶性"。

原因很简单：

反转操作是幂等的（反转偶数次等价于未反转，反转奇数次等价于反转 1 次）；

操作顺序不影响最终状态（因为反转是 "叠加" 的，先反转前 3 盏再反转前 5 盏，与先反转前 5 盏再反转前 3 盏，每盏灯的反转次数完全相同）。

二、核心规律：反转次数的统计与后缀和的应用

要解决问题，首先需要明确每盏灯的反转次数如何计算------ 这是问题的关键突破口。

2.1 每盏灯的反转次数的定义

对于第i盏灯（索引从 0 开始），它的反转次数 = 选择了 "前缀p ≥ i+1" 的游客数量之和（因为游客选前缀p时，会反转前p盏灯，第i盏灯属于前p盏的条件是p ≥ i+1）。

举个例子：

第 0 盏灯（对应实际第 1 盏）的反转次数 = 选了p≥1的游客数量之和；

第 2 盏灯（对应实际第 3 盏）的反转次数 = 选了p≥3的游客数量之和。

2.2 为什么用 "后缀和" 统计反转次数

统计 "选了p ≥ x的游客数量之和"，本质是对 "游客选择的前缀数组" 做 "从 x 到末尾的累加"------ 这正是后缀和的典型应用场景：

前缀和：从左到右累加，统计 "前 x 项的和"；

后缀和：从右到左累加，统计 "从 x 到末尾的和"。

因此，我们可以用后缀和快速计算每盏灯的反转次数，时间复杂度为O(n)，完全满足n ≤ 10^5的规模要求。

三、代码整体结构解析

我们先从宏观上看代码的模块划分，理解代码是如何对应问题需求的：

java

运行

import java.util.*;

public class Main {

static Scanner sc = new Scanner(System.in);

public static void main(String[] args) {

int t=1;

while(t--!=0){ // 兼容多组测试用例（此处t=1，仅执行1次）

slove();

}

sc.close();

}

public static void slove(){

// 1. 输入读取与初始化

int n=sc.nextInt(),k=sc.nextInt();

String s=sc.next();

int [] p=new int[n];

for(int i=0;i<k;i++){

p[sc.nextInt()-1]++;

}

// 2. 计算每盏灯的反转次数（后缀和）

int[] ciShu=new int[n];

ciShu[n-1]=p[n-1];

for(int i=n-2;i>=0;i--){

ciShu[i]=p[i]+ciShu[i+1];

}

// 3. 对比反转次数的奇偶性与目标状态

char[] tar=s.toCharArray();

for(int i=0;i<tar.length;i++){

int a=tar[i]-'0';

if(a%2!=ciShu[i]%2){

System.out.println("No");

return ;

}

// 4. 输出结果

System.out.println("Yes");

}

代码分为 4 个核心模块：

输入读取模块：将输入的 "前缀选择" 统计到数组中；

后缀和计算模块：用后缀和得到每盏灯的反转次数；

奇偶性对比模块：验证反转次数的奇偶性是否匹配目标状态；

输出模块：根据验证结果输出 "Yes" 或 "No"。

四、输入读取模块：结构化存储游客的选择

输入处理是算法题的基础，结构化存储能避免后续逻辑中 "变量混淆" 的问题，我们详细解析这部分代码的设计思路。

4.1 输入的对应关系

问题的输入分为三部分：

第一行：n（花灯数）、k（游客数）；

第二行：目标串S（长度为n的 01 字符串）；

第三行：k个整数p_1~p_k（每位游客选择的前缀）。

4.2 代码的输入处理逻辑

java

运行

// 读取n和k

int n=sc.nextInt(),k=sc.nextInt();

// 读取目标串s

String s=sc.next();

// 定义数组p：p[x]表示"选择了前缀x+1的游客数量"（x是0-based索引）

int [] p=new int[n];

for(int i=0;i<k;i++){

// 游客输入的p是1-based（比如选前缀3对应实际第3盏），转为0-based索引

int choose = sc.nextInt() - 1;

p[choose]++;

}

关键细节：

游客输入的 "前缀p" 是1-based（比如选 "前缀 3" 表示前 3 盏灯），而代码中数组是0-based（索引 0 对应实际第 1 盏），因此需要sc.nextInt() - 1将输入转为数组索引；

数组p的含义：p[x]表示 "选择了前缀x+1的游客数量"（比如p[2]表示选了前缀 3 的游客数）。

4.3 样例输入的存储结果

以样例输入为例：

plaintext

样例输入：

5 3

10010

4 3 1

n=5，k=3，目标串s="10010"；

游客选择的前缀是 4、3、1，转为 0-based 索引是 3、2、0；

数组p的结果：p[0]=1（选前缀 1 的游客数）、p[2]=1（选前缀 3 的游客数）、p[3]=1（选前缀 4 的游客数），其余为 0 → p = [1,0,1,1,0]。

五、后缀和计算模块：核心逻辑的实现

这是代码的灵魂部分 ------ 用后缀和计算每盏灯的反转次数，我们从原理、代码、样例验证三个维度详细解析。

5.1 后缀和的原理回顾

后缀和的定义是：

对于数组arr，后缀和数组suffixSum满足：suffixSum[i] = arr[i] + suffixSum[i+1]（从右到左计算）。

对于我们的问题，数组p存储了 "每个前缀被选择的次数"，因此：

第i盏灯（0-based）的反转次数 = p[i] + p[i+1] + ... + p[n-1] → 这正是后缀和数组suffixSum[i]的值。

5.2 后缀和的代码实现

java

运行

// 定义ciShu数组：ciShu[i]表示第i盏灯的反转次数

int[] ciShu=new int[n];

// 初始化最后一盏灯的反转次数（只有选了前缀n的游客会影响它）

ciShu[n-1]=p[n-1];

// 从倒数第二盏灯往前计算后缀和

for(int i=n-2;i>=0;i--){

ciShu[i] = p[i] + ciShu[i+1];

}

代码逻辑拆解：

最后一盏灯（i=n-1）的反转次数 = 选了前缀n的游客数（即p[n-1]）；

第i盏灯的反转次数 = 选了前缀i+1的游客数（p[i]） + 第i+1盏灯的反转次数（因为选前缀≥i+2的游客也会影响第i盏灯）。

5.3 样例的后缀和计算结果

以样例的p = [1,0,1,1,0]为例：

ciShu[4] = p[4] = 0（最后一盏灯，选前缀 5 的游客数为 0）；

ciShu[3] = p[3] + ciShu[4] = 1 + 0 = 1（第 4 盏灯，选前缀 4 的游客数 + 第 5 盏的反转次数）；

ciShu[2] = p[2] + ciShu[3] = 1 + 1 = 2（第 3 盏灯，选前缀 3 的游客数 + 第 4 盏的反转次数）；

ciShu[1] = p[1] + ciShu[2] = 0 + 2 = 2（第 2 盏灯，选前缀 2 的游客数 + 第 3 盏的反转次数）；

ciShu[0] = p[0] + ciShu[1] = 1 + 2 = 3（第 1 盏灯，选前缀 1 的游客数 + 第 2 盏的反转次数）；

最终ciShu数组（每盏灯的反转次数）为：[3,2,2,1,0]。

六、奇偶性对比模块：判定是否可行的核心

这部分代码的作用是验证 "每盏灯的反转次数的奇偶性" 是否与 "目标状态所需的反转次数的奇偶性" 一致 ------ 这是问题的最终判定条件。

6.1 目标状态与反转次数的奇偶性

初始状态下，所有灯都是 0，要达到目标状态S[i]（0 或 1）：

若S[i] = '0'：不需要反转，或反转偶数次（最终状态为 0）；

若S[i] = '1'：需要反转奇数次（最终状态为 1）。

因此，目标状态所需的反转次数的奇偶性 = S[i] - '0'（将字符转为整数 0 或 1）。

6.2 代码的奇偶性对比逻辑

java

运行

// 将目标串转为字符数组，方便逐位访问

char[] tar = s.toCharArray();

// 遍历每盏灯

for(int i=0;i<tar.length;i++){

// 将字符'0'/'1'转为整数0/1，得到目标所需的奇偶性

int targetParity = tar[i] - '0';

// 计算当前灯反转次数的奇偶性

int actualParity = ciShu[i] % 2;

// 若奇偶性不匹配，直接输出"No"并返回

if(targetParity != actualParity){

System.out.println("No");

return ;

}

6.3 样例的奇偶性对比验证

样例中：

目标串s="10010" → tar = ['1','0','0','1','0']；

目标所需的奇偶性：[1,0,0,1,0]；

实际反转次数的奇偶性（ciShu % 2）：[3%2=1, 2%2=0, 2%2=0, 1%2=1, 0%2=0]；

两者完全一致，因此输出 "Yes"，与样例结果匹配。

七、边界情况与性能分析

在算法题中，边界处理和性能是衡量代码质量的关键指标，我们分析代码在这两方面的表现。

7.1 边界情况的处理

代码能正确处理以下边界情况：

所有灯都是 0：目标所需的奇偶性全为 0，只需验证实际反转次数全为偶数；

所有灯都是 1：目标所需的奇偶性全为 1，只需验证实际反转次数全为奇数；

游客数量为 0：此时所有灯的反转次数为 0，只需目标串全为 0；

游客选择的前缀全为 n：此时所有灯的反转次数等于游客数量，只需验证所有灯的目标奇偶性相同。

7.2 性能分析

代码的时间复杂度为O(n + k)：

输入处理：O(k)（遍历 k 个游客的选择）；

后缀和计算：O(n)（遍历 n 盏灯）；

奇偶性对比：O(n)（遍历 n 盏灯）。

空间复杂度为O(n)：

数组p和ciShu的空间都是O(n)，完全满足n ≤ 10^5的题目限制。

八、代码的优化与拓展

虽然当前代码已经能正确解决问题，但我们可以从可读性、扩展性角度做一些优化，让代码更通用。

8.1 变量名的语义化优化

原代码中ciShu（次数）的变量名不够直观，可优化为reverseCount（反转次数）；p可优化为prefixChooseCount（前缀选择次数）：

java

运行

// 优化后

int[] prefixChooseCount = new int[n];

for(int i=0;i<k;i++){

int choose = sc.nextInt() - 1;

prefixChooseCount[choose]++;

}

int[] reverseCount = new int[n];

reverseCount[n-1] = prefixChooseCount[n-1];

for(int i=n-2;i>=0;i--){

reverseCount[i] = prefixChooseCount[i] + reverseCount[i+1];

}

8.2 兼容多组测试用例

原代码中while(t--!=0)的t=1，仅支持单组测试用例。若要支持多组，只需将t改为sc.nextInt()：

java

运行

public static void main(String[] args) {

int t = sc.nextInt(); // 读取测试用例数

while(t--!=0){

slove();

}

sc.close();

}

8.3 拓展：处理 "反转区间" 的通用问题

这类 "操作区间、统计每点的操作次数" 的问题，都可以用差分 + 前缀和的方式解决（后缀和是前缀和的一种变体）。例如：

若操作是 "反转区间[l, r]"，可以用差分数组记录区间的变化，再用前缀和得到每点的操作次数。

九、总结

本文以 "花灯调整" 问题为例，详细讲解了后缀和在 "操作叠加的状态判定" 类问题中的应用：

问题拆解：将 "状态匹配" 转化为 "反转次数的奇偶性匹配"；

核心规律：操作顺序不影响最终状态，仅与操作次数的奇偶性有关；

算法选择：用后缀和快速统计每盏灯的反转次数，时间复杂度O(n)；

代码实现：输入处理→后缀和计算→奇偶性对比→输出结果，模块清晰。

这类问题的通用解题步骤是：

分析操作对每个元素的影响；

用前缀和 / 后缀和 / 差分统计每个元素的操作次数；

验证操作次数的奇偶性是否匹配目标状态。

掌握这一思路后，你可以轻松解决类似的 "开关灯""翻转字符串" 等问题 ------ 核心是抓住 "操作的幂等性" 和 "区间统计的前缀和 / 后缀和技巧"。