数据结构与算法--008四数之和 与经典子数组 / 子串问题解析

Han.miracle2025-12-20 15:57

008：209. 长度最小的子数组 - 力扣（LeetCode）

暴力解法：

1. 核心思路
  • 排序：先对数组排序，便于后续去重和比较。
  • 四层循环：通过四层嵌套循环遍历所有可能的四元组，计算四数之和是否等于目标值。
  • 哈希去重 ：使用HashSet存储符合条件的四元组，自动去除重复的组合。
2. 代码实现（优化后）
java 复制代码 
package _008;

import java.util.*;

public class _008_force {
    public static void main(String[] args) {
        // 测试用例执行
        Solution solution = new Solution();

        // 测试用例1：基础用例，存在多个四数组合
        int[] nums1 = {-2, -1, -1, 1, 1, 2, 2};
        int target1 = 0;
        List<List<Integer>> result1 = solution.fourSum(nums1, target1);
        System.out.println("测试用例1结果：" + result1);

        // 测试用例2：无符合条件的组合
        int[] nums2 = {1, 2, 3, 4};
        int target2 = 100;
        List<List<Integer>> result2 = solution.fourSum(nums2, target2);
        System.out.println("测试用例2结果：" + result2);

        // 测试用例3：包含重复元素的用例
        int[] nums3 = {2, 2, 2, 2, 2};
        int target3 = 8;
        List<List<Integer>> result3 = solution.fourSum(nums3, target3);
        System.out.println("测试用例3结果：" + result3);

        // 测试用例4：数组长度不足4的情况
        int[] nums4 = {1, 2, 3};
        int target4 = 6;
        List<List<Integer>> result4 = solution.fourSum(nums4, target4);
        System.out.println("测试用例4结果：" + result4);

        // 测试用例5：包含负数和正数的边界用例
        int[] nums5 = {-3, -2, -1, 0, 0, 1, 2, 3};
        int target5 = 0;
        List<List<Integer>> result5 = solution.fourSum(nums5, target5);
        System.out.println("测试用例5结果：" + result5);
    }
}
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        Set<List<Integer>> ret = new HashSet<>();

        if (nums == null || nums.length < 4) {
            return new ArrayList<>();
        }
        Arrays.sort(nums);

        for (int i = 0; i < nums.length - 3; i++) {
            int firstStandard = target - nums[i];
            for (int j = i + 1; j < nums.length - 2; j++) {
                int secondStandard = firstStandard - nums[j];
                for (int k = j + 1; k < nums.length - 1; k++) {
                    for (int l = k + 1; l < nums.length; l++) {
                        if (nums[k] + nums[l] == secondStandard) {
                            ret.add(Arrays.asList(nums[i], nums[j], nums[k], nums[l]));
                        }
                    }
                }
            }
        }
        return new ArrayList<>(ret);
    }
}

方法二：双指针+ 双for循环

1. 核心思路
  • 排序：先对数组排序，为双指针和去重做准备。
  • 双循环 ：外层两层循环遍历前两个数（i和j），并通过跳过重复元素减少无效遍历。
  • 双指针 ：内层使用双指针（left和right）遍历后两个数，通过调整指针位置快速找到和为目标值的组合，同时跳过重复元素去重。
java 复制代码 
package _008;

import java.util.*;

public class _008_first {
    public static void main(String[] args) {
        // 测试用例执行
        Solution3 solution = new Solution3();

        // 测试用例1：基础用例，存在多个四数组合
        int[] nums1 = {-2,-1,-1,1,1,2,2};
        int target1 = 0;
        List<List<Integer>> result1 = solution.fourSum(nums1, target1);
        System.out.println("测试用例1结果：" + result1);

        // 测试用例2：无符合条件的组合
        int[] nums2 = {1, 2, 3, 4};
        int target2 = 100;
        List<List<Integer>> result2 = solution.fourSum(nums2, target2);
        System.out.println("测试用例2结果：" + result2);

        // 测试用例3：包含重复元素的用例
        int[] nums3 = {2, 2, 2, 2, 2};
        int target3 = 8;
        List<List<Integer>> result3 = solution.fourSum(nums3, target3);
        System.out.println("测试用例3结果：" + result3);

        // 测试用例4：数组长度不足4的情况
        int[] nums4 = {1, 2, 3};
        int target4 = 6;
        List<List<Integer>> result4 = solution.fourSum(nums4, target4);
        System.out.println("测试用例4结果：" + result4);

        // 测试用例5：包含负数和正数的边界用例
        int[] nums5 = {-3, -2, -1, 0, 0, 1, 2, 3};
        int target5 = 0;
        List<List<Integer>> result5 = solution.fourSum(nums5, target5);
        System.out.println("测试用例5结果：" + result5);
    }
}

class Solution3 {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums); 
        List<List<Integer>> list = new ArrayList<>();

        
        for (int i = 0; i < nums.length - 3; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;

            int firstTarget = target - nums[i];
            for (int j = i + 1; j < nums.length - 2; j++) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                int secondTarget = firstTarget - nums[j];
                int left = j + 1, right = nums.length - 1;
                while (left < right) {
                    int sum = nums[left] + nums[right];
                    if (sum == secondTarget) {
                        list.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));

                        while (left < right && nums[left] == nums[left + 1]) left++;

                        while (left < right && nums[right] == nums[right - 1]) right--;

                        left++;
                        right--;
                    } else if (sum < secondTarget) {
                        left++;
                    } else {
                        right--;
                    }
                }
            }
        }

        return list;
    }
}
解法 时间复杂度 空间复杂度 优点 缺点
暴力解法 O(n4) O(n) 逻辑简单，易理解 效率极低，空间开销大
双循环 + 双指针 O(n3) O(1) 效率高，剪枝优化 逻辑复杂，需处理边界

009：209. 长度最小的子数组 - 力扣（LeetCode）

方法一：暴力解法

一、核心思路梳理

  1. 外层循环 ：固定子数组的起始位置left。
  2. 内层循环 ：从left开始，不断累加元素到sum，循环的继续条件 是sum < target（累加和未达标）且right < nums.length（未遍历完数组）。
  3. 终止后处理 ：循环终止时，先判断sum是否达标（避免把遍历完数组但和仍不足的情况纳入计算），再更新最小长度。
java 复制代码 
package SlidingWindow;

public class _009_force {

    public static void main(String[] args) {

        // 测试用例1
        int target1 = 7;
        int[] nums1 = {2, 3, 1, 2, 4, 3};
        System.out.println(minSubArrayLen(target1, nums1)); // 输出：2（子数组[4,3]）

        // 测试用例2
        int target2 = 4;
        int[] nums2 = {1, 4, 4};
        System.out.println(minSubArrayLen(target2, nums2)); // 输出：1（子数组[4]）

        // 测试用例3
        int target3 = 11;
        int[] nums3 = {1, 1, 1, 1, 1, 1, 1, 1};
        System.out.println(minSubArrayLen(target3, nums3)); // 输出：0（无符合条件的子数组）
    }

        public static int minSubArrayLen(int target, int[] nums) {
            int minLength = Integer.MAX_VALUE;
            for (int left = 0; left < nums.length; left++) {
                int sum = 0;
                int right = left;
                while(sum < target && right < nums.length){
                    sum +=nums[right];

                    right++;
                }
                if (sum >= target) {
                    // 计算长度：right已经右移，所以是right - left
                    int currentLength = right - left;
                    minLength = Math.min(minLength, currentLength);
                }
                if(minLength > nums.length){
                    return 0;
                }
            }
            return minLength;

    }
}

代码中是先累加nums[right]，再将right++ 。这种顺序导致right最终会指向子数组最后一个元素的下一个位置 ，因此子数组长度是right - left（而非right - left + 1）。

方法二：滑动窗口 又叫做 "同向双指针"

滑动窗口的算法思想：

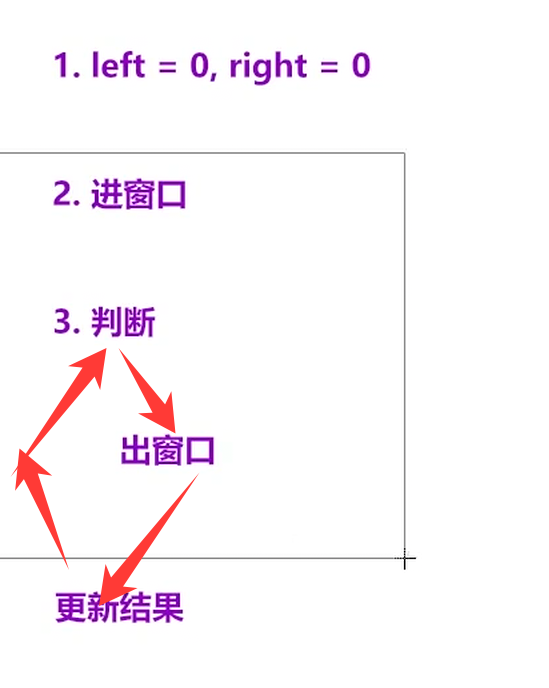
这个顺序没有啥，要具体题目具体分析，这个循环不是固定的，更新结果要因情况而定

以右指针为锚点，找到每个右指针位置下的最短有效窗口，再从这些最短窗口中选出全局最优。：

  1. 子数组是 "连续相邻" 的（这是题目要求，滑动窗口也严格遵循）；
  2. 分阶段选最优，再全局选最优（这是算法的核心优化思路）。
一、滑动窗口介绍

滑动窗口（Sliding Window）是一种常用的双指针技巧，核心思想是通过调整窗口的左右边界（两个指针），在一维数据（如数组、字符串）中维护一个动态的子区间，从而将原本需要嵌套循环的问题（时间复杂度 O (n²)）优化为线性时间复杂度 O (n)。

二、滑动窗口解决 "长度最小的子数组" 问题思路

以 "给定一个含有 n 个正整数的数组和一个正整数 target，找出数组中满足和≥target 的长度最小的连续子数组，并返回其长度。如果不存在，则返回 0" 为例：

  1. 初始化 ：
    • 左指针left：初始化为 0，代表窗口左边界。
    • 当前窗口和current_sum：初始化为 0，记录窗口内元素的和。
    • 最小长度min_len：初始化为无穷大（float('inf')），记录满足条件的最小窗口长度。
  2. 扩展右边界 ：遍历数组，右指针right从 0 到 n-1 依次移动，将nums[right]加入current_sum。
  3. 收缩左边界 ：当current_sum ≥ target时，说明当前窗口满足条件，此时尝试收缩左边界以找到更小的窗口：
    • 更新min_len为当前窗口长度（right - left + 1）和原有min_len的较小值。
    • 将nums[left]从current_sum中减去，然后左指针left右移。
  4. 结果处理 ：若min_len仍为无穷大，说明没有满足条件的子数组，返回 0；否则返回min_len。
三、滑动窗口的适用场景
  • 处理数组 / 字符串的子数组 / 子串问题，尤其是需要优化时间复杂度的场景。
  • 要求子数组 / 子串满足某种条件（如和、长度、字符种类等），并需要求最值（最小长度、最大和等）。
java 复制代码 
package SlidingWindow.SlidingWindow_009;

public class _009 {
    public static void main(String[] args) {
        int[] nums = {2, 3, 1, 2, 4, 3};
        int target = 7;
        Solution solution = new Solution();
        System.out.println(solution.slidingWindow(nums, target)); 
    }
}

class Solution {
    public int slidingWindow(int[] nums, int target) {
        int sum = 0;
        int left = 0;
        int minLength = Integer.MAX_VALUE;

        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];

            while (sum >= target) {
                minLength = Math.min(minLength, right - left + 1);
                sum -= nums[left];
                left++;
            }
        }

        return minLength == Integer.MAX_VALUE ? 0 : minLength;
    }
}

010：3. 无重复字符的最长子串 - 力扣（LeetCode）

暴力解法：

算法思路

枚举「从每一个位置」开始往后，无重复字符的子串可以到达什么位置。找出其中长度最大的即可。

在往后寻找无重复子串能到达的位置时，可以利用「哈希表」统计出字符出现的频次，来判断时候子串出现了重复元素。

java 复制代码 
for (int i = 0; i < n; i++) {
    int[] hash = new int[128];
    int j;
    for (j = i; j < n; j++) {
        char c = s.charAt(j);
        hash[c]++;
        if (hash[c] > 1) {
            break;
        }
    }
    // 跳出后更新：此时j是第一个重复的位置，子串长度是j-i
    ret = Math.max(ret, j - i);
}

方法一：使用HashSet（滑动窗口）

java 复制代码 
import java.util.HashSet;

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s == null || s.length() == 0) return 0;
        
        HashSet<Character> set = new HashSet<>();
        int left = 0, maxLength = 0;
        
        for (int right = 0; right < s.length(); right++) {
            // 如果当前字符已存在，移动左指针直到删除重复字符
            while (set.contains(s.charAt(right))) {
                set.remove(s.charAt(left));
                left++;
            }
            // 添加当前字符到集合
            set.add(s.charAt(right));
            // 更新最大长度
            maxLength = Math.max(maxLength, right - left + 1);
        }
        
        return maxLength;
    }
}

核心区别

1. 存储内容不同

  • HashSet方法：存储当前窗口内的字符

  • HashMap方法 ：存储所有字符最后出现的位置，不管是否在当前窗口内

2. 去重逻辑不同

  • HashSet方法：遇到重复时，从左边界开始逐个删除字符，直到删除重复字符

  • HashMap方法：遇到重复时，通过比较最后出现的位置与左边界，直接跳转到合适的位置

方法二：使用HashMap（优化版）

注意事项1：

put() 方法

这是HashMap中最核心的添加键值对的方法，在代码中用于存储字符和其最新索引。

1. 方法作用
  • 如果键（字符）不存在 ：向map中新增 一个键值对（字符:索引）；
  • 如果键（字符）已存在 ：用新的值（当前索引）覆盖原有值（旧索引），这也是代码中 "保留字符最新索引" 的关键。

注意事项二

left = map.get(currentChar) + 1，算法会在某些场景下出错。下面我们用具体例子和逻辑拆解来说明：

一、核心原因：map中存储的是字符所有历史索引（包括窗口外的旧索引）

哈希表map中存储的是字符最后一次出现的索引 ，但这个索引可能已经在当前窗口的左侧（即 < left） ，属于失效的旧索引 。此时map.get(currentChar) + 1会小于当前的left，如果直接赋值，会导致左指针往回走，窗口中重新包含重复字符。

所以使用max进行一下比较

注意事项三：

一、先理解map.get(currentChar)的含义

map.get(currentChar)返回的是当前字符currentChar上一次出现的索引 （比如字符a上一次出现在索引3，这个方法就返回3）。

二、为什么必须+1？

假设当前字符currentChar上一次出现的索引是idx，如果左指针只移到idx，那么窗口[idx, right]中依然包含两个currentChar（索引idx和right），还是重复的。只有把左指针移到idx + 1，才能彻底排除这个重复的旧字符。

注意事项四：

map.get(currentChar)+1中的map.get(currentChar)，取的是当前字符 "上一次出现的旧索引"（还没被本次的right覆盖），这个旧索引正是导致重复的位置，而+1是为了跳到这个旧索引的下一位，避免重复。

java 复制代码 
import java.util.HashMap;

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s == null || s.length() == 0) return 0;
        
        HashMap<Character, Integer> map = new HashMap<>();
        int left = 0, maxLength = 0;
        
        for (int right = 0; right < s.length(); right++) {
            char currentChar = s.charAt(right);
            
            // 如果字符已存在，移动左指针
            if (map.containsKey(currentChar)) {
                // 确保左指针不会回退
                left = Math.max(left, map.get(currentChar) + 1);
            }
            
            // 更新字符的最新位置
            map.put(currentChar, right);
            // 更新最大长度
            maxLength = Math.max(maxLength, right - left + 1);
        }
        
        return maxLength;
    }
}

方法三：使用数组（最高效）

java 复制代码 
class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length();
        int maxLength = 0;
        int[] charIndex = new int[128]; // 假设是ASCII字符集
        
        for (int left = 0, right = 0; right < n; right++) {
            char currentChar = s.charAt(right);
            // 更新左指针，跳过之前的重复字符位置
            left = Math.max(charIndex[currentChar], left);
            // 更新最大长度
            maxLength = Math.max(maxLength, right - left + 1);
            // 存储下一个索引，作为下次遇到该字符时的跳转位置
            charIndex[currentChar] = right + 1;
        }
        
        return maxLength;
    }
}

方法四：数组模拟hash表

一、核心思想：滑动窗口的 "扩张 - 收缩" 机制

滑动窗口是一种双指针技巧，用两个指针left（左边界）和right（右边界）表示一个连续的区间（窗口）。对于本题：

  1. 扩张窗口 ：右指针right不断向右移动，将新字符纳入窗口，探索更大的子串；
  2. 收缩窗口 ：如果新纳入的字符导致窗口内出现重复，就不断向右移动左指针left，直到窗口内重新无重复；
  3. 记录最大值：每次窗口调整后（无论是扩张还是收缩），计算当前窗口的长度，更新最长无重复子串的长度。

这种机制保证了每个字符最多被left和right各访问一次，因此时间复杂度是 O (n)（n 为字符串长度），远优于暴力枚举的 O (n²)。

二、辅助工具：数组模拟哈希表

要判断窗口内是否有重复字符，需要快速统计字符的出现频次，这里用 ** 长度为 128 的数组hash** 模拟哈希表（替代HashMap），原因如下：

  1. ASCII 字符覆盖：所有可见 / 不可见的 ASCII 字符的编码范围是 0~127，因此数组的索引可以直接对应字符的 ASCII 码；
  2. 高效访问 ：数组的索引访问是 O (1) 时间复杂度，比HashMap的键值对访问更快，且无需处理自动装箱 / 拆箱的开销；
  3. 频次统计 ：hash[字符的ASCII码]的值表示该字符在当前窗口内的出现频次，初始值为 0。
三、具体执行步骤（思路落地）

结合代码的执行流程，把思路拆成 4 个关键步骤：

步骤 1：初始化变量
  • 将字符串转为字符数组s（方便通过索引快速访问字符）；
  • 初始化hash数组（统计字符频次）、left=0（窗口左边界）、right=0（窗口右边界）、ret=0（记录最长长度）。
步骤 2：扩张右边界，纳入新字符

right从 0 开始遍历字符串，每次将s[right]纳入窗口，执行hash[s[right]]++（频次 + 1）。

步骤 3：收缩左边界，消除重复

如果hash[s[right]] > 1（说明当前字符在窗口内重复了），则不断执行：

  • hash[s[left]]--（左边界字符移出窗口，频次 - 1）；
  • left++（左边界右移）；直到hash[s[right]] == 1（窗口内无重复）。

注意 ：这里用while循环而非if判断，因为可能需要多次左移才能消除重复（比如s = "abba"，右边界到第二个a时，需要左移两次才能消除重复的b）。

步骤 4：更新最长长度，继续扩张

计算当前窗口的长度right - left + 1（窗口是闭区间[left, right]），用Math.max(ret, 窗口长度)更新最长长度，然后right++继续探索下一个字符。

四、思路的核心优势
  1. 时间效率高 ：每个字符仅被left和right各遍历一次，时间复杂度 O (n)；
  2. 空间效率高：用固定长度的数组（128 个元素）代替哈希表，空间复杂度 O (1)（与输入字符串长度无关）；
  3. 逻辑简洁：通过窗口的扩张和收缩，将 "找无重复子串" 的问题转化为 "维护窗口有效性" 的问题，降低问题复杂度。
java 复制代码 
class Solution
{
    public int lengthOfLongestSubstring(String ss)
    {
        char[] s = ss.toCharArray();
        
        int[] hash = new int[128]; // 用数组模拟哈希表
        int left = 0, right = 0, n = ss.length();
        int ret = 0;
        while(right < n)
        {
            hash[s[right]]++; // 进入窗口
            while(hash[s[right]] > 1) // 判断
                hash[s[left++]]--; // 出窗口
            ret = Math.max(ret, right - left + 1); // 更新结果
            right++; // 让下一个字符进入窗口
        }
        return ret;
    }
}

算法详解

核心思想：滑动窗口

使用两个指针（left 和 right）表示当前不重复子串的窗口：

  • left：窗口左边界

  • right：窗口右边界

三种数据结构的对比

  1. HashSet

    • 优点：实现简单，易于理解

    • 缺点：遇到重复字符时，左指针需要逐步移动

  2. HashMap

    • 优点：O(1)时间复杂度查找字符位置

    • 优点：可以直接跳转到重复字符的下一个位置

    • 缺点：需要额外存储字符索引

  3. 数组

    • 优点：最快，O(1)时间复杂度

    • 优点：内存占用固定（128字节）

    • 限制：仅适用于ASCII字符

时间复杂度与空间复杂度

  • 时间复杂度：O(n)，其中 n 是字符串长度

  • 空间复杂度：O(min(m, n))，其中 m 是字符集大小

相关推荐
!停2 小时前
字符函数和字符串函数
算法
AI科技星2 小时前
圆柱螺旋运动方程的一步步求导与实验数据验证
开发语言·数据结构·经验分享·线性代数·算法·数学建模
FONE_Platform2 小时前
FONE食品饮料行业全面预算解决方案：构建韧性增长
人工智能·算法·全面预算·全面预算管理系统·企业全面预算
月明长歌2 小时前
【码道初阶】【Leetcode94&144&145】二叉树的前中后序遍历（非递归版）：显式调用栈的优雅实现
java·数据结构·windows·算法·leetcode·二叉树
DanyHope3 小时前
《LeetCode 49. 字母异位词分组：哈希表 + 排序 全解析》
算法·leetcode·哈希算法·散列表
iAkuya3 小时前
(leetcode) 力扣100 15轮转数组（环状替代）
数据结构·算法·leetcode
杰克尼3 小时前
蓝桥云课-5. 花灯调整【算法赛】
java·开发语言·算法
.小墨迹3 小时前
C++学习之std::move 的用法与优缺点分析
linux·开发语言·c++·学习·算法·ubuntu
wanghowie3 小时前
01.02 Java基础篇｜核心数据结构速查
java·开发语言·数据结构
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04sqli-labs靶场通关笔记：第18-19关 HTTP头部注入05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07BongoCat - 跨平台键盘猫动画工具08RedissonClient的配置解析09jdk21下载、安装（Windows、Linux、macOS）10Labelme从安装到标注：零基础完整指南