Sentaurus Workbench10. 优化框架
10.1 入门 10.2 基础优化 10.3 示例:沟槽栅极 NMOS 导通电阻优化
目标
- 介绍 Sentaurus Workbench 优化框架。
- 演示如何使用优化框架的不同功能。
10.1 入门
优化框架是一种旨在高效提取 TCAD 仿真通用信息的工具。例如,它可用于确定满足给定设计规格的参数集,或分析参数变化如何影响器件行为。
优化框架可用于多种用途。它提供以下功能:
- 优化 (Optimization):允许您为给定的目标规格找到最优的参数集。多个优化目标可以组合在一起,并通过权重指定其相对重要性。提供多种算法来解决优化问题。
- 筛选分析 (Screening analysis):展示不同参数对仿真响应的影响,帮助您确定最相关的参数。
- 敏感性分析 (Sensitivity analysis):确定对给定参数的微小变化如何影响仿真响应。
- 响应面建模 (Response surface modeling):将预定义的模型拟合到数据,可用于更好地理解趋势(用于插值、近似感兴趣的物理量等)。
优化框架提供了一个 Python 环境,允许您定义和使用自定义算法来解决特定任务。优化框架的各个组件可以组合起来制定优化策略。例如,可以将筛选分析与优化相结合:通过筛选分析找到重要的目标参数,然后仅对这些参数进行优化。
优化框架与 Sentaurus Workbench 的批处理工具交互,用于设置和运行仿真(Sentaurus Workbench 实验)。
本节涵盖以下主题:
- 章节 10.1.1 访问优化框架
- 章节 10.1.2 优化框架输入文件
- 章节 10.1.3 运行优化
- 章节 10.1.4 重新启动优化
- 章节 10.1.5 重置项目
- 章节 10.1.6 优化框架输出日志
10.1.1 访问优化框架
在访问优化框架之前,必须通过高级模式启动 Sentaurus Workbench:
bash
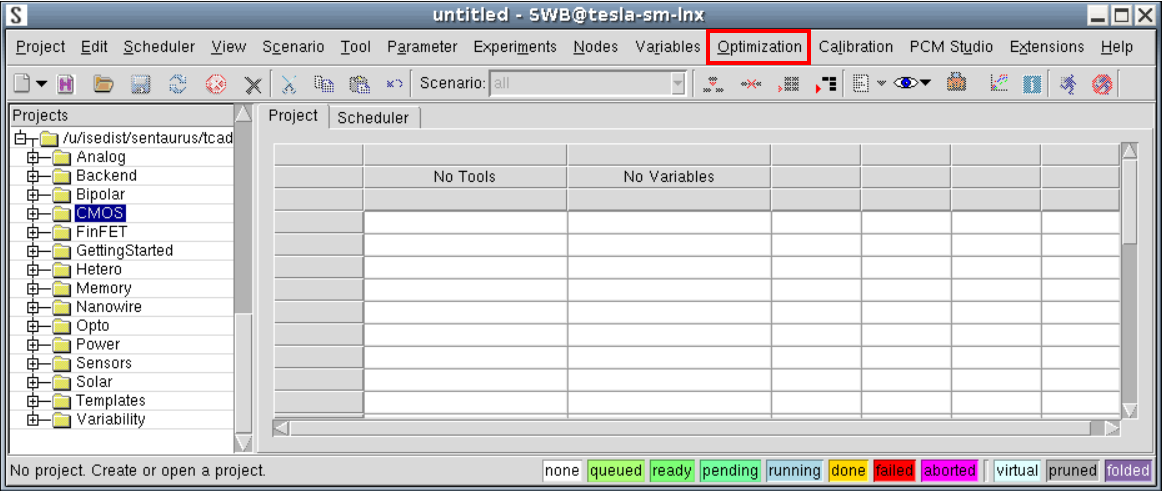
swb -a &此时菜单栏将显示 Optimization(优化)菜单(见图1)。
优化菜单
图1. 高级模式下 Sentaurus Workbench 主窗口(优化菜单已高亮显示)。(单击图像查看完整视图。)
10.1.2 优化框架输入文件
可通过 Sentaurus Workbench 菜单栏访问优化框架输入文件 genopt.py:选择 Optimization > Edit Python Input(见图2)。
图2. Sentaurus Workbench 中的优化菜单。
优化项目输入文件 genopt.py 通常包含四个部分:优化参数定义、优化目标与约束定义、目标优化策略,以及可选的实验结果后处理。
好的,这是您提供文本的中文翻译,尽可能保留了原意:
10.1.3 运行优化
优化设置完成后,您可以运行优化框架 (Optimization Framework)。要从 Sentaurus Workbench 的图形用户界面运行优化框架,请选择 优化 > 运行(参见图 2)。
或者,在命令行中输入:
genopt [options] [project_dir]
其中 [project_dir] 是要执行的 Sentaurus Workbench 项目的路径。优化框架 (genopt) 将使用 [project_dir] 目录下的 Python 脚本 genopt.py 作为输入文件。
有关可用的命令行选项,请参阅《Sentaurus™ Workbench 优化框架用户指南》。
10.1.4 重启优化
有时需要从先前执行过的优化项目重新启动优化。这可能是因为之前的执行失败,或者您希望在重用所有已完成仿真的同时更改输入文件。
优化框架使用场景 (scenarios) 来定义项目可以重新启动的条件。可用于重启的场景是 initial 和 restart_*(例如,restart_1 或 restart_2)。restart_* 场景会自动创建,其中包含每个阶段的最优参数值。
要从 Sentaurus Workbench 的图形用户界面重启优化框架,请选择 优化 > 从 > <场景> 重启 (参见图 3)。除非项目中存在有效的重启场景,否则 从...重启 命令不可用。
Figure 3. Menu showing command for restarting scenario
如果从 initial 场景重启且未更改输入文件,则将执行相同的优化,并重用所有先前已完成的实验。当优化因外部原因(例如计算集群中的网络故障)失败时,这通常是所需的行为。唯一的例外是输入文件中存在用于随机数生成器的随机种子选择:
python
np.random.seed()在这种情况下,一旦使用了新的随机数,新的优化将与之前的优化产生差异。
当使用 restart_* 场景之一时,该场景将被视为此次运行的初始场景。例如,当使用命令:
python
optimizer.set_from_swb(params)时,参数值将被设置为该场景中的值。与之前一样,任何已执行的实验都将被重用。
10.1.5 重置项目 (Resetting the Project) 要移除由优化框架生成的所有实验,请选择 优化 (Optimization) > 重置项目 (Reset Project) (参见图 2)。此命令将仅保留属于 initial(初始)场景的实验,并删除所有其他实验及其输出。属于 initial(初始)场景的节点不会被清理。
10.1.6 优化框架输出日志 (Optimization Framework Output Log) 启动优化框架的执行后,会打开一个带有输出日志的对话框。关闭对话框后,您可以通过选择 优化 (Optimization) > 查看日志 (View Log)(参见图 2)重新打开它。
使用默认的详细程度 (verbosity) 设置时,输出日志会显示有关已执行实验的信息,这些信息有助于跟踪优化的进度。
图 4 显示了输出日志的一个典型部分。每次调用优化器方法(如 optimize()、search() 和 sensitivity_analysis())被称为一个阶段 (stage),在其执行开始时会打印一个标题(参见图 4 中的绿色框)。
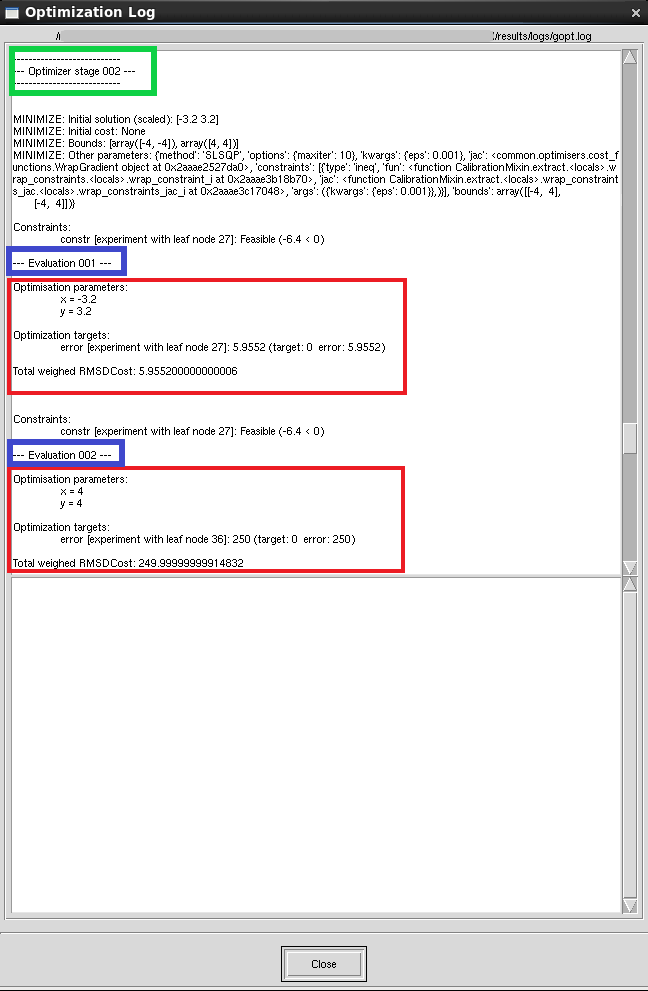
当一个实验完成后,会打印评估编号(该编号在每个阶段开始时重置为 1;参见图 4 中的蓝色框),后跟参数值、输出值和总误差(参见图 4 中的红色框)。
输出值包括从中提取它们的 Sentaurus Workbench 实验(数字对应于实验的最后一个节点编号)、为其设置的目标以及误差贡献。
10.2 基础优化
本节通过一个使用解析函数的简单示例,解释如何设置一个优化项目及其主要组成部分。
这里使用的项目可以在 Applications_Library 目录中找到。图 5 显示了项目在优化前的初始状态。
优化前的项目
图 5. 运行优化框架之前的 Sentaurus Workbench 项目。(点击图片查看完整视图。)
通常,一个优化项目可以包含任何 TCAD 工艺和器件仿真,就像 Sentaurus Workbench 通常所做的那样。在这个简单的例子中,它只包含一个 Python 工具,其输入如下:
python
x = @x@
y = @y@
value = (x**2+y-11)**2 + (x+y**2-7)**2
constraint = x - y
print(f"DOE: error {value}")
print(f"DOE: constr {constraint}")该工具的输入是两个 Sentaurus Workbench 参数 x 和 y,它们在前两行中使用预处理命令 @x@ 和 @y@ 引用。优化框架依赖 Sentaurus Workbench 参数来定义输入空间,因此,需要使用待优化参数的工具必须像本例一样通过预处理指令来获取它们的值。
作为输出,该工具计算了一个解析函数的值 (value) 和一个将用于定义约束 x < y 的函数的值 (constr),参见图 6。为了让优化框架能够使用这些值,它们必须被写成 Sentaurus Workbench 变量,这是通过 print 命令实现的。
用于优化的测试函数
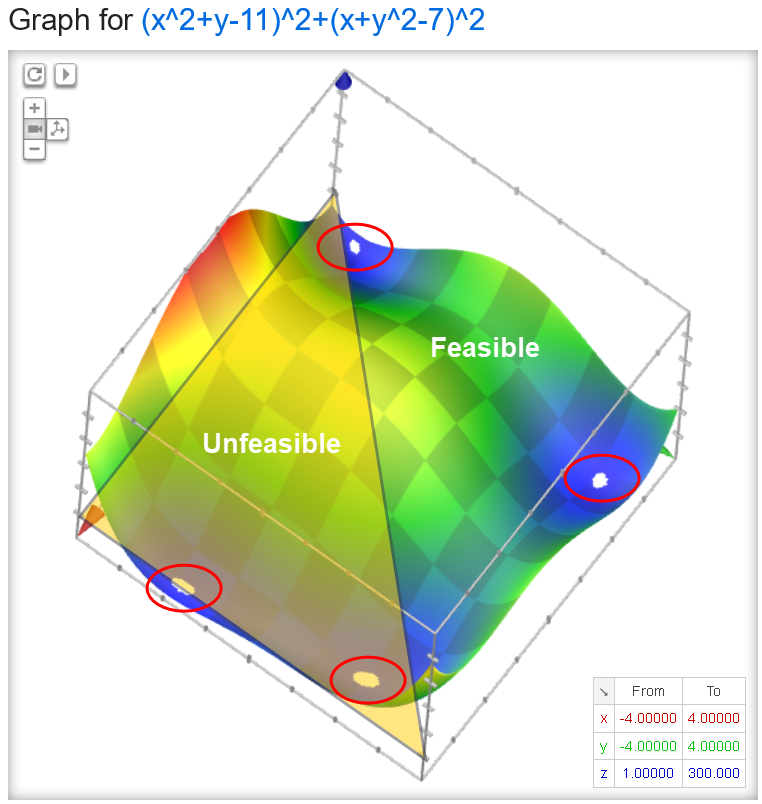
图 6. 用于优化的测试函数。(点击图片查看完整视图。)
输入文件(选择 Optimization > Edit Python Input)定义了一个可能由多个任务组成的优化策略。这个文件是一个 Python 脚本,其中注入了与优化框架相关的一些附加类和对象,包括:
optimizer:这是优化框架的主要对象。在内部,它驱动优化过程并管理 Sentaurus Workbench 项目。优化任务通过调用此对象的方法来执行。OptParam和TOptParam:这些是表示优化参数的类。它们管理参数值、边界和变换 (TOptParam)。OptTarget:这是一个表示优化过程目标的类。通常,它需要响应(仿真输出,可能经过后处理)和该仿真输出的目标值。您可以指定额外的属性,例如权重。
图 4. 优化框架输出日志。(点击图片查看完整尺寸视图。)
10.2.1 优化参数
项目输入文件的第一部分是优化参数的定义:
python
x = TOptParam('x', 0, -4, 4)
y = TOptParam('y', 0, -4, 4)
params = [x, y]
optimizer.set_from_swb(params)前两行使用 TOptParam 类定义参数。第一个参数('x' 和 'y')是要优化的 Sentaurus Workbench 参数名称,第二个参数是初始值,后接参数的上下界。这些参数被组合到列表 params 中以便后续使用。最后,通过优化器对象的 set_from_swb 方法将参数值设置为项目中当前分配的值。本例中数值相同,但通常此命令可确保输入文件与项目的一致性。
10.2.2 优化目标
优化目标用于定义需要优化的量值,与约束条件共同构成优化问题的输出空间。
在优化框架中,目标和约束基于 Sentaurus Workbench 项目变量定义,这些变量通常由仿真工具或后处理阶段写入。本示例的目标定义为:
python
# 定义优化目标
t1 = OptTarget("error", value=0, scale=1)
targets = [t1]这些命令定义了一个优化目标,将尝试使输出变量 error 匹配目标值 0。
如前所述,此示例输出存在四个最小值。当已知最优解需满足特定附加条件时,可添加约束。本例添加约束以获取 x\
python
# 定义约束 (x-y<0)
c1 = OptConstraint("constr", lt=0)
constraints = [c1]其中 lt 表示小于(less than)。如前所述,输出变量 constr 包含 x-y 的值,因此施加的约束为 constr \< 0。
10.2.3 优化策略
定义参数和目标后,优化的核心第三部分是定义策略,即如何结合参数和目标以达到最优解。
示例包含两部分:全局搜索和局部最小化。由于待最小化函数非凸,将在使用局部最小化算法寻找最小值前尝试寻找良好起点。
好的,这是您提供文本的中文翻译,尽可能保留了原意:
对 optimizer.search 的调用会在一系列点执行问题并返回最佳值。例如:
参数搜索 - 网格 (Grid)
python
opt_params = optimizer.search(params, targets + constraints,
method="grid", options={"Ns": 5}
)在此示例中,method="grid" 表示要执行的点在 params 定义的输入空间中构成一个网格,而选项 "Ns": 5 表示这应该是一个 5x5 的网格。对于这 25 个实验中的每一个,目标和约束都将被评估,该调用将返回在满足约束条件下产生最低目标值的参数值。
10.2.3.2 局部优化 (Local Optimization) 该示例使用一个局部优化器来精炼搜索找到的值。局部优化的选项通过后端 (backend) 设置,可以使用 optimizer.backend 访问。例如:
局部优化 (Local Minimization)
python
optimizer.backend.set_method("minimize")
optimizer.backend.set_optimization_parameters(jacobian_options={"eps": 1e-3},
method="SLSQP",
options={"maxiter": 10})在此示例中,您选择了后端 minimize,它提供了访问通用优化算法的途径。选择的算法是 SLSQP,这是一种基于梯度的优化算法,支持一般的非线性约束。最后,为了限制创建的实验数量,选项 maxiter 被设置为 10。
设置好后端的选项后,您可以运行局部优化,例如:
python
opt_params = optimizer.optimize(params, targets + constraints)与之前一样,对 optimizer.optimize 的调用需要参数、目标和约束。
10.2.4 优化之后 随着优化的进行,Sentaurus Workbench 项目会更新和刷新,因此仿真工具产生的所有中间结果都是可用的。图 7 显示了优化完成后项目的状态。
运行优化框架后的 Sentaurus Workbench 项目
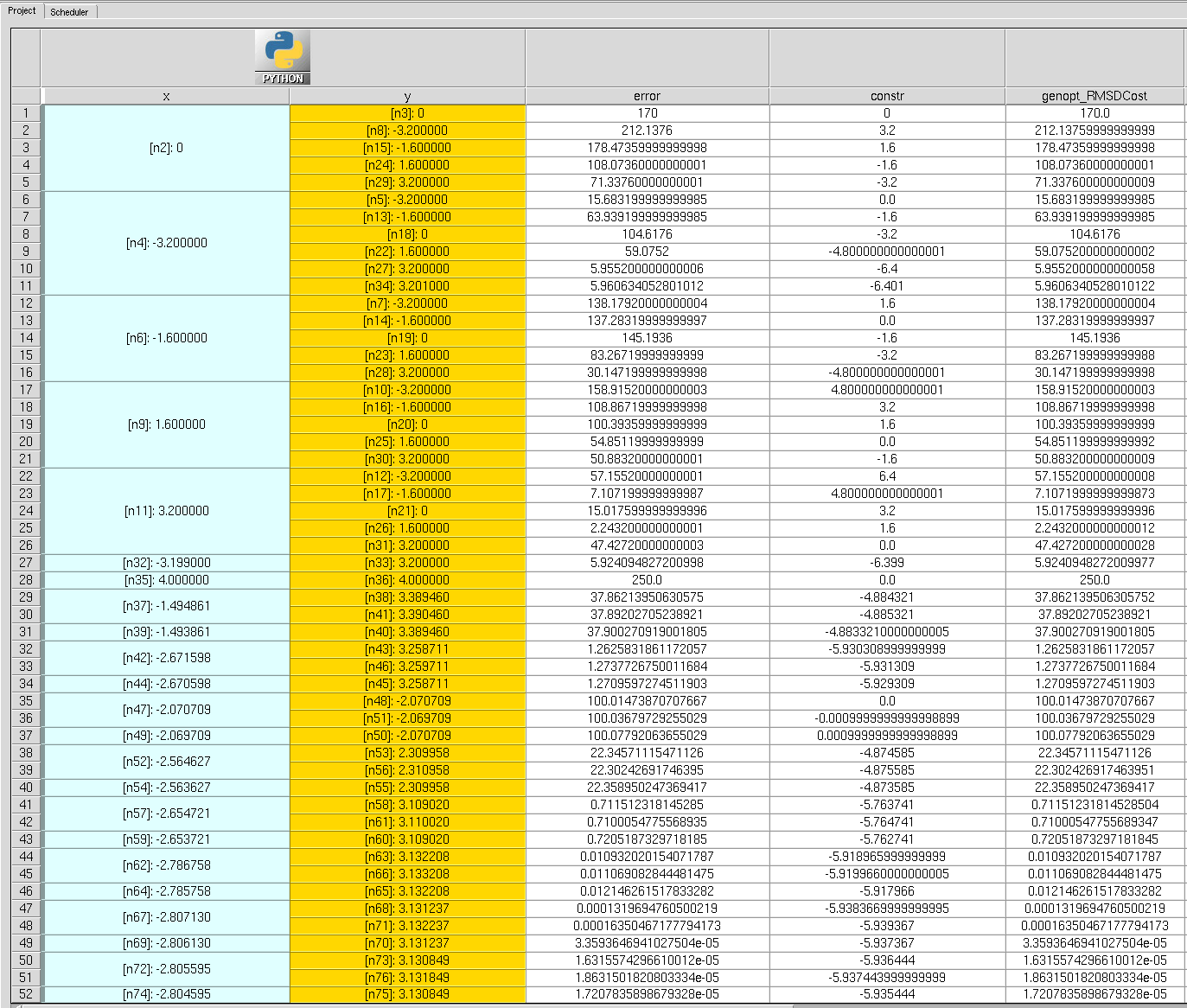
图 7. 运行优化框架后的 Sentaurus Workbench 项目。(点击图片查看完整尺寸视图。)
为了简化优化器项目的可视化,所有实验都被添加进额外的场景中。图 8 显示了优化完成后的场景列表。
为了简化优化器项目的可视化,所有实验都被添加到附加场景中。图8展示了优化后的场景列表。
运行优化框架后的场景
图8. 运行优化框架后的场景
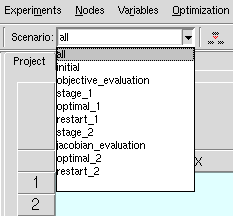
创建的场景包含以下实验:
- objective_evaluation:主优化轨迹中的实验
- jacobian_evaluation:用于评估数值逼近雅可比矩阵的实验(该矩阵用于驱动基于梯度的优化)
- initial:初始项目中的实验
- optimal_1, optimal_2:分别包含在调用 optimizer.search() 和 optimizer.optimize() 之后使用最优参数集执行的实验
- restart_1, restart_2:包含 initial 场景的副本,其中优化参数已分别替换为 optimizer.search() 和 optimizer.optimize() 调用之后的最优参数
- stage_1, stage_2:分别包含在 optimizer.search() 和 optimizer.optimize() 调用期间执行的所有实验(不包括雅可比评估)
10.2.4.1 输出数据
除实验生成的数据外,优化框架产生的部分数据可在优化器节点文件夹的 genopt_plots 和 genopt_data 目录中获取。通过 Sentaurus Workbench 节点浏览器访问数据的操作步骤如图 9 所示。
优化框架输出文件夹
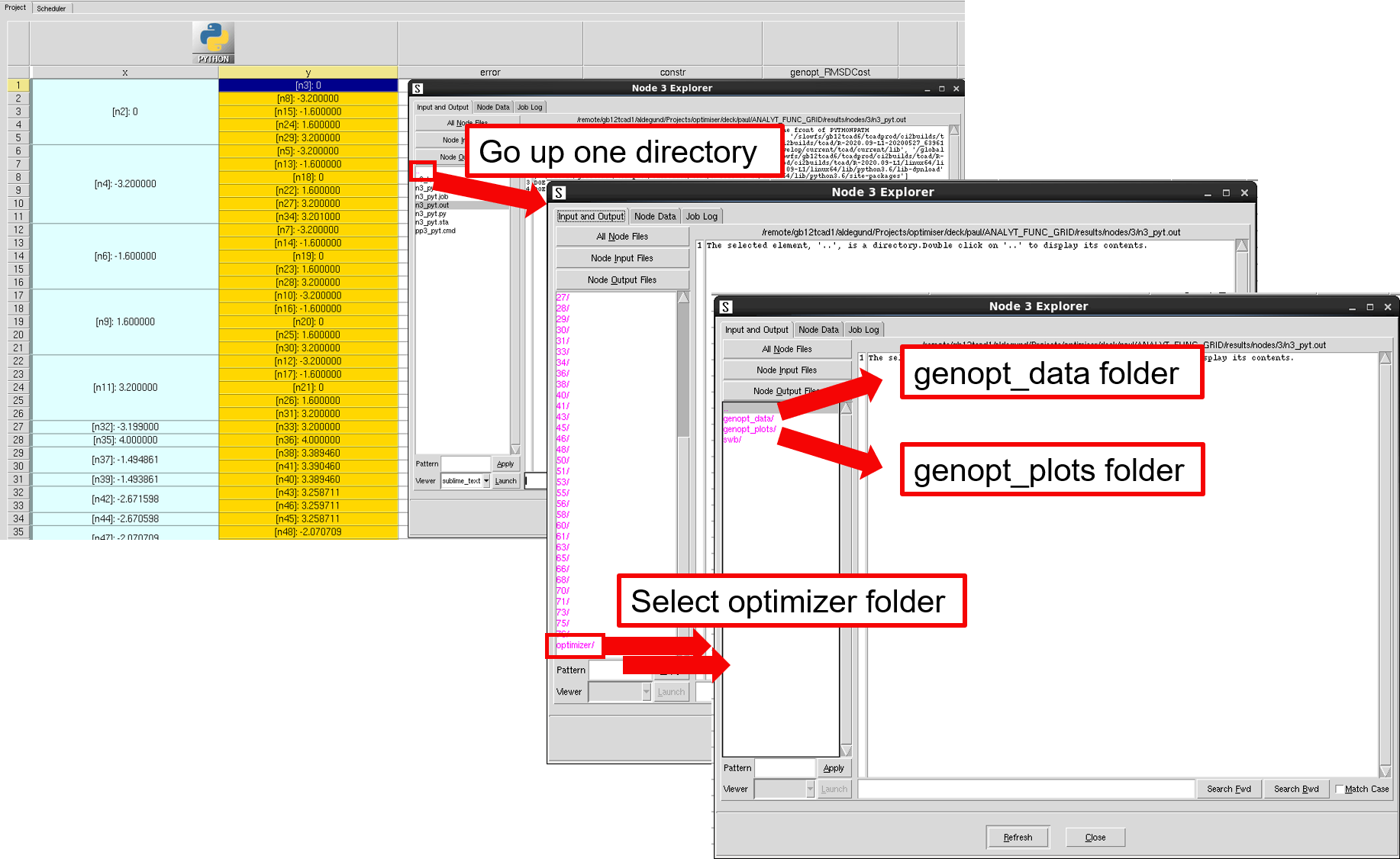
图 9. 优化器输出文件夹路径。(点击图片查看完整尺寸。)
genopt_data 文件夹包含优化各阶段的 CSV 文件,其中记录了输出值、输出误差(与目标值的距离)及总误差,如图 10 所示。注意输出列数据包含在方括号内,若需在绘图应用程序中直接使用该文件,可能需要先移除这些括号。
优化框架 genopt_data 文件夹
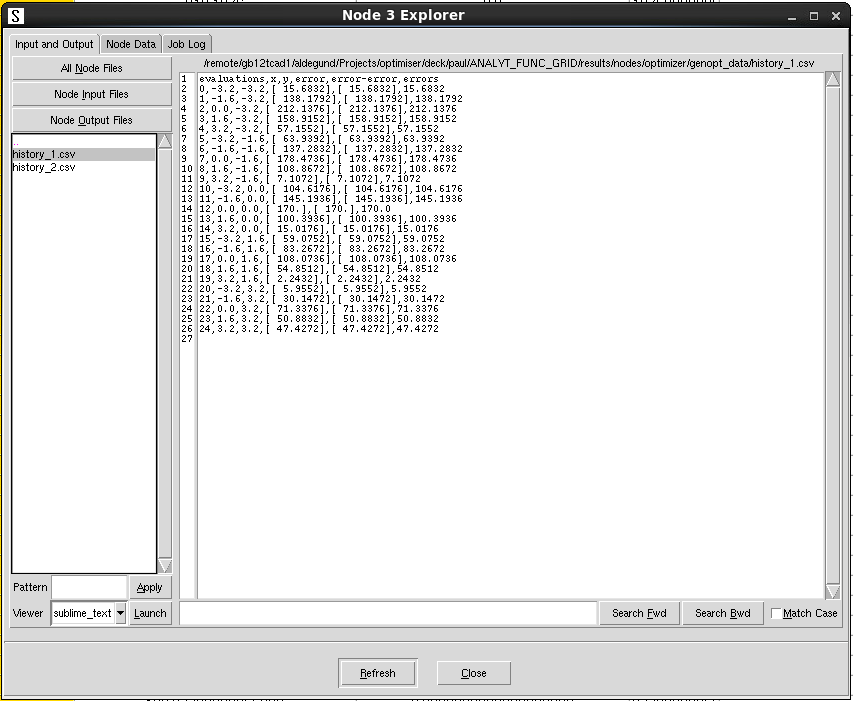
图 10. 运行优化框架后的 genopt_data 文件夹。(点击图片查看完整尺寸。)
genopt_plots 文件夹包含优化框架创建的所有图形,如图 11 所示。此示例中,收敛曲线由 optimizer.optimize 调用生成,但也包含来自 optimizer.search 调用的数据。
运行优化框架后的 genopt_plots 文件夹
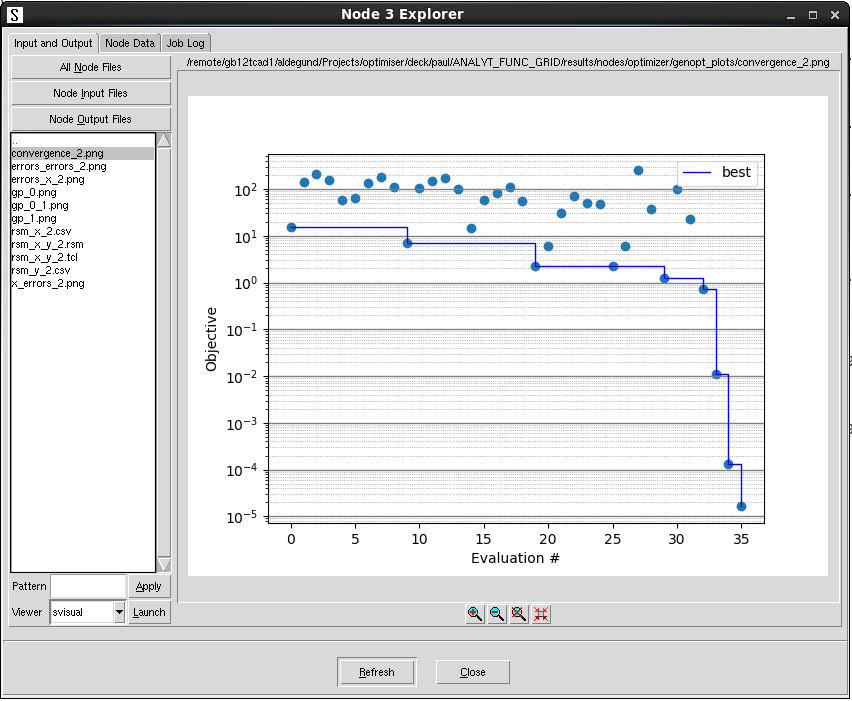
图 11. 运行优化框架后的 genopt_plots 文件夹。(点击图片查看完整尺寸。)
gp_.png 和 rsm_ 文件包含通过 optimizer.search 调用拟合总误差的响应面模型(RSM)一维切面线与二维切面图。图 12 展示了二维 RSM 等高线图,其中黑点表示模拟位置,背景十字标记代表 RSM 的不确定性------蓝色阴影表示较低不确定性,红色阴影表示较高不确定性。
图 12. 二维 RSM 文件。(点击图片查看完整尺寸视图。)
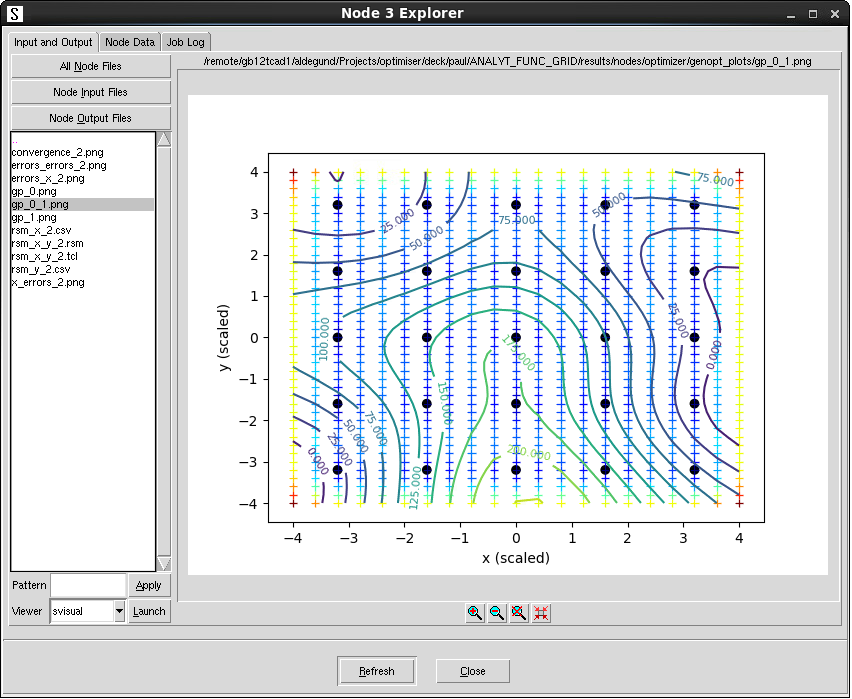
图 13 展示了一条在找到的最佳点处截取的一维切割线。在此图中,圆圈再次代表仿真数据。由于数据是二维的,并非所有点都距离切割线相同。该距离通过圆圈的背景颜色表示:颜色越深,表示距离切割线越近。此图展示了之前在函数图(图 6)中见过的特征性双势阱。蓝线对应于 RSM 的平均预测值,细红线则显示了预测均值周围的 ± 一个标准差范围。
RSM 的一维切割线
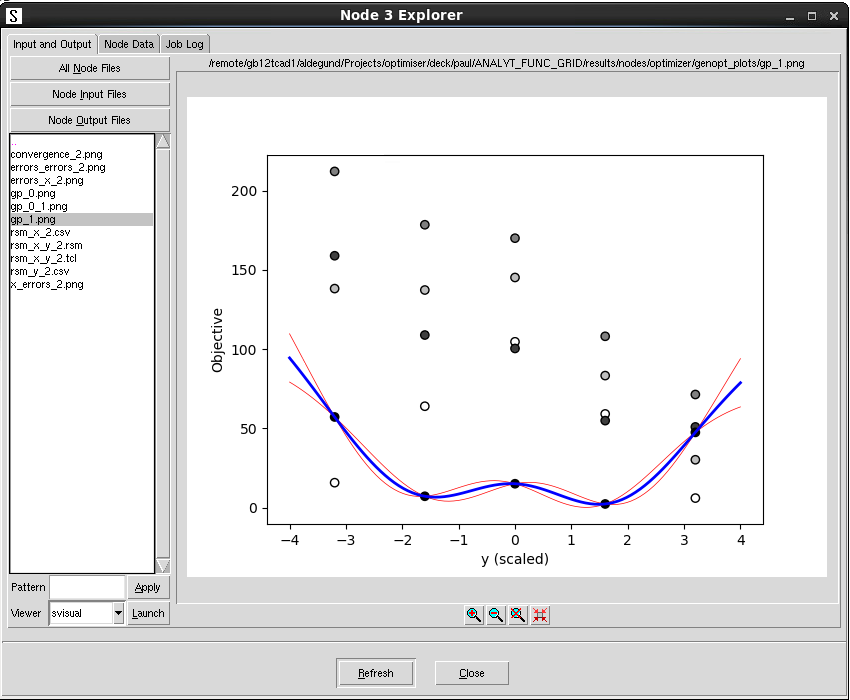
图 13. RSM 的一维切割线。(点击图片查看完整尺寸视图。)
文件 rsm_*.tcl 和 rsm_*.csv 包含了 RSM 数据,其格式可以在 Sentaurus Visual 中打开,如图 14 所示。
在 Sentaurus Visual 中打开的 RSM 文件
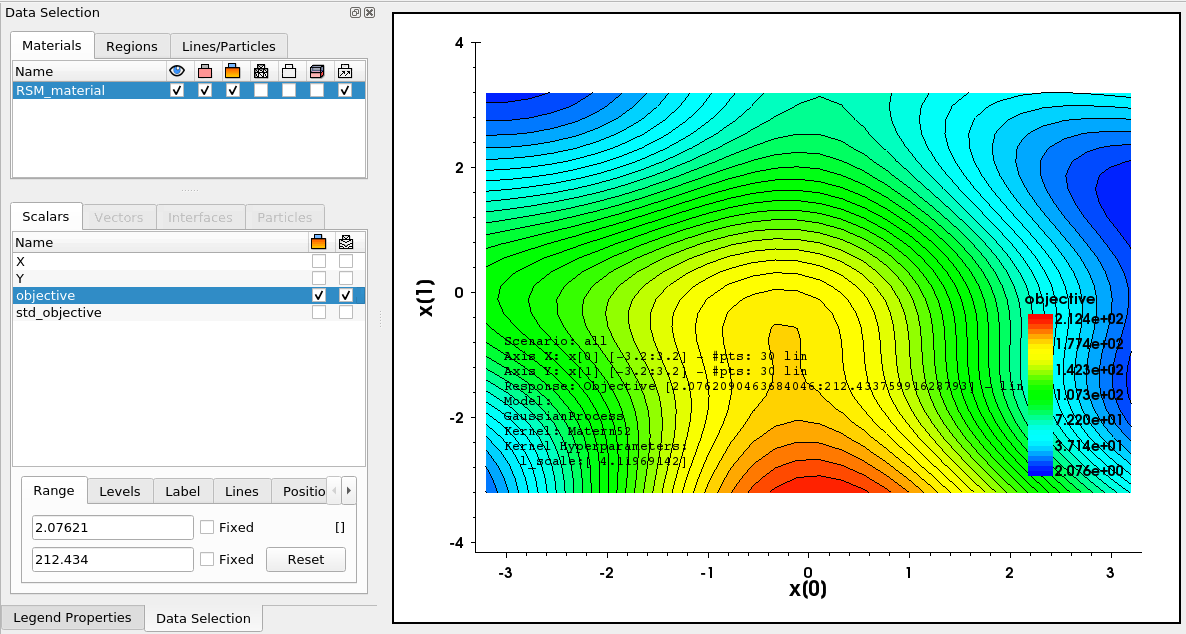
图 14. 在 Sentaurus Visual 中打开的 RSM 文件。(点击图片查看完整尺寸视图。)
10.3 实例详解:沟槽栅 NMOS 导通电阻优化
本节将引导您完成针对沟槽栅 NMOS 器件的工艺条件优化过程,目标是实现低导通电阻,同时确保击穿电压不低于给定值。
10.3.1 沟槽栅 NMOS 结构与项目组织
此处使用的示例是一个沟槽栅 NMOS 器件。其结构如图 15 所示。
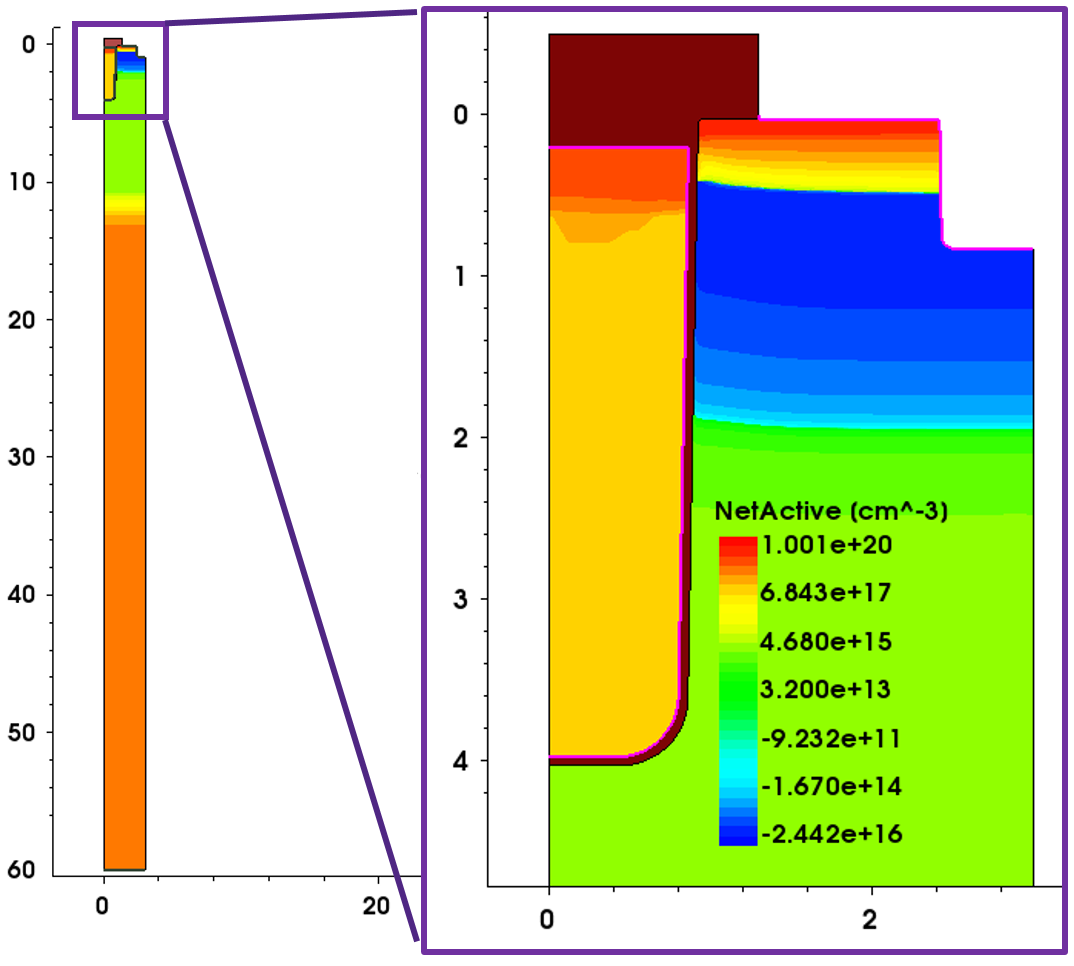
沟槽栅 NMOS 示例结构
图 15. 沟槽栅 NMOS 示例的结构。(点击图片查看完整尺寸视图。)
已设置一个 TCAD 输入文件,用于通过 Sentaurus Device 模拟该沟槽栅 NMOS 器件的 Id--Vg、Id--Vd 以及击穿特性,如图 16 所示。根据 I--V 结果,可以提取阈值电压(Vth)、导通电阻(Ron)和击穿电压(BV)(此处使用 Sentaurus Visual)。
沟槽栅 NMOS 示例的 TCAD 输入文件

图 16. 沟槽栅 NMOS 示例的 TCAD 输入文件。(点击图片查看完整尺寸视图。)
Ron 和 BV 会受到工艺参数的影响,例如 nepi1D 和 pwellD。本示例阐述了如何使用优化框架(Optimization Framework)来优化工艺参数,从而在击穿电压大于 80 V 的条件下,输出具有最小导通电阻的器件。
对于一个优化项目,需要更改的参数必须定义为 Sentaurus Workbench 参数(Sentaurus Workbench parameters),而用于计算目标值的输出必须定义为 Sentaurus Workbench 变量(Sentaurus Workbench variables)。
10.3.2 定义优化参数与目标
与之前的示例类似,输入文件的开头包含了优化参数和目标的定义。
python
# 定义优化参数。名称必须是 Sentaurus Workbench 参数。
a = TOptParam('nepi1D', 1.0e16, 1.0e15, 2.0e16, Log10)
b = TOptParam('pwellD', 1.0e13, 1.0e12, 1.0e14, Log10)
params = [a, b]这段代码定义了两个优化参数,分别对应 Sentaurus Workbench 参数 nepi1D 和 pwellD。此处对这些参数应用了对数变换(Log10),因此优化过程在内部是针对 \\log_{10}(\\text{nepi1D}) 和 \\log_{10}(\\text{pwellD}) 进行的。这对于跨越数量级(orders of magnitude)的参数特别有用。
该问题只有一个目标,即您希望最小化的导通电阻(Ron)。其定义如下:
python
# 定义优化目标
t1 = OptTarget("Ron")
targets = [t1]除了目标之外,您还需要定义一个关于击穿电压的约束条件,该电压被写入 Sentaurus Workbench 变量 BV,要求其大于 80:
python
# 定义优化约束
c1 = OptConstraint("BV", gt=80.0)
constraints = [c1]10.3.3 优化策略 优化策略也在输入文件中定义。在本案例中,它包含两部分:初始搜索和在最佳值附近的局部最小化。
10.3.3.1 初始搜索 首先,使用 Sobol 序列对输入空间进行采样:
参数搜索
python
opt_params = optimizer.search(params, targets + constraints,
method="sobol",
options={ "Ns": 20 }
)这将生成 20 个样本点,均匀分布在经过变换的输入空间中。使用初始搜索有助于更好地理解目标的行为,并为局部最小化选择一个良好的起始点。
图 17 展示了初始采样点以及拟合到数据(忽略约束)的响应面模型 (RSM),以便直观地展示目标随输入参数的变化情况。
初始采样及拟合目标的响应面模型
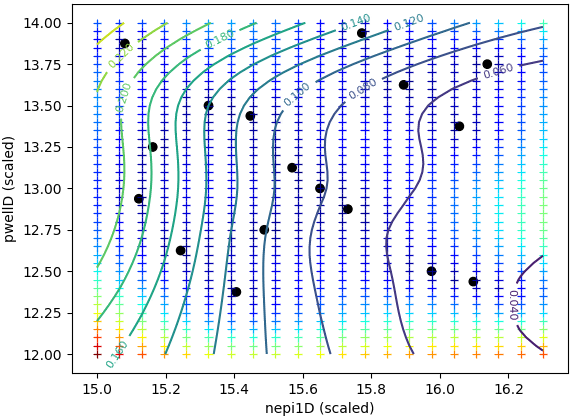
图 17. 初始采样点及忽略约束条件拟合目标的响应面模型。
图 18 展示了在最优解处沿两个维度的一维剖面线。最佳可行解由虚线标出。可以明显看到,对于较大的 nepi1D 值,许多点提供了更低的导通电阻,但它们违反了施加在击穿电压上的约束条件。这一点在图 19 中可以清晰地看到,该图比较了搜索最优解(节点)和节点 54(该节点导通电阻更低但违反约束条件)的击穿特性曲线。
初始采样及拟合目标响应面模型的一维剖面线
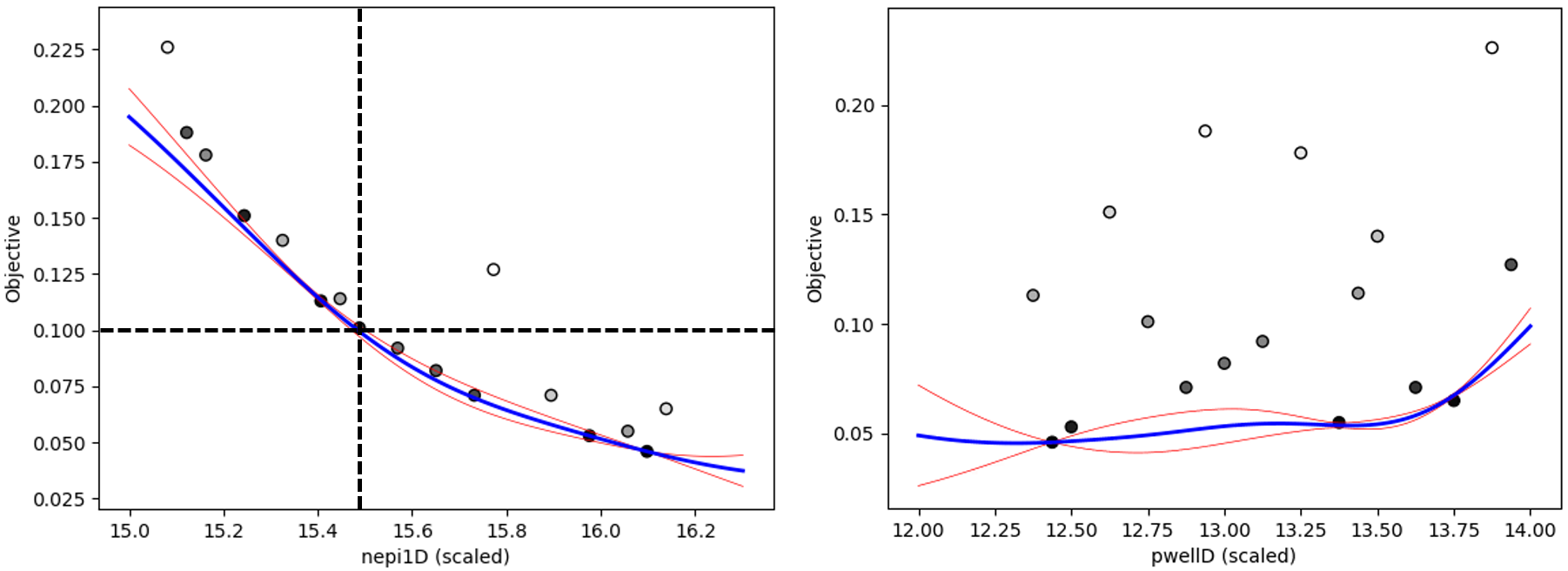
图 18. 初始采样点及忽略约束条件拟合目标响应面模型的一维剖面线。(点击图片查看完整尺寸视图。)
击穿电压曲线图
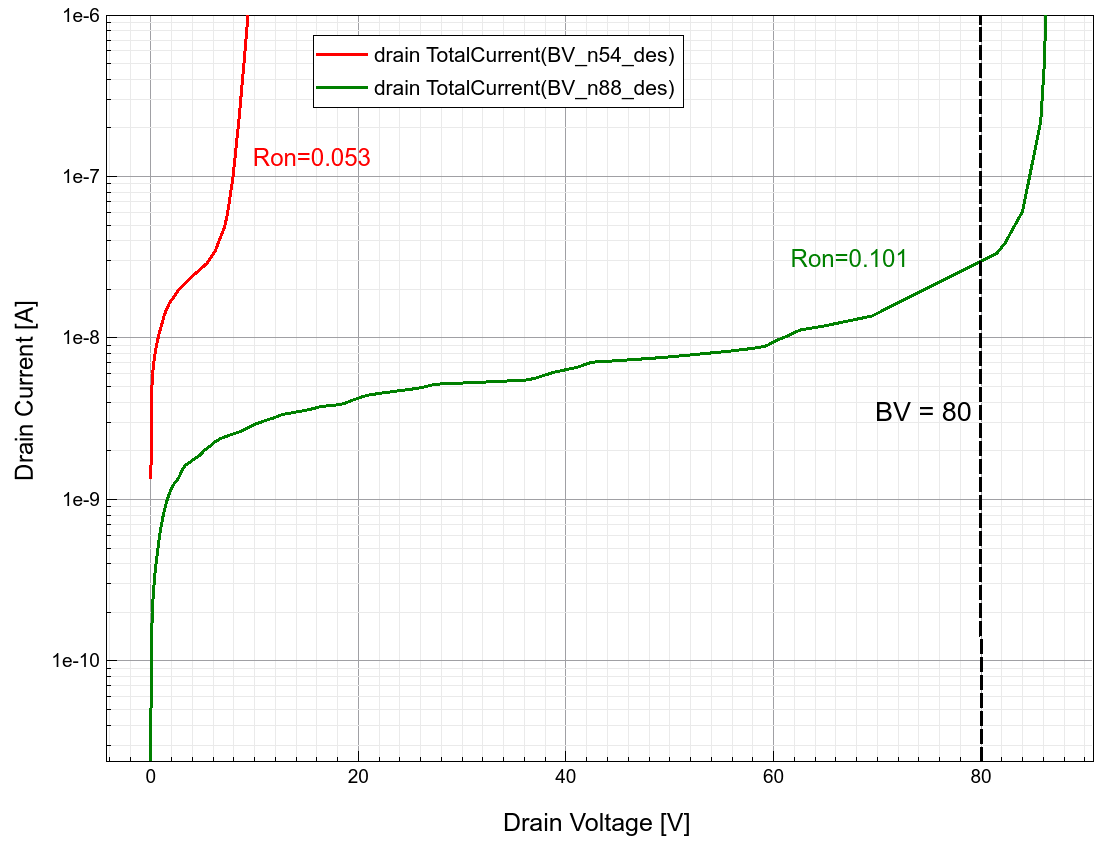
图 19. 搜索过程中具有最低导通电阻的节点 (54) 和满足击穿电压约束条件下具有最低导通电阻的节点 (88) 的击穿电压曲线图。(点击图片查看完整尺寸视图。)
10.3.3.2 局部优化 (Local Optimization)
在完成初始搜索后,您执行局部最小化来优化初始搜索中找到的最佳结果。唯一能够考虑约束条件的基于梯度的方法是 SLSQP,它可以通过 minimize 后端使用:
局部最小化 (Local minimization)
python
optimizer.backend.set_method("minimize")
optimizer.backend.set_optimization_parameters(
jacobian_options={"eps": 1.e-2},
method="SLSQP",
options={"ftol": 1e-4, "maxiter": 10}
)
opt_params = optimizer.optimize(params, targets + constraints)为了限制运行时间,您将算法的最大迭代次数设置为 10,并将目标函数的变化容差设置为 1e-4。
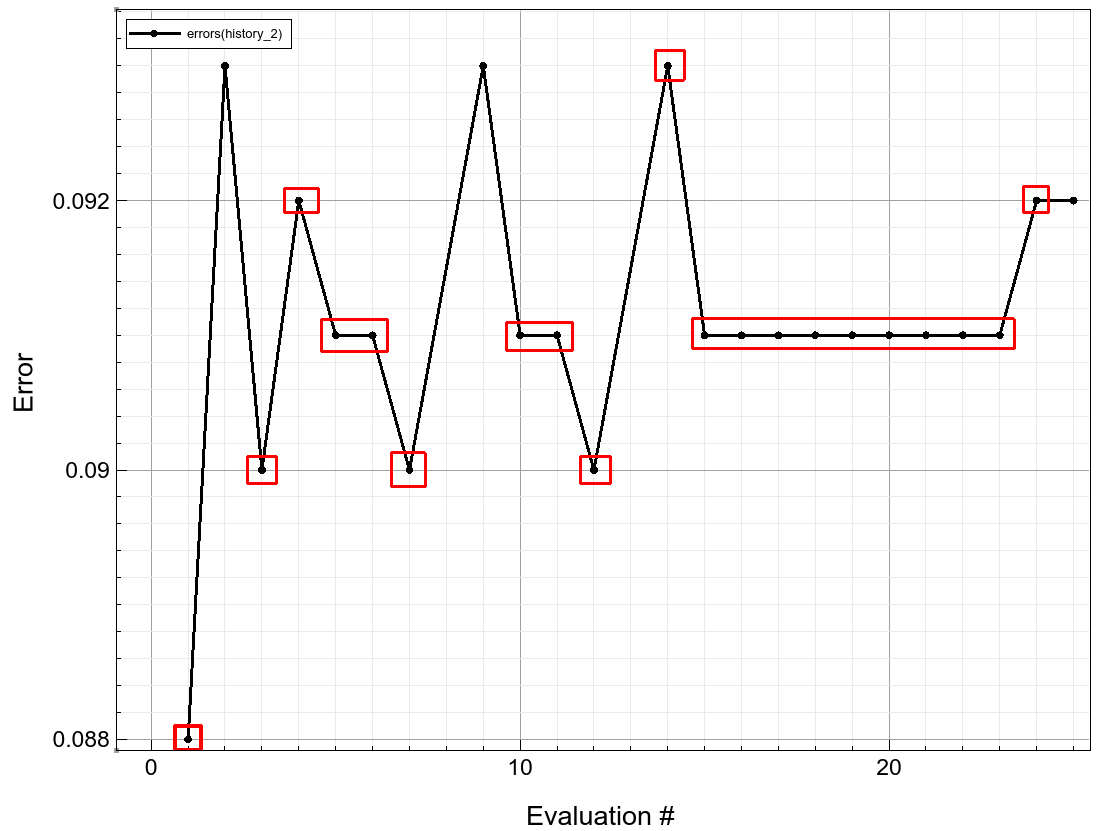
图 20 显示了初始搜索后局部最小化的收敛过程。红色方框表示不可行解。该最小化算法似乎从空间的不可行区域接近局部最小值,在尝试了几个更优但不可行的解之后,找到了一个可行的局部最小值。
初始搜索后局部最小化的收敛过程
图 20. 初始搜索后局部最小化的收敛过程。红色方框表示不可行解。(点击图片查看完整尺寸。)
这与忽略约束条件的局部最小化形成对比,后者如图 21 所示,迅速收敛到一个局部最小值。然而,该局部最小值违反了所需的约束条件,其 BV 值达到了 52 V。
初始搜索后局部最小化的收敛过程
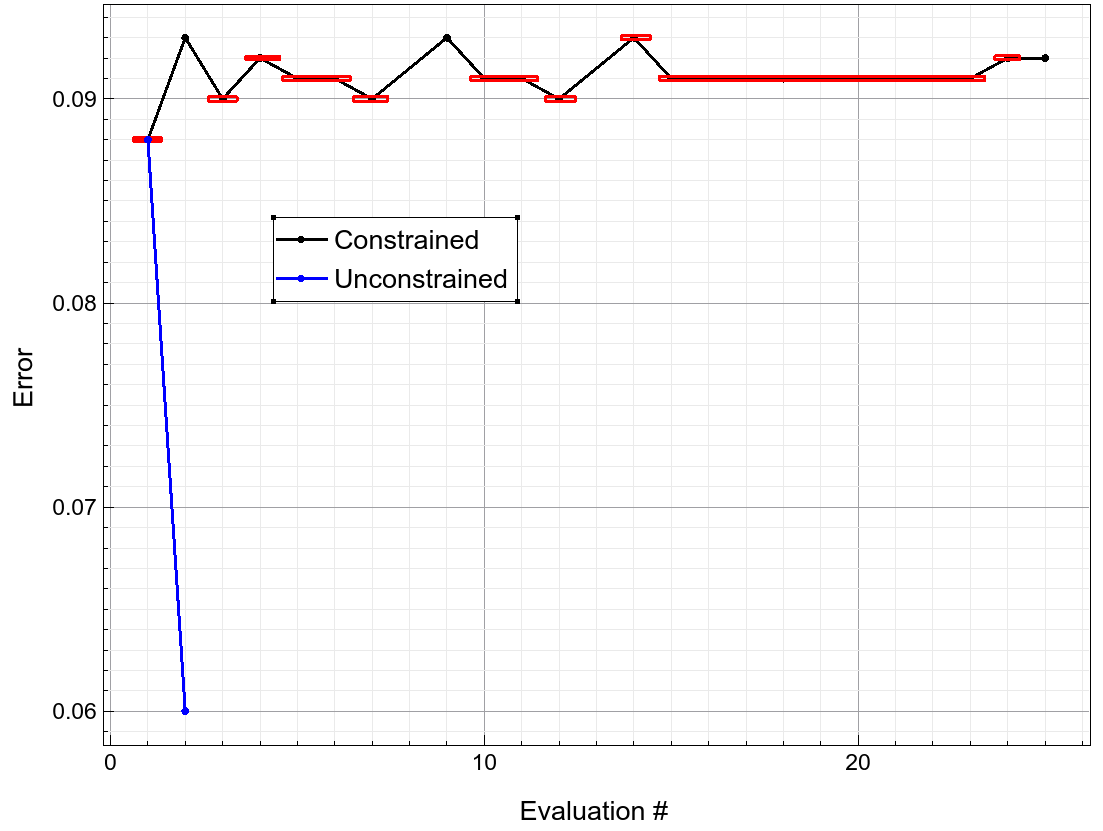
图 21. 初始搜索后局部最小化的收敛过程。蓝线对应于无约束最小化。(点击图片查看完整尺寸。)
10.3.4 优化结果 (Optimization Results)
每次优化任务(例如,搜索或优化)完成后,都会创建一个名称以 optimal_ 为前缀并附加任务编号的新场景。在此示例中,创建了两个最优场景:optimal_1 和 optimal_2。例如,图 22 显示了场景 optimal_1 的内容,该场景对应于初始搜索找到的最佳解。
优化后的 optimal_1 场景

图 22. 优化后的 optimal_1 场景。(点击图片查看完整尺寸。)
图 23 和图 24 显示了每一步(初始状态、搜索后、局部最小化后)前后 Id--Vd 特性和击穿曲线的变化。最终的局部最小化将导通电阻推至最小值,同时将击穿电压推向允许的最小值。
初始、optimal_1 和 optimal_2 场景的击穿曲线
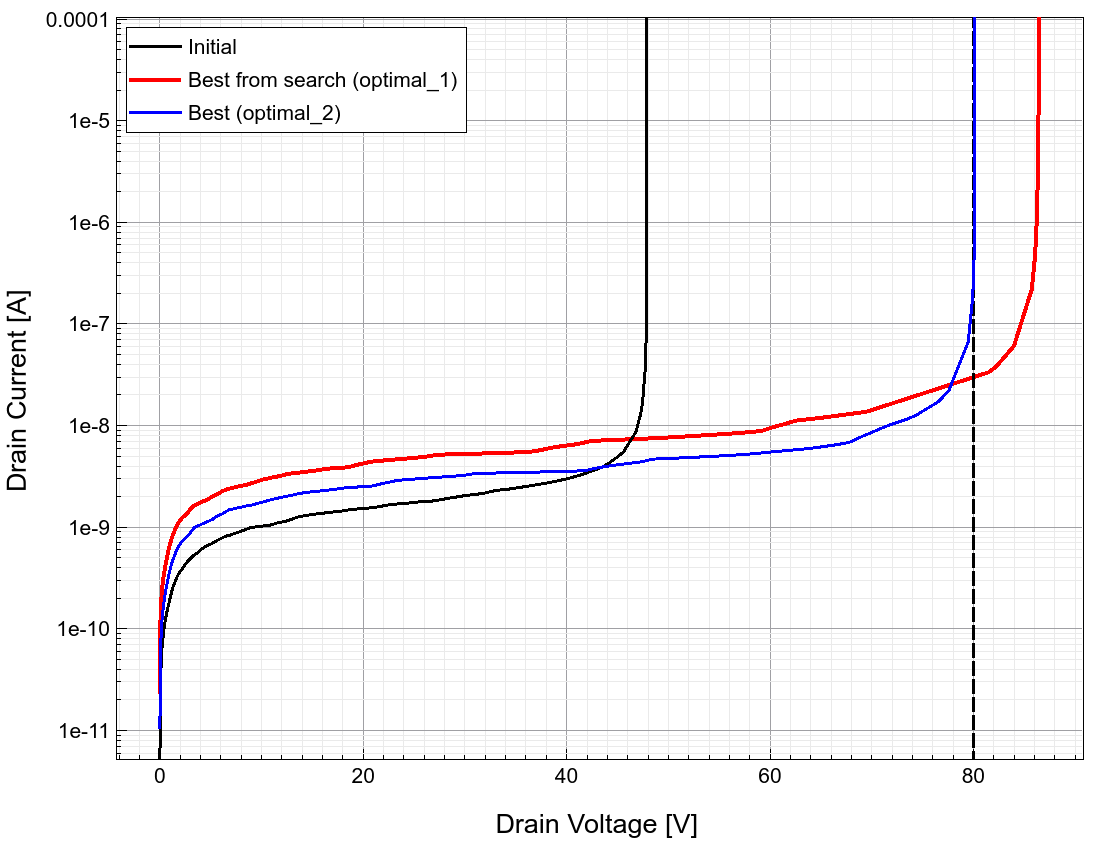
图 23. 初始、optimal_1 和 optimal_2 场景的击穿曲线。(点击图片查看完整尺寸。)
初始、optimal_1 和 optimal_2 场景的 Id--Vd 特性曲线
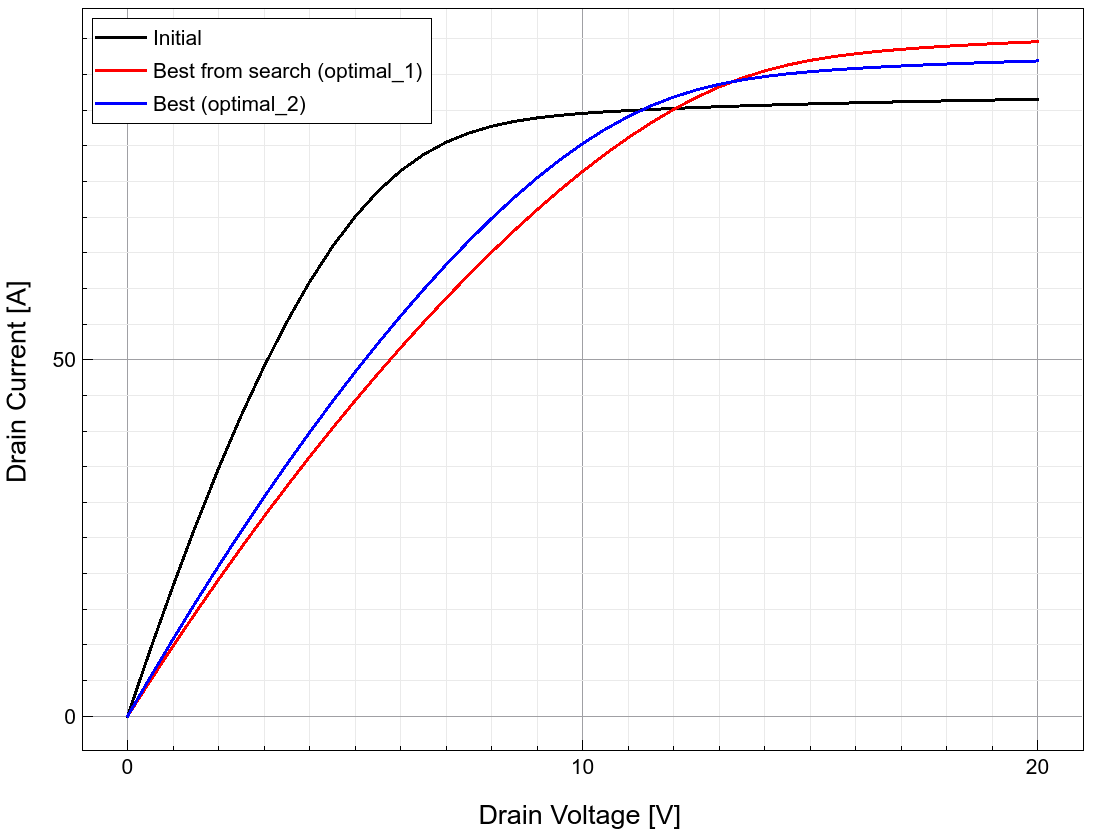
图 24. 初始、optimal_1 和 optimal_2 场景的 Id--Vd 特性曲线。(点击图片查看完整尺寸。)