数据结构之并查集

一、并查集的原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合，开始时，每个元素自成一个单元素集合，然后按一定规律将同一组的元素集合合并。在此过程中要反复用到查询某个元素归属于哪个集合的运算，适合于描述这类问题的抽象数据结构类型称为并查集（union-find-set）

比如作者有大学同学，高中同学，初中同学，他们彼此不认识。就会分为三个集合。

按10人来算，将其按编号分为0-9,

分为不同的团体

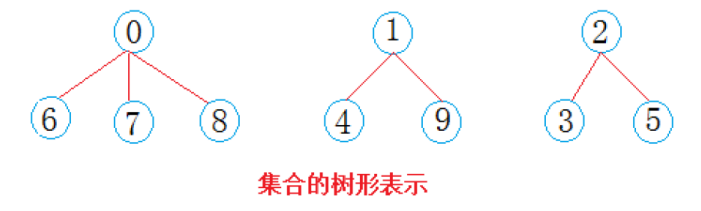
用数组来表示该树形关系，数组中的非负数代表其父节点，负数表示该结点为根结点，且该树形有abs（负数）个结点。

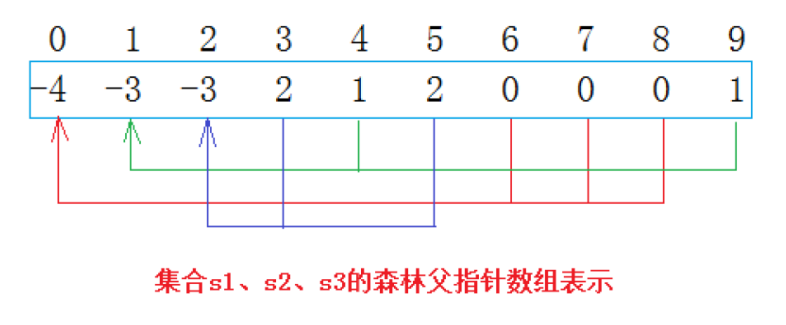
之后，机缘巧合下，大学同学和初中同学在一场聚会中认识了，就将其合并为一个集合。

通过以上例子可知并查集一般可解决以下问题：

1.查找元素属于哪一个集合

2.查看两个元素是否属于同一个集合

3.将两个集合归并为一个集合

4.得到集合的个数

二、并查集的实现

1.这里我使用map存储名字和其对应vector的下标，vector来存储其关系。

cpp 复制代码

class UnionFindSet{
public:
	UnionFindSet(int n) {
		v.reserve(n);
	}
private:
	vector<int> v;
	map<T,int> m;
};

2.push实现去添加新元素

cpp 复制代码

void push(T&& name) {
	v.push_back(-1);
	m[name] = v.size() - 1;
}
void push(const T& name) {
	v.push_back(-1);
	m[name] = v.size()-1;
}

这里实现右值引用和const左值引用两个版本

3.给一个元素，找见其元素所在集合的位置

cpp 复制代码

	//给一个元素，找见其元素所在集合的位置
	int UnionFind(const T& name) {
		if (m.count(name) == 0) {
			return -1;
		}
		else {
			//通过循环遍历，找见v[index]为负数的位置
			//该index就为根节点的位置
			int index= m.find(name)->second;
			while (v[index] >= 0) {
				index = v[index];
			}
			return index;
		}
	}

4.查找集合的个数

cpp 复制代码

	//集合的个数
	size_t Count()const {
		size_t count = 0;
		for (int i = 0; i < v.size(); i++) {
			if (v[i] < 0) {
				count++;
			}
		}
		return count;
	}

5.查找两个元素是否为同一个集合，并合并

cpp 复制代码

	//合并两个元素为同一个集合
	bool merge(const T& name1, const T& name2) {
		//查找两个元素是不是同一个集合
		int x1 = UnionFind(name1);
		int x2 = UnionFind(name2);
		if (x1 == x2) {//因为有相同的根节点，所以为同一个集合
			return false;
		}
		else {
			v[x1] += v[x2];//将v[x2]存储的内容加在v[v1]上更新新集合的结点数量
			v[x2] = x1;//将v[x2]指向父节点
			return true;
		}
	}
//也可合并多个元素，利用可变参数包
	template<class...Args>
	void merge(const T& name1, const T& name2, Args&&... args) {
		merge(name1, name2);
		if constexpr (sizeof...(args) > 0) {//constexpr可以在编译时检查，防止传参出现问题
			merge(name2, forward<Args>(args)...);//这里用完美转发去保持其右值属性不变。
		}
	}

三、并差集的应用

1.省份数量https://leetcode.cn/problems/number-of-provinces/description/

cpp 复制代码

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        vector<int> v;
        v.resize(isConnected.size(),-1);
        auto find=[&v](int index){//寻找根节点的数组下标
            while(v[index]>=0){
                index=v[index];
            }
            return index;
        };
        auto merge=[&v,&find](int a,int b){//合并两个集合
            int a1=find(a);
            int b1=find(b);
            if(a1!=b1){
                v[a1]+=v[b1];
                v[b1]=a1;
            }
        };
        for(int i=0;i<isConnected.size();i++){
            for(int j=0;j<isConnected.size();j++){
                if(isConnected[i][j]==1){//建立集合的关系
                    merge(i,j);
                }
            }
        }
        int count=0;
        for(int i=0;i<v.size();i++){
            
            if(v[i]<0){//判断"省份"的数量
                count++;
            }
        }
        return count;
    }
};

2.等式方程的可满足性https://leetcode.cn/problems/satisfiability-of-equality-equations/description/

cpp 复制代码

class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        vector<int> v;
        v.resize(26,-1);
        auto find=[&v](int index){
            while(v[index]>=0){
                index=v[index];
            }
            return index;
        };
        auto merge=[&v,&find](int x,int y){
            int x1=find(x);
            int y1=find(y);
            if(x1!=y1){
                v[x1]+=v[y1];
                v[y1]=x1;
            }

        };
        for(auto& e:equations){
            if(e[1]=='='){//先将等于关系建立起来
                merge(e[0]-'a',e[3]-'a');
            }
            
        }
         for(auto& e:equations){
        if(e[1]=='!'){//判断两个不等的元素是否有相等关系
                int x=find(e[0]-'a');
                int y=find(e[3]-'a');
                if(x==y){//有就返回失败
                    return false;
                }
            }
         }
        return true;//遍历结束返回成功
    }
};