时间序列预测实战：LSTM vs Transformer 在公共交通乘客量预测中的对比

小杨互联网2025-12-21 8:47

引言

时间序列数据在现实世界中无处不在，从每日天气测量到交通传感器读数，再到股票价格波动。当面对复杂的时间序列预测任务时，传统统计方法往往力不从心，而深度学习模型则展现出强大的潜力。本文将对比两种流行的深度学习架构------长短期记忆网络（LSTM）和Transformer，在公共交通乘客量预测任务中的表现。

实验设置与数据准备

数据集介绍

我们使用芝加哥公共交通乘客量数据集，该数据集记录了自2001年以来芝加哥公交和铁路系统的每日乘客量。考虑到COVID-19疫情对出行模式的剧烈影响，我们仅使用2019年12月31日之前的数据，以确保模型学习到相对稳定的出行模式。

数据预处理流程

python 复制代码 
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from sklearn.metrics import mean_squared_error, mean_absolute_error

# 数据加载与预处理
url = "https://data.cityofchicago.org/api/views/6iiy-9s97/rows.csv?accessType=DOWNLOAD"
df = pd.read_csv(url, parse_dates=["service_date"])

# 过滤疫情前数据
df_filtered = df[df['service_date'] <= '2019-12-31']
df = df_filtered

# 时间序列可视化
df.sort_values("service_date", inplace=True)
ts = df.set_index("service_date")["total_rides"].fillna(0)

plt.figure(figsize=(12, 6))
plt.plot(ts)
plt.title("芝加哥公共交通每日乘客量变化趋势")
plt.xlabel("日期")
plt.ylabel("乘客量")
plt.grid(True)
plt.show()

滑动窗口技术

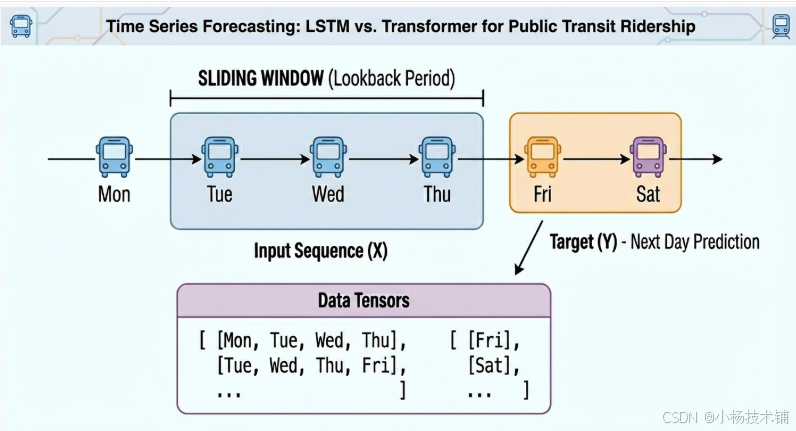
时间序列预测的关键步骤是将连续的时间序列数据转换为监督学习可用的格式。我们采用滑动窗口方法：

  • 输入序列（X）：连续N天的乘客量数据

  • 目标值（Y）：第N+1天的乘客量

python 复制代码 
def create_sequences(data, seq_len=30):
    """将时间序列转换为滑动窗口格式"""
    X, y = [], []
    for i in range(len(data)-seq_len):
        X.append(data[i:i+seq_len])
        y.append(data[i+seq_len])
    return np.array(X), np.array(y)

# 数据集划分
n = len(ts)
train = ts[:int(0.8*n)]  # 前80%作为训练集
test = ts[int(0.8*n):]   # 后20%作为测试集

# 转换为滑动窗口格式
SEQ_LEN = 30
X_train, y_train = create_sequences(train.values.astype(float), SEQ_LEN)
X_test, y_test = create_sequences(test.values.astype(float), SEQ_LEN)

# 转换为PyTorch张量
X_train = torch.tensor(X_train).float().unsqueeze(-1)
y_train = torch.tensor(y_train).float().unsqueeze(-1)
X_test = torch.tensor(X_test).float().unsqueeze(-1)
y_test = torch.tensor(y_test).float().unsqueeze(-1)

模型架构设计与实现

LSTM模型

长短期记忆网络（LSTM）是RNN的变体，专门设计用于解决长期依赖问题，在时间序列预测领域应用广泛。

python 复制代码 
class LSTMModel(nn.Module):
    """LSTM时间序列预测模型"""
    def __init__(self, hidden=32):
        super().__init__()
        self.lstm = nn.LSTM(1, hidden, batch_first=True)
        self.fc = nn.Linear(hidden, 1)
    
    def forward(self, x):
        out, _ = self.lstm(x)
        return self.fc(out[:, -1])  # 取最后一个时间步的输出

Transformer模型

Transformer最初用于自然语言处理，但其自注意力机制同样适用于捕捉时间序列中的长期依赖关系。

python 复制代码 
class SimpleTransformer(nn.Module):
    """简化版Transformer时间序列预测模型"""
    def __init__(self, d_model=32, nhead=4):
        super().__init__()
        self.embed = nn.Linear(1, d_model)
        enc_layer = nn.TransformerEncoderLayer(
            d_model=d_model, 
            nhead=nhead, 
            batch_first=True
        )
        self.transformer = nn.TransformerEncoder(enc_layer, num_layers=1)
        self.fc = nn.Linear(d_model, 1)
    
    def forward(self, x):
        x = self.embed(x)
        x = self.transformer(x)
        return self.fc(x[:, -1])  # 取最后一个时间步的输出

模型训练与评估

训练流程

python 复制代码 
def train_model(model, X, y, epochs=10, model_name="模型"):
    """统一训练函数"""
    model.train()
    optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
    loss_fn = nn.MSELoss()
    
    for epoch in range(epochs):
        optimizer.zero_grad()
        predictions = model(X)
        loss = loss_fn(predictions, y)
        loss.backward()
        optimizer.step()
        
        if (epoch+1) % 10 == 0:
            print(f"{model_name} - 轮次 {epoch+1}/{epochs}, 损失: {loss.item():.4f}")
    
    return model

# 模型实例化与训练
lstm_model = LSTMModel()
transformer_model = SimpleTransformer()

print("开始训练LSTM模型...")
lstm_model = train_model(lstm_model, X_train, y_train, epochs=50, model_name="LSTM")

print("\n开始训练Transformer模型...")
transformer_model = train_model(transformer_model, X_train, y_train, epochs=50, model_name="Transformer")

性能评估

我们使用两个常用指标评估模型性能：

  1. 均方根误差（RMSE）：对较大误差更敏感

  2. 平均绝对误差（MAE）：解释更直观

python 复制代码 
def evaluate_model(model, X_test, y_test, model_name="模型"):
    """评估模型性能"""
    model.eval()
    with torch.no_grad():
        predictions = model(X_test).numpy().flatten()
        true_values = y_test.numpy().flatten()
    
    rmse = np.sqrt(mean_squared_error(true_values, predictions))
    mae = mean_absolute_error(true_values, predictions)
    
    return predictions, rmse, mae

# 评估两个模型
print("评估模型性能...")
pred_lstm, rmse_lstm, mae_lstm = evaluate_model(lstm_model, X_test, y_test, "LSTM")
pred_trans, rmse_trans, mae_trans = evaluate_model(transformer_model, X_test, y_test, "Transformer")

print(f"\n{'='*50}")
print("模型性能对比:")
print(f"{'='*50}")
print(f"LSTM模型     - RMSE: {rmse_lstm:.1f}, MAE: {mae_lstm:.1f}")
print(f"Transformer模型 - RMSE: {rmse_trans:.1f}, MAE: {mae_trans:.1f}")
print(f"{'='*50}")

结果可视化与分析

python 复制代码 
# 预测结果可视化
plt.figure(figsize=(15, 10))

# 真实值 vs 预测值对比
plt.subplot(2, 1, 1)
plt.plot(y_test.numpy().flatten()[:100], label="真实值", alpha=0.7, linewidth=2)
plt.plot(pred_lstm[:100], label="LSTM预测", alpha=0.7, linestyle="--")
plt.plot(pred_trans[:100], label="Transformer预测", alpha=0.7, linestyle=":")
plt.title("模型预测结果对比（前100个样本）")
plt.xlabel("样本序号")
plt.ylabel("乘客量")
plt.legend()
plt.grid(True)

# 误差分布对比
plt.subplot(2, 1, 2)
errors_lstm = np.abs(y_test.numpy().flatten() - pred_lstm)
errors_trans = np.abs(y_test.numpy().flatten() - pred_trans)

plt.hist(errors_lstm, bins=50, alpha=0.5, label=f"LSTM (平均误差: {mae_lstm:.1f})")
plt.hist(errors_trans, bins=50, alpha=0.5, label=f"Transformer (平均误差: {mae_trans:.1f})")
plt.title("预测误差分布对比")
plt.xlabel("绝对误差")
plt.ylabel("频次")
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

讨论与结论

实验结果分析

在我们的实验中，两种模型表现出相似的性能：

  • LSTM模型：RMSE=1,350,000.8，MAE=1,297,517.9

  • Transformer模型：RMSE=1,349,997.3，MAE=1,297,514.1

虽然Transformer模型在数值上略优于LSTM，但差异微乎其微，在实际应用中可视为性能相当。

性能相似的可能原因

  1. 数据特性：单变量时间序列数据模式相对简单，两种模型都有足够能力捕捉其规律

  2. 预测任务简单：仅预测次日值，而非长期多步预测

  3. 模型简化：实验中使用了简化版的Transformer，未充分发挥其架构优势

实际应用建议

  1. 短期预测：对于简单的单步预测任务，LSTM可能是更经济的选择（计算资源需求较低）

  2. 长期依赖：如果需要捕捉更长的时间依赖关系，Transformer的自注意力机制可能更有优势

  3. 计算资源：Transformer通常需要更多计算资源，在部署时需要权衡性能与成本

扩展研究方向

  1. 多变量时间序列：考虑天气、节假日等多因素影响

  2. 长期预测：预测未来多天的乘客量，而非仅次日

  3. 模型融合：结合LSTM和Transformer的优势，设计混合架构

  4. 注意力可视化：分析Transformer关注的时间点，增强模型可解释性

总结

本文通过实际案例对比了LSTM和Transformer在时间序列预测任务中的表现。实验表明，对于相对简单的单变量短期预测任务，两种模型性能相近。在实际项目中，选择哪种架构应综合考虑任务复杂度、数据特性、计算资源等因素。

深度学习为时间序列预测提供了强大工具，但模型选择不应盲目追求最新技术，而应基于实际需求和数据特点做出理性决策。建议读者根据具体应用场景，通过实验确定最适合的解决方案。

相关推荐
upper20203 小时前
数据挖掘10
人工智能·数据挖掘
黑客思维者3 小时前
机器学习011:监督学习【回归算法】（多项式回归）-- 从“猜咖啡温度”到预测万物
人工智能·学习·机器学习·回归·线性回归·监督学习·多项式回归
IT·小灰灰3 小时前
豆包大模型1.8：Agent时代的多模态大脑——中国AI的跃迁时刻
人工智能
斯文by累3 小时前
Stable Diffusion 3.5 FP8：高效文生图技术革命
人工智能·stable diffusion
l1t3 小时前
豆包解读论文：将具有分支和循环控制流的命令式程序转换为标准SQL1999的公共表表达式
开发语言·数据库·人工智能·python·sql·postgresql·duckdb
～央千澈～3 小时前
AU针对AI音乐时间分析:改良人工智能: 最可能 (86%)需要如何处理？
人工智能
zhaodiandiandian3 小时前
守住伦理底线 破解生成式AI商业化的治理困局
人工智能
————A3 小时前
强化学习基础概念----状态、动作、策略、奖励
人工智能·python
黑客思维者3 小时前
机器学习010:监督学习【回归算法】（Lasso回归）-- 用“魔法剪刀”找到真正重要的信息
人工智能·学习·机器学习·回归·监督学习·回归算法·lasso
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05BongoCat - 跨平台键盘猫动画工具06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07jdk21下载、安装（Windows、Linux、macOS）08sqli-labs靶场通关笔记：第18-19关 HTTP头部注入09Open-AutoGLM Windows 安装部署教程10RedissonClient的配置解析