一、数据流的中位数(堆)
1、题目


2、分析
方法一:直接插入排序的方法进行排序,但是每次插入是O(k)的复杂度,k是现有节点数。然后取中位数。
方法二:两个堆排序,大根堆存放小于等于中位数的值,小根堆存放大于中位数的值。
- 始终要维护大根堆的最大值,小于小根堆的最小值。
- 两个堆要么长度相等(中位数是两个堆头的平均值),要么大根堆比小根堆多一个节点(中位数是大根堆头结点)。
如何维护:
- 若长度相等,插入小根堆,再把小根堆的最小值转移到大根堆(维持左比有多一个节点,维持左比右小)。
- 若长度不等,插入大根堆,再把大根堆的最大值插入小根堆(维持左、右长度相等,维持左比右小)。
时间复杂度:每次插入O(logk),k是现有结点数。空间复杂度O(k)。
3、代码
java
class MedianFinder {
private PriorityQueue<Integer> minHeap;
private PriorityQueue<Integer> maxHeap;
/**
初始化
*/
public MedianFinder() {
minHeap = new PriorityQueue<>(); // 小根堆
maxHeap = new PriorityQueue<>((a, b)->(b-a)); // 大根堆
}
/**
向有序序列插入一个值,始终保持
1. 左、右堆长度相等 或者 左比右堆长 1 个节点
2. 左堆最大值 小于等于 右堆最小值
*/
public void addNum(int num) {
// 若相等,插入右边小根堆,把最小值转移到左边大根堆
if(maxHeap.size() == minHeap.size()) {
minHeap.offer(num);
maxHeap.offer(minHeap.poll());
} else { // 否则,插入左边大根堆,把最大值转移到右边小根堆
maxHeap.offer(num);
minHeap.offer(maxHeap.poll());
}
}
public double findMedian() {
// 若相等,中位数是左、右头节点的平均
if(maxHeap.size() == minHeap.size()) return (maxHeap.peek()+minHeap.peek())/2.0;
// 若左大于右1个节点,中位数是左堆的头节点
return maxHeap.peek();
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/二、有效的括号
1、题目

2、分析
- 使用栈,每次拿到左括号入栈,拿到右括号弹出栈顶是否是左括号,如果不是(或者栈已经为空)则返回 false。
- 遍历字符串结束,如果栈不为空,则表示括号没有匹配完,返回false;经过层层筛选,返回true。
- 时间复杂度:遍历字符串,O(n)。空间复杂度:栈长度,O(n) + 括号类型总数。
3、代码
java
class Solution {
public boolean isValid(String s) { // s 仅由 '()[]{}' 组成
Stack<Character> stack = new Stack<>(); // 左括号栈
String left = "([{"; // 左括号字符
String right = ")]}"; // 右括号字符
int len = s.length();
for(int i = 0; i < len; i++) {
char ch = s.charAt(i);
if(left.indexOf(ch) > -1) { // 如果是左括号,则入栈
stack.push(ch);
}
else { // 弹出栈顶左括号,与当前右括号匹配
if(stack.isEmpty() || left.indexOf(stack.pop()) != right.indexOf(ch)) { // 栈为空、栈顶左括号不匹配,则无效
return false;
}
}
}
if(!stack.isEmpty()) { // 遍历结束,栈不为空,则无效
return false;
}
return true;
}
}三、最小栈
1、题目

2、分析
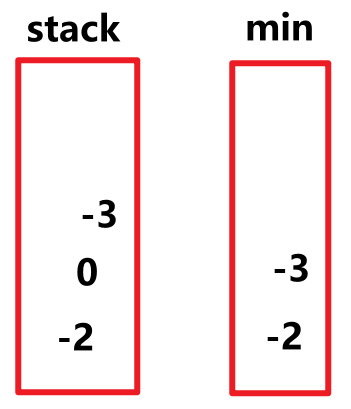
push 操作:
- 插入val,如果 stack 为空,最小值就是val,进入stack和min。
- 插入val,如果 val < min.top,最小值就是val,进入stack和min。
- 否则,仅进入stack。
pop 操作:
- 如果 stack 和 min 栈顶一样,那么 stack 弹出后,min 的栈顶不再是最小值,也弹出。
top操作:获取 stack栈顶。
getMin操作:获取min栈顶。
- 每个操作的时间复杂度都是O(1),空间复杂度为栈的O(n)。
3、代码
java
class MinStack {
private Stack<Integer> stack;
private Stack<Integer> minStack;
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
if(stack.isEmpty() || val <= minStack.peek()) { // 最小栈为空,或者 val ≤ 最小值栈栈顶,最小值栈要入
minStack.push(val);
}
stack.push(val); // 正常栈必入
}
public void pop() {
int val = stack.pop();
if(val == minStack.peek()) { // 如果正常栈栈顶 = 最小栈栈顶,要出最小栈
minStack.pop();
}
// if(stack.pop() == minStack.peek()) 不要这样写,两边都是 Integer 类型,比较的是对象的地址
// 上面的写法,因为 val 是 int,右边的 Integer 会自动拆箱
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/四、字符串解码
1、题目

2、分析
- 类似括号匹配,不是右括号就入栈,是右括号就开始出栈,拼接出 "字符串" 和 "重复次数"。把字符串重复后,再访回栈。
- 整个逻辑比较简单,麻烦的就是字符串转换。
- 时间复杂度:设解码后字符串长度为S,则O(S),空间复杂度也是O(S)。
3、代码
java
class Solution {
public String decodeString(String s) {
char[] chars = s.toCharArray();
Stack<String> stack = new Stack<>();
int len = chars.length;
StringBuilder ret = new StringBuilder();
StringBuilder tmp = new StringBuilder();
StringBuilder numStr = new StringBuilder();
int num;
for (int i = 0; i < len; i++) { // 遍历字符串
if (chars[i] != ']') { // 不是右括号就入栈
stack.push(String.valueOf(chars[i]));
} else { // 碰到右括号
// 把字符串弹出来
while (!"[".equals(stack.peek())) {
tmp.insert(0, (stack.pop())); // 栈弹出来是倒序,头插
}
stack.pop(); // 弹出左括号
// 把数字弹出来
while (!stack.isEmpty() && Character.isDigit(stack.peek().charAt(0))) numStr.insert(0, stack.pop());
num = Integer.parseInt(numStr.toString()); // 记录重复次数
for (int j = 0; j < num; j++) stack.push(tmp.toString()); // 字符串放入栈num次
// 清空,下次用
tmp.setLength(0);
numStr.setLength(0);
}
}
while (!stack.isEmpty()) ret.insert(0, stack.pop());
return ret.toString();
}
}五、每日温度
1、题目
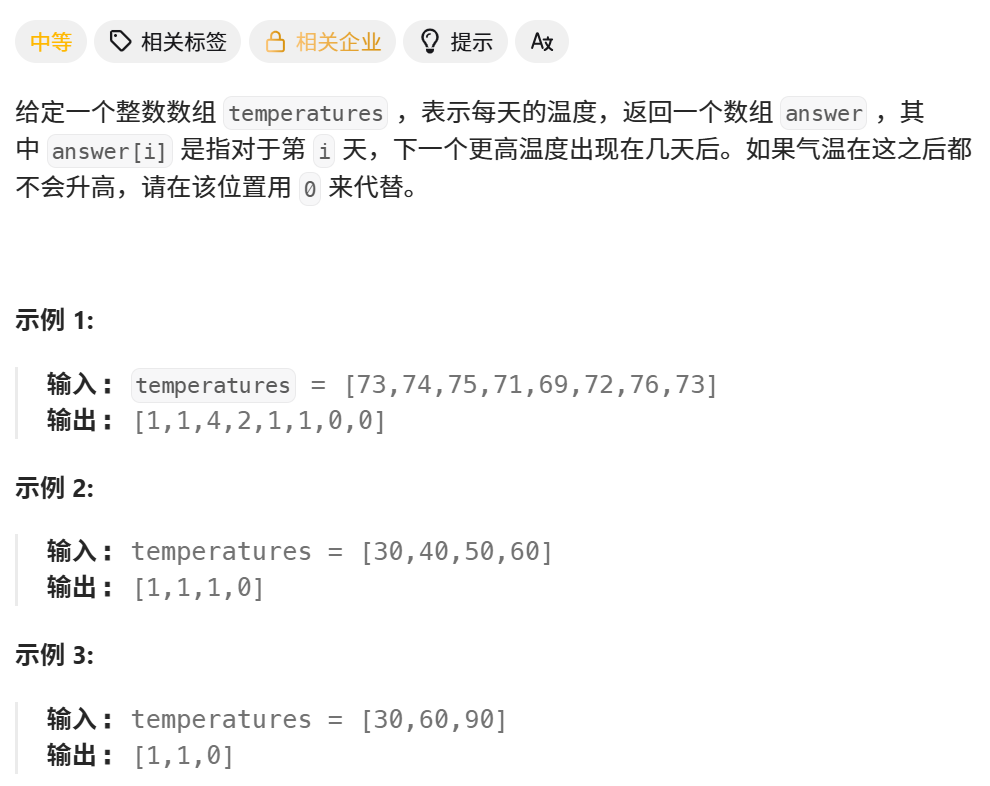
2、分析
方法一:暴力解法。i 从头遍历,j 再往后逐个找更大的。时间复杂度O(n),空间复杂度O(1)。
方法二:栈。
遍历数组:
- 栈为空,或者遍历元素 > 栈头,找到更大温度。弹出栈顶(对后面的温度来说已无用),计算天数。直到栈顶不再小于遍历数,把遍历数的下标放入栈。
- 遍历元素 <= 栈头,不是更大温度,直接入栈。
时间复杂度:O(n),空间复杂度:O(n)。
3、代码
java
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length;
int[] ret = new int[n];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int tmp = stack.pop();
ret[tmp] = i-tmp;
}
stack.push(i);
}
return ret;
}
} 六、柱状图中最大的矩形
1、题目
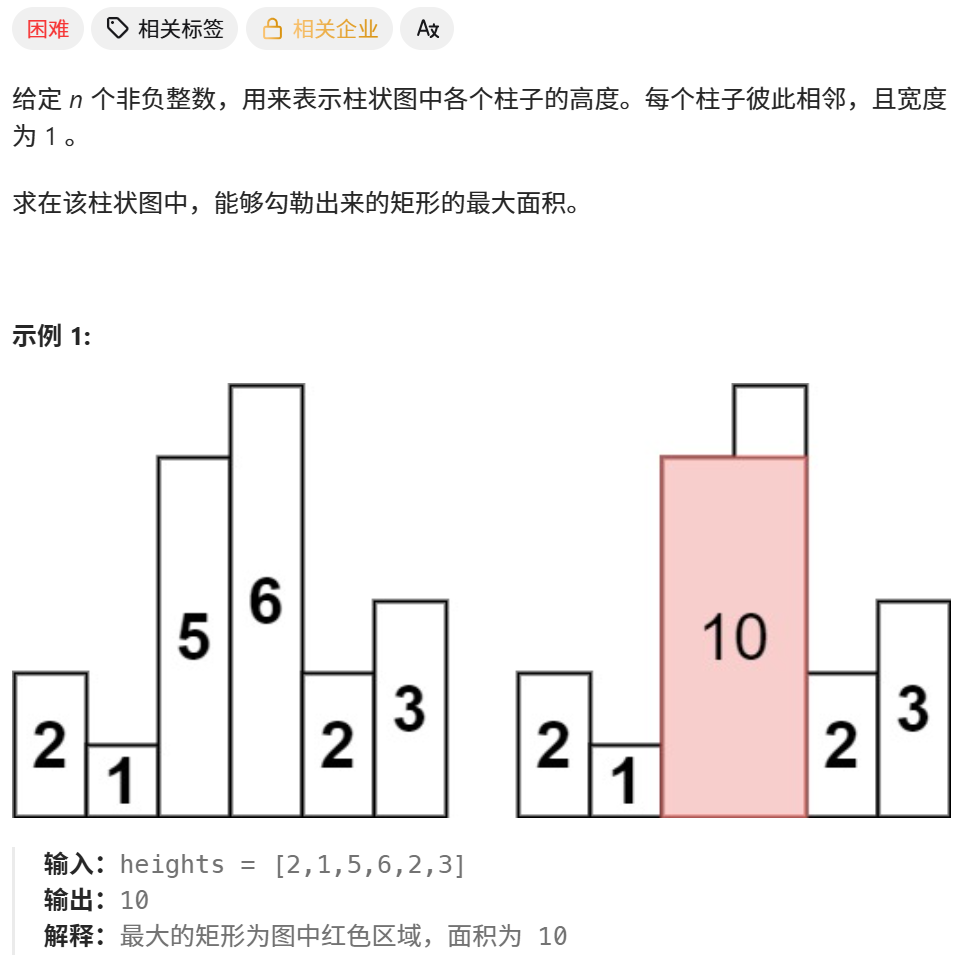
2、分析
方法一:暴力解法,遍历每个元素,依次以该元素为中心,向左右两边遍历,找小于该元素的左右边界。时间复杂度O(n^2)。
方法二:栈,左、右边界的下标数组。
- 遍历元素。
- 条件1:若元素 < 栈顶,栈顶找到右边界,栈顶出栈,直到不满足条件。
- 条件2:若元素 >= 栈顶,元素找到左边界(这条件1、2的执行不能调换顺序。比如现在栈内是 1 3 4,此时遍历到 2 。若调换,条件2不满足,条件1 弹出 3、4 找到右边界 2,1 是 2 的左边界却判定不到)。
- 元素入栈。
- 最后用左、右边界数组计算每个元素为高的面积,取最大面积。
- 时间复杂度O(n),空间复杂度 O(n)。
3、代码
java
class Solution {
public int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<>(); // 存元素下标
int n = heights.length;
int[] left = new int[n]; // 左边界下标
int[] right = new int[n]; // 右边界下标
int max = 0;
for(int i = 0; i < n; i++) {
left[i] = -1;
right[i] = n;
// 栈顶 找到右边界
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) right[stack.pop()] = i;
// heights[i] 找到左边界
if (!stack.isEmpty() && heights[stack.peek()] < heights[i]) left[i] = stack.peek();
stack.push(i);
}
// 找最大矩形
for (int i = 0; i < n; i++) max = Math.max(max, heights[i]*(right[i]-left[i]-1));
return max;
}
}