目录
一,拓扑排序简介
二,拓扑排序算法
1)普通拓扑排序算法普通拓扑排序算法)
2)拓扑和动态规划的结合
三,例题
蓝桥杯官网------走多远
题目描述
输入描述
输出描述
输入输出样例
[示例 1](#示例 1)
代码详解:
注:本文所有题目均来自蓝桥杯官网公开真题,仅做算法学习,代码皆由本人做出来并附上解析!
一,拓扑排序简介
拓扑排序是一种针对 "有向无环图" 的算法,用于解决一些有 "依赖关系" 的问题。拓扑序保证了当处理到某个点时,其所有的入点都已经处理过了。
例如下面这个图(来自蓝桥杯官网),拓扑序可以保证:处理点 2 之前,点 4 和点 6 都处理过。处理点 3 之前,点 2 和点 6 都处理过。
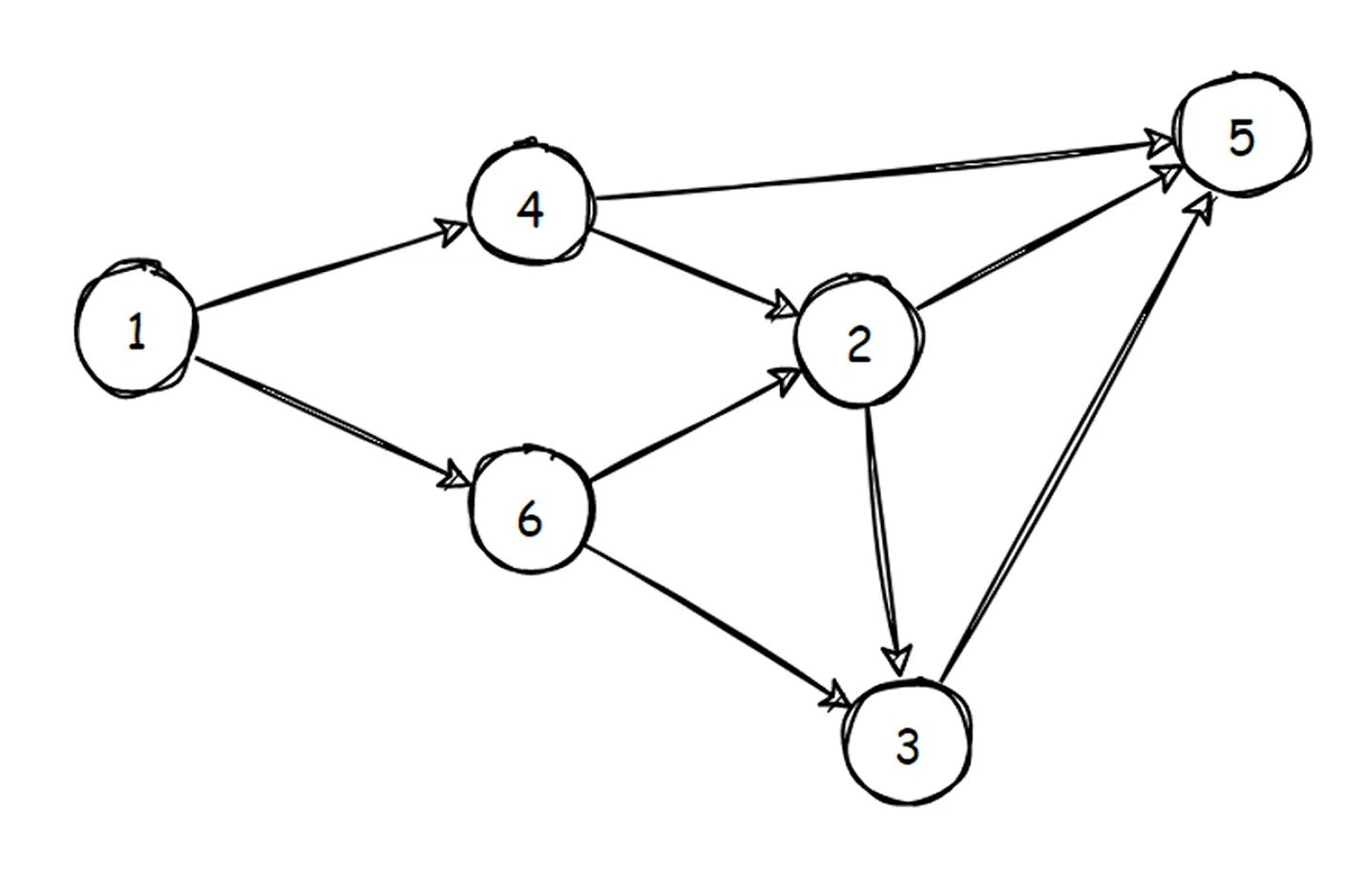
拓扑排序不一定是 "唯一" 的,只要满足拓扑关系即可。以下是一些下图(来自蓝桥杯官网)的可能拓扑序:
1, 4, 6, 2, 5, 7, 3\]\[7, 1, 4, 6, 2, 3, 5\]\[7, 1, 6, 4, 2, 5, 3\]...我们可以发现每个点的左侧包含它的所有入点。
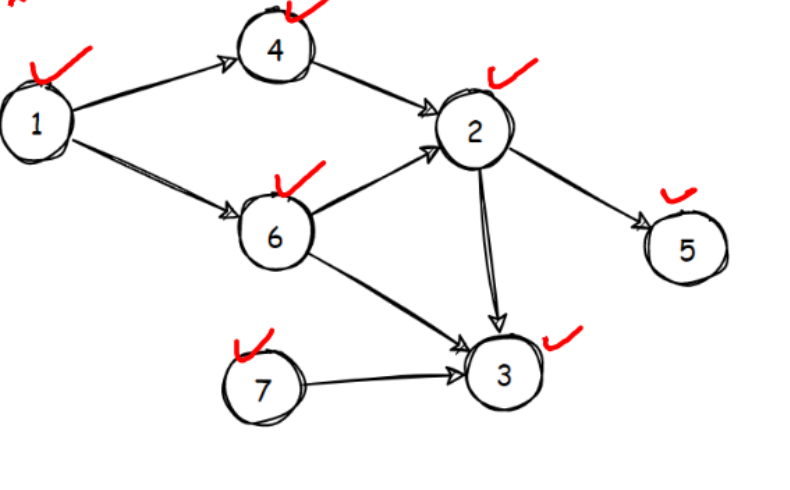
## 二,拓扑排序算法
### 1)普通拓扑排序算法
拓扑排序一般借助 queue(队列),使用类似 BFS 实现。先处理出每个点的入度,这个在读入边的时候处理。图一般用邻接表建立。拓扑排序一般借助 queue(队列),使用类似 BFS 实现。先处理出每个点的入度,这个在读入边的时候处理。图一般用邻接表建立。
代码:
```cpp
void topo()
{
queue q;
//将所有入度为0的点加入队列
for (int i = 1; i <= n; ++i)if (!ind[i])q.push(i);
while (q.size())
{
//取出队头的点x,此时它的入度一定为0,因为x是第一个进入队列的入度为0的点
int x = q.front(); q.pop();
for (const auto& y : g[x])
{
//处理边x->y
ind[y]--;//处理完成后y入度--
if (!ind[y])q.push(y);//如果y入度为0,说明y的所有入点已经处理完成了,直接入队
}
}
}
```
在main函数中,新增一条边:
```cpp
vectorg[N];
int main()
{
int n, m; cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int u, v; cin >> u >> v;
g[u].push_back(v);//添加u------->v有向边
ind[v]++;//v的入度+1
}
return 0;
}
```
### 2)拓扑和动态规划的结合
在枚举边 x-\>y 的时候,可以进行状态转移,于是可以和动态规划结合起来。这样的 DP 也叫做 DAG-DP(有向无环图上的动态规划)。状态转移一般只发生在枚举所有边的时候。
代码:
```cpp
void topo()
{
queue q;
//将所有入度为0的点加入队列
for(int i = 1;i <= n; ++ i)if(!ind[i])q.push(i);
while(q.size())
{
//取出队头的点x,此时它的入度一定为0
int x = q.front();q.pop();
for(const auto &y : g[x])
{
//处理边x->y
//在这里进行状态转移
//dp[y] = ...dp[x]...
ind[y] --;//处理完成后y入度--
if(!ind[y])q.push(y);//如果y入度为0,说明y的所有入点已经处理完成了,直接入队
}
}
}
```
## 三,例题
### 蓝桥杯官网------走多远
#### 题目描述
给定一个 n 个点,mm 条边的有向无环图,从入度为 0 点出发,顺着边最远能走多远,若不存在这样的点,输出 0。
#### 输入描述
第一行输入一个 n,m 。
接下来 m 行,每行输入俩个整数 u,v 代表有一条有向边从 u 到 v.
1≤n,m≤10\^6,1≤u,v≤n
#### 输出描述
输出一个整数表示最长距离。
#### 输入输出样例
##### 示例 1
输入:
2 1
1 2
输出:
1
解析:设状态 dp \[i\] 表示 i 点距离某一个起点的最远距离,状态转移的方向就是拓扑的顺序。假如存在一条边 x-\>y,则有dp \[y\]=max (dp \[y\], dp \[x\] + 1);初始时 dp \[i\]=0;
#### 代码详解:
```cpp
#include
#include
#include
using namespace std;
using ll=long long;
const int N=1e6+9;
int n,m,dp[N],ind[N];//入度
vectorg[N];
void topo()
{
queueq;
//走入度为0的点(找所有起点)
for(int i=1;i<=n;i++)
{
if(!ind[i]) q.push(i);
}
//只要队列不为空,就不断拓展
while(q.size())//或者写while(!q.empty())
{
//取出队头元素,并pop掉(很重要)
int x=q.front();q.pop();
//枚举所有边
for(const auto &y:g[x])
{
dp[y]=max(dp[y],dp[x]+1);
if(--ind[y]==0)q.push(y);//从x往下走,只走入度为0的,那么每次走下一步,由于上一步已经删除
//则下一步的入度就要减1,此时若下一步入度为0就走,并且入队
}
}
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y;cin>>x>>y;
ind[y]++;//入度增加
g[x].push_back(y);
}
topo();//拓扑排序
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,dp[i]);
cout<
