【计算机视觉】04_角点

核心在于回答一个问题：我们如何在图像中找到独特且可重复使用的点（特征）？这是实现图像配准、拼接和识别的基础。

为什么需要局部特征？

局部特征（例如角点和团块）是计算机视觉中用于连接不同视角图像的关键"粘合剂"：

全景图拼接： 提取特征、匹配特征、配准图像是自动化全景图拼接的三大步骤。
应用广泛： 特征点可用于图像配准、3D 重建、运动跟踪（如用于增强现实）、目标识别以及机器人/汽车导航等领域。
局部特征的优点： 局部性意味着特征对遮挡和杂乱场景具有鲁棒性。它们数量大，一张图中可以有成百上千个；同时，它们具有判别性，能够区分大量的目标。

提取特征的主要步骤包括：

特征检测： 确认特征点（找到它）,。
特征描述： 围绕每个特征点提取向量（表示它）,。
特征匹配： 确定两个视角特征描述子之间的对应关系（匹配它）。

局部特征的优点

局部性
特征是局部的，对遮挡和杂乱场景具有鲁棒性
数量大
一张图中有成百上千的局部特征
判别行
可以区分大量目标
效率
可以获得实时效果

什么是好的特征？

一个好的特征点必须具有唯一性 ，即它是一个独特的图像区域 ，能够获得与其他图像无歧义的匹配

唯一性的局部度量（滑动窗口分析）

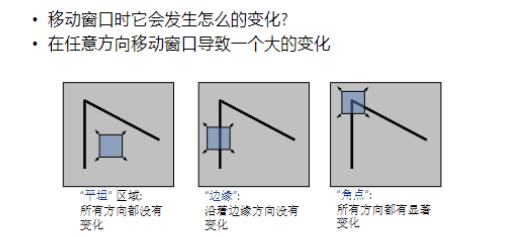
Harris 角点检测：数学原理

Harris 角点检测器就是基于上述"在所有方向上移动窗口都会导致一个大的变化"的思想构建的。

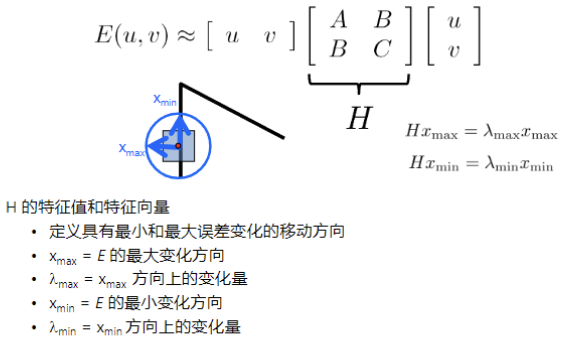
A. 二阶矩矩阵 HHH

Harris 算子的核心是通过泰勒展开式的一阶近似，将 SSD 误差 E(u,v)E(u, v)E(u,v) 局部近似为一个二次型。

这个二次型与一个 2×22 \times 22×2 的二阶矩矩阵 HHH 相关联，这个 HHH 矩阵包含了图像在 xxx 和 yyy 方向的梯度平方和交叉乘积的局部平均,。

E(u,v)≈[uv]H[u v]E(u, v) \approx \begin{bmatrix} u & v \end{bmatrix} H \begin{bmatrix} u \ v \end{bmatrix}E(u,v)≈[uv]H[u v]

这里 Ix,IyI_{x}, I_{y}Ix,Iy为梯度

A=∑Ix2A = \sum I_x^2A=∑Ix2: 把窗口里所有像素的水平梯度的平方加起来。
C=∑Iy2C = \sum I_y^2C=∑Iy2: 把窗口里所有像素的垂直梯度的平方加起来。
B=∑IxIyB = \sum I_x I_yB=∑IxIy: 把窗口里每个像素的"水平梯度 ×\times× 垂直梯度"加起来

B. 特征值与角点分类

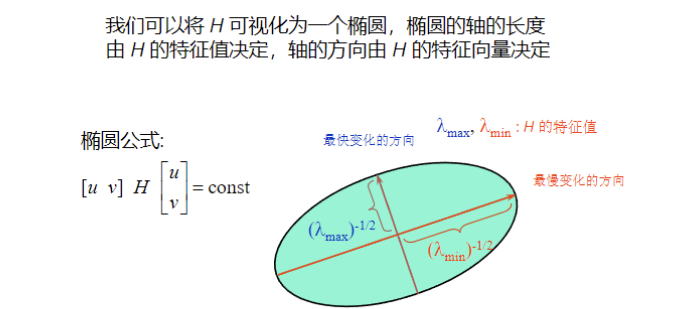
矩阵 HHH 的特征值 (λ1\lambda_1λ1 和 λ2\lambda_2λ2) 决定了误差二次型的形状：

特征值 决定了椭圆轴的长度，即最小和最大误差变化的量。
特征向量 决定了轴的方向，即最小和最大变化的方向 。

利用 λ1\lambda_1λ1 和 λ2\lambda_2λ2 的值，可以对图像点进行准确分类:

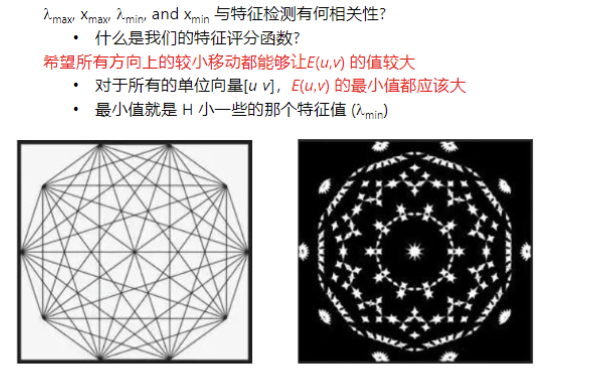
特征值关系区域类型图像变化λ1\lambda_1λ1 和 λ2\lambda_2λ2 均小"平坦"区域 EEE 几乎是常量。λ1≫λ2\lambda_1 \gg \lambda_2λ1≫λ2 （或反之）"边缘" EEE 仅在一个方向上有大变化。λ1\lambda_1λ1 和 λ2\lambda_2λ2 均大，且 λ1≈λ2\lambda_1 \approx \lambda_2λ1≈λ2**"角点"** EEE 在所有方向上都有增长变化。为了找到角点，我们希望所有方向上的最小移动都能让 E(u,v)E(u, v)E(u,v) 的值较大，这意味着 HHH 较小的那个特征值 (λmin\lambda_{min}λmin) 必须大。

角点检测总结

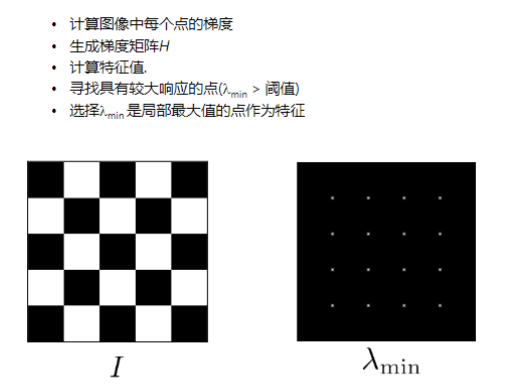
C. Harris 算子（R Score）

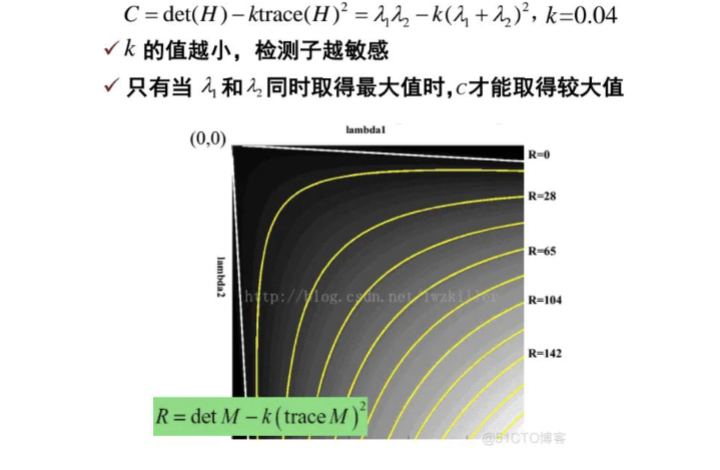
虽然 λmin\lambda_{min}λmin 是理论上最佳的角点评分，但 Harris 算子（Harris Detector）使用了一个计算上更简单的近似公式 RRR。

R=det⁡(H)−αtrace⁡(H)2R = \operatorname{det}(H) - \alpha \operatorname{trace}(H)^2R=det(H)−αtrace(H)2

通过计算每个像素的 RRR 值，并寻找 RRR 值大且是局部最大值 的点，即可检测出 Harris 特征（角点）。

或者写成特征值的形式：

R=λ1λ2−k(λ1+λ2)2R = \lambda_1 \lambda_2 - k (\lambda_1 + \lambda_2)^2R=λ1λ2−k(λ1+λ2)2

kkk 是什么？ 是一个经验常数，通常取 0.040.040.04 到 0.060.060.06。

这个函数 RRR 怎么评分？

如果是角点 (λ1,λ2\lambda_1, \lambda_2λ1,λ2 都很大)：
- 乘积 λ1λ2\lambda_1 \lambda_2λ1λ2 会变得超级大（远大于和的平方）。
- 结果：RRR 是很大的正数。
如果是边缘 (一个大一个小)：
- 假设 λ1\lambda_1λ1 很大，λ2≈0\lambda_2 \approx 0λ2≈0。那么乘积 ≈0\approx 0≈0，但和的平方很大。
- 结果：RRR 是很大的负数。
如果是平坦区域 (都小)：
- 乘积和小都很小。
- 结果：RRR 接近 0。

导数加权

这张图的核心思想是：为了让角点检测更稳定、且不管图片怎么旋转都能检测出来（旋转不变性），我们不能搞"大锅饭"（方框滤波），而要搞"核心制"（高斯加权）。

旧方法： 所有人平等投票 →\rightarrow→ 容易受干扰，对旋转敏感。
新方法： 离中心近的 VIP 票数多，离得远的票数少 →\rightarrow→ 结果更稳定，且高斯函数是圆的，转起来也没影响。

1. 上半部分：为什么简单的窗口不好？

(Top Equation: Simple Window)

H=∑(x,y)∈W[Ix2IxIyIxIyIy2]H = \sum_{(x,y) \in W} \begin{bmatrix} I_x^2 & I_x I_y \\ I_x I_y & I_y^2 \end{bmatrix}H=(x,y)∈W∑[Ix2IxIyIxIyIy2]

做法： 这里用的是最普通的求和 (∑\sum∑)。这意味着窗口 WWW 里（比如 5×55 \times 55×5 的方框）的每一个像素，权重都是 1。
问题 (In practice, not good)：
- 不够圆（各向异性）： 你的窗口是个正方形的盒子。如果一张图片旋转了 45 度，原本在正方形角上的像素可能就跑出去了。这意味着你的算法对"旋转"非常敏感，转一下图片，角点可能就找不到了。
- 噪声干扰： 窗口边缘的像素影响太大。只要一个噪点滑进这个方框的边缘，它立刻拥有 100% 的话语权，会导致计算结果突然跳变。

2. 下半部分：导数加权 (Derivative Weighting)

(Bottom Equation: Gaussian Window)

H=∑(x,y)∈Wwx,y[Ix2IxIyIxIyIy2]H = \sum_{(x,y) \in W} \color{red}{w_{x,y}} \begin{bmatrix} I_x^2 & I_x I_y \\ I_x I_y & I_y^2 \end{bmatrix}H=(x,y)∈W∑wx,y[Ix2IxIyIxIyIy2]

做法： 引入了一个权重系数 wx,yw_{x,y}wx,y。
图示 (右下角的发光圆点)： 那个黑背景中间亮白色的图，就是一个高斯核 (Gaussian Kernel)。
- 中心最亮 (权重最大)： 靠近窗口中心的像素，最能代表"这里的情况"，所以给它们最高的权重。
- 边缘变暗 (权重衰减)： 离中心越远的像素，关系越疏远，权重逐渐降低。