数据挖掘11--主成分分析PCA
首先介绍预备知识,不看也行
一、维归约(Dimensionality Reduction),也叫降维
高维数据映射到一个低维空间,保留原始数据中的重要结构、关系和信息
多选题

答案:ABCD
二、降维方法
1.特征提取方法:
典型方法有主成分分析、线性判别分析、自编码器等,将原始特征创造出全新的、数量更少的特征。
2.特征子集选择(Feature subset selection)
(1)定义:
从原有的数据中删除不重要或不相关的属性,或者对属性重组来减少属性的个数。
(2)目的:
找到最小的属性子集,且该子集的概率分布尽可能接近原数据集的概率分布
(3)寻找最小属性子集的方法:
1)逐步向前选择
2)逐步向后选择
3)向前选择与向后删除结合
3.聚集(Aggregation):
平均值、求和、最大值、最小值
4.抽样
现在开始介绍今天的主题PCA
二、PCA(Principal Component Analysis)
1.PCA的原理:
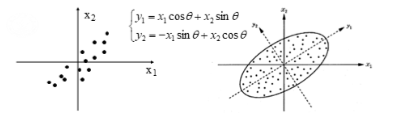
找到一组新的正交基(主成分),使得数据在这组基上的投影具有最大方差。
方差越大,说明数据在这个方向上越"分散",包含的信息越多。
举个极端情况的例子帮助理解:

数据都分布在水平直线上。
现在要用一维数据描述,选择X轴还是Y轴。
肯定是选择X轴,因为如果用Y轴描述,这些值投射在Y轴上值相同,无法区分。
现在您能理解分散的意义了吧
再举个二维的例子:
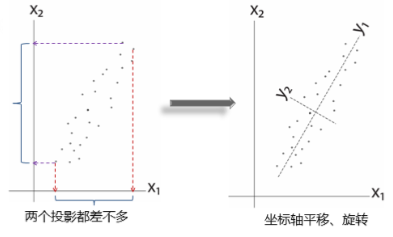
显然,y1 、y2更好。
2.PCA的几何意义:
从上面的极端例子,我们可知道主成分分析从几何上看,就是寻找数据在哪个方向上最分散。
换成专业词汇表达就是,
寻找主轴
数学点表达就是
p维空间m维椭球体的主轴问题(m < p)
那么在数学上主轴是什么呢?也就是主轴的计算方法?
各个主轴是相关矩阵的m个较大的特征值对应的特征向量
那什么是相关矩阵呢?
3.相关矩阵(Correlation Matrix)
第 i 行第 j 列的元素表示变量 Xi 与变量 Xj 之间的相关系数。
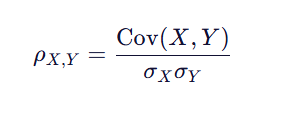

自然,
相关矩阵是一个对称方阵,因为第 i 行第 j 列的元素和第 j 行第 i 列的元素都是变量 Xi 与变量 Xj 之间的相关系数。
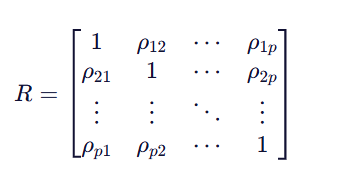
其中,
(1)对角线上的元素是每个变量与自身的相关系数,恒为 1。
(2)非对角线元素取值范围在 [−1,1]。
(3)1:完全正相关;0:无线性相关;-1:完全负相关。
4.多选题
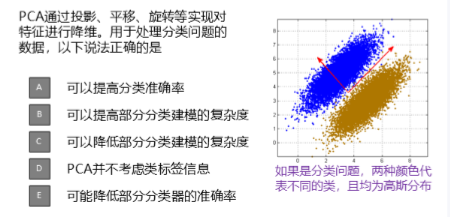
答案:CDE
理由:
D正确:
PCA 是一种无监督学习方法,它只关注数据本身的方差结构,不关心样本的标签。
它的目标是找到能最大化数据方差的方向,而不是让不同类别尽可能分开。
所以,即使有两类数据(如图中蓝橙两色),PCA 也不会刻意去"区分"它们,只会找整体数据变化最大的方向。
这正是 PCA 的局限性:它可能将原本可分的类别投影到一起,从而导致分类性能下降。
C正确:
例如:原来有 100 维特征,用 PCA 降到 10 维,那么后续分类器(如 SVM、逻辑回归)需要拟合的参数大大减少,模型复杂度下降。
特别是在高维小样本场景下,PCA 有助于防止过拟合。
所以这个说法也正确。
B错误:
PCA 是降维,通常减少输入维度,这会让模型更简单(如线性分类器参数变少);
所以一般会降低模型复杂度,而不是提高。
此说法错误。
E正确
如图所示:两类数据虽然分离,但若 PCA 投影方向不是沿着类间差异最大方向(而是沿着总体方差最大方向),可能导致两类在新空间中重叠更多。
因此,有可能降低分类准确率,尤其是在类别分布不对称或非线性可分时。