介绍线性回归
线性回归核心
本质:数理统计中用回归分析量化变量间定量依赖关系的方法,聚焦"有方向的因果影响"。
相关关系的两类:
因果关系:变量有"原因→结果"方向,需分自变量(因)/因变量(果),线性回归用它算"自变量每变1单位,因变量平均变多少"(权重θ体现影响大小与方向)。
平行关系:变量仅"伴随变化"无因果(,不区分自变量/因变量,只用相关系数r。
关键区别:回归是"因果建模"(定量算影响),相关是"关联描述"(只说紧密度);线性回归是回归分析在"线性关系"下的具体实现。
一元线性回归模型
一元线性回归模型
定义:仅含1个自变量(如x)与1个因变量(y)的线性模型,是线性回归的最简形式。
模型:y = θ₀ + θ₁x + ε
θ₀:截距(x=0时y的基准值);
θ₁:斜率(x每变1单位,y的平均变化量);
ε:随机误差(未解释的噪声)。
目标:用最小二乘法估计θ₀、θ₁,让预测值最贴合真实值。
求解:
θ₁ = 协方差(x,y) / 方差(x)(反映x与y的关联强度与方向);
θ₀ = y的平均值 - θ₁×x的平均值(直线过样本中心(x̄,ȳ))。
本质:用直线量化"x对y的线性影响方向与大小",是多元线性回归的基础。
多元线性回归模型
定义:含多个自变量(如x₁、x₂...xₙ)与1个因变量(y)的线性模型,是现实最常用的线性回归形式。
模型:y = θ₀ + θ₁x₁ + θ₂x₂ + ... + θₙxₙ + ε
θ₀:截距(所有自变量为0时y的基准值);
θ₁~θₙ:权重(每个自变量对因变量的边际影响:该自变量每变1单位,y的平均变化量);
ε:随机误差(未解释的噪声)。
矩阵简化:y = Xθ + ε(X是含全1列的特征矩阵,θ是权重向量)。
目标:用最小二乘法估计θ,最小化预测误差平方和。
求解:若XᵀX可逆,θ的估计值为 (XᵀX)⁻¹Xᵀy(矩阵闭式解)。
本质:量化多个自变量对因变量的联合线性影响,需避免自变量间高度相关(多重共线性)。
误差项分析
误差项的本质与作用
定义:线性回归中,未被自变量解释的因变量变异,公式为 y=预测值+ε(ε即误差项)。
来源:测量误差、未纳入模型的自变量、变量间的非线性关系、随机噪声等。
核心作用:误差项越小,模型对数据的"解释力"越强;但误差不可能为0(否则模型会拟合噪声,导致过拟合)。
误差项的关键假设
普通最小二乘法(OLS)估计的参数要"无偏、有效",需满足误差项的4个假设:
零均值:E(ε) = 0(误差无系统性偏向,模型预测整体无偏);
同方差:Var(ε_i) = σ²(所有样本的误差波动大小一致,不随自变量变化);
无自相关:Cov(ε_i, ε_j) = 0(i≠j,样本间误差独立,无"连锁反应");
注:Cov(ε_i, ε_j)表示第i个样本与第j个样本的误差项的协方差
正态分布:ε_i ~ N(0, σ²)(误差服从正态分布,用于参数显著性检验等统计推断)。
误差项的诊断方法
需通过可视化或统计检验,判断误差项是否满足假设:
残差图(最直观):
残差 vs 预测值:散点随机分布(无明显趋势/"漏斗形")→ 同方差成立;若呈"漏斗形"(方差随预测值增大而变大)→ 异方差。
残差 vs 自变量:散点随机分布→ 线性关系合理;若呈曲线趋势→ 需补充非线性项(如x²)。
统计检验:
异方差:White检验、Breusch-Pagan检验(p值<0.05则存在异方差);
自相关:Durbin-Watson检验(值接近2→无自相关;<1或>3→存在自相关);
正态性:Shapiro-Wilk检验(p值>0.05→符合正态)、Q-Q图(点越贴近直线→正态性越好)。
误差项异常的后果与修正
若误差项违反假设,会导致模型结论不可靠,需针对性修正:
异方差(误差方差随预测值变化):
后果:参数估计仍无偏,但标准误不准确(易导致"假阳性"显著性结论);
修正:加权最小二乘法(WLS)、对变量取对数(压缩方差)。
自相关(样本间误差相关,如时间序列数据):
后果:参数估计无偏但效率低(标准误偏小,易高估显著性);
修正:广义最小二乘法(GLS)、加入滞后项(如y_{t-1})。
非正态性(误差不服从正态分布):
后果:小样本下假设检验失效;
修正:Box-Cox变换(调整变量分布)、使用鲁棒标准误(不依赖正态假设)。
误差项的现实意义
误差项的大小反映模型的"未知空间":误差越小,模型能解释的现实规律越多,但需避免过度追求小误差(可能拟合噪声,降低泛化能力)。
误差项是模型"局限性"的体现:若误差持续过大,需反思是否遗漏关键自变量、是否应改用非线性模型(如多项式回归、树模型)。
总结:误差项是线性回归的"隐形考官"------需通过诊断确保其满足假设,否则模型结论可能误导决策;同时,误差项的大小也提示模型的改进方向。
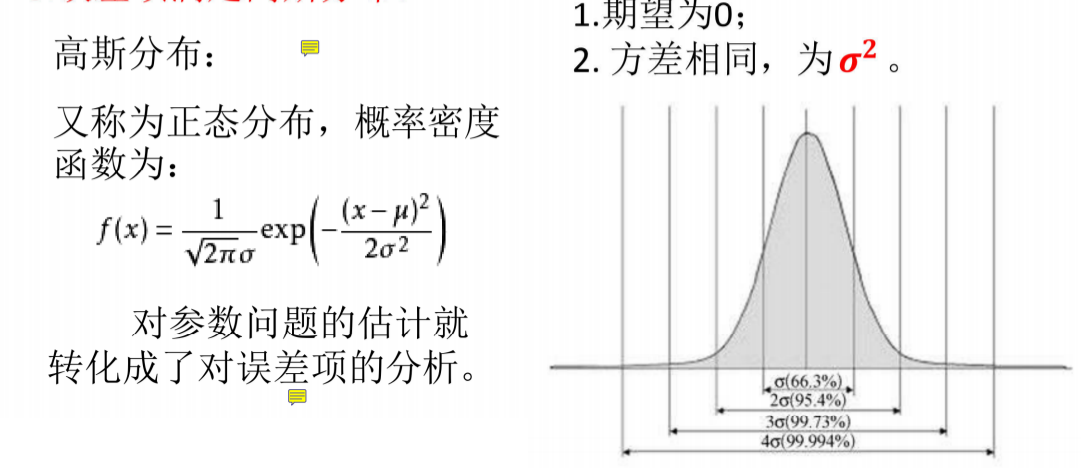
误差项满足高斯分布
误差项满足高斯分布(正态)是线性回归的关键假设,即εᵢ~N(0,σ²),能让参数估计更有效、假设检验(如t/F检验)和置信区间计算更可靠。可用Q-Q图(点近直线)或Shapiro-Wilk检验(p>0.05)判断是否正态。若不满足,会导致检验失效、置信区间不准,小样本更明显。修正可试变量变换(如对数)、鲁棒标准误或更换模型(如非线性/广义线性模型)。它是统计推断的基石,需验证,不满足则调方法保可靠。
极大似然估计
定义:一种参数估计方法,核心思想是:选一组参数,让"观测到当前样本数据"的概率(似然)最大。
基本逻辑:
先假设数据服从某分布(如线性回归中误差项εN(0,σ²),则yN(Xθ,σ²));
写出"观测到所有样本"的似然函数(各样本概率的乘积,因样本独立);
对似然函数取对数(简化计算,乘法变加法),求偏导找极值点,得最大似然估计值。
线性回归中的应用:
当线性回归满足"误差正态"假设时,极大似然估计的结果与最小二乘法(OLS)完全一致(θ的估计值相同),但MLE更通用(可扩展到非线模型、非正态误差)。
优势:理论严谨,能自然融入先验信息(贝叶斯MLE),适用于复杂模型(如逻辑回归、深度学习);
局限:依赖"数据分布假设",若假设错(如误差非正态),估计可能失效。
一句话总结:MLE是"让样本出现概率最大的参数"估计法,线性回归中(误差正态时)等价于OLS,是统计/机器学习的核心估计工具。
似然函数求解
数据与分布假设
线性回归模型:y = Xθ + ε(X为特征矩阵,θ为权重向量,ε为误差项)。
假设误差项独立同分布且正态:ε_i ~ N(0, σ²),则因变量y_i ~ N(X_iθ, σ²)(X_i是第i个样本的特征行向量)。
- 似然函数(联合概率)
似然函数L(θ, σ²)是"给定参数(θ, σ²)时,观测到所有样本y₁,...,y_m"的概率(样本独立,概率相乘):
L(θ, σ²) = ∏[i=1 to m] [1/√(2πσ²)] * exp(-(y_i - X_iθ)²/(2σ²))
- 对数似然(简化计算)
取自然对数(乘积变求和,单调性不变):
ln L(θ, σ²) = -m/2 * ln(2π) - m/2 * ln(σ²) - 1/(2σ²) * ∑[i=1 to m] (y_i - X_iθ)²
最大化对数似然(求偏导找极值)
对θ和σ²分别求偏导,令偏导为0,解出最优估计:
对θ求偏导:
仅最后一项含θ,求导并令其为0:
∂ln L/∂θ = (1/σ²) * ∑[i=1 to m] (y_i - X_iθ)X_i = 0
化简得矩阵形式:X^T(y - Xθ) = 0,解得:
对σ²求偏导:
令∂ln L/∂σ² = 0,解得:
σ²_MLE = (1/m) * ∑[i=1 to m] (y_i - X_iθ_MLE)² (分母为样本量m)
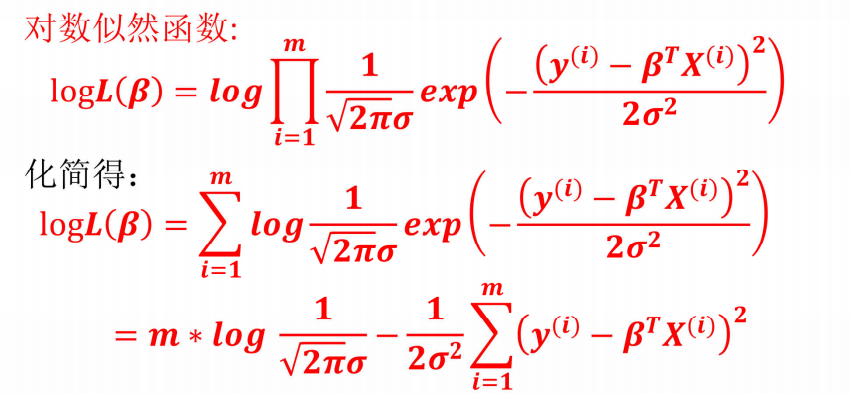

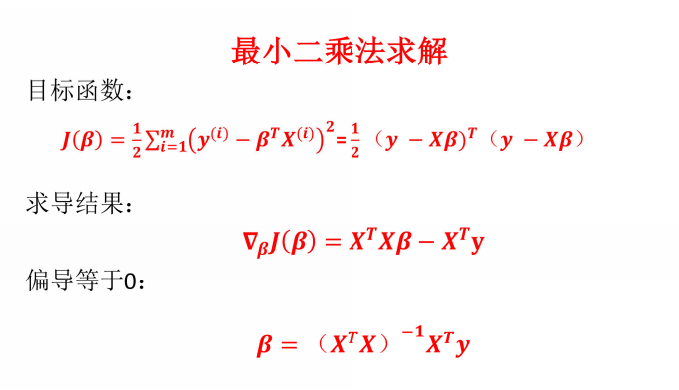
相关系数
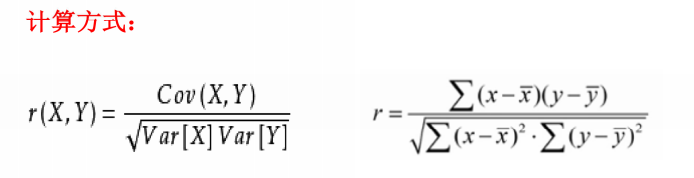
Cov(X,Y)为X与Y的协方差
Var[X]为X的方差
Var[Y]为Y的方差
相关系数的解释:
-
|r|≥0.8时,视为两个变量之间高度相关
-
0.5≤|r|<0.8时,视为中度相关
-
0.3≤|r|<0.5时,视为低度相关
-
|r|<0.3时,说明两个变量之间的相关程度极弱,可视为不相关
拟合优度

statsmodels
statsmodels是一个有很多统计模型的python库,能完成很多统计测试,数据探索以及可视化。它也包含一些经典的统计方法,比如贝叶斯方法等。
• 线性模型
• 线性混合效应模型
• 方差分析方法
• 时间序列模型
• 广义矩阵估计方法
三种检验方法
一.t检验(单个参数的显著性检验)
用途:检验单个自变量对因变量是否有显著影响(如"面积是否真的影响房价")。
原假设:H₀: θ_j = 0(第j个自变量的权重为0,即该变量对y无影响)。
步骤:
估计参数θ_j的标准误SE(θ_j)(衡量θ_j的估计精度);
计算t统计量:t = θ_j_hat / SE(θ_j)(θ_j_hat是θ_j的估计值);
对比临界值:若|t| > t_α/2(m-n-1)(m样本量,n自变量数,α显著性水平,如0.05),则拒绝H₀。
核心公式:t = θ_j_hat / SE(θ_j)
二、F检验(整体模型的显著性检验)
用途:检验所有自变量联合起来对因变量是否有显著影响(如"面积+地段+房龄是否共同影响房价")。
原假设:H₀: θ₁=θ₂=...=θ_n=0(所有自变量的权重均为0,模型无意义)。
步骤:
计算总平方和SST = ∑(y_i - ȳ)²(y的总变异)、回归平方和SSR = ∑(ŷ_i - ȳ)²(模型解释的变异)、残差平方和SSE = ∑(y_i - ŷ_i)²(未解释的变异);
计算F统计量:F = (SSR/n) / (SSE/(m-n-1))(n为自变量个数,m-n-1为自由度);
对比临界值:若F > F_α(n, m-n-1),则拒绝H₀。
核心公式:F = (SSR/n) / (SSE/(m-n-1))
三、残差检验(模型假设的诊断检验)
用途:检验模型是否满足误差项的基本假设(正态性、同方差、无自相关),是模型有效的前提。
常用子检验:
正态性:Shapiro-Wilk检验(原假设H₀: 误差项服从正态分布),若p>0.05则不拒绝H₀;
同方差:White检验(原假设H₀: 误差项同方差),若p>0.05则无 heteroscedasticity;
无自相关:Durbin-Watson检验(统计量DW接近2时无自相关,DW<1或>3则存在)。
核心逻辑:通过残差(实际值-预测值)的分布特征,反推误差项是否满足假设,若不满足需修正模型(如加权最小二乘、变量变换)。
F检验(线性关系)
F检验用于判断所有自变量联合起来是否与因变量存在显著线性关系,原假设是所有自变量权重为0(无线性关系),通过对比回归解释的变异与未解释变异的相对大小(F统计量)决定是否拒绝原假设。
T检验(回归系数)
T检验(回归系数)用于判断单个自变量对因变量是否有显著影响,原假设是该自变量的回归系数为0(无影响),通过计算回归系数的t统计量(系数估计值÷标准误)并与临界值比较,决定是否拒绝原假设。
调整R方

简单来说,多元线性回归中直接用R²评估模型会有"虚假提升"问题------不断加变量(哪怕无关),R²也会因总能"多解释点变异"而看似上升,但这其实是过拟合(模型记住了噪声而非规律)。
而调整R²(Adjusted R²)能解决这个问题:它在R²基础上加入"变量数量惩罚"------只有当新变量真的能显著提升模型解释力时,调整R²才会上升;若加的是无关变量(非显著),调整R²反而会下降。因此,多元线性回归中必须用调整R²判断模型效果,避免被"加变量"的虚假拟合迷惑。
数据标准化
0~1标准化:
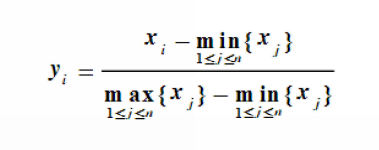
0~1标准化是用公式x_scaled=(x-x_min)/(x_max-x_min)把数据缩放到[0,1]区间的线性变换,能消除量纲影响,但易受极端值干扰。
Z标准化:
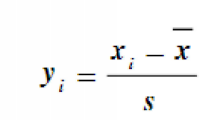
Z标准化是用公式z=(x-μ)/σ将数据转为均值0、标准差1的分布,能消除量纲且对极端值鲁棒,常用于线性回归等需跨特征比较影响的场景。