🎯 开场灵魂拷问:你真的会"找最长递增子序列"吗?
面试官轻描淡写地抛出一句:
"给定一个数组,求它的最长递增子序列长度。"
你以为这是送分题?
结果一写代码才发现------
- 暴力枚举?超时!
- 动态规划?能过但慢如蜗牛!
- 贪心 + 二分?脑子里一团浆糊:"这玩意儿怎么还能用二分?"
别慌,这不是你菜,而是你还没看到这场算法进化的"全貌"。
今天,我们就来拆解 LeetCode 第 300 题 ------ 「最长递增子序列(LIS)」,带你从 暴力直觉 → 动态规划 → 贪心艺术,一步步攀登算法高峰。
✅ 学完你会明白:
- 为什么 DP 是"基础课",而贪心是"研究生选修"?
- 为什么"末尾越小越好"能决定整个序列的命运?
- 以及------二分查找,居然也能用来"维护梦想"?
🧩 第一章:题目解析 ------ 先搞清楚"我们在找什么"
🔍 题目定义(LeetCode 300)
给你一个整数数组 nums,找出其中最长严格递增子序列的长度。
📌 注意关键词:
- 子序列 ≠ 子数组:可以不连续,但必须保持原顺序。
- 严格递增 :
[2,3,3]不算,[2,3,4]才行。 - 只需要返回长度,不要求输出具体序列(除非面试官坏笑说:"那你打印一下?")
🎯 示例:
js
输入: nums = [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长递增子序列为 [2,3,7,18] 或 [2,5,7,101],长度为4。💡 思考起点:
我们不是要"列出所有可能",而是要在 时间与空间的夹缝中,找到最优路径。
🏗️ 方法一:动态规划(DP)------ 暴力中的优雅
⏱️ 时间复杂度:O(n²)
💾 空间复杂度:O(n)
🧠 适合初学者理解本质,也适合面试保底
🤔 核心思想:以我为中心,我能接谁?
我们换个视角思考:
对于每个位置
i,如果我能成为某个递增子序列的"结尾",那这个序列最长能有多长?
于是我们定义状态:
dp[i]= 以nums[i]结尾的最长递增子序列的长度
为什么这样定义?因为:
- 子序列有"延续性":
... → a → b成立的前提是a < b - 所以
dp[i]的值,取决于前面所有比nums[i]小的元素的dp[j]
🔄 状态转移方程
对每个 i,遍历 j ∈ [0, i):
text
if nums[j] < nums[i]:
dp[i] = max(dp[i], dp[j] + 1)初始值:每个元素自己就是一个长度为 1 的子序列 → dp[i] = 1
✅ 代码实现(带注释版)

🧪 执行过程可视化(手把手教学)
以 nums = [10,9,2,5,3,7,101,18] 为例:
| i | nums[i] | 可接的 j | dp[i] 计算过程 | 最终 dp[i] |
|---|---|---|---|---|
| 0 | 10 | - | 初始化为 1 | 1 |
| 1 | 9 | 无 | 无 <9 的前驱 |
1 |
| 2 | 2 | 无 | 同上 | 1 |
| 3 | 5 | j=2 (2<5) | dp[2]+1 = 2 | 2 |
| 4 | 3 | j=2 (2<3) | dp[2]+1 = 2 | 2 |
| 5 | 7 | j=2,3,4 | max(dp[j])+1 = 3 | 3 |
| 6 | 101 | 前面都小 | max(dp[j])+1 = 4 | 4 |
| 7 | 18 | 前面都小 | 但只能接最长链 | 4 |
✅ 最终答案:max(dp) = 4
📉 复杂度分析
- 时间 :O(n²) ------ 双重循环,适合
n ≤ 10³ - 空间 :O(n) ------
dp数组
🟢 优点:逻辑清晰,容易想到,适合面试"先写个能跑的" 🔴 缺点:数据一大就超时,比如 n = 10⁵?直接凉透
🚀 方法二:贪心 + 二分查找 ------ 当算法开始"动脑筋"
⏱️ 时间复杂度:O(n log n)
💾 空间复杂度:O(n)
🧠 适合高手秀操作,也是大厂面试加分项
🤯 关键洞察:我们要的不是"当前最长",而是"未来潜力最大"
动态规划的问题在于:它太"实在"了。
它记录的是"以某点结尾的最长长度",但并不关心"这个序列将来能不能继续增长"。
而贪心策略的核心哲学是:
对于相同长度的递增子序列,末尾越小,未来的路就越宽!
举个例子:
- 序列 A:
[2,5,7],末尾是 7 - 序列 B:
[2,3,7],末尾也是 7,但中间更小
现在来了一个新数字 4:
- A 无法接(7 > 4)
- B 虽然也不能直接接,但如果把
7换成4,就变成了[2,3,4],未来还能接5,6...
所以,我们应该保留那些"末尾尽可能小"的候选序列。
🛠️ 引入神器:tails 数组
我们定义一个辅助数组:
tails[k]= 长度为k+1的递增子序列中,最小的末尾元素
例如:
js
tails = [2, 3, 7, 18]表示:
- 有长度为1的 LIS,最小末尾是 2
- 有长度为2的 LIS,最小末尾是 3
- ...
- 有长度为4的 LIS,最小末尾是 18
🎯 目标:维护这个 tails 数组,让它始终保持"末尾最小化"。
🔁 算法流程:见招拆招
遍历每个 num:
-
如果
num > tails[last]→ 说明它可以扩展当前最长序列!直接追加到末尾。
-
否则(
num <= tails[last])→ 它不能扩展最长序列,但可以"优化"某个较短序列的末尾。
→ 使用二分查找 ,找到第一个
≥ num的位置,把它替换掉。
🧠 替换的意义:我们用
num更新了某个长度的"最佳末尾",让未来更容易扩展。
✅ 代码实现(含详细注释)
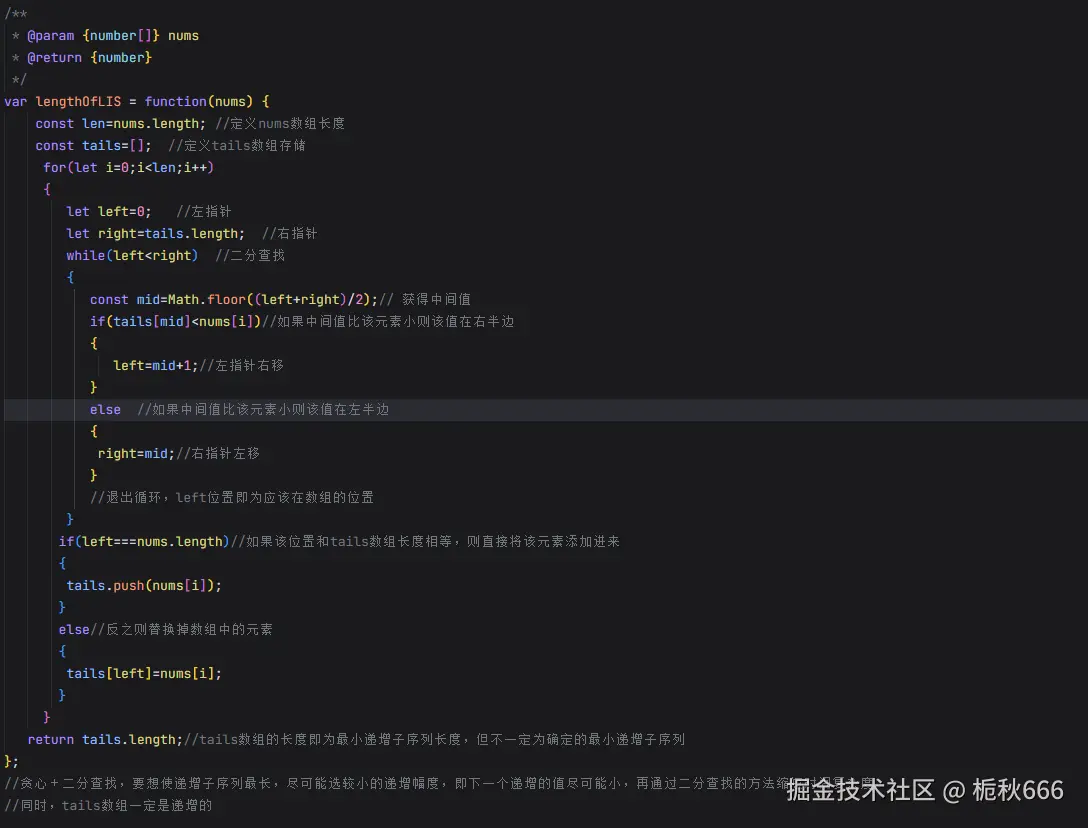
🎬 执行过程动画演示(文字版)
nums = [10,9,2,5,3,7,101,18]
| num | tails 变化 | 说明 |
|---|---|---|
| 10 | [10] |
初始 |
| 9 | [9] |
9 < 10,替换第一个 ≥9 的元素 |
| 2 | [2] |
同上 |
| 5 | [2,5] |
5 > 2,可扩展,追加 |
| 3 | [2,3] |
3 < 5,替换第一个 ≥3 的位置(索引1) |
| 7 | [2,3,7] |
7 > 3,追加 |
| 101 | [2,3,7,101] |
继续追加 |
| 18 | [2,3,7,18] |
18 < 101,替换最后一个 |
✅ 最终长度为 4,正确!
🧠 为什么 tails 是有序的?(关键证明)
很多人疑惑:为什么能用二分查找?
👉 因为 tails 是严格递增的!
反证法:
假设存在 i < j 且 tails[i] >= tails[j]。
那么长度为 j+1 的 LIS 的前 i+1 个元素,构成了一个长度为 i+1 的递增子序列,其末尾 < tails[j] ≤ tails[i],
但这与 tails[i] 是"长度为 i+1 的最小末尾"矛盾!
✅ 所以 tails 必然递增,可用二分!
📉 复杂度分析
- 时间:O(n log n) ------ 每个元素做一次 O(log n) 的二分
- 空间 :O(n) ------
tails最多存 n 个元素
🟢 优势:大规模数据也能轻松应对(n=10⁵ 也没问题) 🔴 劣势:tails 数组并不是真正的 LIS,只是长度正确(想还原序列?得额外记录)
🆚 两种方法对比:一场"稳扎稳打" vs "灵巧突袭"的较量
| 维度 | 动态规划(DP) | 贪心 + 二分 |
|---|---|---|
| 🧠 思维难度 | 简单直观,易理解 | 抽象跳跃,需顿悟 |
| ⏱️ 时间复杂度 | O(n²) | O(n log n) ✅ |
| 💾 空间复杂度 | O(n) | O(n) |
| ✅ 是否稳定 | 是,适合保底 | 是,但难调试 |
| 🖨️ 能否还原子序列 | ✅ 可通过 prev 数组还原 |
❌ tails 不是真实序列 |
| 🎯 适用场景 | 小数据、教学、面试保底 | 大数据、性能敏感、进阶展示 |
💡 高阶技巧与拓展思考
✅ 技巧1:如何还原具体的 LIS?
- DP 方案:额外维护
parent[i]记录前驱节点,最后倒推路径 - 贪心方案:不行(
tails是虚拟状态),但可通过"路径回溯 + 栈"模拟
✅ 技巧2:最长非递减子序列?
只需将条件改为 nums[j] <= nums[i],或在二分查找时找 第一个 > num 的位置进行替换。
✅ 技巧3:结合实际业务?
- 用户行为轨迹中最长"正向成长"路径
- 股票价格中的最长上涨周期
- 文本相似度匹配中的最长公共递增子序列(LCIS)
🧩 面试视角:如果你是面试官,你会怎么问?
- "先说个你能想到的方法。" → 你答 DP,稳妥。
- "有没有更优解?" → 你答贪心 + 二分,加分。
- "为什么
tails可以用二分?" → 你开始讲单调性,面试官点头。 - "那怎么还原具体序列?" → 你微微一笑:"我有备而来。"
🎯 这就是算法面试的"阶梯式挑战":先活下来,再赢下来。
🏁 终极总结:从"复制粘贴"到"创造思维"
| 方法 | 代表能力 | 适合阶段 |
|---|---|---|
| 动态规划 | 基础建模能力 | 初级 → 中级 |
| 贪心 + 二分 | 优化思维 & 数学直觉 | 中级 → 高级 |
🌟 编程的本质,是从"解决问题"到"优雅地解决问题"的进化。
下次当你看到"最长递增子序列",不要再害怕:
- 先写 DP 保命,
- 再秀贪心翻盘,
💬 互动时间
欢迎在评论区留下你的想法:
- 你是怎么第一次理解"贪心 + 二分"这个思路的?
- 你在项目中遇到过类似 LIS 的实际问题吗?
- 你觉得
tails数组像不像"人生梦想清单"?越早把目标调低,未来越容易实现 😂
👇 点赞 + 收藏 + 分享,让更多人告别"只会暴力"的时代!