图像缩放与下采样(Downsampling)
A. 图像缩放的动机
- 图像下采样: 当图像尺寸太大,例如不适合屏幕时,需要创建更小尺寸的版本。
- 图像上采样: 当图像尺寸太小,需要放大到更大的尺寸时。
B. 朴素下采样(Naïve Subsampling)
最简单的下采样方法是:扔掉(跳过)每个多余的行和列 ,从而创建一个 1/21/21/2 或 1/41/41/4 大小的图像。
C. 走样 (Aliasing) 问题
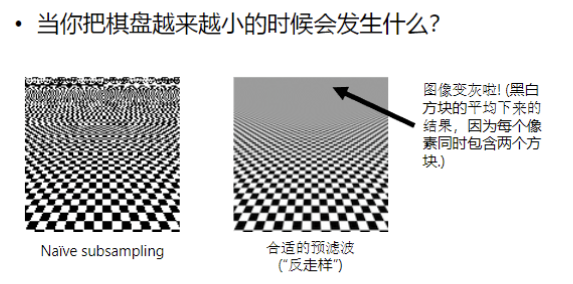
这种朴素的下采样方法会导致严重的图像质量问题,即走样(混叠)。
- 发生原因: 当采样率不足以捕捉图像大量细节的时候就会发生走样。
- 现象: 走样可能给出错误的图像或信号。
- 例如,在棋盘图像上进行朴素下采样,图像会变成灰色,因为每个像素可能同时包含了黑白方块的平均结果。
- 另一个例子是摩尔纹 和著名的车轮效应(在电影中,快速旋转的车轮看起来像在慢慢向后转),。
- 奈奎斯特采样率: 为了防止走样,采样率必须大于或等于图像最高频率的两倍(即每周期两次采样)。
解决方案:高斯预滤波(Gaussian Pre-filtering)
要修复走样问题,尤其是当以下采样 222 的倍数进行时(此时原始图像存在过高的频率),正确的步骤是:
- 解决方案: 先对图像进行滤波(模糊),然后进行下采样,。
- 实现: 这种预滤波通常使用高斯滤波器 (Gaussian)进行,被称为高斯预滤波(Gaussian Pre-filtering)。
- 通过重复进行模糊和 222 倍下采样,可以得到高斯金字塔,。
- 高斯预滤波也被称为反走样 (Anti-aliasing)。
解释:为什么高斯预滤波可以修复走样?
回想一下刚才的奈奎斯特铁律:
采样率 (fsf_sfs) 必须大于 2 倍的信号最高频率 (fmaxf_{max}fmax)。
在下采样(缩小图片)这个场景里:
-
fsf_sfs (采样率) 变低了: 因为你的目标是缩小图片(比如从 1000px 变成 100px),像素格子变稀疏了,你能承载的信息量上限被锁死了。
-
fmaxf_{max}fmax (信号) 依然很高: 原图里那些细密的条纹、锐利的边缘依然存在。
死局出现了: fsf_{s}fs 已经变小了,如果 fmaxf_{max}fmax 还是那么大,就一定会违规(fs<2fmaxf_s < 2f_{max}fs<2fmax),一定会产生摩尔纹(走样)。
解决办法:
既然我们改不了 fsf_sfs(老板非要你缩小图片),那我们只能强行降低 fmaxf_{max}fmax。
-
怎么降低 fmaxf_{max}fmax?就是把原图中那些变化太快、太细微的高频细节抹掉。
-
高斯滤波 就是一个低通滤波器,它像一把剪刀,把超过奈奎斯特极限的高频信号直接剪掉。
结论:
高斯预滤波不是为了"修复"图像,而是为了把那些注定会变成噪音的高频信息,提前杀掉。
上采样
当需要将图像尺寸放大十倍时,最简单的方法是每行和每列重复 101010 次 ,这被称为**"最近邻插值"。然而,为了获得高质量的放大图像,需要进行插值**。
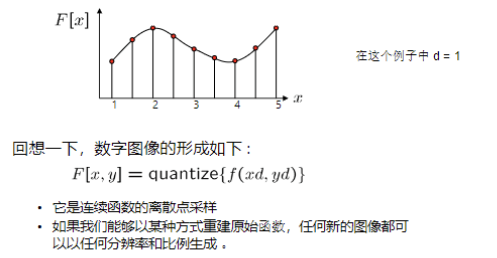
- 理论基础: 数字图像是连续函数 f(x,y)f(x, y)f(x,y) 的离散点采样,。如果我们能以某种方式重建原始函数,那么任何新的图像都可以以任何分辨率和比例生成。
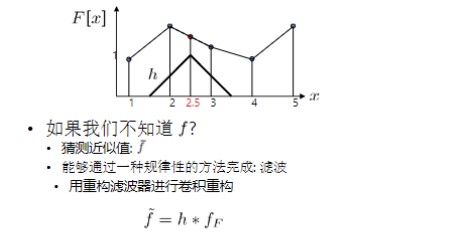
- 实现: 重建过程可以看作是用"重构滤波器"进行卷积。
常见的插值方法
插值方法通过"猜测近似值"来完成,不同的滤波器提供不同的重采样图像,:
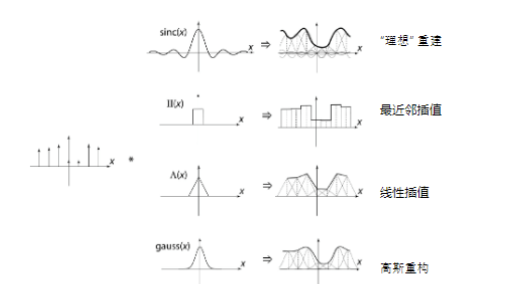
- 最近邻插值 (Nearest Neighbor): 最简单的方法,直接使用最近的像素值,。
-
线性插值 (Linear Interpolation) / 双线性插值 (Bilinear Interpolation) : 线性插值(1D 上的帽子函数 ,即帐篷函数)。
-
双线性插值是线性插值的 2D 版本。
- 双三次插值 (Bicubic Interpolation): 使用三次重构滤波器,是常见的选择,通常能提供更好的重采样图像。
图像插值的几个例子(中间为核函数)
重采样的其他应用
- 多帧图像超分辨率: 如果使用小(亚像素)偏移拍摄多幅场景图像,可以进行更好的上采样。例如,Google Pixel 3 Super Res Zoom 技术就是通过对齐合并多张照片来改善缩放效果。
- 几何形变的实现: 在图像进行反向变形(Inverse Warping)时,由于映射回原图的坐标可能不是整数,也需要采用插值逼近的方法进行近似,以避免正向变形(Forward Warping)中产生的空洞或波纹问题。