WPF Matrix结构体方法ScaleAt的坐标系

代码：

namespace MatrixTransformTest
{
    /// <summary>
    /// MainWindow.xaml 的交互逻辑
    /// </summary>
    public partial class MainWindow : Window
    {
        private MatrixTransform buttonTransform;
        public MainWindow()
        {
            InitializeComponent();
            InitializeButtonTransform();
        }

        private void MyButton_OnClick(object sender, RoutedEventArgs e)
        {

            Debug.WriteLine("=== 点击button1 ===");
            Debug.WriteLine($"缩放前矩阵: {MatrixToString(buttonTransform.Matrix)}");

            Matrix matrix = buttonTransform.Matrix;
            matrix.ScaleAt(1.1, 1.1, 100, 100);

            Debug.WriteLine($"缩放后矩阵: {MatrixToString(matrix)}");
            Debug.WriteLine($"中心点(100,100)变换后: {matrix.Transform(new Point(100, 100))}");

            buttonTransform.Matrix = matrix;
           
        }

        private void InitializeButtonTransform()
        {
            // 创建并初始化MatrixTransform
            buttonTransform = new MatrixTransform();
            myButton.RenderTransform = buttonTransform;

            // 设置初始变换
            ResetTransform();
        }

        private void ResetTransform()
        {
            // 重置为单位矩阵（无变换）
            buttonTransform.Matrix = Matrix.Identity;
        }

       

        

        private void MyButton2_OnClick(object sender, RoutedEventArgs e)
        {
            Debug.WriteLine("=== 点击button2 ===");
            Debug.WriteLine($"缩放前矩阵: {MatrixToString(buttonTransform.Matrix)}");

            Matrix matrix = buttonTransform.Matrix;
            matrix.ScaleAt(1.1, 1.1, 0, 0);

            Debug.WriteLine($"缩放后矩阵: {MatrixToString(matrix)}");

            buttonTransform.Matrix = matrix;
            
        }

        private string MatrixToString(Matrix m)
        {
            return $"[{m.M11:F2},{m.M12:F2},{m.M21:F2},{m.M22:F2},{m.OffsetX:F2},{m.OffsetY:F2}]";
        }
    }
}

xaml:

<Window
    x:Class="MatrixTransformTest.MainWindow"
    xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
    xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
    xmlns:d="http://schemas.microsoft.com/expression/blend/2008"
    xmlns:local="clr-namespace:MatrixTransformTest"
    xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"
    Title="MainWindow"
    Width="800"
    Height="450"
    mc:Ignorable="d">
    <Grid ShowGridLines="True">
        <Grid.RowDefinitions>
            <RowDefinition Height="200" />
            <RowDefinition />
            <RowDefinition />
        </Grid.RowDefinitions>
        <Grid.ColumnDefinitions>
            <ColumnDefinition Width="200" />
            <ColumnDefinition />
            <ColumnDefinition />
        </Grid.ColumnDefinitions>
        <Button
            Name="myButton"
            Grid.Row="0"
            Grid.Column="0"
            Width="100"
            Height="100"
            HorizontalAlignment="Right"
            VerticalAlignment="Bottom"
            Content="Button1"
            Click="MyButton_OnClick" />
        <Button
            Name="myButton2"
            Grid.Row="2"
            Grid.Column="0" 
            Content="Button2"
            Click="MyButton2_OnClick"/>
    </Grid>
</Window>

刚启动的界面：

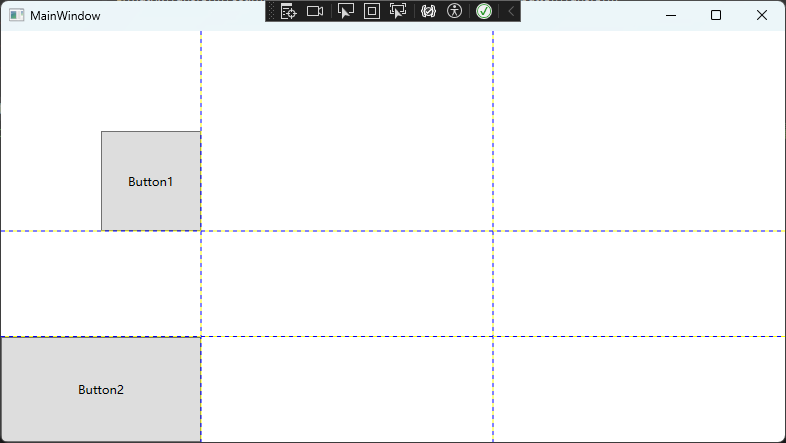
如果一直点击Button1的话，Buttno1的右下角始终与Grid的行列交界重合：

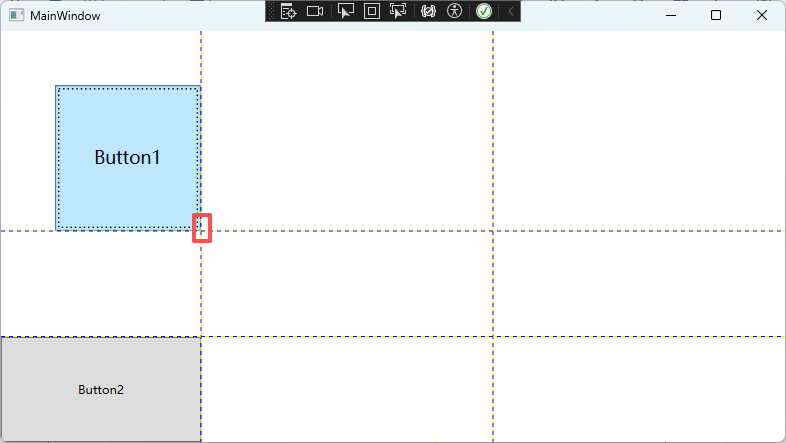
因为Button1的点击事件是以坐标点（100，100）进行缩放，控件的高宽均为100，所以坐标点（100，100）就是Button1的右下角。

同理，如果一直点击Button2的话，Buttno1的左上角位置也不会发生改变：

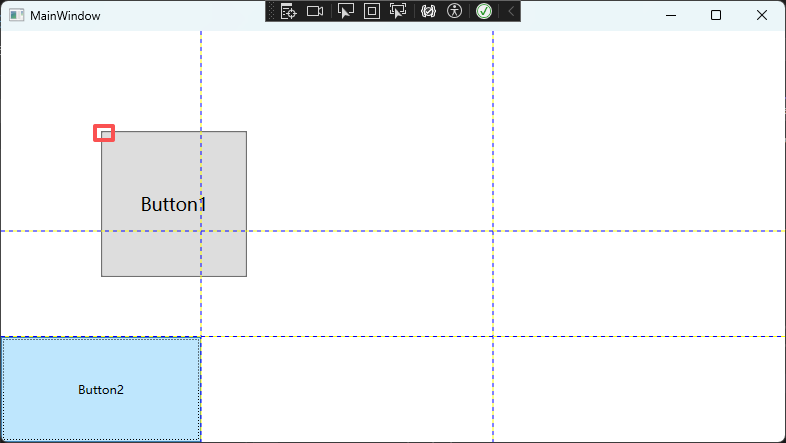
这两种情况实际都符合设想。

同理，Button2点击事件是以（0，0）点为原点进行缩放，所以先点几下按钮1，然后点击按钮2的时候，按钮1的左上角应该不动，视觉上是向右下方进行延申。

但是测试发现我的观点是错误的，实际情况是：先点几下按钮1，然后点击按钮2的时候按钮1的左上角也一直在动。

比如在上图基础上又点了几下按钮2：

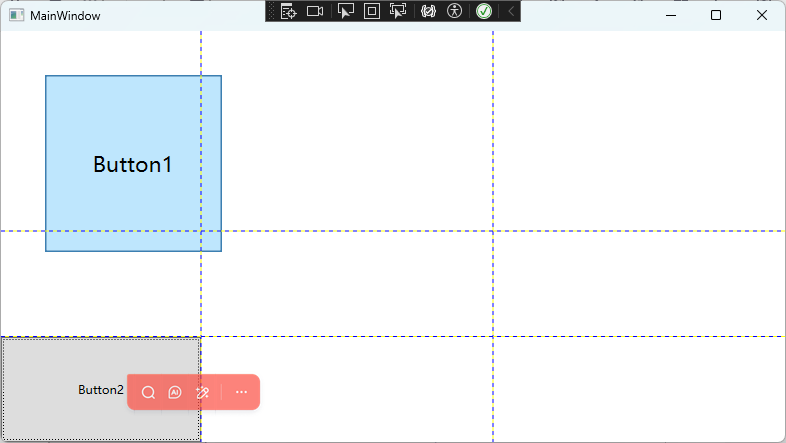
发现按钮1的左上角也一直在偏移，这就说明我对缩放中心的理解是错的。

看一下输出：

先了解一下缩放因子:

图源：深入浅出WPF变换(Transform)之矩阵(Matrix) - 叶落劲秋 - 博客园

问题核心：ScaleAt 的中心点坐标系统

关键事实：

• matrix.ScaleAt(scaleX, scaleY, centerX, centerY) 中的 centerX, centerY 是相对于当前变换后的坐标系统的

• 不是相对于按钮的局部坐标，也不是绝对的窗口坐标

• 每次变换后，整个坐标系都在变化

分析现象

初始状态：

• 按钮在Grid的(0,0)单元格，右下对齐

• 按钮的局部坐标系：左上角(0,0)，右下角(100,100)

• buttonTransform.Matrix = Matrix.Identity（单位矩阵）

场景1：只点击button2

matrix.ScaleAt(1.1, 1.1, 0, 0);

1. 第1次点击：

   • 当前矩阵是单位矩阵 [1,0,0,1,0,0]

   • 以(0,0)为中心放大1.1倍

   • 新矩阵：[1.1,0,0,1.1,0,0]

   • 按钮变大，但位置不变（OffsetX=0, OffsetY=0）

2. 第2次点击：

   • 当前矩阵：[1.1,0,0,1.1,0,0]

   • 还是以(0,0)为中心放大

   • 实际效果：以当前坐标系的原点(0,0) 放大

   • 因为OffsetX和OffsetY一直是0，所以按钮位置不变

场景2：先点击button1，再点击button2

// button1: matrix.ScaleAt(1.1, 1.1, 100, 100);
// button2: matrix.ScaleAt(1.1, 1.1, 0, 0);

1. 第1次点击button1：

   • 以(100,100)为中心放大1.1倍

   • 矩阵从 [1,0,0,1,0,0] 变为 [1.1,0,0,1.1,-10,-10]

   • 为什么Offset变成(-10,-10)？

     • 公式：OffsetX = centerX * (1 - scaleX)

     • 100 * (1 - 1.1) = 100 * (-0.1) = -10

   • 按钮向左上方移动了10像素

2. 第2次点击button2：

   • 当前矩阵：[1.1,0,0,1.1,-10,-10]

   • 以(0,0)为中心放大1.1倍

   • 新的Offset计算：

     • OffsetX' = -10 * 1.1 + 0 * (1 - 1.1) = -11

     • 按钮继续向左移动

   • 每次点击都向左上移动更多

代码与矩阵运算：

关于矩阵的只是可以先参考：https://blog.csdn.net/qq_59062726/article/details/154652614?fromshare=blogdetail&sharetype=blogdetail&sharerId=154652614&sharerefer=PC&sharesource=qq_59062726&sharefrom=from_link

这里分析场景2：先点击button1，再点击button2

先点击按钮1的时候执行：

matrix.ScaleAt(1.1, 1.1, 100, 100);

看一下ScaleAt方法：

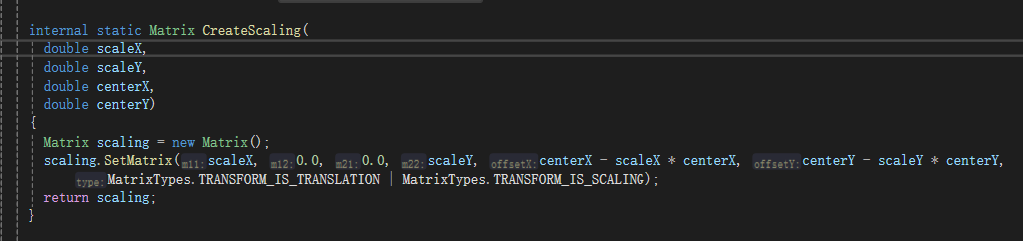
实际上是创造了一个缩放矩阵，然后与当前矩阵相乘；

缩放矩阵的offsetX和offsetY：

offsetX = centerX - scaleX * centerX,

offsetY = centerY - scaleY * centerY

其中scaleX和scaleY是X轴和Y轴上的缩放因子；

所以上方才会说第一次点击按钮1 会导致Offset变成(-10,-10)；

发生的矩阵运算是：

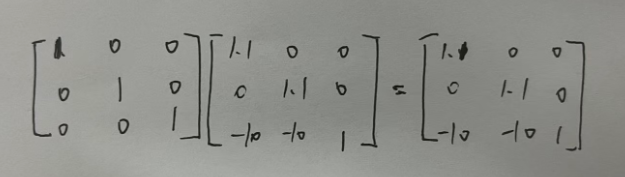
再点击button2的时候执行：

因为以(0,0)为中心放大1.1倍，所以生成的新的缩放矩阵只有scaleX和scaleY有值，且均为1.1。

所以执行的矩阵运算是：

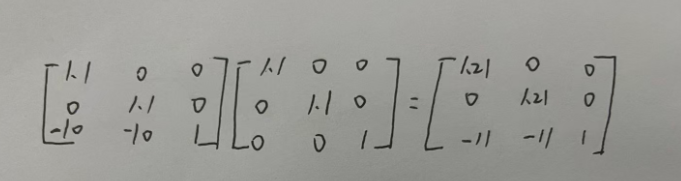
导致原来的-10变为了-11。

扩展：

想要点击按钮2的时候保持按钮1的左上角不动，可以这样修改：

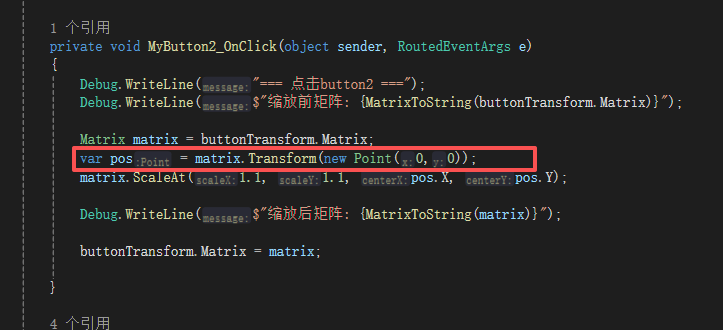
分析一下发生了什么：

1. 初始状态分析

第一次点击button1后：

matrix = [1.1, 0, 0, 1.1, -10, -10]

此时，局部坐标(0,0)经过变换后：

var pos = matrix.Transform(new Point(0, 0));
// pos.X = 1.1*0 + 0*0 + (-10) = -10
// pos.Y = 0*0 + 1.1*0 + (-10) = -10
// pos = (-10, -10)

2. 方法执行过程

matrix.ScaleAt(1.1, 1.1, pos.X, pos.Y);
// 等价于：
matrix.ScaleAt(1.1, 1.1, -10, -10);

创建缩放矩阵：

S = [1.1, 0, 0, 1.1, 
     centerX*(1-1.1), centerY*(1-1.1)]
  = [1.1, 0, 0, 1.1,
     (-10)*(1-1.1), (-10)*(1-1.1)]
  = [1.1, 0, 0, 1.1,
     (-10)*(-0.1), (-10)*(-0.1)]
  = [1.1, 0, 0, 1.1, 1, 1]

3. 矩阵乘法计算

当前矩阵：M = [1.1, 0, 0, 1.1, -10, -10]

缩放矩阵：S = [1.1, 0, 0, 1.1, 1, 1]

text

新矩阵 = S × M = [
  // 左上2x2部分
  1.1*1.1 + 0*0 = 1.21,
  1.1*0 + 0*1.1 = 0,
  0*1.1 + 1.1*0 = 0,
  0*0 + 1.1*1.1 = 1.21,
  
  // OffsetX: 1.1*(-10) + 0*(-10) + 1 =  -10
  // OffsetY: 0*(-10) + 1.1*(-10) + 1 =  -10
]

结果：

新矩阵 = [1.21, 0, 0, 1.21, -10, -10]

与点击按钮2之前的矩阵的偏移一致。

理解：

var pos = matrix.Transform(new Point(0, 0))就是得到了在当前矩阵下的（0，0）坐标，也就是视觉上的（0，0）点，对于当前矩阵来说实际上是pos， 然后以pos为中心进行缩放，pos点的位置不变。